基于PFC的先锋闸站移建工程中黏土堆筑料三轴力学特性影响因素研究

陆 昊，朱小磊，石超磊

(1.常州市长江堤防工程管理处，江苏 常州 213000； 2.常州市城市防洪工程管理处，江苏 常州 213000； 3.常州市河道湖泊管理处，江苏 常州 213000)

水利工程中岩土体材料的力学特性对工程设计具有重要价值，因而许多水利工程师开展过关于岩土类材料力学特征的探讨，从而推动水利设计发展[1-3]。韩雪等[4]、杨芊等[5]、平永庆等[6]通过类比岩石类材料设计室内单、单轴试验，研究了土体等水利材料力学特征，并开展相关影响性分析，为认知土体材料力学水平提供依据。与室内试验形成鲜明对比的是，在现场利用微震，或在室内利用电镜、CT等细观研究手段，可探知土体微观上力学特征变化，进而为土体宏观上力学解探讨提供支撑[7-9]。不可忽视，数值仿真手段应用较为广泛，作为颗粒类组成材料，以颗粒流离散元仿真手段，可高效解决黏土类材料力学特征求解，为认识土体材料力学特征以及其影响参数提供快捷高效的手段，目前在王瑶等[10]、潘远阳等[11]、李远征等[12]研究中已得到体现。本文基于先锋闸站移建工程围堰设施黏土体堆筑料的背景，以PFC仿真计算系统为研究手段，设计不同因素的试验方案，为了解黏土这类材料三轴力学特性影响因素提供重要参考。

1 试验概况

1.1 工程背景

先锋闸站乃是钟楼区重要水利枢纽设施，其安全可靠性对提升区域用水安全以及防洪安全均具有重要作用，但现由于闸站设计运营年限较长，部分水利设施老化严重，闸室安全性受到巨大挑战，管理部门考虑对闸站开展移建工程设计，继续使闸站工程成为区域内重要的水利设施，在地区防洪、蓄水、引水及提升水质等重大领域承担关键作用。目前由于闸站移建工程中所涉及到的节制闸以及抽水泵站施工，均需确保上、下游水位不应处于过高状态，因而设置临时挡水设施很有必要，故工程设计部门考虑增设围堰设施，确保闸站移建工程安全高效进行。根据现场地质勘探，围堰所需堆筑料以砂土以及黏土为主，其中黏土料占分层堆筑总量的60%，在与围堰设施钢管桩相互协调过程中，黏土承载能力稳定性极大影响了分层堆筑效果，若黏土体发生失稳滑移，对围堰整体安全稳定性乃是重大威胁。因而，工程设计部门考虑对黏土体基本力学特征开展研究，并专注于黏土体三轴力学特征，进而为黏土体分层堆筑设计提供重要力学数据参考，为确保工程设计效率，本文主要利用颗粒流PFC仿真计算平台开展黏土体三轴力学特征仿真试验计算。

1.2 试验方案

颗粒流PFC分析软件乃是研究颗粒组成物类材料力学变化的仿真计算平台，可根据闸站移建工程所处施工环境以及荷载变化条件，利用PFC可设定相关约束状态，进而仿真计算出土体实际应力变形变化特征。另一方面，为确保黏土三轴力学仿真计算准确性，本文选取线性接触黏结本构模型作为组成黏土体的颗粒物基本力学方程，其几何示意图如图1所示，两个方向的刚度系数服从式(1)～式(2)[13-14]：

(1)

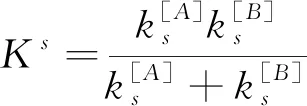
(2)

图1 颗粒线性接触本构模型示意图

在PFC 3D中颗粒运动服从旋转运动与合力矩方程，其具体表达如式(3)～式(4)：

(3)

(4)

基于上述颗粒运动方程以及物理参数条件，设定不同的边界条件，求解计算出黏土颗粒流模型中每个颗粒的力学特征参数，进而在PFC软件中耦合计算出黏土在不同外荷载约束条件下的力学特征变化，本文以此为原理开展三轴力学特征计算。根据闸站移建工程实际状态，设置试验围压为100 kPa、200 kPa、300 kPa、400 kPa，颗粒体半径设定为0.1 mm，按照工程现场所测出的黏土孔隙率为12%，因而仿真计算平台中确保颗粒体所组成的砂土孔隙率为15%。按照黏土影响因素划分，本文从黏土自身刚度参数以及颗粒力学特征参数两方面开展分析，其中刚度参数以刚度比作为衡量指标，分别设定为0.4、0.8、1.2、1.6、2.0，而颗粒力学特征参数分别为弹性模量与内摩擦角，其中弹性模量设定为1.0 MPa、1.5 MPa、2.0 MPa、2.5 MPa、3.0 MPa，内摩擦角分别设定为10°、20°、30°、40°、50°，三轴力学特征影响性分析组中各黏土体颗粒参数除单一对比因素有所差异外，其余物理参数或颗粒形状均为一致。各组具体围压以及其他试验条件如表1试验方案所示。

黏土体三轴力学试验计算过程如下：

(1)按照既定颗粒属性以及试验参数要求随机生成1000粒圆形颗粒，颗粒间为线性黏结接触，此1000粒颗粒组成直径、高度分别为60 mm、20 mm的黏土体试样，图2为所生成的黏土体离散元模型；

(2)按照三轴力学试验边界约束荷载要求，控制荷载约束条件，在黏土体模型四周施加围压约束条件，待达到目标试验围压值后，开始按照变形速率0.001 mm/s递进式施加两端部轴向约束荷载，直至黏土体模型出现承载力衰退并失稳破坏；

表1 试验方案

图2 黏土体离散元模型

(3)停止轴向荷载约束条件的递增，结束仿真试验，导出PFC所计算出的黏土体三轴全过程力学特征数据，后重复进行其他试验组仿真试验。

2 刚度对黏土体三轴力学特性影响

采用PFC仿真系统计算后获得刚度参数对黏土三轴力学特性影响特性，如图3所示。从图中可看出，各刚度比试样应力应变曲线走向基本一致，各变形阶段基本同步，其中以刚度比为2的试样线弹性模量为最大，达97.6 kPa，乃是刚度比0.4、0.8、1.2、1.6各个试样弹性模量的1.30倍、1.24倍、1.19倍、1.08倍，各试样间幅度差异较小，即刚度对黏土试样的影响还较有限。另一方面从变形来看，各刚度比试样峰值应力点应变基本均为一致，均稳定在5.6%，且黏土试样进入屈服变形阶段加载应力点对应的应变亦基本一致，为1.5%，表明刚度对黏土变形无影响。笔者认为，刚度参数一定程度上反映了岩土材料抵抗弹性变形的一种能力，而对于黏土试样来说，其弹性变形量较小，改变刚度参数对黏土三轴力学特征影响微著。再者从屈服变形阶段加载应力特征可看出，刚度比与加载应力为正相关关系，当应变为2%时，刚度比0.4试样的加载应力为132.5 kPa，而刚度比0.8、1.2、1.6、2.0的试样相对应的加载应力相比前者分别增大了10.0%、14.3%、22.5%、31.5%，特别是在峰值应力点附近，刚度影响各试样加载应力关系显著；当进入残余应力阶段，各试样残余应力基本保持一致，无显著性差别，各试样残余应力稳定在136.5 kPa；由此表明，刚度比对于黏土体承载能力具有一定影响，但仅限于峰值应力附近。

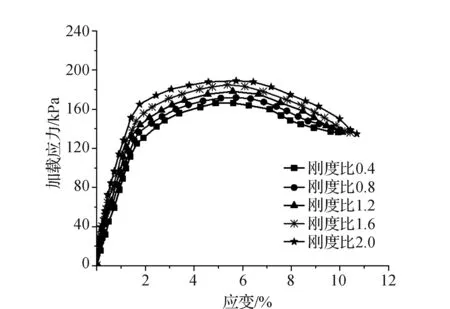
图3 不同刚度比黏土三轴应力应变曲线

图4为不同围压下刚度比与黏土三轴抗压强度、残余强度关系曲线。从图中可看出，抗压强度与刚度比参数具有线性增长关系，增长斜率较小为14.7，平均刚度比每增长0.4，三轴抗压强度增长3.2%，当围压增大至400 kPa时，三轴抗压强度整体水平均有增长，但各刚度比试样间幅度差异并无显著性增长，仍控制在刚度比增长0.4，抗压强度增长约3.5%。残余强度在各刚度比下均保持不变，围压增大至400 kPa后，残余强度仍保持不变，相比围压200 kPa下，增长了约21.2%。综上表明，围压并不改变刚度比对黏土试样力学特征影响。

3 颗粒力学特征参数对黏土体三轴力学特性影响

3.1 弹性模量

由于PFC仿真计算中主要以颗粒运动特征入手，进而计算出黏土试样的力学特征，因而颗粒力学特征参数对黏土试样具有重要影响，本文颗粒力学特征参数主要选取弹性模量与内摩擦角作为典型分析，图5为颗粒弹性模量影响下黏土试样三轴应力应变曲线。

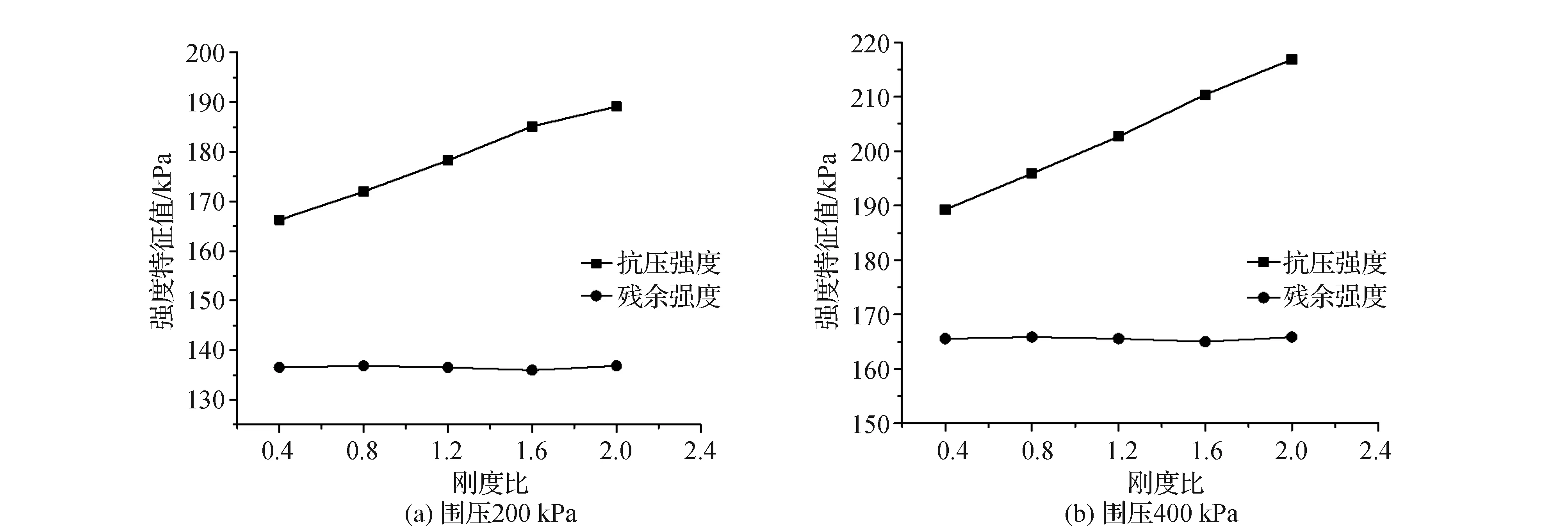
图4 强度特征值与刚度参数关系

从图5可知，颗粒弹性模量与加载应力为正相关，在相同应变2%时，弹性模量1 MPa试样对应的加载应力为55.6 kPa，而弹性模量增大至2 MPa、7 MPa后，相对应的加载应力乃是前者的1.98倍、3.40倍；从线弹性变形阶段可看出，当弹性模量愈大，则黏土试样线弹性变形增长斜率愈高，进而呈现出较大的脆性破坏特征，其峰值应力后具有显著应力下降段，弹性模量7 MPa试样峰值应力后下降幅度最大可达38.9%，而弹性模量1 MPa试样峰值应力后下降幅度较小，仅为13.5%，表明弹性模量可促进黏土试样承载能力增长，但同时也加大了黏土试样脆性破坏特征。从峰值应力点应变可知，弹性模量1 MPa、2 MPa、7 MPa试样对应的应变分别为5.7%、5.2%、3.6%，弹性模量愈大，愈导致试样峰值应力前以弹性变形为主，塑性变形占比较小。

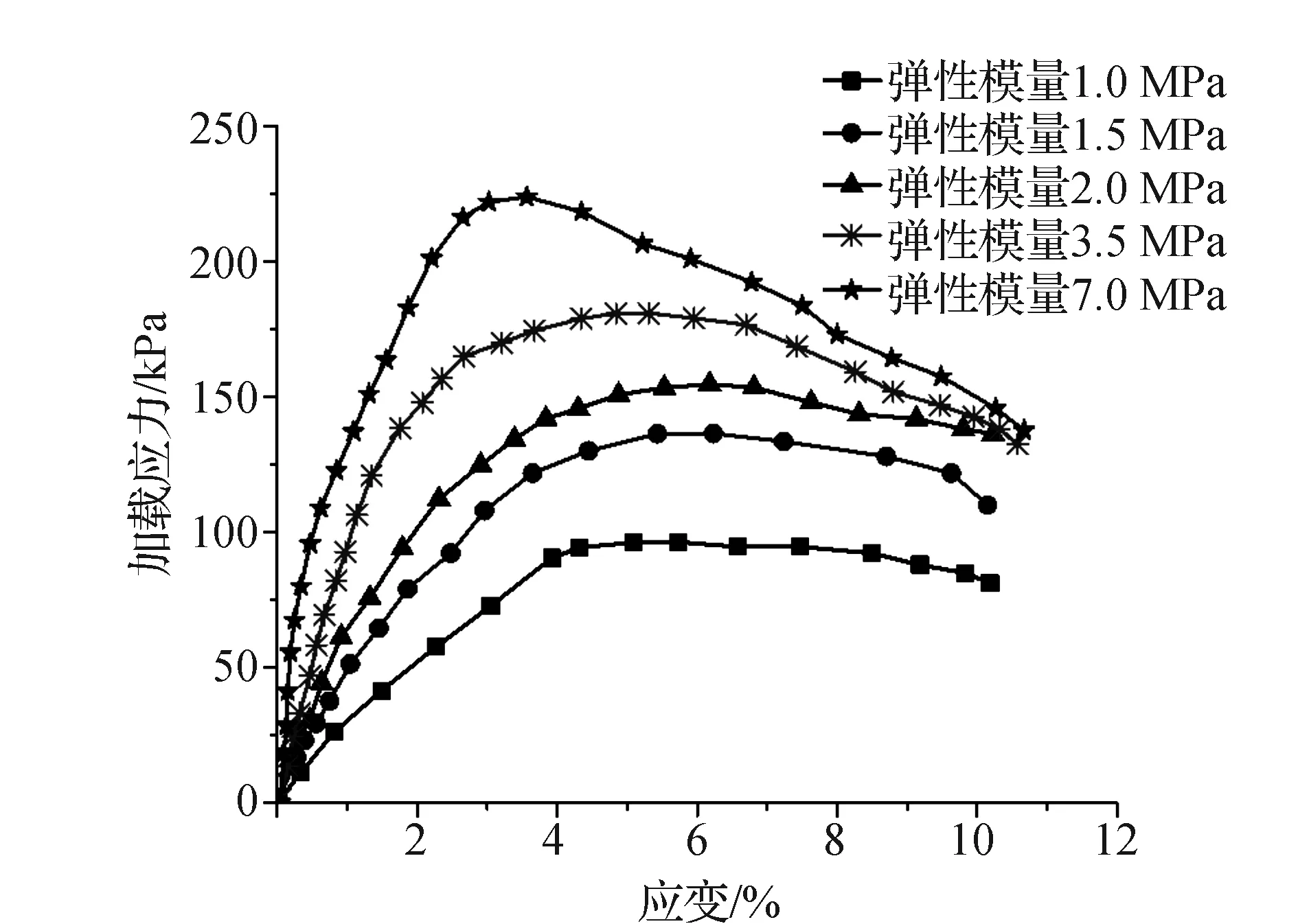
图5 不同颗粒弹性模量黏土三轴应力应变曲线

图6为强度特征参数与颗粒弹性模量之间关系。从图中可知，三轴抗压强度与颗粒弹性模量具有对数函数关系，颗粒弹性模量为1.0 MPa的试样抗压强度为96.5 kPa，而颗粒弹性模量为1.5 MPa、3.5 MPa、7.0 MPa试样抗压强度相比前者分别增大了41.5%、87.6%、132.2%，颗粒弹性模量E与三轴抗压强度F之间函数关系可表述为公式(5)

F=62.4lnE+105

(5)

当围压增大，颗粒弹性模量与三轴抗压强度亦为对数函数关系，且各颗粒弹性模量试样的抗压强度幅度差异并无显著差别。残余应力随颗粒弹性模量递增，在围压200 kPa时，颗粒弹性模量2 MPa时的残余强度为126.4 kPa，当围压增大至400 kPa，相同颗粒弹性模量下的残余强度相比前者增大了26.2%。

3.2 内摩擦角

同理类似，计算获得内摩擦角对黏土试样三轴应力影响特性，如图7所示。从图7可看出，内摩擦角在加载应力125 kPa后对黏土试样力学特征具有显著影响，相同加载应变3.5%时，内摩擦角10°试样的加载应力为150.1 kPa，而加载应力为40°、80°试样相对应的加载应力乃为前者的19.9%、46.7%；从变形特征可看出，内摩擦角10°、20°、40°、60°试样峰值应力点对应的应变分别为4.9%、6.1%、6.6%、7.2%，即内摩擦角具有促进峰值应力点应变增长效应；分析认为，内摩擦角反映了黏土试样内摩各颗粒间彼此咬合以及黏结的一种程度，当内摩擦角愈大，表明黏土颗粒互相连接紧密，咬合度较高，彼此具有较强的整体协调性，颗粒骨架完整性与胶结性较好，可承受较大的荷载约束，因而三轴加载应力较高，且变形能力较强。从峰值应力后阶段可看出，内摩擦角愈大的黏土试样应力下降幅度愈显著，其中内摩擦角80°试样峰值应力后应力下降幅度达36.7%，而内摩擦角10°、20°试样应力下降幅度仅为13.3%、15.6%，表明内摩擦角增大，促进了黏土试样的脆性变形。

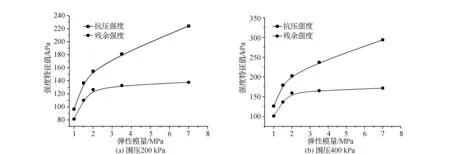
图6 强度特征值与颗粒弹性模量关系

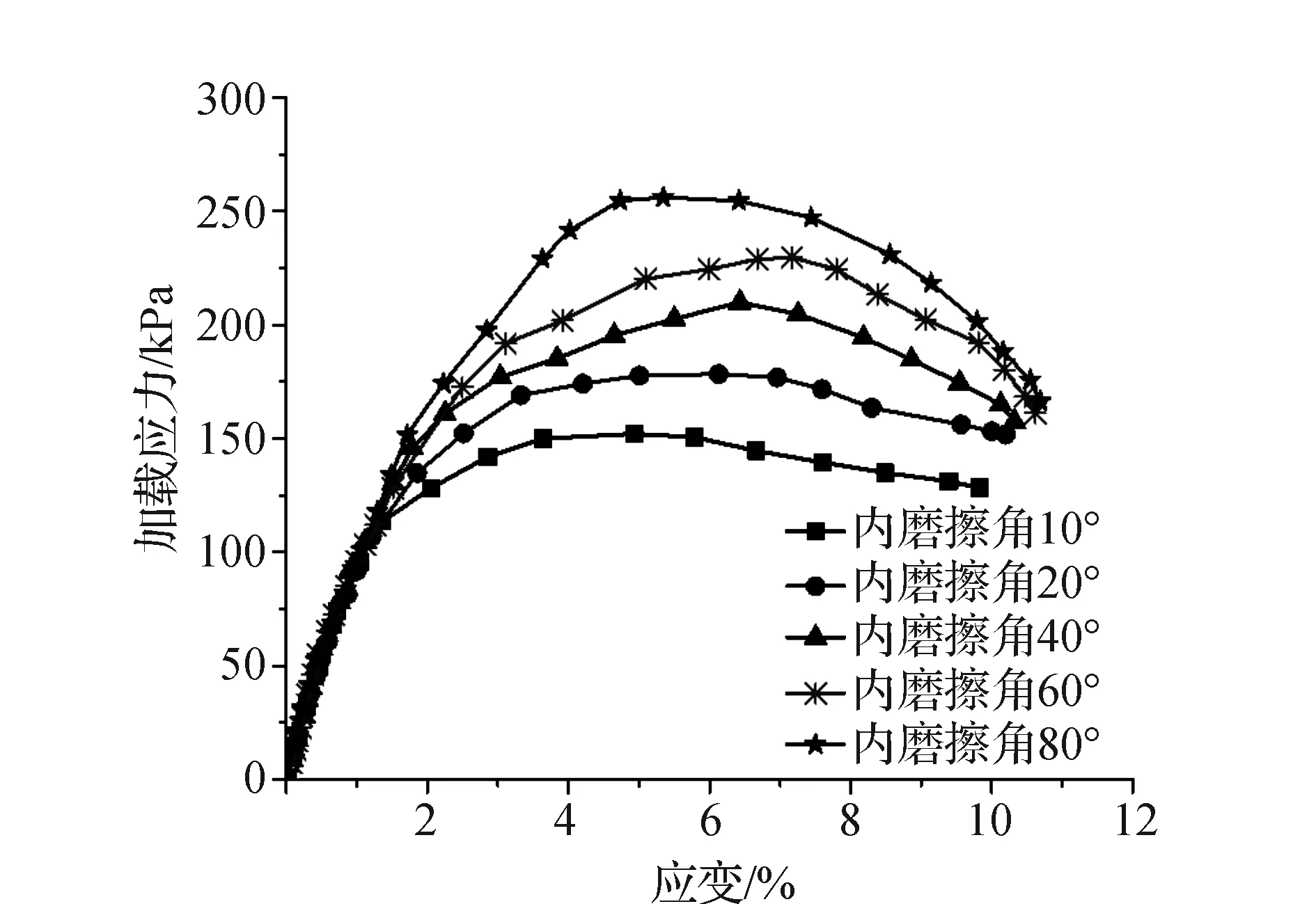
图7 不同颗粒内摩擦角黏土三轴应力应变曲线

图8为强度特征参数与内摩擦角关系曲线。从图中曲线变化可知，三轴抗压强度与内摩擦角亦具有对数函数关系，内摩擦角10°试样抗压强度为152.1 kPa，而内摩擦角40°、80°试样抗压强度相比前者分别增大了38.0%、68.4%。从残余强度变化可知，内摩擦角可促进残余强度增长，内摩擦角80°试样的残余强度达175.9 kPa，而内摩擦角为10°时试样的残余强度仅为前者的70%。

图8 强度特征值与颗粒内摩擦角关系

4 结 论

本文主要有如下结论：

(1)刚度对黏土试样力学特征影响有限，在屈服塑性变形阶段，与黏土试样为正相关，但增长幅度较小，平均刚度比每增长0.4，抗压强度增长3.2%，围压增大，并影响抗压强度增长幅度，刚度参数对残余强度无影响，相同围压下各刚度比试样残余强度保持一致，其中围压400 kPa残余强度相比围压200 kPa下增长了21.2%。

(2)弹性模量愈大，黏土脆性变形特征愈显著，峰值应力后具有显著应力下降段，弹性模量7 MPa试样峰值应力后下降幅度最大可达38.9%；三轴抗压强度与颗粒弹性模量具有对数函数关系，围压增大，两者亦保持为对数函数关系，残余强度随颗粒弹性模量变化递增。

(3)内摩擦角在加载应力125 kPa后对黏土试样力学特征影响显著，内摩擦角愈大，试样变形能力愈强，亦增强了脆性变形特征，且残余强度得到增长；三轴抗压强度与内摩擦角亦具有对数函数关系，内摩擦角40°、80°试样抗压强度相比内摩擦角10°试样分别增大了38.0%、68.4%。