Hesitant Fuzzy Filters of Heyting Algebras

PENG Jiayin

(School of Mathematics and Information Science, Neijiang Normal University, Neijiang, Sichuan 641100, China)

Abstract: Application of hesitant fuzzy sets to filter theory of Heyting algebras is discussed. The notion of hesitant fuzzy (Boolean,implicative, positive implicative, ultra, obstinate ) filter of Heyting algebras is introduced, and related properties are investigated. Characterizations of hesitant fuzzy (Boolean,implicative, positive implicative, ultra, obstinate ) filters of Heyting algebras are derived. Conditions for a hesitant fuzzy set to be a hesitant fuzzy filter are investigated. the equivalent relation between a hesitant fuzzy (Boolean) filter and a hesitant fuzzy (implicative) positive implicative filter is given. The extension properties for hesitant fuzzy Boolean filter, hesitant fuzzy ultra filter and hesitant fuzzy obstinate filter are established. Finally, it is proved that the homomorphic preimage of a hesitant fuzzy (Boolean,implicative, positive implicative, ultra, obstinate ) filter is also a hesitant fuzzy (Boolean,implicative, positive implicative, ultra, obstinate ) filter.

Keywords: heyting algebra; hesitant fuzzy set; hesitant fuzzy (Boolean, implicative, positive implicative, ultra, obstinate) filter

1 Introduction

As it is know, an important task of the artificial intelligence is to make the computers simulate human being in dealing with certainty and uncertainty in information. Logic give a technique for laying the foundations of this task. The processing of certain information is based on the classical two-valued logic, nonclassical logic including logics behind fuzzy reasoning handle information with various facets of uncertainty[1]such as fuzziness, randomness, vagueness,and so on. Therefore, nonclassical logic has become a formal and useful tool for computer science to deal with uncertain information.

The classical two-valued logic has Boolean algebras as an algebraic semantics. Similarly, for important nonclassical logics there are algebraic semantics in form of classes of algebras. Using these classes, one can get an algebraization of inference systems that handle various kinds of uncertainty. Heyting algebra is introduced as algebraic sematics of intuitionistic propositional logic such that the law of excluded middle on logic rules does not generally hold, and also an important algebraic model of lattice theory. The algebraic properties, structure and topological characteristics of Heyting algebras have been discussed in the[2-9]. In logical algebras, filter is one of the most powerful tool to study the algebraic structure. Filters based on a variety of different forms of logical algebra are proposed, and a lot of research results in theoretical value and application prospects are obtained[10-13]. Gierz et al.[14]defined the filters in Heyting algebras by using the languages of lattice theory and logics, respectively, and pointed out that the two definitions are equivalent.

Nowadays, even if Zadeh’s fuzzy set theory[15]and its modified versions, such as interval-valued fuzzy sets[16], vague sets[17], intuitionistic fuzzy sets[18], type 2 fuzzy sets[19], bipolar-valued fuzzy set[20], ect., are a newly emerging class of mathematical tools to handle uncertainty, they are not appropriate to deal with the situations in which the difficulty of establishing the membership degree is not due to the margin of error or some possibility distribution of the possible values, but due to our hesitation between a few different values. So, in order to accurately and perfectly describe the decision maker’s opinions in the real decision making problems, Torra[21]proposed recently a concept of hesitant fuzzy sets to permit the membership degree of an element to a set to be represented by a set of possible values between 0 and 1. Therefore, the hesitant fuzzy set is a very useful too to deal with uncertainty, and bas been applied to several practical problems, primarily in the area of decision making[22-29].

The study of the fuzzy algebraic structures has started with the introduction of the concepts fuzzy (subgroupoids) subgroups and fuzzy (left, right) ideals in the pioneering paper of Rosenfeld[30]. Up to now, many theories dealing with uncertainty has been applied to many algebraic structures. Recently, several researchers has applied the hesitant fuzzy set theory to some algebraic structures, such as semigroup[31], residuated lattice[32], BCK-algebra[33], MTL-algebra[34], and so on. In this paper, we will apply the hesitant fuzzy set to Heyting algebra, especially filter theory of Heyting algebras, introduce the concepts of hesitant fuzzy (Boolean, implicative, positive implicative, ultra, obstinate) filters of Heyting algebras, and investigate several properties including the homomorphic preimages of these hesitant fuzzy filters. We discuss the relations among these hesitant fuzzy filters, and conditions for a hesitant fuzzy set to be a hesitant fuzzy filter. We give the extension theorems of hesitant fuzzy Boolean filters, hesitant fuzzy ultra filters and hesitant fuzzy obstinate filters.

2 Preliminaries

Definition 2.1[3-4]A latticeLis said to be a Heyting algebra if there exists a binary operation→:L×L→Lsuch thatc≤a→b⟺c∧a≤bfor anya,b,c∈L.

Each Heyting algebra is a distributive lattice with maximum element 1[3-4].

Theorem 2.1[3-4]LetLbe a Heyting algebra with maximum element 1. Then the following hold for allx,y,z∈L:

(1)x→x=x→ 1 = 1;

(2) 1 →x=x;

(3)x→y= 1 ⟺x≤y;

(4)x→ (y→z) =y→ (x→z) = (x∧y) →z;

(5)x→ (y∧z) = (x→y) ∧ (x→z);

(6) (x∨y) →z= (x→z) ∧ (y→z);

(7) ((x→y) →y) →y=x→y;

(8)x∧ (x→y) =x∧y;

(9)x≤ (x→y) →y.

Definition 2.2[14]LetLbe a Heyting algebra and ∅≠H⊆L. A setHis called a filter ofLif it satisfies

(H1) 1 ∈Hfor allx∈L;

(H2)x∈Handx→y∈Himplyy∈Hfor allx,y∈L.

LetLbe a Heyting algebra, denotex-=x→ 0. We present now several notions on filter theory of Heyting algebras[5]as follows:

A filterHof a Heyting algebraLis called a Boolean filter ofLifx∨x-∈Hfor anyx∈L. A filterHof a Heyting algebraLis said to be implicative ifx→ (z-→y) ∈Handy→z∈Himplyx→z∈Hfor allx,y,zinL. A filterHof a Heyting algebraLis said to be positive implicative ifx→ (y→z) ∈Handx→y∈Himplyx→z∈Hfor allx,y,z∈L. A filterHof a Heyting algebraLis said to be ultra ifx∈Horx-∈Hfor allx∈L. A filterHof a Heyting algebraLis said to be obstinate ifxHandyHimplyx→y∈Hfor allx,y∈L.

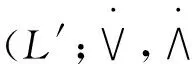
It is clear that iff:L→L′ is a homomorphism, thenf(1) = 1′.

Definition 2.4[21]LetXbe a reference set. A hesitant fuzzy setFonXis defined in terms of a functionhF(x) that returns a subset of [0,1] when it is applied toX, i.e.,F= {〈x,hF(x)〉|x∈X} wherehF(x) is a set of some different values in [0,1], representing the possible membership degrees of the elementx∈XtoF.

3 Hesitant fuzzy filters of Heyting algebras

Definition 3.1LetLbe a Heyting algebra, a hesitant fuzzy setFonLis called a hesitant fuzzy filter ofLif it satisfies:

(F1)hF(1) ⊇hF(x) for anyx∈L;

(F2)hF(x→y) ∩hF(x) ⊆hF(y) for anyx,y∈L.

Theorem 3.1LetLbe a Heyting algebra andFa hesitant fuzzy set ofL. ThenFis a hesitant fuzzy filter ofLif and only if the setFτ:= {x∈L|τ⊆hF(x)} is a filter ofLfor anyτ∈P([0,1]) withFτ= ∅.

ProofSuppose thatFis a hesitant fuzzy filter ofLandx,y∈L,τ∈P([0,1]) be such thatx→y∈Fτandx∈Fτ. Thenτ⊆hF(x→y) andτ⊆hF(x). It follows thathF(1) ⊇hF(x) ⊇ τ andhF(y) ⊇hF(x→y) ∩hF(x) ⊇ τ ∩ τ = τ, and so 1 ∈Fτandy∈Fτ. Therefore,Fτis a filter ofL.

Conversely, assume thatFτis a filter ofLfor anyτ∈P([0,1]) withFτ≠ ∅. For anyx,y∈L, lethF(x)=t, sinceFτis a filter ofL, we have 1 ∈Ft, and sohF(1) ⊇t=hF(x). Now, lethF(x→y) = s. Obviously,x∈Ft∩sandx→y∈Ft∩swhich implyy∈Ft∩s. Therefore,hF(y) ⊇t∩s=hF(x)∩hF(x→y), and henceFis a hesitant fuzzy filter ofL.

Corollary 3.1LetLbe a Heyting algebra andFa hesitant fuzzy filter ofL. Then the set Ωa:= {x∈L|hF(a) ⊆hF(x)} is a filter ofLfor anya∈L, wherehF(a) = ∅.

Nothing daunted5, however, he went on and on, till he perceived that he was entering a valley with great rocky mountains on all sides, and that his horse was getting very tired and trembled at every stride

ProofSincehF(1) ⊇hF(a) for alla∈L, we have 1 ∈ Ωa. Letx,y∈Lbe such thatx∈ Ωaandx→y∈ Ωa. ThenhF(x) ⊇hF(a) andhF(x→y) ⊇hF(a). SinceFa hesitant fuzzy filter ofL, it follows from (F2) thathF(y) ⊇hF(x) ∩hF(x→y) ⊇hF(a) so thaty∈ Ωa. Hence Ωais a filter ofL.

Theorem 3.2LetLbe a Heyting algebra andFa hesitant fuzzy set ofL. ThenFis a hesitant fuzzy filter ofLif and only if, for anyx,y,z∈L,x→ (y→z) = 1 implieshF(z) ⊇hF(x)∩hF(y).

ProofSuppose thatFis a hesitant fuzzy filter ofL, andx→ (y→z) = 1. By (F2) and (F1), we havehF(y→z) ⊇hF(x) ∩hF(x→ (y→z)) =hF(x) ∩hF(1) =hF(x). SohF(z) ⊇hF(y) ∩hF(y→z) ⊇hF(y) ∩hF(x) for allx,y,z∈L.

Conversely, assume thatx→ (y→z) = 1 implieshF(z) ⊇hF(x) ∩hF(y) for allx,y,z∈L. By Theorem 2.1(1), we getx→ (x→ 1) = 1, and sohF(1) ⊇hF(x) ∩hF(x)=hF(x) for allx∈L. By Theorem 2.1(9) and Theorem 2.1(3),x→ ((x→y) →y) = 1. It follows thathF(y) ⊇hF(x)∩hF(x→y) for allx,y∈L. Therefore,Fa hesitant fuzzy filter ofL.

Corollary 3.2LetLbe a Heyting algebra andFa hesitant fuzzy set ofL. ThenFis a hesitant fuzzy filter ofLif and only if, for anyx,y,z∈L,x∧y≤zimplieshF(z) ⊇hF(x) ∩hF(y).

ProofBy Definition 2.1 and Theorem 2.1(3),x∧y≤zif and only ifx→ (y→z) = 1. From Theorem 3.2, we can complete the proof.

Theorem 3.3A hesitant fuzzy setFof Heyting algebraLis a hesitant fuzzy filter ofLif and only if, for anyx,y∈L,

(F3)x≥yimplieshF(x)⊇hF(y);

(F4)hF(x∧y) ⊇hF(x) ∩hF(y).

ProofSuppose thatFis a hesitant fuzzy filter ofL, andx≥y. Theny→x= 1 by Theorem 2.1(3), it follows from (F2) and (F1) thathF(x) ⊇hF(y) ∩hF(y→x) =hF(y) ∩hF(1) =hF(y). Sincex∧y≤x∧yfor allx,y∈L, we havehF(x∧y) ⊇hF(x) ∩hF(y) by Corollary 3.2.

Conversely, assume that the hesitant fuzzy setFof Heyting algebraLsatisfies conditions (F3) and (F4). ThenhF(1) =hF(x) for anyx∈Lby 1 ≥xand (F3). By Theorem 2.1(8), we havex∧ (x→y) =x∧yfor anyx,y∈L. It follows from (F3) and (F4) thathF(y) ⊇hF(x∧y) =hF(x∧ (x→y)) ⊇hF(x) ∩hF(x→y). ThereforeFis a hesitant fuzzy filter ofL.

Corollary 3.3A hesitant fuzzy setFof Heyting algebraLis a hesitant fuzzy filter ofLif and only if it satisfies (F3) and the conditionhF(x∧y) =hF(x) ∩hF(y) for anyx,y∈L,

ProofObviously,x≥x∧yandy≥x∧yfor allx,y∈L, it follows from (F3) thathF(x∧y) ⊆hF(x) andhF(x∧y) ⊆hF(y), sohF(x∧y) ⊆hF(x) ∩hF(y). Combining (F4), we can complete the proof.

Theorem 3.4IfFandGbe two hesitant fuzzy filters of a Heyting algebraL, thenF∩G, defined byh(F∩G)(x) =hF(x) ∩hG(x) for anyx∈L, is a hesitant fuzzy filter ofL.

ProofFor anyx,y,z∈Lwithx∧y≤z, we get thathF(z) ⊇hF(x) ∩hF(y) andhG(z) ⊇hG(x) ∩hG(y) by Corollary 3.2, and sohF(z) ∩hG(z) ⊇ (hF(x) ∩hF(y)) ∩ (hG(x) ∩hG(y)) = (hF(x) ∩hG(x)) ∩ (hF(y) ∩hG(y)), which impliesh(F∩G)(z) ⊇h(F∩G)(x) ∩h(F∩G)(y). ThereforeF∩Gis a hesitant fuzzy filter ofL.

Corollary 3.4IfF(i)(i∈I) be hesitant fuzzy filters of a Heyting algebraL, then ∩i∈IF(i), defined by (∩i∈IF(i))(x) = (∩i∈IF(i)(x) for anyx∈L, is a hesitant fuzzy filter ofL.

Theorem 3.5For a filterHof Heyting algebraL, letFbe a hesitant fuzzy set onLdefined by

for allx∈Lwhereγ,τ∈P([0,1]) withγ⊃τ. ThenFis a hesitant fuzzy filter ofL.

ProofSince 1 ∈H, we havehF(1) =γ⊇hF(x) for allx∈L. For anyx,y∈L, ify∈H, then clearlyhF(y) =γ⊇hF(x) ∩hF(x→y). IfyH, then at least one ofxandx→ydoes not belong toH. HencehF(y) =τ=hF(x) ∩hF(x→y), and thereforeFis a hesitant fuzzy filter ofL.

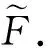
Ifx∉Fτorx→yFτ, then= ∅ or(x→y) = ∅. Thus(x→y).

Theorem 3.7Let F be a hesitant fuzzy set on a Heyting algebraLand leta∈L. Then

(1) If Ωais a filter ofL, thenFsatisfies the following condition:

(F5) (∀x,y∈L)(hF(a) ⊆hF(x) ∩hF(x→y) ⟹hF(a) ⊆hF(y)).

(2) IfFsatisfies (F1) and (F5), then Ωais a filter ofL.

Proof(1) Assume that Ωais a filter ofL. Letx,y∈Lbe such thathF(a) ⊆hF(x) ∩hF(x→y). Thenx∈ Ωaandx→y∈ Ωa. By using (H2), we have y ∈ Ωaand sohF(y) ⊇hF(a).

(2) Suppose thatFsatisfies (F1) and (F5). From (F1) it follows that 1 ∈ Ωa. Letx,y∈Lbe such thatx∈ Ωaandx→y∈ Ωa. ThenhF(a) ⊆hF(x) andhF(a) ⊆hF(x→y), which imply thathF(a) ⊆hF(x) ∩hF(x→y). ThenhF(a) ⊆hF(y) by (F5), and soy∈ Ωa. Therefore Ωais a filter ofL.

Letf:L→L′ be a homomorphism of Heyting algebras andFa hesitant fuzzy set onL′ . Define a mappinghf-1(F):L→P([0,1]) such thathf-1(F)(x) =hF(f(x)), for allx∈L. Obviously,hf-1(F)(x) is well-defined andf-1(F) is a hesitant fuzzy set onL.

Theorem 3.8Letf:L→L′ be an onto homomorphism of Heyting algebras andFa hesitant fuzzy set onL′ . ThenFis a hesitant fuzzy filter ofL′ if and only iff-1(F) is a hesitant fuzzy filter ofL.

4 Several special hesitant fuzzy filters of Heyting algebras

Definition 4.1A hesitant fuzzy filterFof Heyting algebraLis said to be a hesitant fuzzy Boolean filter ofLifhF(x∨x-) =hF(1) for allx∈L.

Theorem 4.1LetLbe a Heyting algebra andFa hesitant fuzzy filter ofL. ThenFis a hesitant fuzzy Boolean filter ofLif and only if the setFτ= {x∈L|τ⊆hF(x)} is a Boolean filter ofLfor anyτ∈P([0,1]) withFτ≠ ∅.

ProofBy Theorem 3.1,Fis a hesitant fuzzy filter ofLif and only ifFτis a filter ofLfor anyτ∈P([0,1]) withFτ≠ ∅. Suppose thatFis a hesitant fuzzy Boolean filter, and letτ∈P([0,1]) be such thatFτ≠ ∅. ThenFτis filter ofL, and so 1 ∈Fτ, i.e,hF(1) ⊇τ. It follows thathF(x∨x-)=hF(1) ⊇τfor anyx∈L, hencex∨x-∈Fτ. ThereforeFτis a Boolean filter ofL.

Conversely, assume thatFτis a Boolean filter ofLfor anyτ∈P([0,1]) withFτ≠ ∅. Then lethF(1)=γ, soFγis a Boolean filter ofL. Hencex∨x-∈Fγfor allx∈L, which implieshF(x∨x-) ⊇γ=hF(1). On other hand, sinceFa hesitant fuzzy filter ofLand 1 ≥x∨x-, it follows from (F3) thathF(1) ⊇hF(x∨x-) for allx∈L. SohF(1)=hF(x∨x-) for allx∈L, and henceFis a hesitant fuzzy Boolean filter ofL.

Corollary 4.1LetFbe a hesitant fuzzy filter of Heyting algebraL. Then F is a hesitant fuzzy Boolean filter ofLif and only if the setFhF(1)is a Boolean filter ofL.

Theorem 4.2LetFandGbe two hesitant fuzzy filters of a Heyting algebraLsatisfyinghF(1)=hG(1) andhF(x) ⊆hG(x) for allx∈L. IfFis a hesitant fuzzy Boolean filter ofL, then so isG.

ProofSinceFis a hesitant fuzzy Boolean filter ofL, we havehG(1)=hF(x∧x-) ⊆hG(x∨x-) for anyx∈L. SinceGbe a hesitant fuzzy filter of a Heyting algebraL, it follows from (F1) thathG(x∨x-) ⊆hG(1), and sohG(x∨x-)=hG(1) for allx∈L. ThereforeGis a hesitant fuzzy Boolean filter ofL.

Theorem 4.3LetHbe a nonempty subset of Heyting algebraL. Define a hesitant fuzzy setFonLas follows

for allx∈Lwhereγ,τ∈P([0,1]) withγ⊃τ. IfHis a Boolean filter ofL, thenFis a hesitant fuzzy Boolean filter ofL.

ProofSuppose thatHis a Boolean filter ofL. Then by Theorem 3.5,Fis a hesitant fuzzy filter ofL. SinceHis Boolean, we havex∨x-∈Lfor allx∈L, and sohF(x∨x-)=γ=hF(1∨1 )=hF(1). ThereforeFis a hesitant fuzzy Boolean filter ofL.

Definition 4.2A hesitant fuzzy filterFof Heyting algebraLis called a hesitant fuzzy implicative filter ofLifhF(x→z) ⊇hF(x→ (z-→y)) ∩hF(y→z) for anyx,y,z∈L.

The proofs of the following two theorems are similar to Theorem 4.1 and Theorem 4.3, respectively.

Theorem 4.4LetLbe a Heyting algebra andFa hesitant fuzzy filter ofL. ThenFis a hesitant fuzzy implicative filter ofLif and only if the setFτ={x∈L|τ⊆hF(x)} is an implicative filter ofLfor anyτ∈P([0,1]) with Fτ≠ ∅.

Theorem 4.5LetHbe a nonempty subset of Heyting algebraL. Define a hesitant fuzzy setFonLas follows

for allx∈Lwhereγ,τ∈P([0,1]) withγ⊃τ. IfHis an implicative filter ofL, thenFis a hesitant fuzzy implicative filter ofL.

Theorem 4.6LetFbe a hesitant fuzzy filter of Heyting algebraL. Then the following are equivalent:

(1)Fis a hesitant fuzzy implicative filter ofL.

(2) (∀x,z∈L)(hF(x→z) ⊇hF(x→ (z-→z))).

(3) (∀x,z∈L)(hF(x→z)=hF(x→ (z-→z))).

(4) (∀x,y,z∈L)(hF(x→z) ⊇hF(y→ (x→ (z-→z))) ∩hF(y)).

Proof(1)⟹(2): ifFis a hesitant fuzzy implicative filter ofL, thenhF(x→z) ⊇hF(x→ (z-→z)) ∩hF(z→z)=hF(x→ (z-→z)) ∩hF(1)=hF(x→ (z-→z)) for allx,z∈Lby (F1).

(2)⟹(3): Fromx→z≤z-→ (x→z)=x→ (z-→z) and (F3), we havehF(x→z) ⊆hF(x→ (z-→z)). Using (2), the proof of the condition (3) is completed.

(3)⟹(4): SinceFis a hesitant fuzzy filter ofL, it follows from (F2) thathF(x→ (z-→z)) ⊇hF(y→ (x→ (z-→z))) ∩hF(y) for allx,y,z∈L. By (3), we havehF(x→z) ⊇hF(y→ (x→ (z-→z))) ∩hF(y) for allx,y,z∈L.

(4)⟹(1): Obviously,hF(x∧z-→y)∩hF(y→z) ⊆hF(x∧z-→z), i.e.hF(x→ (z-→y))∩hF(y→z) ⊆hF(x→ (z-→z)). By (4), (hF(x→z) ⊇hF(1 → (x→ (z-→z)))∩hF(1)=hF(x→ (z-→z)), and so (hF(x→z) ⊇hF(x∧z-→y) ∩hF(y→z) for allx,y,z∈L. ThereforeFis a hesitant fuzzy implicative filter ofL.

Theorem 4.7LetFbe a hesitant fuzzy filter of Heyting algebraL. ThenFis Boolean if and only ifFis implicative.

ProofSuppose thatFis a hesitant fuzzy Boolean filter ofL. Then by (F2), Definition 4.1 and (F1), we havehF(x→z) ⊇hF((z∨z-) → (x→z)) ∩hF(z∨z-)=hF((z∨z-) → (x→z)) ∩hF(1)=hF((z∨z-) → (x→z)) for anyx,y,z∈L. Since (z∨z-) → (x→z)= (z→ (x→z)) ∧ (z-→ (x→z)=(x→ (z→z))∧(x→ (z-→z)=(x→ (z-→z), it follows thathF(x→z) ⊇hF(x→ (z-→z)) for anyx,y,z∈L. ThereforeFis a hesitant fuzzy implicative filter ofLby Theorem 4.6.

Conversely, assume thatFis a hesitant fuzzy implicative filter ofL. Then by Theorem 4.6, we have thathF((x-→x) →x)=hF((x-→x) → (x-→x))=hF(1) andhF((x→x-) →x-)=hF((x→x-) → (x--→x-))=hF((x-→x-) → (x→x-))=hF(1) for allx∈L. It follows thathF(x∨x-)=hF((x→x-) →x-) ∩hF((x-→x) →x)=hF(1) for allx∈L, and henceFis a hesitant fuzzy Boolean filter ofL.

Definition 4.3LetFbe a hesitant fuzzy set of a Heyting algebraL. F is called a hesitant fuzzy positive implicative filter ofLif it satisfies (F1) and the condition: for anyx,y,z∈L,hF(x→z) ⊇hF(x→ (y→z)) ∩hF(x→y).

In MTL-algebras, the hesitant fuzzy positive implicative filter has some interesting properties. We will see that the hesitant fuzzy positive implicative filter is equivalent to the hesitant fuzzy filter in Heyting algebras.

Theorem 4.8LetFbe a hesitant fuzzy set of a Heyting algebraL. ThenFis a hesitant fuzzy positive implicative filter ofLif and only ifFis a hesitant fuzzy filter ofL.

ProofSuppose thatFis a hesitant fuzzy positive implicative filter ofL, thenhF(1 →z) ⊇hF(1 → (y→z)) ∩hF(1 →y), i.e.,hF(z) ⊇hF(y→z)) ∩hF(y) for ally,z∈L. Hence,Fis a hesitant fuzzy filter ofL.

Conversely, assume thatFis a hesitant fuzzy filter ofL, thenhF(x→ (y→z)) ∩hF(x→y) ⊆hF(x→ (x→z))=hF(x→z) for allx,y,z∈L. HenceFis a hesitant fuzzy positive implicative filter ofL.

Definition 4.4A hesitant fuzzy filterFofLis called a hesitant fuzzy ultra filter ofLif, for anyx∈L,hF(x)=hF(1) orhF(x-)=hF(1).

Definition 4.5A hesitant fuzzy filterFofLis called a hesitant fuzzy obstinate filter ofLif it satisfies:

(∀x,y∈L)(hF(x)≠hF(1),hF(y)≠

hF(1) ⟹hF(x→y)=hF(1).

The proofs of the following theorems are similar to Theorem 4.1, Theorem 4.3, Theorem 3.6 and Theorem 3.8, respectively.

Theorem 4.9LetFbe a hesitant fuzzy set of Heyting algebraL. ThenFis a hesitant fuzzy positive implicative (ultra, obstinate) filter ofLif and only if the setFτ={x∈L|τ⊆hF(x)} is a positive implicative (an ultra, an obstinate) filter ofLfor anyτ∈P([0,1]) withFτ≠ ∅.

Theorem 4.10LetHbe a nonempty subset of Heyting algebraL. Define a hesitant fuzzy setFonLas follows

for allx∈Lwhereγ,τ∈P([0,1]) withγ⊃τ. IfHis a positive implicative (an ultra, an obstinate) filter ofL, thenFis a hesitant fuzzy positive implicative (ultra, obstinate) filter ofL.

Corollary 4.2LetFbe a hesitant fuzzy filter of Heyting algebraL. ThenFis a hesitant fuzzy ultra (obstinate) filter ofLif and only if the setFhF(1)is an ultra (obstinate) filter ofL.

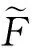
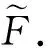
Theorem 4.12Letf:L→L′ be an onto homomorphism of Heyting algebras andFa hesitant fuzzy set onL′ . ThenFis a hesitant fuzzy Boolean (implicative, positive implicative, ultra, obstinate) filter ofL′ if and only iff-1(F) is a hesitant fuzzy Boolean (implicative, positive implicative, ultra, obstinate) filter ofL.

Theorem 4.13LetFandGbe two hesitant fuzzy filters of a Heyting algebraLsatisfyinghF(1)=hG(1) andhF(x) ⊆ hG(x) for allx∈L. IfFis a hesitant fuzzy ultra (obstinate) filter ofL, then so isG.

ProofThe proof is similar to Theorem 4.2 and omitted.

5 Conclusions

Uncertainty usually appears in many real world problems. Fuzzy sets and its extensions have become a very powerful tool to deal with uncertainty in different problems. As another generalization of fuzzy sets, the concept of hesitant fuzzy sets has been introduced in [21], which permits the the membership degree of an element to be a set of several possible values. Subsequently, many operators for hesitant fuzzy sets have been introduced to handle the real decision making problems.

Heyting algebra is an important algebraic model in lattice theory and logic, and was extensively investigated by some researchers. Filter theory of Heyting algebras plays a very significant role in studying algebraic structure of Heyting algebras. In this paper, we apply the theory of hesitant fuzzy sets to Heyting algebras. We introduce the concepts of hesitant fuzzy (Boolean, implicative, positive implicative, ultra, obstinate) filters of Heyting algebras, then study their properties involving the homomorphic preimages of these hesitant fuzzy filters. We also provide conditions for a hesitant fuzzy set to be a hesitant fuzzy filter of Heyting algebras, discuss some equivalent characterizations, and establish extension theorem of hesitant fuzzy Boolean (ultra, obsyinate) filters. On the basis of these results, we will study applications of hesitant fuzzy sets to several ideals and filters of MTL-algebras, MV-algebras, R0-algebras, and so forth.