基于数学史料 设置问题探究 提升数学思维
——以“从勾股定理到图形面积关系的扩展”为例
吴超萍 刘 鹏 陈 璐 杨光伟 (浙江师范大学教师教育学院 321004)
《义务教育数学课程标准(2011年版)》设计了“综合与实践”板块,要求通过教师的问题引领,学生全程参与其中,从而激发创造的潜能.在教学过程中,教师要注意观察、积累、分析、反思,使“综合与实践”的实施成为提高教师自身素质和学生素质的互动过程.[1]要真正将“综合与实践”落实到课堂中,探究教学是一个不错的教学方式.汪晓勤指出,一个数学主题的产生与发展往往与前人解决问题的过程和方式密不可分,因而数学历史成为数学探究教学的一个很好的载体.[2]基于历史的数学问题可以作为课堂教学环节设计中的一部分,让学生体会知识发展的过程、积累数学经验以及获得成功的体验,并对数学产生更浓厚的兴趣.
1 教学过程
1.1 引今据典,创设情境
师:通过上节课对勾股定理的学习,我们对勾股定理的发展历史和定理公式有了一定的了解.在西方,最早提出并证明该定理的是古希腊的著名数学家毕达哥拉斯,因此勾股定理也称为毕达哥拉斯定理.
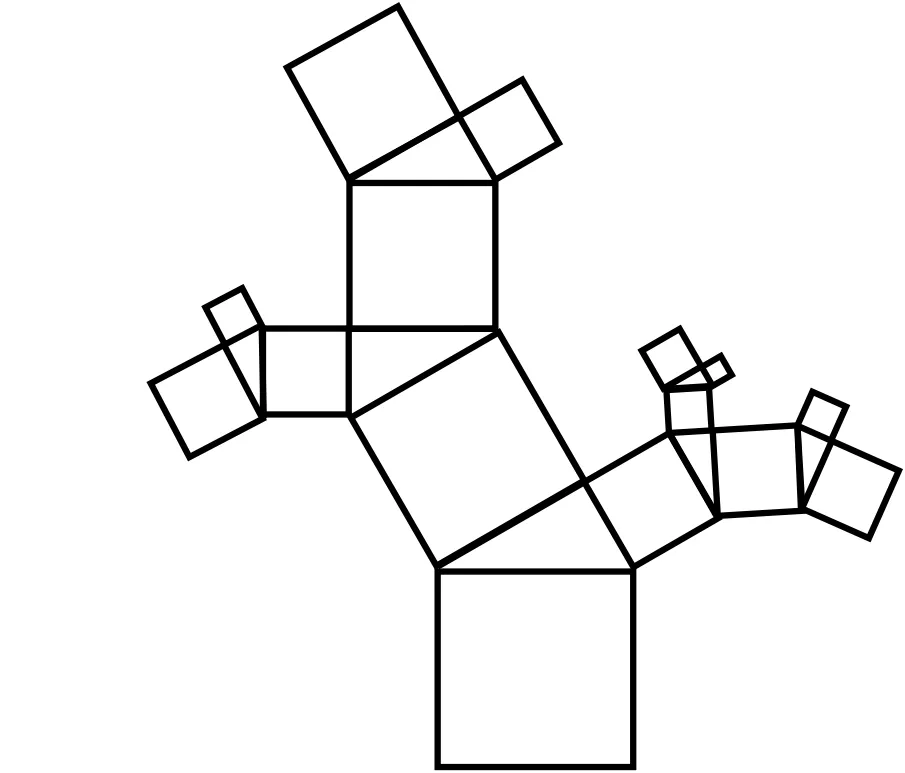
图1
问题1对数学家们来说,数学研究是一件富有创造、有趣的事.毕达哥拉斯利用勾股定理构造出了一棵树的模型,你能通过观察发现这个模型在构成上有什么特点吗?(图1)
生:这个模型都是由一组基本图形重复出现构成的.
师:非常好,我们今天就从这个基本图形出发,探究勾股定理与图形面积之间的关系.
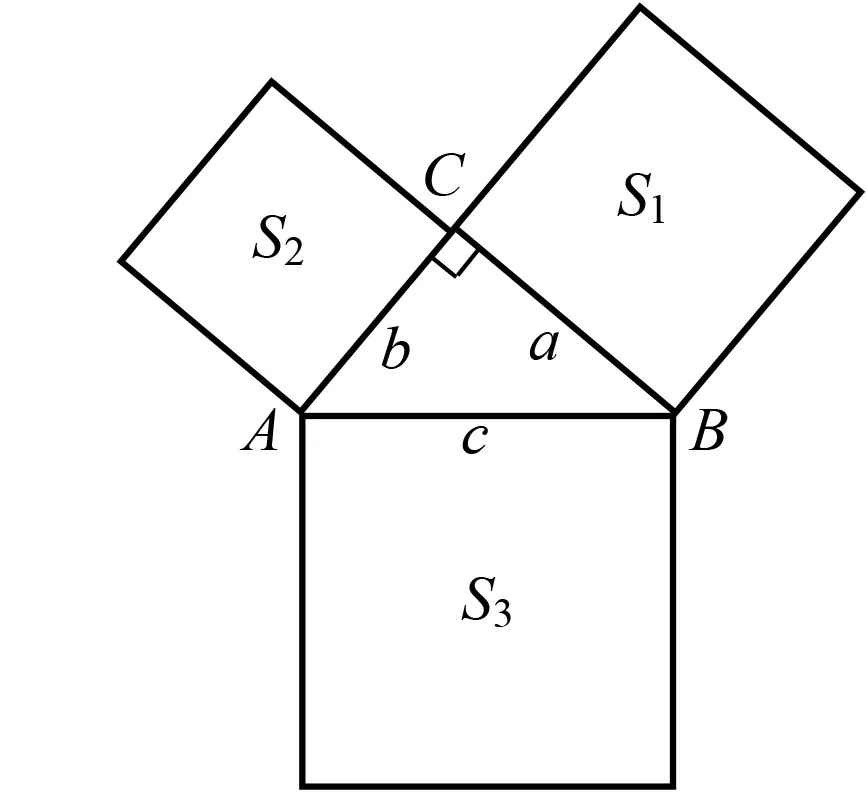
图2
问题2将这一组基本图形单独画出来,如图2所示,在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,分别以a,b,c为边长向外作正四边形,面积分别为S1,S2,S3,问S1,S2,S3之间存在何种联系?如何证明?
学生思考,小组探究.
教师通过学生反馈的答案得到两个小正方形的面积之和等于大正方形的面积的结论.不难发现,因为S1=a2,S2=b2,S3=c2,根据勾股定理可知a2+b2=c2,所以S1+S2=S3.
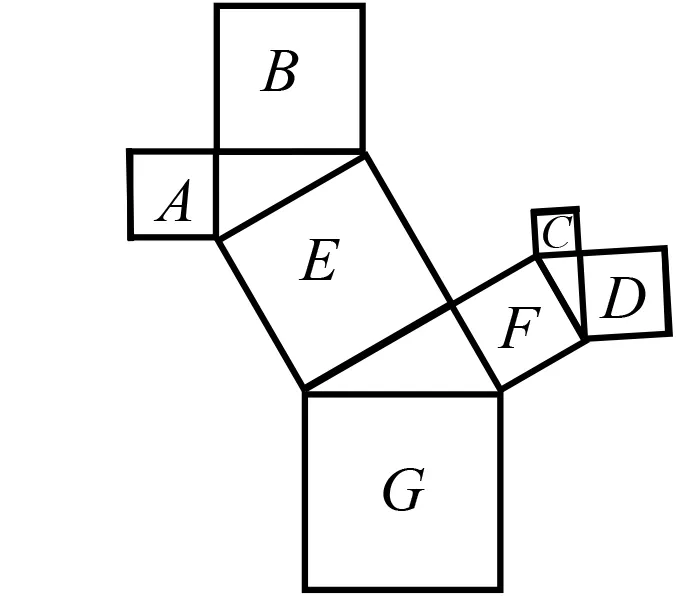
图3
问题3再请同学们思考,图3所示为是一株美丽的勾股树,其中所有的长方形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别是9,25,4,9,则最大正方形G的面积是多少?
生:可以利用刚刚得到的结论求出答案.因为正方形A和正方形B的面积之和等于正方形E的面积,正方形C和正方形D的面积之和等于正方形F的面积,推出正方形E和正方形F的面积之和等于正方形G的面积,所以正方形G的面积为47.
设计意图通过勾股树(毕达哥拉斯树)引起学生的兴趣,以问题串的形式引导学生发现基本图形中正方形之间的关系,为后面的探究奠定基础.
1.2 知识迁移,举一反三
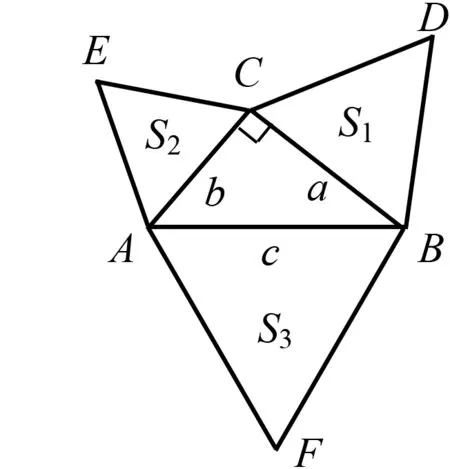
图4
问题4如果将基本图形中的正方形变成三角形(图4),此时S1,S2,S3之间是否存在某种关系?
学生自主探究.
师:在基本图形中,我们得到了两个小正方形的面积之和等于大正方形的面积的结论.我们能否用类比的思想得到相同或相似的结论呢?
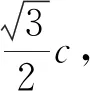
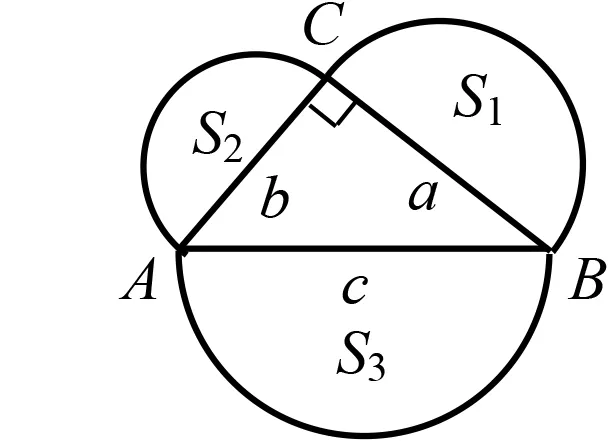
图5
师(追问):如果向外作半圆呢?结论是否依旧成立?

师:其实在欧几里得时代,人们就对勾股定理的一些扩展问题进行过研究,在《欧几里得·几何原本》第6卷第31个命题中记载着:“在直角三角形中,斜边上任意所画的图形等于两条直角边上所画的与前图形相似且有相似位置的二图形的和.”[3]
设计意图由三角形向外作正方形推广到三角形向外作三角形和半圆,在学生的最近发展区构建桥梁,在学生现有的认知水平上一点点增加难度,旨在培养学生发现问题和解决问题的能力,同时引入历史上相关的数学片段,引起学生的共鸣.
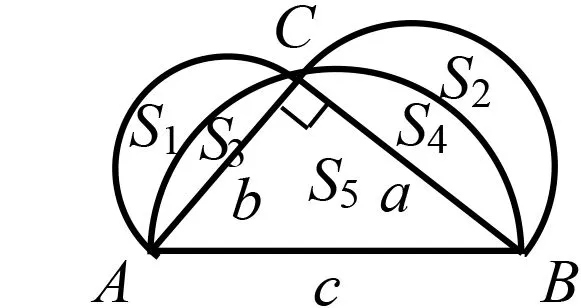
图6
问题5此时,我们将图5中的半圆S3向上翻折,得到图6,翻折过后的图形S1,S2,S5之间有怎样数量关系呢?你可以想出几种得到答案的方法?
学生思考,小组探究.
生:根据问题4中得到的结论可知,直角边上两个半圆面积之和等于斜边上半圆的面积. 即(S1+S3)+(S2+S4)=S3+S4+S5,所以S1+S2=S5.
师:其实在公元前400年左右,古希腊数学家希波克拉底研究了自己所画的半圆图形,得出了类似的结论,这个定理也被称为月牙定理[4],也就是我们刚刚一同讨论的图案.
1.3 解决问题,积累经验
问题6将图2中最大的正方形向上翻折,得到图7,试问图形S1,S2,S3,S4的面积与Rt△ABC之间有什么数量关系?前后四人为一小组展开讨论,并请学生分享成果.
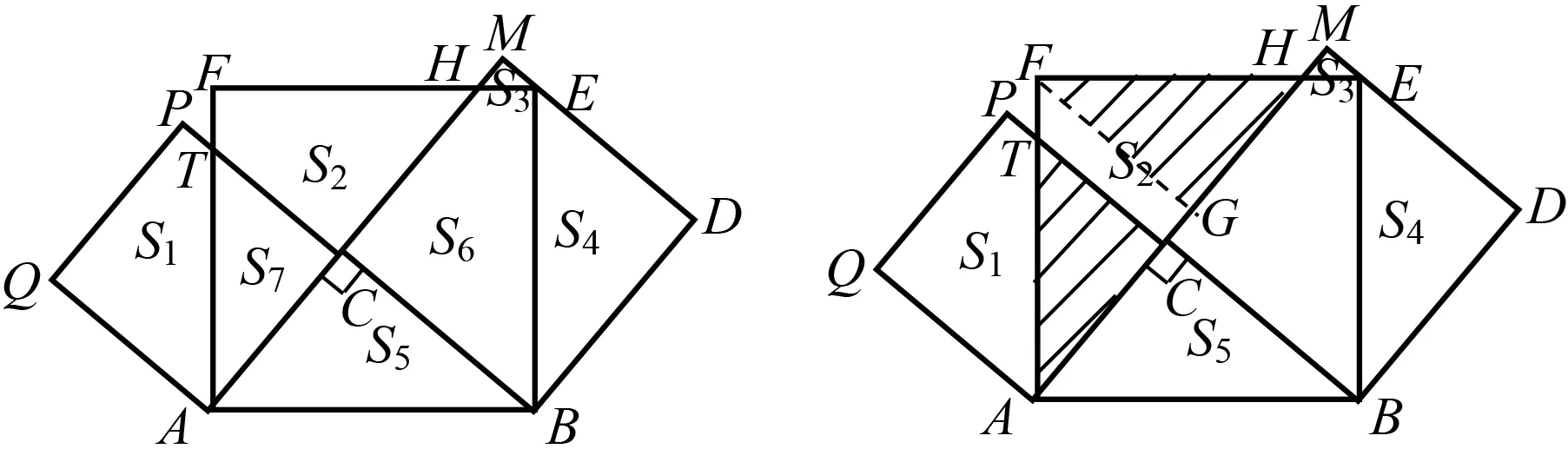
图7 图8
生:根据两个小正方形面积之和等于大三角形的面积,可得S1+S7+S3+S4+S6=S2+S5+S6+S7,化简得S1+S3+S4=S2+S5,两边同时加上S2,得到S1+S2+S3+S4=2S2+S5.过F作AM的垂线交AM于点G,容易证明 △AGF≌△ACB,△ACT≌△FGH,得到S2=S5,从而推出S1+S2+S3+S4=3S5.
师:大家利用已知的知识进行探索,最终得到了解题的方法.
设计意图整个探究过程层层递进,都是在前一问的基础上逐步加入新的情况.从毕达哥拉斯树中抽取的基本图形引出本节课,经过对正三角形、圆的面积关系计算,最后又回到毕达哥拉斯树中的基本图形,用不同的方式进行提问,将代数与几何的知识巧妙地结合起来,并利用数形结合思想扩展学生的思路,提高学生的创新能力.
1.4 应用扩展,深化理解
师:接下来我们在此基础上进行简单的应用和扩展,感受数学的魅力与奇妙.
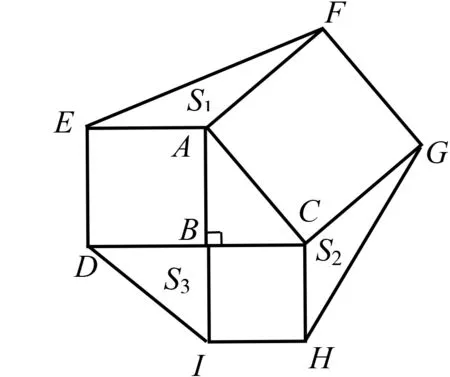
图9
例1(2011·济南)如图9所示,△ABC为直角三角形,且AB>BC,现分别以△ABC的边AB,BC,AC为一边向外作正方形ABDE,BCHI,ACFG,同时连结EF,GH,DI,设△AEF,△CHG,△BDI的面积分别为S1,S2,S3,则下列结论正确的是( ).
A.S1=S2=S3
“好啊,今天太好啦,比打胜仗还要高兴。没想到咱团来了一个‘甜同志’,不但让同志们吃到了她的喜糖,还给大家带来了甜甜的节目。很好啊。”团长把手中扣着的盆子,仔细揭起一层,原来是两个,又分别扣下去。“这新郎新娘究竟是谁呢?现在,我宣布——”
B.S1=S3 C.S1=S2 D.S3=S2 例2(2019·宁波)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中曾有记载.以直角三角形的各边为边分别向外作正方形(图10),再把较小的两张正方形纸片按图11的方式放置在最大正方形内.如果知道图中阴影部分的面积,则一定能求出( ). 图10 图11 A.直角三角形的面积 B.最大正方形的面积 C.较小两个正方形重叠部分的面积 D.最大正方形与直角三角形的面积和 问题7在课上我们探讨了外接正三角形和外接正四边形,如果我们继续类比,向外作正五边形、正六边形……其图形面积之间的数量关系是否依旧满足S1+S2=S3呢? 设计意图通过设置问题、循序诱导、解答疑问,引导学生去发现问题和解决问题.由学生自己探究出解决这一类问题的思路和方法. 本节课的内容位于浙教版数学八年级上册第二章,是“从勾股定理到图形面积关系的扩展”的阅读材料.很多教师对于此类内容不会进行详细探究,这对学生思维的发展是不利的.勾股定理作为几何学的基石,其等式能够衍生出很多数学问题,将勾股定理与图形面积相联系,是对学生进行思维训练的一次很好的机会. 数学史作为数学教学中重要的文化素材,它的引入能够使原本枯燥的课堂变得有趣,激起学生的求知欲.因此,在本节课教学的开始阶段,教师通过介绍毕达哥拉斯树引出本节课的探究问题,抓住学生的注意力;在课堂进行过程中,对几何原本中记载的相关知识进行提炼讲解,并在恰当的时刻融入希波克拉底发现的月牙定理,加深学生对该定理的理解,拓展学生的知识面. 在教学过程中,应避免将结论直接告诉学生,而应尽可能通过问题的设定引导学生思考、讨论、回答,让学生有更多的机会参与课堂,从而激发探究欲望.本节课中,教师首先是对外接正方形图形面积关系提问,其次是对外接正三角形和半圆图形面积关系提问,再次是对半圆翻折图形面积关系提问,最后回到正方形翻折图形面积来提问,引导学生一步步进行深度探究.学生利用直角三角形向外作不同形状的图形得到结论,在探究过程中感受到数学的魅力、学习的快乐以及成功的喜悦. 弗赖登塔尔曾指出:“没有一种数学的思想,是以它被发现时的那个样子公开发表出来的,一个问题被解决后,相应地发展为一种形式化技巧,结果把求解过程丢在一边,使得火热的发明变成冰冷的美丽.”[5]在本节课中,教师利用毕达哥拉斯树中的基本图形引导学生发现其中的面积关系,而发现的过程是解决这一类问题的精髓部分.题目可以千变万化,但其中蕴含的方法是一样的,教师在探究教学过程中让学生围绕本质的求解方式进行思考,同时通过题目和问题让学生检验自己的掌握程度,有利于拓宽其思维以更好地解题.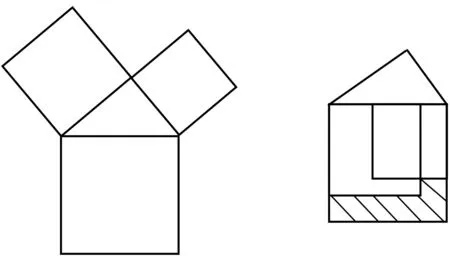
2 反思总结
2.1 融入数学故事,提升学习兴趣
2.2 设置问题探究,激发探究欲望
2.3 揭示数学本质,启迪数学思维

