翅片管冷凝器低压环境下空气侧换热特性研究

张汝行 柳建华,2 张 良

(1 上海理工大学能源与动力工程学院 上海 200093； 2 上海市动力工程多相流动与传热重点实验室 上海 200093)

翅片管冷凝器作为热泵系统的空气处理设备和高效换热装置，一直都是研究人员研发和改进的热点。1971年，F. C. McQuistion等[1]率先提出了平翅片换热器空气侧换热模型，其传热因子的预测偏差达34.4%。随后， Wang C. C.等[2-3]通过研究翅片管换热特性提出了被广泛认可的传热因子关联式。W. Pirompugd等[4]利用有限环肋法全面地分析了各种工况下的翅片换热，并建立了湿工况的传热传质关联式。Ma Xiaokui等[5]研究发现湿工况下传热因子和传质因子随着翅片间距的增加而增大。N. H. Kim等[6]研究发现条缝翅片的摩擦因子大于平翅片的摩擦因子，且增幅随管排数的增加而变大。鞠培玲等[7]研究了翅片管换热器在析湿工况下的积灰特性及积灰对空气侧压降的影响，结果表明翅片表面的析湿量决定积灰程度，积灰程度与摩擦压降成正比。最近，谷波等[8]研究了两种不同类型的光滑波纹翅片的空气侧性能，并对已有实验关联式进行了修正。随着高原地区的发展以及浮空平台技术的应用，热泵开始逐渐应用于低压工况中。在常压环境下，翅片管冷凝器的空气侧热阻远大于管内侧，是强化换热的主攻方向。但低压下空气的密度较低，表征对流换热的空气侧雷诺数减小，可知翅片管冷凝器的对流换热表面传热系数较常压下有明显区别。胡松涛等[9]测试了电加热器在常压和低压环境下的表面传热系数和散热功率，认为电加热器表面传热系数与环境气压的0.2次幂成正比。林晖等[10]利用G-M低温制冷机，测量和分析了低温低压条件下水平圆管自然对流换热特性，并给出了无量纲实验准则式。王晶等[11]研究了竖直平板在不同环境压力(0.001～101 kPa)和加热量(75、150、300 W/m2)下的散热，结果表明对流换热表面传热系数在绝对气压小于1 kPa时非常小，可视为0；在绝对气压大于1 kPa时，对流换热表面传热系数随压力的升高呈2次幂增加。刘旗等[12]对低压湿工况下的蒸发器进行研究，研究了刘易斯因子的变化规律和影响因素，并引入了压力修正因子。张嘉文等[13-14]总结了目前具有较高认可度的空气侧理论换热模型，并根据低压下蒸发器换热特性对模型进行了修正。

现阶段有关低压下翅片管换热器的少量研究主要针对蒸发器，空气侧属于冷却过程且过程中伴随着析湿传质，而冷凝器则是完全的显热交换。在Dittus-Boelter[15]的强制对流关联式中，加热流体与冷却流体存在明显的不同。

目前，有关翅片管式冷凝器在低压环境下通过空气散热的研究非常少。本文搭建了一个翅片管冷凝器在低压下的换热实验台，研究低压环境对翅片管换热器空气侧对流换热的影响，同时验证现有常压下翅片管换热模型在低压条件下的适用性。

1 实验系统

低压换热实验系统如图1所示。实验系统由翅片管冷凝器、环境仓、电加热、加湿器、循环风机、真空泵、温湿度传感器、压力传感器、采集仪组成。为提高耐压强度及密封性，环境仓采用不锈钢材料构成封闭环形。环境仓包括循环段与测试段：循环段为DN350的圆形通道，测试段为500 mm×500 mm的矩形通道。电加热器和真空泵能根据实验要求调节换热器入口空气的温度以及环境仓压力。在测试段入口前布置均流板，以确保测试段的气流均匀性。在翅片管冷凝器的进出口处装有温湿度传感器，在环境舱内布置多个压力传感器，用于检测环境仓内各点的状态参数。采用变频轴流风机调节空气循环量，并使用微压差传感器测量喷嘴前后压差，根据喷嘴的前后压差测量空气的循环量。测试系统主要包括实验参数的数据采集和运行工况的参数控制。实验通过AGILENT采集仪与LabVIEW软件实现数据参数的采集与显示。

1真空泵；2电加热器；3循环风机；4微压差传感器；5压力传感器；6调节阀；7均流板；8标准喷嘴；9温湿度传感器；10翅片管冷凝器；11流量调节阀；12热水循环系统。

翅片管冷凝器采用三角形错列排列方式，具体翅片管参数和结构如表1和图2所示。由于制冷剂的冷凝温度较难控制，实验中利用40～50 ℃的热水作为管内的换热工质。循环热水的进出温度由两个Pt100温度传感器测得，其校准精度为0.1 ℃。循环热水的体积流量由涡轮转子流量传感器测得，热水温度通过PID控制器调节。在实验操作中，数据的稳定性判断参考ASHRAE 41.2-2018标准[16]，即空气侧与水侧的热平衡偏差应小于5%。实验工况：风速为1～4 m/s，环境压力为40～101 kPa，纵向管排数为2～4排，入口水温为40～50 ℃。

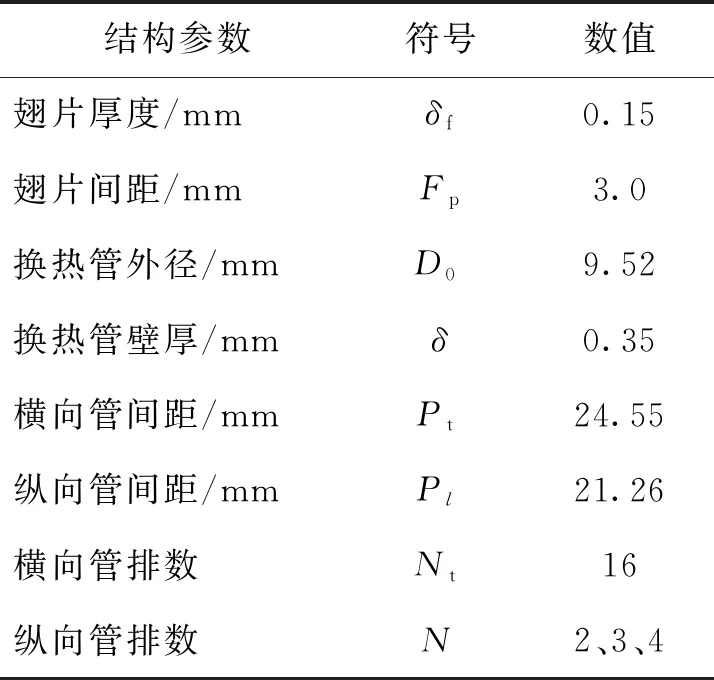
表1 翅片管冷凝器结构参数

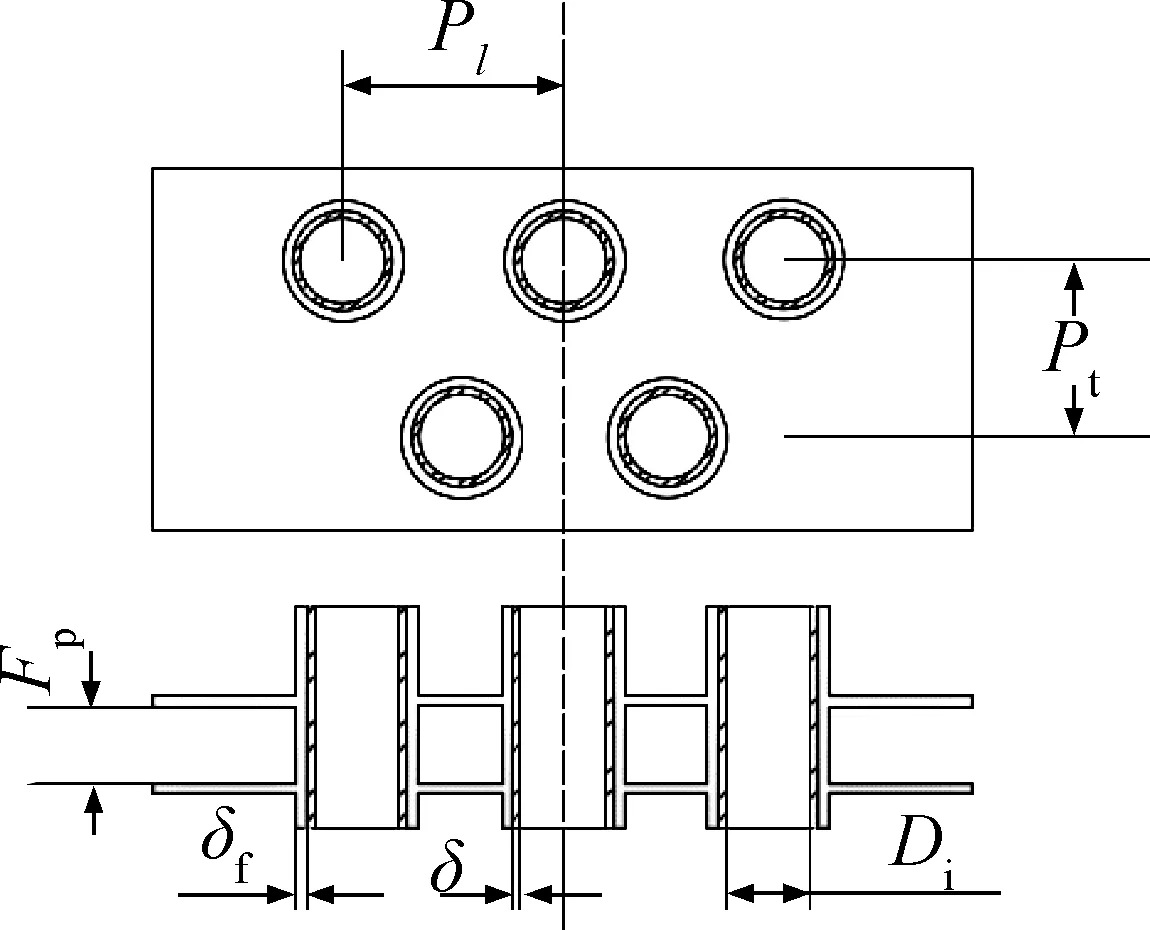
图2 翅片管冷凝器的结构

实验前首先进行常压下换热实验，将常压下的实验数据与换热模型[17]进行对比，结果表明最大相对偏差为28.4%，最小相对偏差为9.3%。这表明该实验系统的设置合理、可靠性较高。

2 数据处理

2.1 传热计算

传热量Qair：

Qair=cpmair(tout,air-tin,air)

(1)

Qair=KAΔtm

(2)

对数平均温差Δtm：

(3)

式中：cp为空气的定压比热容，kJ/(kg·K)；mair为空气的质量流量，kg/s；tin,air、tout,air分别为冷凝器的进、出口空气温度，℃；tin,w、tout,w分别为热水的进、出口温度，℃；A为管外总表面积，m2。

冷凝器的传热系数K：

(4)

式中：λt为紫铜管导热系数，W/(m·K)；Ab为肋片间管外总表面积，m2；Ai为管内总表面积，m2；hw、hair分别为管内侧水、管外侧空气的对流换热表面传热系数，kW/(m2·K)；ηf为翅片效率；δ为管壁厚度，m。

管内热水的物性温度为进出口的平均温度，流速根据质量流量计测得。利用Dittus-Boelter[15]公式或Gnielinski[18]公式计算管内循环热水的对流换热表面传热系数hw：

Dittus-Boelter[15]公式：

(5)

Gnielinski[18]公式：

(6)

fR为摩擦因子，采用下式计算：

fR=(1.58lnRew-3.28)-2

(7)

翅片效率：

(8)

(9)

(10)

式中：r0为管外半径，m；R0为等效半径，m；Rew为水侧雷诺数；Prw为水的普朗特数；λw为水的导热系数，W/(m·K)；Di为管内直径，m；φ、M为翅片效率的计算参数；δf为翅片厚度，m；λf为翅片的导热系数，W/(m·K)；ifg为饱和水的气液潜热，kJ/kg。

等效半径R0：

R0=1.28W(L/W-0.2)1/2

(11)

式中：L为翅片长度，m；W为翅片宽度，m。

利用上式对各参数进行计算，最后代入式(2)中得到对流换热表面传热系数hair。

2.2 实验的不确定度分析

由于测量仪器存在精度等级，实验过程中也会存在系统误差。为提高实验数据的可信度，利用Moffat[19]法对重要数据进行不确定分析。

Moffat[19]的不确定度计算方法：

假设影响U的一系列参数有：

U=U(X1,X2,X3,……Xn)

(12)

则U的合成不确定度为：

(13)

经计算，本实验数据的不确定度如表2所示。

表2 实验不确定度

3 数据分析

图3所示为实验测得的不同环境压力和最窄面空气侧雷诺数Reair下对流换热表面传热系数的变化，翅片管换热器入口空气的干球温度为25 ℃，翅片管换热器的热水入口温度为45 ℃，管排数为2。随着Reair的降低，对流换热必然降低。由图3可知，在最窄面Reair为400～800的范围内，随着环境压力的降低，对流换热表面传热系数曲线的斜率明显减小。说明在低压环境下Reair与对流换热的关系式发生改变。当Reair=400时，环境压力从101 kPa降至40 kPa，对流换热表面传热系数降低了44.1%。即在相同的Reair下，随着环境压力的降低，空气侧的对流换热明显减弱。由此可推断环境压力的降低抑制了空气侧扰动对换热的强化。原因分析如下：在翅片结构未发生改变的情况下，虽然雷诺数具体值相同，但环境压力的降低导致空气密度降低，单位体积内空气质量的减小必然会减小空气中的各分子与加热壁面的有效接触次数，因此空气侧的对流换热表面传热系数减小。

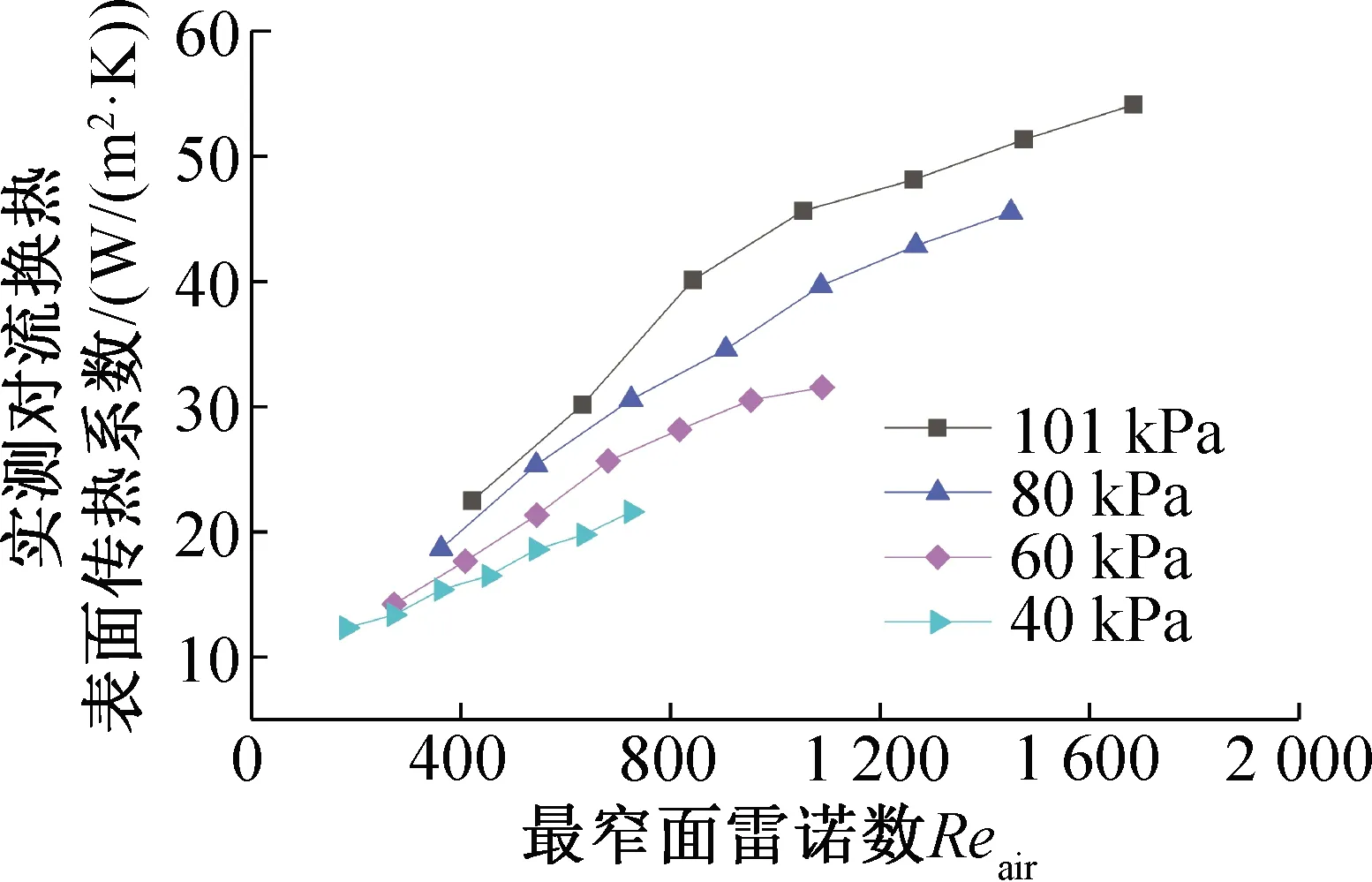
图3 不同环境压力和最窄面空气侧雷诺数时对流换热表面传热系数的变化

图4所示为管排数为2排，空气流速为2.5 m/s时，不同环境压力和加热温度下空气侧对流换热表面传热系数的变化。由图4可知，在40～101 kPa环境压力中，当循环热水入口温度从40 ℃升至50 ℃，空气侧的对流换热没有发生明显的规律性变化，表明对流换热与管内外工质的流动参数、换热面的结构有关，与温差的大小无关。这与常压条件下循环热水温度不会影响换热的结论是一致的。

图5所示为不同环境压力下管排数对对流换热的影响。随着纵向管排数的增加，空气侧的摩擦阻力增加，导致空气的扰动程度降低，造成对流换热略有减小。此外，随着环境压力的降低，管排数对对流换热的影响逐渐变弱。由此推断低压环境会削弱翅片结构对空气侧对流换热的影响。原因是随着环境压力的降低，Reair开始减小，黏性力的作用开始增强，对流换热变弱，因而宏观层次上翅片结构对换热的影响得到削弱。

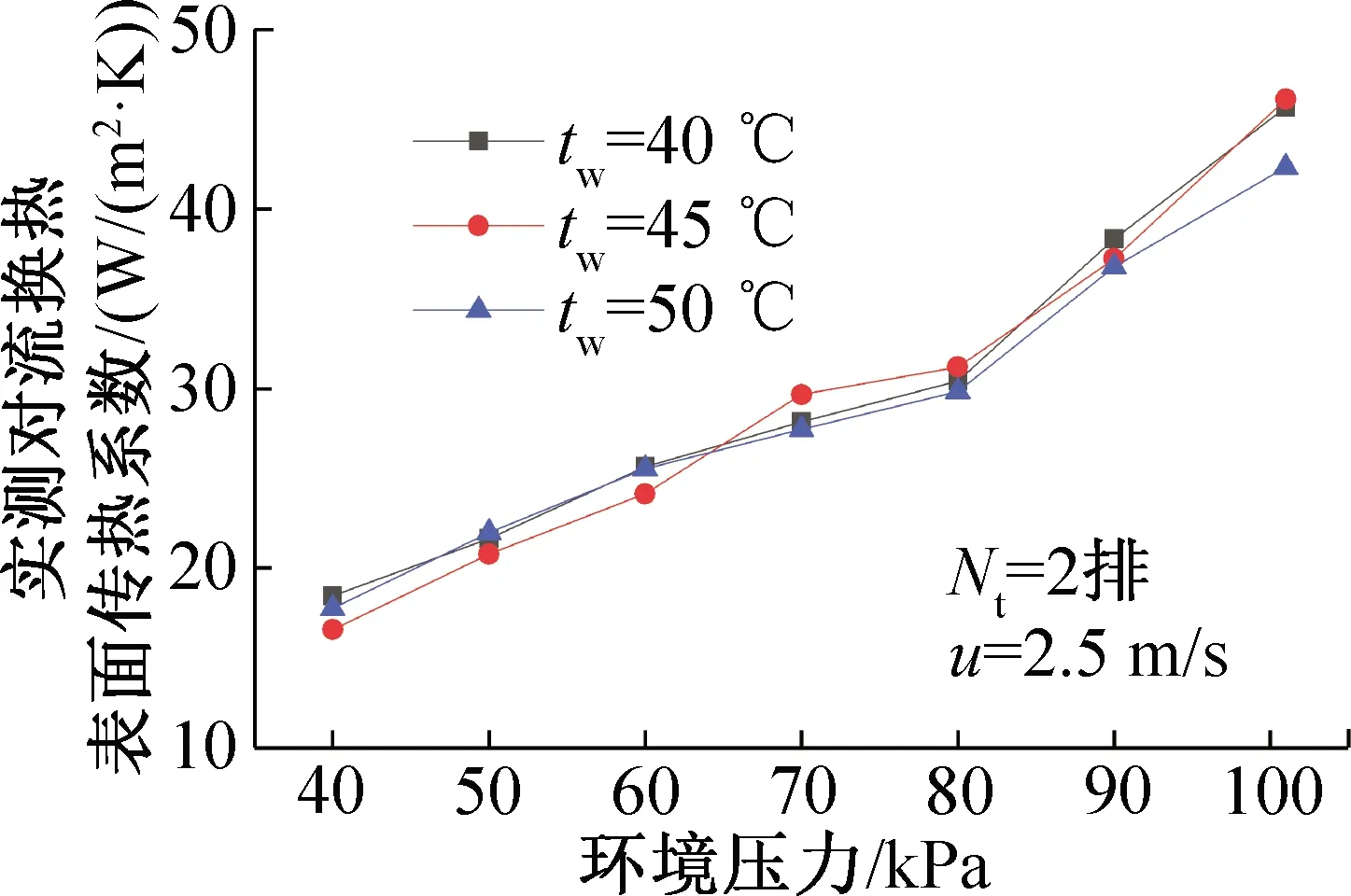
图4 不同环境压力和热水温度时对流换热表面传热系数的变化

图5 不同环境压力和管排数时对流换热表面传热系数的变化

将实测的对流换热表面传热系数与常压换热模型[17]的计算结果进行对比，结果如图6所示。随着环境压力的降低，实测对流换热表面传热系数明显小于常压换热模型[17]的计算结果，而且压力越低偏移越大，当环境压力从101 kPa降至40 kPa时，平均偏差从17.3%增至77.5%。

常压下的对流换热表面传热系数计算模型[17]：

(14)

m=-0.28+0.08Reair/1 000

(15)

n=0.45+0.006 6L/deq

(16)

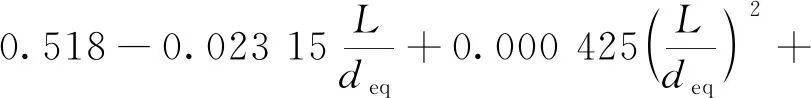
(17)

c=A(1.36-0.24Reair/1 000)

(18)

式中：λair为空气导热系数，W/(m·K)；L为翅片片宽，m；deq为当量直径，m；Reair为最窄面的空气侧雷诺数。

由式(14)可知，当环境压力改变时，主要变量是空气侧雷诺数，较大的偏差也证明随着环境压力的降低，雷诺数对空气侧对流换热的影响变弱。

针对现有预测模型的局限性，根据不同环境压力和纵向管排数下的实测对流换热表面传热系数，对常压换热模型[17]进行修正，并且得到了适用于40～90 kPa压力范围内的修正因子B，如式(19)～式(20)，其R2=0.995，修正模型的对流换热表面传热系数与实测对流换热表面传热系数的对比如图7所示，两者的平均绝对偏差为9.5%。

(19)

(20)

式中：pl为低压环境压力，kPa；pa为标准大气压力，kPa，Nt为横向管排数。

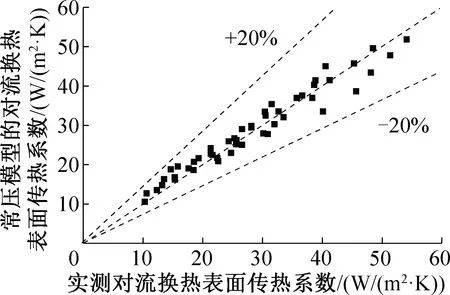
图7 对流换热表面传热系数的修正

4 结论

本文研究了低压环境下平翅片管冷凝器的空气侧换热特性，分析了低压环境下空气侧雷诺数、管排数及加热温度与空气侧对流换热的关系，得到如下结论：

1)在相同的空气侧雷诺数下，随着环境压力的降低，空气侧的对流换热明显减弱。在空气侧雷诺数为400时，环境压力从101 kPa降至40 kPa，对流换热表面传热系数降低了44.1%。

2)低压环境下，增加管排数会降低对流换热，这也与常压下的空气侧换热特性相同，但随着环境压力的降低，管排数对对流换热的影响也会变弱。从实验结果来看，改变循环热水温度没有对低压下的空气侧换热产生明显影响。

3)随着环境压力的降低，实测对流换热表面传热系数开始小于常压模型的计算结果。当环境压力从101 kPa降至40 kPa，平均偏差从17.3%增至77.5%。针对现有预测模型的局限性，结合环境压力、管排数对空气侧对流换热的影响，对常压模型进行修正，修正后的平均绝对偏差为9.5%。