大坝防渗墙设计参数优化研究
崔宏伟
(辽宁润中供水有限责任公司,辽宁 辽阳 111000)
1 工程背景
泡子沿水库位于辽宁省法库县柏家沟镇泡子岩村境内的辽河二级支流王河干流上,是一座以防洪为主,兼有灌溉、供水和养殖等诸多功能的综合性中型水利工程[1]。该水库的地理位置十分重要,下游保护辽北工业重镇铁法市,3个煤矿以及20万人口,同时还可以为当地工业提供360万m3的优质水源。水库大坝为均质土坝,坝体为粉质黏土,主坝的坝基从上而下分别为粉质黏土层、砂砾层和基岩层。其中,基岩层上部为强风化花岗岩,下部为弱风化花岗岩。泡子沿水库建成于20世纪50年代,不仅设计建设标准低,且没有完整的设计建设资料,属于典型的“三边”工程。
在经过近70年的运行之后,病险问题日渐突出,特别是渗漏问题十分严重,当上游来水水位上涨后,会在坝后形成沼泽,这不仅会造成水资源的流失,还会影响到大坝的安全[2]。虽然期间进行过多次盖重处理,但是仍旧存在比较严重的安全隐患。因此,辽宁省各级政府积极筹措资金,对该水库进行全面除险加固。针对大坝的渗漏问题,通过对坝体和坝基地质条件的深入分析,拟采用混凝土防渗墙和高压喷射灌浆进行处理,保证大坝和水库的安全运行。基于此,本文以数值模拟的方法,展开防渗墙设计参数的优化研究,以期为加固工程设计施工提供支持。
2 研究方法
2.1 计算模型的构建
由于本文主要研究不同防渗墙的防渗作用和效果,因此选择能够全面反映泡子沿水库大坝特征的Ⅲ-33断面作为数值模拟研究的计算断面,因为该断面的防渗墙高度最大,土体材料也能反映大坝的整体情况[3]。
在几何模型的构建过程中,以水平方向指向下游的方向为X轴的正方向,以竖直向上的方向为Y轴的正方向,以坝体上游与基岩地面交界部位为坐标原点。为了准确模拟大坝的渗流情况,结合相关研究成果和工程经验,模型的计算范围为坝体上游10 m至坝体下游15 m,整个计算模型的长度为121.5 m,高32.5 m[4]。
在进行泡子沿水库大坝的有限元计算模型构建过程中,由于防渗墙要深入坝基基岩,因此在计算中要考虑基岩对混凝土防渗墙的嵌固作用[5]。计算模型采用的是以摩尔-库伦准则为基础的弹塑性有限元模型[6]。所有的结构均采用四边形等参单元进行模拟,在防渗墙和土体之间设置Goodman接触单元,以有效模拟新建的混凝土防渗墙和土体之间的接触状态[7]。最终,整个模型被划分为15 750个计算单元和18 970个计算节点,有限元模型的示意图如图1所示。
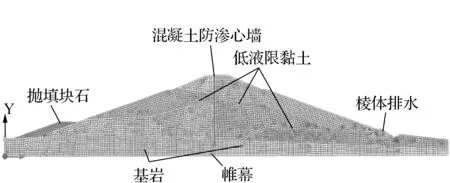
图1 有限元模型示意图
2.2 边界条件与荷载
结合相关研究经验,在计算过程中主要考虑的荷载有大坝坝体的自重、静水压力、渗透压力以及接触面的摩擦力[8]。为了充分考虑水库的极端运行情况,计算在水库的校核洪水工况下进行,此时大坝的上游水位为40.96 m,下游水位为28.71 m。由于本次研究计算是大坝在蓄水并形成稳定渗流工况,因此采用间接耦合的方法考虑渗流场的影响。大坝基础的上下游垂直剖面以及底面为不透水面,上游库水位以下的表面以及下游水位以下的表面为已知水头边界条件;大坝下游水位以上的坝体表面为可能渗流逸出面。
2.3 计算参数
计算的参数取值对计算结果存在十分显著的影响,本次研究由于缺少原始设计资料,因此主要通过实际地质勘查资料和相关类似工程资料获取,各部分材料所使用的渗透系数值如表1所示。

表1 模型材料的渗透系数 m/s
2.4 计算工况
在防渗墙的施工设计过程中,主要应该考虑的参数有两个分别是防渗墙的厚度以及嵌入弱透水层(弱风化基岩)的深度。对防渗墙的厚度而言,其厚度越厚,防渗效果越好,但是会明显增加施工成本。参考相关工程设计经验,中小型土石坝的防渗墙厚度一般不超过1.3 m。但是,对除险加固工程施工而言,厚度小于0.6 m的防渗墙需要采取冲击钻施工方式,而厚度减小节省的成本并不能弥补钻孔量增加产生的经济代价,因此并不具有经济性和防渗优势。基于此,本文设计了0.6 m、0.8 m、1.0 m和1.2 m四种不同的防渗墙厚度进行计算分析。由于本工程基岩上部的弱风化层厚度为12 m左右,因此,设计了0 m、2 m、4 m、6 m、8 m、10 m和12 m等七种不同嵌入深度,上述两个参数的不同水平值相互组合,获得如表2所示的计算工况。

表2 计算工况设计表
3 计算结果与分析
3.1 单宽渗流量计算结果与分析
利用构建的有限元模型,对不同计算工况下的坝基单宽渗流量进行计算,并根据计算结果,绘制出如图2所示的单宽渗流量随防渗墙入岩深度的变化曲线。由图可知,坝基的单宽渗流量随着防渗墙的厚度和入岩深度的增加而减小,说明增加防渗墙的厚度和入岩深度,可以取得更好的防渗效果。但是,随着防渗墙厚度和入岩深度的增加,降低单宽渗流量的作用会明显降低,而施工成本会大幅增加,结合施工设计中5.27×10-4m3/s的单宽渗流量允许值,认为厚0.8 m,入岩深度 2 m的防渗墙参数设计最为合适。

图2 单宽渗流量随防渗墙入岩深度的变化曲线
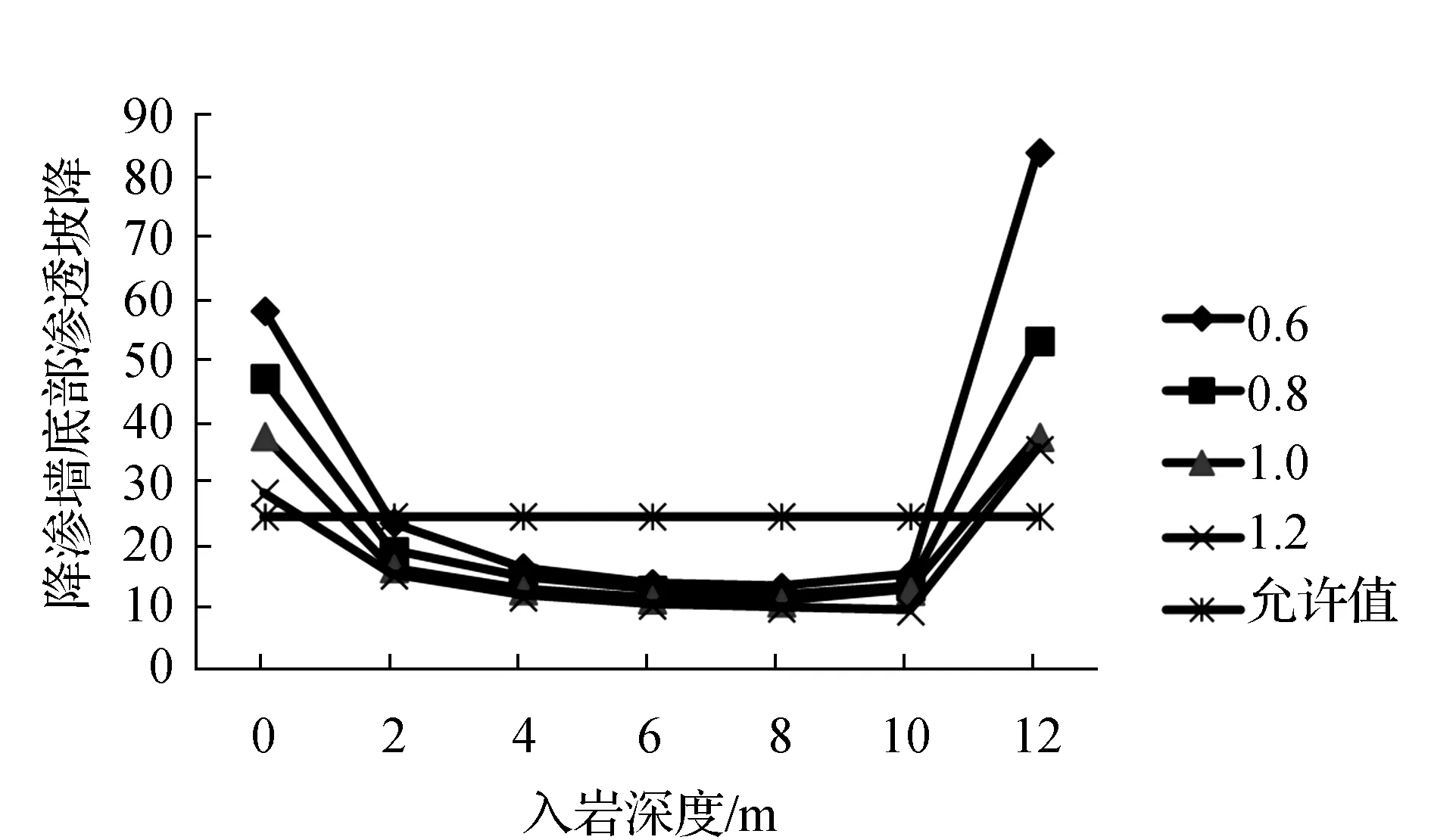
图3 防渗墙底部渗透坡降随防渗墙入岩深度的变化曲线
3.2 防渗墙底部渗透坡降计算结果与分析
利用构建的有限元模型,对不同计算工况下的防渗墙底部渗透坡降进行计算,并根据计算结果,绘制出如图3所示的防渗墙底部渗透坡降随防渗墙入岩深度的变化曲线。由图可知,在增设防渗墙之后,在防渗墙的底部会出现比较显著的渗透坡降集中现象,当防渗墙的入岩深度小于8 m的情况下,防渗墙底部渗透坡降会随着入岩深度的增大而减小,当入岩深度大于8m时防渗墙底部渗透坡降会随着入岩深度的增大而增大,特别是入岩深度由10 m增大到12 m的过程中,防渗墙底部渗透坡降出现骤增的特征,并超过25的允许值。究其原因,主要是随着入岩深度的增加,防渗墙下部的水流渗流通道不断减小,从而造成渗流速度的增大,由此造成的局部水头损失和底部水头差的叠加,导致该部位渗透坡降的上升,特别是防渗墙接近微风化岩层时,其底部的渗流通道变得极小,因此产生极大的渗流速度,进而导致渗透坡降的骤然增加。由此可见,从防渗墙底部渗透坡降这一要素来看,过大的入岩深度并不利于大坝安全,最佳入岩深度应该在2~10 m。
3.3 坝脚逸出点渗透坡降计算结果与分析
利用构建的有限元模型,对不同计算工况下的坝脚溢出点渗透坡降进行计算,并根据计算结果,绘制出如图4所示的坝脚溢出点渗透坡降随防渗墙入岩深度的变化曲线。由图可知,坝脚溢出点渗透坡降随防渗墙入岩深度的增大而减小,但是减小的速率先快后慢。究其原因,主要是增加防渗墙的入岩深度,会显著增加水体的渗流长度,从而造成水头损失,最终导致渗透坡降的减小。从具体的数值来看,防渗墙厚度0.8 m,入岩深度2 m的情况下,防渗墙底部和坝脚溢出点的渗透坡降均小于允许值,而进一步增加防渗墙的厚度和入岩深度,无疑会大幅增加施工成本和难度。同时,入岩深度过大,还会大幅增加基岩对防渗墙的约束作用,对防渗墙的应力控制不利。因此,防渗墙厚度为0.8 m,入岩深度2.0 m最为经济合理。
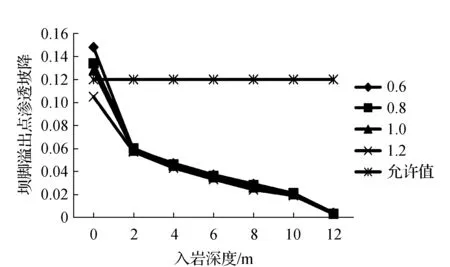
图4 坝脚溢出点渗透坡降随防渗墙入岩深度的变化曲线
4 结 论
(1)坝基的单宽渗流量随着防渗墙的厚度和入岩深度的增加而减小,说明增加防渗墙的厚度和入岩深度,可以取得更好的防渗效果。
(2)防渗墙底部渗透坡降会随着入岩深度的增大呈现出先减小后迅速增大的特征,过大的入岩深度并不利于大坝的安全稳定。
(3)坝脚溢出点渗透坡降随防渗墙入岩深度的增大而减小,但是减小的速率先快后慢。
(4)结合模拟计算结果以及工程的经济性,认为防渗墙厚度为0.8 m,入岩深度2.0 m最为经济合理。

