基于高分辨率遥感影像的花粒期玉米叶面积指数估算方法
任枫荻,陈圣波,陈彦冰
(吉林大学 地球探测科学与技术学院,吉林 长春 130026)
0 引言
叶面积指数(Leaf Area Index, LAI)反映单位土地面积上植物叶片的总面积,是反映作物群体特征的重要指标,是表征植被冠层结构和反映植被长势的重要生理参数[1,2]。目前进行LAI测量的方法有直接法和间接法两种。直接法是指使用仪器实地测量叶面积指数,结果较为准确,但是耗时耗力,并会造成叶片组织的损伤,且测量结果并不具有普遍代表性,因此,仅仅适用于部分地区的验证性测量。间接法是指采用遥感手段进行大范围的植被指数估算。遥感技术具有时空分辨率高、数据采集成本低以及可以实现大面积、宽领域、实时动态监测等优势[3-4],为估算大范围植被的LAI提供了有效的技术手段。
利用间接法获取叶面积指数的模型方法分为经验模型和物理模型两类。经验模型是以 LAI为因变量,以光谱数据或其变换形式(例如植被指数)作为自变量建立的估算模型,是目前国内外利用遥感技术来估算叶面积指数的主要方法[5]。随着遥感卫星数据的普及,前人利用HJ卫星影像生成了HJVI、NDVI、EVI等7种数据,构造了夏玉米LAI的估算模型[6]。还有人采用GF-1和Landsat8遥感影像,开展了叶面积指数的估算研究[7]。根据遥感影像可以提取植被指数,建立植被指数与叶面积指数间的关系模型,从而估测LAI。有学者对比研究了10个常见植被指数与不同生育时期LAI的相关性及预测性,筛选出预测LAI的最佳植被指数和最优模型[8]。在众多植被指数中,利用EVI建立的叶面积指数估算模型的精度优于同类植被指数模型[9]。对多种常见植被指数的估算效果进行简单的回归分析后得出,用EVI估算LAI是具有较高精度的[10]。物理模型法需要利用大量的物理参数模拟农作物的生长过程,适用性比较好,多应用于农作物物理数据丰富、参数齐全情况下的LAI建模。物理模型方法种类较多,利用PROSAL辐射传输模型[11]、建立神经网络估算模型[12]、采用随机森林算法[13]都可以准确估算所研究作物的LAI。但由于物理模型法需要测量作物的许多生理物理参数用作输入,模型过于复杂,难以推广应用。
目前遥感卫星影像具有高空间分辨率、高清晰度、信息量丰富及数据时效性强等优点,可以提供更多地物的细节信息,因此针对卫星数据的LAI估算模型优选和真实性检验日益得到重视[14]。前人对于估算玉米叶面积指数的研究多为整个玉米生长期的综合研究,而单独对某一时期针对性的研究较少,并且适于玉米不同生育期的叶面积指数估算模型应是不同的,鉴于此,我们主要对玉米花粒期的叶面积指数估算进行了研究。本研究基于吉林省中部地区玉米花粒期的多种植被指数与实测LAI数据,提取相关性较好的植被指数,进行线性和非线性相关分析,构建回归分析模型,最终对模型进行了验证分析,检验所建模型的适用性和可靠性。
1 研究区域和数据源
1.1 研究区域概况
本研究的5个实验地区位于吉林省中部,其在吉林省的位置如图1。吉林省平均每年日照时数为2259~3016 h,年平均降水量为400~600 mm,冬季平均气温在-11 ℃以下,夏季平原平均气温在23 ℃以上。吉林省具有优质的土壤和丰富的土地资源,光、热、水分条件可以满足作物生长需要,农作物以玉米为主。根据吉林省玉米生长时期和气候条件,玉米于5月初播种,8月上旬进入玉米的花粒期,9月下旬逐步进入成熟期。

图1 研究区的相对位置图
1.2 影像数据源
本文所用的卫星遥感数据来自美国Planet Labs遥感卫星群, Planet Labs(PL)影像有蓝(485 nm)、绿(545 nm)、红(630 nm)、近红外(820 nm)4个标准光谱波段,空间分辨率为3 m。本文采用的遥感影像数据对应地区和日期分别是蛟河市2019年9月11日、永吉县2019年8月28日和2019年9月14日、舒兰市2019年9月1日、德惠市2019年9月1日和2019年9月11日,以及农安县2019年9月11日。
1.3 实测数据
本研究采用地面安装的农情监测设备传输的数据,数据于2019年8月17日开始采集,于2019年9月17日结束采集。农情监测设备分布在5个实验地区的玉米地块内。该设备可在每1个样点测量记录作物的株高、冠层大小、叶片面积等物候信息,后期设备传输的数据计算出叶面积指数,作为该样点的有效LAI值。同时利用GPS定位仪记录每1个设备位置的经纬度。
2 研究方法
针对PL卫星遥感数据,应用ENV I5.3软件计算出多种广泛使用的植被指数,结合实验地区玉米的地面实测LAI数据,利用SPSS Statistics 20软件采用多种回归模型进行LAI估算,对比不同模型的输出结果,并分析不同模型的估算精度,最后筛选出最佳估算模型。
2.1 植被指数的选取
植被指数(Vegetation Index, VI)是用两个或多个波长范围内的地物反射率进行线性或非线性组合运算,产生某些对植被长势、生物量等有一定指示意义的专题数值[15]。本文在建立LAI-VI关系时,为了探讨不同因素对于估算LAI的影响,选取了比较常见且被广泛使用的植被指数:增强植被指数EVI[16]、归一化植被指数NDVI[17]、比值植被指数RVI[18]、优化土壤调节植被指数OSAVI[19]以及土壤调节植被指数SAVI[20],以LAI为因变量,以不同类型的植被指数为自变量,建立LAI估算回归模型。
在进行回归分析之前,首先在SPSS Statistics 20软件中依次分析选取的植被指数与LAI之间的相关关系。依据统计学中的相关规定,当相关系数的绝对值在0.6~0.8时为强相关。本文分析了各类植被指数与实测叶面积指数间的相关性。由表1可知,玉米的LAI与各植被指数间的相关系数均高于0.6,说明这几种植被指数均与LAI呈强相关,其中EVI与LAI的相关性最强,SAVI与LAI的相关性较强,因此本文只选取增强植被指数EVI和土壤调节植被指数SAVI进行研究。选取的植被指数对玉米LAI的变化较灵敏,适合构建经验回归模型。其中,EVI对基础数据进行了全面的大气校正,并对土壤背景的影响作了处理,因此它是综合处理土壤、大气、饱和问题的植被指数,是对NDVI的继承和改进。另一植被指数SAVI的提出主要是用来减少植被指数对不同土壤反射变化的敏感性,有效地降低了土壤背景的影响,改善了植被指数与叶面积指数间的关系。

表1 植被指数与LAI间的相关系数
2.2 植被指数回归模型的构建
将玉米实测LAI与EVI和SAVI这2种植被指数进行相关分析后,分别应用线性、对数、二次曲线、幂函数、S曲线以及指数形式模型与对应的LAI进行回归拟合,利用判定系数R2筛选出拟合LAI精度最高的回归模型。判定系数的结果如表2所示。
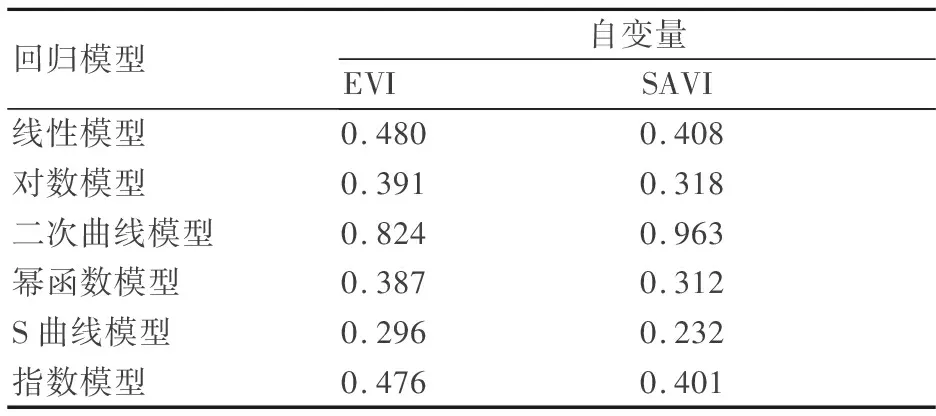
表2 不同回归模型的判定系数
从表2中可以看出:两种植被指数作自变量时拟合效果最好的模型均是二次曲线模型,其次是线性模型;两种植被指数相对比,采用以SAVI作自变量的二次曲线模型的拟合效果又优于以EVI作自变量的二次曲线模型。所以在这6种模型中,玉米LAI拟合效果最佳的回归模型是以SAVI作自变量的二次曲线模型。各植被指数最优的回归方程如图2所示。

a为EVI估算的最佳回归方程。b为SAVI估算的最佳回归方程。
3 结果与分析
由表2可以看出,在LAI-VI二次曲线回归模型建立中,二次曲线回归模型的R2都大于0.5,具有较好的拟合效果。本文选取5个实测的玉米LAI数据作为回归模型的建模样本,用剩余的两个数据作为验证数据,并利用最优回归模型计算出样本点的估测LAI值。
3.1 模型估算结果
用于验证的两个LAI数据分别为4.476和4.524。对第1个验证数据,利用EVI建立的模型估测的LAI值为4.581,用SAVI建立的模型估测的LAI值为4.565;对第2个验证数据,利用EVI建立的模型估测的LAI值为4.680,用SAVI建立的模型估测的LAI值为4.647。说明用SAVI估算的玉米LAI值比其他植被指数的估算结果更加接近于地面实测的LAI值。
3.2 精度验证结果
本文采用均方根误差(Root Mean Square Error,RMSE)和相对误差(Relative Error,RE)这两个指标对所建立的回归模型进行精度验证。其中RMSE是衡量观测值与真实值之间的偏差,常用来作为模型预测结果衡量的标准。而RE指测量所造成的绝对误差与被测量真值之比乘以100%所得的数值,以百分数表示。一般来说,RE更能反映测量的可信程度。
精度验证结果:以EVI建立的回归模型验证的RMSE为0.133,RE为2.896%;基于SAVI回归模型验证的RMSE为0.107,RE为2.352%。在物理意义上当RE小于5%时证明所建模型的估测精度较高,因此这两个模型的估测精度均较高。各植被指数模型的RMSE值都小于0.3,说明各模型的估测精度均较高,其中SAVI模型的RMSE最低,只有0.107,故此模型的估测效果最好。因此,在吉林省中部的这5个地区可以利用SAVI植被指数所建立的二次曲线回归模型来估算花粒期玉米的叶面积指数。
4 小结与讨论
本次研究以吉林省中部5个地区为研究区,选取5种常用植被指数进行分析,根据相关系数筛选相关性较好的两种植被指数SAVI和EVI,分别建立6种线性与非线性统计回归模型,最终利用判定系数指标来选取估算叶面积指数的最优回归模型。结果表明,拟合精度最高的模型是以SAVI为自变量的二次曲线回归模型,其估算值与地面实测值较为一致,这进一步为农作物遥感理论研究和应用提供了理论依据。本研究结果如下:5种常用植被指数与LAI间的相关系数均大于0.6,其中SAVI和EVI与LAI间的相关系数居前2位;在以SAVI和EVI这2个植被指数作自变量所建立的12种模型中,采用以SAVI作自变量的二次曲线模型估算花粒期玉米叶面积指数的效果最佳,其方程式为y=17.986x2-14.109x+7.324,相关系数为0.728,相对误差为2.352%,均方根误差为0.107,其拟合精度和适用性较强,可用于获取高精度的玉米LAI信息。

