新型全机能数控车床进给系统伺服电机的惯量扭矩匹配计算
丁伟明,邵志骋,刘春阳,徐武军
(中国通用技术集团大连机床有限责任公司,辽宁 大连 116620)
0 引言
进给系统是CNC系统和移动部件间的执行系统,是数控车床的重要组成部分[1]。在市场化运作的当下,车床产品更加偏向于移动部件轻量化(小惯量)、绿色化(低耗能)方向设计,进给伺服电机是动力源的关键要素之一,因此选型显得尤为重要。目前进给系统伺服电机的惯量扭矩匹配计算仍存在两个关键性问题:①没有完整的、系统性的文献可供参考;②依赖于供应商的伺服电机选型软件(只有结果,没有过程),无法优化。本文根据新型全机能数控车床的设计实例及现有量销产品的反复验证,提出了通用型选型方法,本方法具有借鉴意义。
1 新型全机能数控车床X轴移动部件参数
新型“阶梯平”全机能数控车床由中国通用技术集团大连机床有限责任公司数控车床研究所研发设计,该车床结构紧凑、运行平稳、精度可靠。由于采用斜床身、平导轨结构,避免在了在粗、精加工时多次使用角度胎而造成的产品精度不一致问题,大大提高了装配效率。目前该产品已形成量产,其车床截面如图1所示。
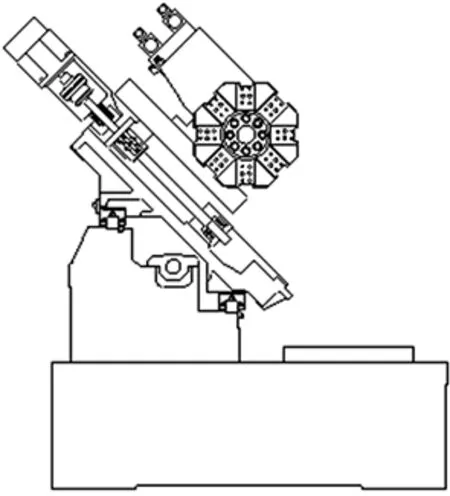
图1 “阶梯平”全机能数控车床斜床身、平导轨结构图
设计目标参数:移动部件质量W=220 kg;丝杠长L=0.618 m;螺距Ph=8 mm;初选丝杠外径d=28 mm;初选丝杠底径d0=22.4 mm;初选快移速度V=20 000 mm/min;床体角度θ=45°;初选伺服电机惯量J电=0.001 17 kg·m2;联轴器惯量J联=0.000 617 kg·m2;传动效率η=0.95;动摩擦系数μ=0.02;密度ρ=7800 kg/m3;重力加速度g=9.8 N/kg;传动比i=1(直联)。
2 X轴进给伺服电机惯量匹配
惯量对进给系统的精度、稳定性,动态响应都有影响[2-3],设计时应使移动部件的惯量需和进给伺服电机的惯量相匹配才行。
(1)负载惯量JW(负载折算到丝杠上的惯量[4])
(2)丝杠惯量J丝(丝杠折算到进给伺服电机上的惯量)
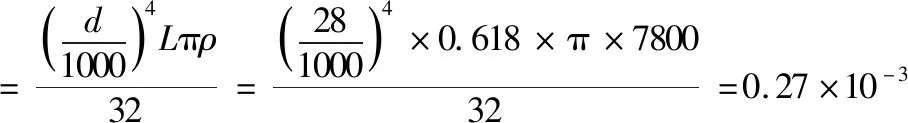
(3)X轴总惯量J总(移动部件折算到进给伺服电机上的惯量)
J总=(JW+J丝+J联)/i2=
(0.000 36+0.000 27+0.000 617)/12=0.12×10-3
(4)惯量比

(5)X轴进给伺服电机惯量匹配小结
1)J电≥J总时,进给系统动态响应最好,不经济、成本上升;
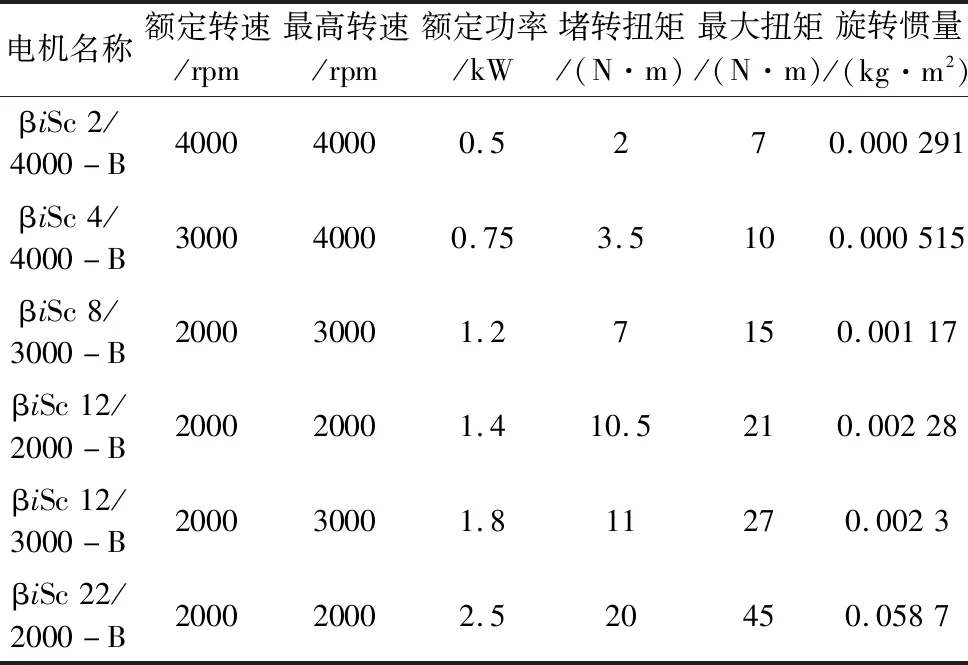
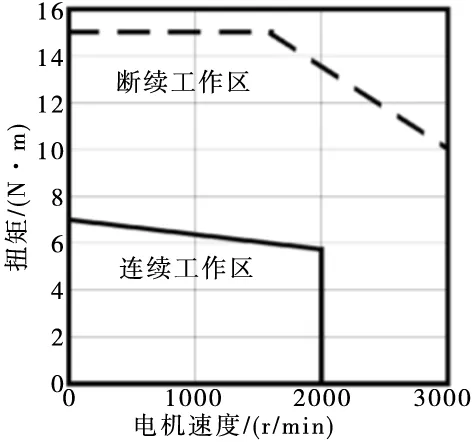
2)J电 3)4J电 4)负载惯量越小,进给系统动态响应越好。负载惯量越大,伺服电机规格越大,系统的时间增益越大,响应慢,会使系统的固有频率下降[5-6],易产生谐振,因而限制了伺服带宽,影响了伺服精度和响应速度。伺服电机惯量的适当增大只有在改善低速爬行时有利[7],因此,设计时在不影响移动部件刚度的条件下[8],应尽量减小负载惯量。 扭矩对进给系统的空载、切削、加速都有影响,是伺服电机重要特征参数之一[9]。针对普通数控车床而言,空载对进给伺服电机的扭矩要求比切削对进给伺服电机的扭矩的要求要大很多,如果是高速模具类加工车床,在考虑进给伺服电机扭矩匹配问题时,车床的加速度就要考虑进去了,因为加工时为高速曲线切削,对车床的加速度有较高要求[10]。设计时应使移动部件的扭矩需和进给伺服电机的峰值扭矩相匹配才行。 (1)X轴主切削力FY(可按钢件进行估算,刀宽b=5 mm、进给量s=0.1 mm/r) FY=2500bs=2500×5×0.1=1250 N; FX=0.55FY=0.55×1250=687.5 N;(X轴切削分力) FZ=0×FY=0×1250=0 N;(Z轴切削分力) (2)X轴负载动摩擦力F摩、下滑力F下、空载力F空 F摩=cosθWgμ=cos45×220×9.8×0.02=30 N; F下=sinθWg=sin45×220×9.8=1525 N; F空=F摩+F下=30+1525=1555 N; (3)伺服电机最高转数nmax、加速度α(t=0.11 s,数控车床一般为100~300 ms[11]) (4)匀速空载丝杠的载荷F匀空、匀速切削丝杠的载荷F匀切 F匀空=F空=1555 N; F匀切=F匀空+FX+FYμ=1555+687.5+1250×0.02=2268 N; (5)匀速空载、切削丝杠的载荷最大值Fmax Fmax=F匀切=2268 N; (6)匀速空载扭矩T匀空、匀速切削扭矩T匀切 (7)螺母预紧力Fp、螺母预紧附加摩擦扭矩Tp Fp=Fmax/3=2268/3=756 N; (8)丝杠预拉伸力Ft、轴承最大轴向载荷Fbmax、轴承预紧力Fbp、轴承启动附加摩擦扭矩Tb Ft=1.95Δtd02=1.95×3×22.42=2935 N;(Δt取2°C~3°C) Fbmax=Ft+Fmax=2935+2268=5203 N; Fbp=Fbmax/3=5203/3=1734 N; (9)最大加速扭矩Tmax (10)最大加速启动扭矩T空 T空=Tmax+T匀空+Tp+Tb=3+2.1+0.1+0.2=5.4 N·m; (11)最大加速切削扭矩T切 T切=Tmax+T匀切+Tp+Tb=3+3+0.1+0.2=6.3 N·m; (12)所需伺服理论峰值扭矩 15 N·m>6.3 N·m>5.4 N·m;(βiSc 8/3000-B进给伺服电机) 由表1、图2可以看出若选择βiSc 4/4000-B进给伺服电机,则最高转速4000 rpm>2500 rpm,满足;最大扭矩10 N·m>6.3 N·m,满足;但是堵转扭矩3.5 N·m<5.4 N·m,不满足;所以只能选择βiSc 8/3000-B进给伺服电机。 表1 FANUC公司进给伺服电机参数表 图2 FANUC公司进给伺服电机速度扭矩图 (13)X轴进给伺服电机扭矩匹配小结 通过以上计算过程,如果选取的伺服电机的峰值扭矩与移动部件最大加速启动扭矩、最大加速切削扭矩不匹配时,根据(6)中公式可以看出有3种优化方法。 1)重新选取扭矩大一规格的伺服电机,这种方法最简单,但不经济、成本上升; 2)传动比i不变,减小丝杠导程Ph,这样要按照(3)中公式重新选取伺服电机最高转数、加速度,直联车床按此优化; 3)丝杠导程Ph不变,增大传动比i,增大传动比对于降低负载惯量也是有利的,非直联车床按此优化。 Z轴进给伺服电机惯量扭矩匹配计算时注意以下几个公式变化: 第(1)中公式为:FX=0.7FY;FZ=0.6FY;第(2)中公式为:F摩=(sinθ+cosθ)·W·g·μ;F下=0;F空=F摩;第(4)中公式为:F匀空=F空;F匀切=F匀空+FZ+(FX+FY)·μ;其余计算公式同理X轴,本文不再详细计算。 本文通过新型全机能数控车床设计实例的形式,从伺服电机的惯量扭矩匹配两个方面系统地介绍了伺服电机惯量扭矩的计算过程、计算方法以及相应的调整、优化方法。希望能对数控车床设计人员提供一定的帮助并快速选型。3 X轴进给伺服电机扭矩匹配
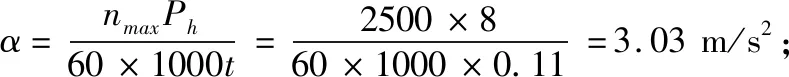
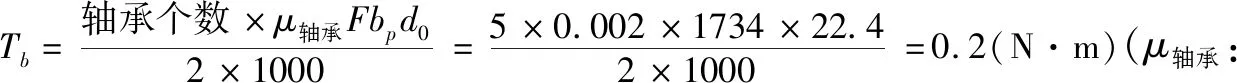
4 结束语

