基于BP神经网络的测功机温度补偿方法设计

张 威，张力平，周 浩

（长安大学道路施工技术与设备教育部重点实验室，西安 710064）

0 引言

近年来，新能源汽车的快速发展，对汽车的性能检测要求也越来越高，因此，对于测功机的性能研究具有很高的价值。电力测功机是针对各种动力机械进行性能测试的综合测试设备[1]。测功机系统的主要工作原理是依靠逆变器将电能转换成电机转子的机械能，然后通过对拖的方式将负载施加在被测电机上，从而模拟出被测电机在实际工况下的负载情况。永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）作为测功机系统的核心部分，由于其自身的结构，其参数很容易受到电动机运行过程温度等变化的影响，特别是在负载较大时，电动机的散热条件在某些工作条件下相对较差，电机的定子绕组会产生大量热量，导致电机腔内温度升高，严重影响电机永磁体磁链的大小以及定子绕组阻值，从而导致电机的实际输出转矩发生波动。近些年，国内外学研究学者对永磁同步电机各参数大多都进行各种有限元分析。王淑旺等[2-3]分析了电机运行过程中线圈绕组阻值随温度变化的情况，估算了温度升高对于PMSM磁链和转矩的影响。Han X等、林康和李统[4-6]分析了电机控制策略和热效应的损耗与瞬态温升的对应关系；瞬态温升分析结果表明电机工作时间较短时，绕组温度高于永磁体温度，但在长时间工作时，两者相差不大。Łukasz Knypiński等[7]采用气隙等效导热系数处理定转子间的热交换问题，给出三相定子绕组的等效热模型。

本文以额定功率为7.5 kW 的永磁同步电机测功机为研究对象，首先基于MATLAB/Simulink搭建各模块仿真模型，建立经典PMSM的矢量控制系统，并在此基础上增加BP神经网络的温度补偿环节，以d、q轴电流信号和电机的实时温度作为神经网络的输入，对网络进行训练，输出电机转矩的补偿信号，进而对测功机控制系统进行仿真；最后搭建测功机用PMSM控制系统实验环境，进行验证。

1 PMSM永磁体剩磁与矫顽力变化分析

永磁同步电机的定子绕组以及永磁体材料受温度影响较大，温度的升高会使永磁体发生不可逆转的退磁现象，导致永磁体磁链减小以及定子绕组阻值增大，从而使得电机的输出转矩出现波动，所以在电机的控制过程中必须要将温度变化的因素考虑进去。本文使用Maxwell 2D 建立N40UH 永磁体模型，作为分析电机转子永磁体剩磁与矫顽力随温度变化基础。分别获取电机温度25～150 ℃的单相磁链仿真结果。图1 所示为25 ℃时电机永磁体的磁链分布图。剩磁Br和矫顽力Hc随温度T变化的关系如下。

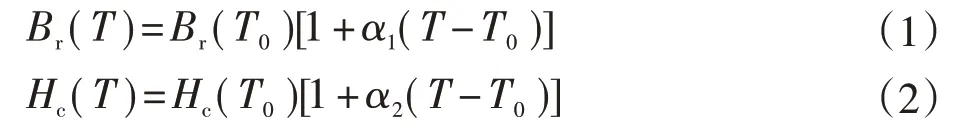
式中：T0为初始室温；α1和α2为温度系数，α1=-0.09%，α2=-0.5%；Br(T0)为永磁体剩磁初始值，Br(T0)=1.27 T；Hc(T0)为矫顽力初始值，Hc(T0)=939 kA/m。

图1 转子磁链分布图

取仿真数据中各个温度下的峰值就是电机永磁体磁链值，然后使用MATLAB 曲线拟合工具拟合得到永磁体磁链Ψf与温度T的函数表达式为：

式中：25 ℃≤T≤150 ℃。

根据电机定子绕组随温度变化的关系近似于线性关系，可得出定子绕组阻值R随温度T变化的关系表达式为：

式中：α为电机铜绕组的温度变化系数；R0为室温下定子阻值。

2 基于温度扰动的PMSM仿真分析及模型建立

由于传统的Simulink模型库中的PMSM电机模型是基于理想条件下的电机模型，而在实际情况下电机的定子绕组阻值、转子永磁体产生的磁链都会随着温度而发生改变，所以需要建立基于温度对电机的实际影响建立PMSM电机模型。通常永磁同步电机选取在d-q坐标系下建立电机模型。理想情况下，根据三相PMSM 结构特点可知，在d-q轴中，PMSM 电压方程为：

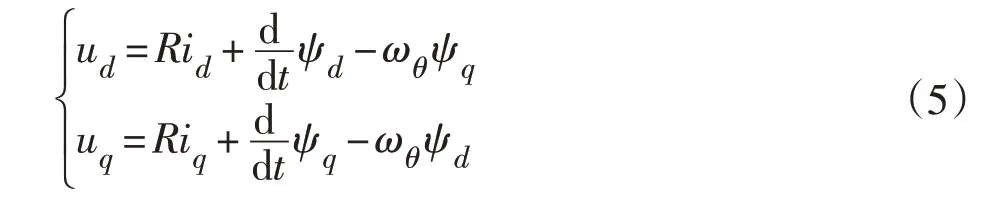
式中：ud、uq为电机d-q轴电压；id、iq为d-q轴电流；Ψd、Ψq为磁链在d-q轴上的投影标量；ωθ为电角速度。

磁链方程可表示为：

式中：Ψf为PMSM 转子永磁体产生的磁链；Ld、Lq为d-q轴上的电感分量。

将式（3）和式（4）代入式（5）中，可得带温度扰动的PMSM在d-q轴中的数学模型为：

对上式进行变化，得：

PMSM电磁转矩方程可表示为：

式中：Ψf、is分别为磁链以及定子电流矢量。

在d-q坐标系下，则有：

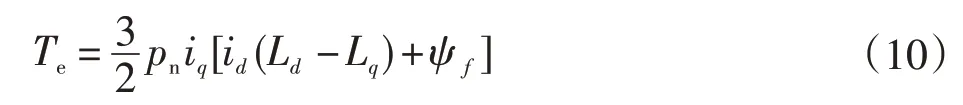
PMSM机械运动方程可表示为：

式中：ωm为机械角速度，rad/s，并且；Tl为负载转矩；J为转动惯量；B为系统阻尼。

在Simulink中根据式（3）和式（4）建立的输入为温度、输出为电机绕组阻值和永磁体磁链的仿真模型如图2所示。

在Simulink 中根据上述分析结合式（5）～（11）建立带温度扰动的PMSM电机模型。

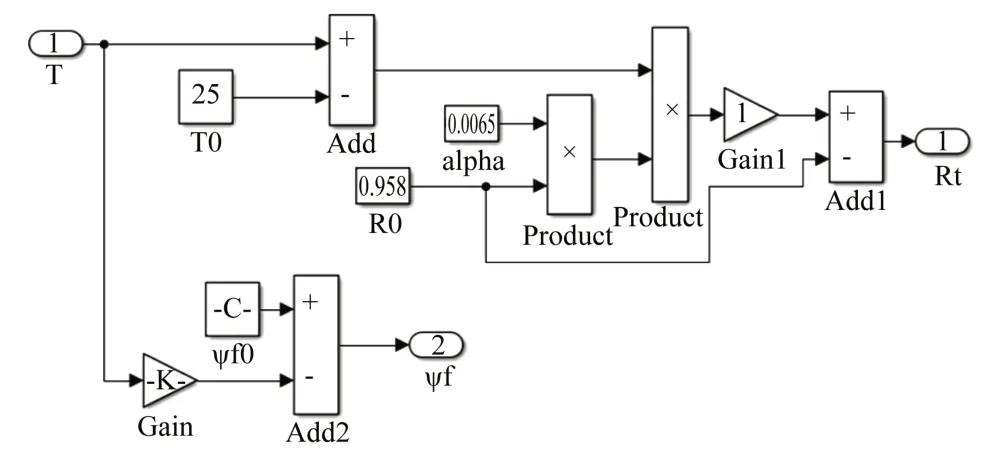
图2 绕组阻值随温度变化模型

3 基于BP 神经网络的PMSM 温度补偿系统仿真设计

在建立温度扰动的PMSM模型后，根据分析温度对PMSM 的影响，结合BP 神经网络建立温度补偿环节，将BP 神经网络模块用以补偿PMSM 电机转矩，减小电机实际转矩在运行时的波动值，基于BP神经网络温度补偿的PMSM模型原理如图3所示。

图3 PMSM温度补偿方案结构

为了得到含有温度影响的电流信号，首先，在转速环中将转速实际值与指令值比较，经过PI 调节器后输出的电流值再于实际电流及转换的电流补偿比较，这样得到的电流即为最终电流信号。将实际的交轴与直轴电流以及电机的温度值作为BP 神经网络的输入，根据转矩与交轴电流值的关系，可以用交轴电流值作为BP神经网络的输出，也就得到了转矩的补偿值。

4 仿真结果分析与实验论证

电机及系统控制参数设置为：逆变器电压Udc=72 V，目标转速500 r/min，极对数Pn=4，定子电阻R=0.958 Ω，电感Ld=5.25 mH，Lq=12 mH，永磁体磁链Ψf=0.193 7 Wb。在目标转速下分别设置电机负载转矩为20 N∙m 和40 N∙m，检测并分析电机的实际输出转矩，电机输出转矩Te如图4所示。电机空载开始运行，转速由0 r/min 逐渐上升到500 r/min，开始时有一定的超调，但调制过程很快结束，并进入平稳状态，此时电机电流与输出转矩都为零。负载增加后，电机负载突变，在加入了温度补偿环节后，电机实际输出转矩随温度升高下降的趋势明显变缓。如图所示，当电机的额定负载转矩为20 N∙m时，系统运行稳定后电机没有温度补偿的实际输出转矩由20 N∙m 下降到了17.68 N∙m，转矩值降低了2.32 N∙m，而加入BP 神经网络的温度补偿实际输出转矩由20 N∙m 下降到了19.36 N∙m，转矩值降低了0.64 N∙m。电机实际输出转矩下降百分比分别为11.6%和3.2%。而当电机额定负载转矩为40 N∙m 时，系统运行稳定后电机没有温度补偿的实际输出转矩由40 N∙m 下降到了36.44 N∙m，转矩值降低了3.56 N∙m，而加入BP 神经网络的温度补偿实际输出转矩由40 N∙m 下降到了38.71 N∙m，转矩值降低1.29 N∙m。电机实际输出转矩下降百分比分别为8.9%和3.223%。

图4 电机输出转矩Te

仿真结果表明，PMSM 在加入BP 神经网络温度补偿后，可以有效地对输出转矩进行补偿。

本实验所使用PMSM额定功率为7.5 kW，驱动电压为72 V。图5 所示为电机以及测功机台架实物图。测功机通过联轴器与被测电机进行连接，固定转速下通过PID调节器的输出值对被测电机施加负载，扭矩传感器通过CAN 总线连接到功率分析仪，可以将转矩值实时上传到上位机。

图5 测功机台架

电机输出转矩如图6所示，由图可以看出，在没有增加电机温度补偿环节情况下，在系统运行开始一段时间内，电机输出转矩基本保持不变，但是随着电机温度上升，转矩开始出现下降趋势，最终当电机运行80 min 后，电机输出转矩下降到9.53 N∙m，电机转矩下降了1.97 N∙m，相比于额定负载转矩，电机转矩下降百分数：

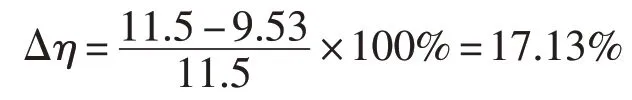
经过实验平台验证，证明了测功机用PMSM加入BP神经网络做温度补偿设计的可行性。

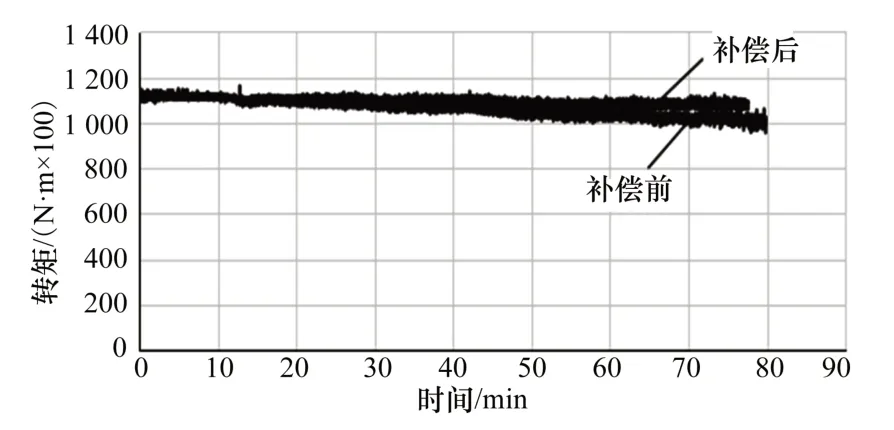
图6 电机输出转矩

5 结束语

本文基于温度补偿的PMSM 模型提出了利用BP神经网络构建前馈闭环网络对电机运行过程中由于温度变化而损失的转矩给与补偿。仿真及实验均表明该温度补偿方法的有效性。本文的仿真结果也可以看出，加入了温度补偿环节后电机的输出转矩仍然有很多的损失，为使得补偿效果进一步提高，还需对该方法进行深入分析，增加转矩补偿的精度。