基于有限元方法的行星轮系接触强度分析与研究

孔祥振，邹 雯

（1.枣庄科技职业学院，山东枣庄 277599；2.滕州市职业教育中心学校，山东枣庄 277599）

0 引言

行星轮系在机械装备中有着重要的应用，比如液粘软启动设备，通过不同齿轮系的相互协作，实现不同传动力矩和转速的控制[1]。行星轮系具有较高的可靠性，其功能优化和安全性提升也是国内外学者重要的研究对象[2-4]。在液粘软启动设备中的行星轮系中，斜齿轮副和锥齿轮副往往是容易发生损坏的机构，因此需要保证较高的机械强度。传统的机械强度校核只能保证总体的安全系数，对于结构的响应特性无法查看。针对以上问题，本文提出基于有限元方法对行星轮系的齿轮接触特性进行研究，通过有限元[5]分析软件ANSYS 计算强度和变形特性，为后续的结构优化提供重要依据。

1 有限元方法的应用

由有限元分析的基本原理可知，有限元方法可有效地解决非线性方程不容易求解的问题，在工程上有着较为广泛的应用，认可度非常高。目前，AN⁃SYS是有限元领域内使用最多的软件之一，其将分析过程分成3 部分：建模与前处理、迭代计算、后处理。在ANSYS 软件中，提供了诸多网格划分方法，用户能够根据自身需求选择合理的网格类型和尺寸。为了进一步提升模型计算精度，在网格初步划分完成后，还能够局部进行细化和优化，不但能够保证收敛性[6]，还能提升计算效率。对于复杂的模型，可以采用自适应网格划分方法。虽然六面体网格计算效率高，但如果不规则结构强制划分成六面体网格，会导致网格畸变程度过高，导致计算结果不可信。除了完成结构分析，ANSYS 还能完成其他物理场的计算，比如温度场分析、电磁场分析、声场分析等。并且，模型可根据物理场的交互效应进行不同耦合场[7]的计算，使得边界条件更符合真实条件。

在模型建立方面，需要定义和构建的内容有网格单元类型的选择、材料属性的定义与分配、几何参数的修正（略去对分析影响不大的结构）等。某些情况下，需要考虑材料的非线性特性，选择合理的函数关系，模拟实际的工况问题。软件中集成了建模模块，可直接进行参数化模型的构建，同时，也提供了主流的接口，能够识别几乎所有的中间格式模型。求解模块则为用户提供了载荷与边界条件的施加方法以及步骤，并通过模块化的方法集成了多种分析类型，比如静态分析、瞬态分析、谐波分析、模态分析、谱分析和挠度字结构等。后处理模型可有效地将计算结果以云图或者曲线的形式表达出来。根据以上分析可知，有限元分析方法在行星轮系的分析中可获得良好的应用效果。

2 斜齿轮副有限元分析

2.1 模型建立

根据行星轮系的结构可知，各个齿轮结构形状复杂，如采用ANSYS 集成的建模方法费事费力，因此，本文基于UG软件建立齿轮副模型，去除对结构影响不大的倒角，并将模型进行分块处理，如图1所示。为提高计算效率，取斜齿轮副的局部结构，通过中间格式iges导入ANSYS软件，进行静态结构分析。

图1 斜齿轮副三维模型

图2 斜齿轮副网格划分结果

根据分析目标，模型采用solid164单元类型进行网格划分，通过局部细化和优化后，得出网格划分结果如图2所示。然后，依次进行材料属性参数的设定，包括密度、泊松比和弹性模量。

2.2 结果分析

根据液粘软启动设备的驱动功率，计算出对主动轮（小齿轮）需要定义和加载的力矩为840 N·m。此时，设定从动轮与主动轮之间为有摩擦接触，定义接触面的接触属性。通过连续的迭代运算，最终可得出斜齿轮副的接触应力云图如图3所示，斜齿轮副应变云图如图4所示。

从图3～4 中可以看出：当承受较大的力矩载荷时，齿根处将产生较大的剪应力，而齿轮的最大变形位置在齿顶处。由于在特定传动比条件下，行星轮系的齿轮模数与齿数是固定的，采样增大齿数的方式降低接触强度的方式是不可取的，由此可见，采用表面处理[8]的方式提升齿根和齿顶的硬度是改进齿轮副可靠性最有效的方法之一。

图3 斜齿轮副应力云图

图4 斜齿轮副应变云图

由于齿轮在啮合工作时，齿根和齿顶均受到周期性的疲劳应力载荷，随着工作时间的延续，非常容易出现疲劳损伤，表现为裂纹初生和扩展。此外，根据分析结果还可以得出结论，在不同的啮合位置条件下，最大弯曲疲劳应力和最大弯曲拉伸应力具有显著的差异性，这表明脉动循环应力是决定断裂损伤主要因素。

3 锥齿轮副的有限元分析

3.1 锥齿轮副建模

锥齿轮副的主要作用为轴向变相，为得出其接触响应特性，建立整体的锥齿轮模型，在ANSYS/Workbench模块中对其进行网格划分，通过自适应网格划分方法，得出总体的网格结构，如图5所示。根据斜齿轮副分析结果可知，齿根和齿顶是最大承重区域，因此，采用局部表面网格细化的方法对接触区网格进行细化，得出网格如图6所示。

图5 锥齿轮副总体网格划分结果

图6 网格细化结果

3.2 结果分析

在锥齿轮系的承载方面，根据传动轴的额定载荷，设定齿轮的扭矩为33 369 N·m，加载位置为齿轮啮合线处。由于长期啮合工作后，机械损伤均发生在小齿轮，因此，为提升计算效率，将大齿轮刚性化。通过连续的迭代运算，可得出锥齿轮副应变云图如图7所示。从图中可以看出，锥齿轮的变形随着径向尺寸的增大而增大，最大承载位置在锥齿轮副相接触的啮合线处，其最大应变值为0.19，最大弯曲应力值为336.8 MPa，与理论计算值较为匹配。从分析结果看，对小锥齿轮的齿顶进行强化处理具有良好的经济效益。

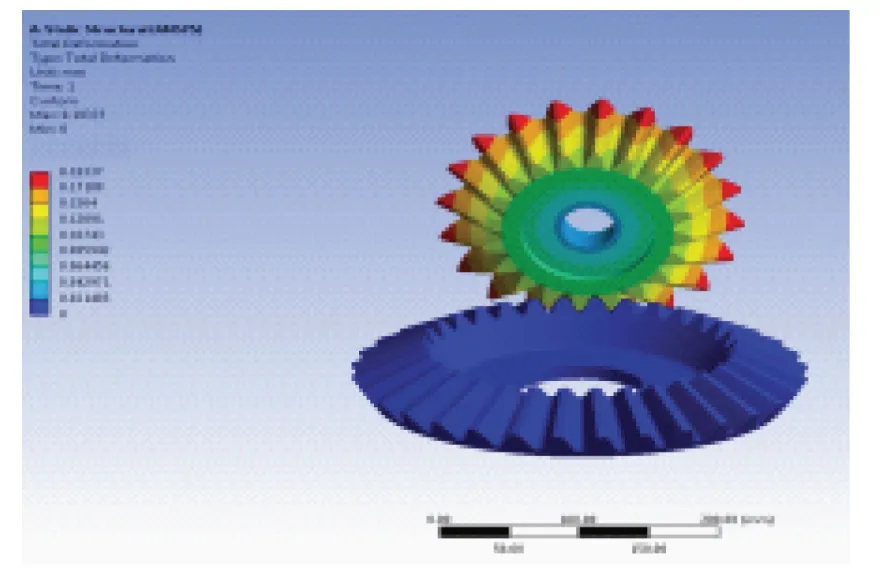
图7 锥齿轮副应变云图

4 结束语

有限元方法在机械工程领域的研究有着良好的应用效果，对于机械传动的可靠性与安全性有着重要的作用。斜齿轮副与锥齿轮副是行星轮系的关键组成部分，合理的强化手段不但能够提升经济效益，而且延长使用寿命，提升产品的市场竞争力。基于有限元方法的齿轮接触特性分析，可为齿轮的局部优化提供可靠和重要的依据，确保机械装备的安全性和可靠性，具有良好的经济效益和社会效益。