直流电机无差调速系统的MATLAB仿真

南昌航空大学科技学院 查竞舟

直流电机具有良好调速性能，而开环调速系统在负载变化时转速降较大，机械特性变软。可采用转速闭环控制减小转速降落、静差率，提高机械特性硬度。转速单闭环直流调速系统是一个有差系统，为了达到转速无差调节的目的，采用动态数学模型进行建模，并在Matlab/Simulink平台搭建直流电机调速控制系统，选择PI控制算法进行无静差调速系统的仿真实验。同时，给出转速、电磁转矩的波形，仿真波形表明，基于动态数学模型的单闭环直流电机调速系统能够实现无静差调速要求，并具备较强的抗扰能力。

1 无静差转速单闭环直流调速系统建模与仿真

构建调速系统仿真模型的基本思路是得到系统各环节的传递函数，然后在Simulink中利用相关模块实现，转速单闭环直流调速系统的仿真模型中应包含给定信号、比较环节、ASR(转速调节器)、PWM整流环节（用一阶惯性环节替代）、直流电机模块（图2）以及转速反馈环节，其中ASR使用PI调节控制。

给定信号模块用阶跃输入模块表示，Step time参数修改为0，Final Value设定为10V；ASR采用PI控制，用Gain模块表示，放大系数设定为7.85；UPE环节用一个一阶惯性环节表示，其中Ks=107.6，Ts=0.000125s；直流电动机环节为一子系统；忽略测速发电机的非线性因素，转速反馈模块亦可用线性模块Gain表示，放大系数为0.00383。整个系统的仿真模型见图1所示。其中直流电机环节为封装后的子系统模块，其内部仿真模型见图2所示。

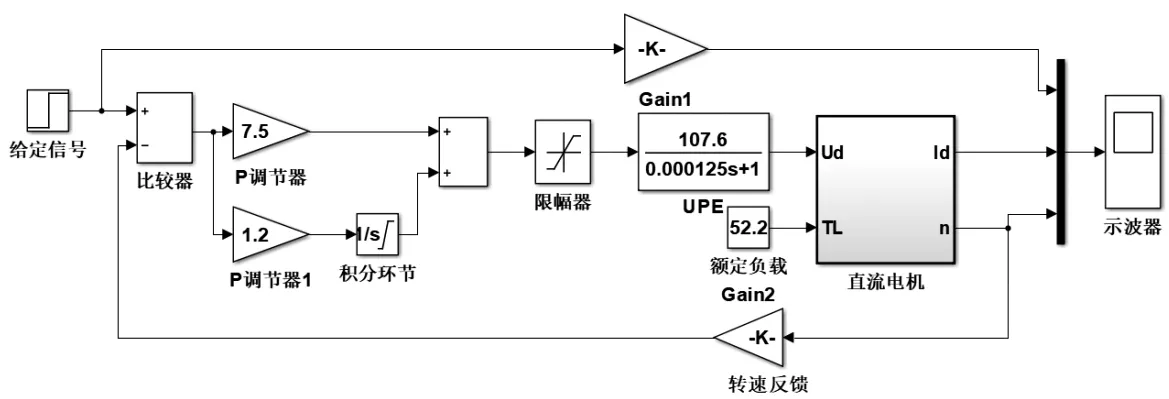
图1 无静差转速单闭环直流调速系统仿真模型

在图2中，为了便于观测调试，可以在适当的地方加入示波器模块，仿真中所选择的算法为ode23t，Start time设定为0，Stop time设为3，采用变步长仿真，最大仿真步长不宜过大，可设定为1e-5。

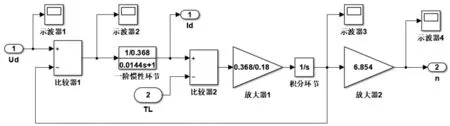
图2 直流电动机内部子系统仿真模型

2 系统仿真结果分析

仿真算法为ode23t，Start time设定为0，Stop time设为3，采用变步长仿真。可利用凑试法确定PI参数，经调试，选择Kp=7.5，KI=1.2进行仿真时的电流、转速响应曲线效果较好，波形如图3所示。由波形可知，电动机启动后转速快速上升，电流迅速增大，随着转速上升，电流又开始减小，经过PI调节后，电流降至额定电流52.2A，转速稳定在2610r/min，基本实现无静差调速。但是，本文所采取的仿真模型并未对电流采取限制措施，在起动过程中，电流的最大值超过1000A，远超过电动机的额定电流52.2A，这是绝对不允许的。解决的方法一是在图1的仿真模型中，引入电流截止负反馈；二是构建转速、电流双闭环控制的直流调速系统，读者可以参考相关文献。

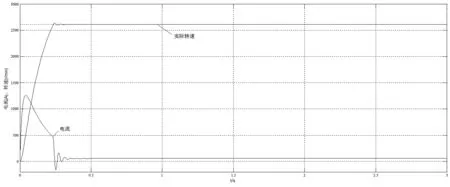
图3 Kp=7.5，KI =1.2时的给定、电流和转速响应曲线

3 负载变化时仿真结果分析

当其他参数不变，仅将负载在1.5s时刻从52.2A突变为200A，负载增加近4倍时系统的电流、转速响应曲线如图4所示，由波形图可知，尽管在t=1.5s时刻，负载增大，但经过短暂的调节后，稳态时的转速几乎没有变化，表明该系统具有较强的抗扰动能力。

图4 负载变化时无差调速系统的电流、转速响应曲线

本文利用动态数学模型建模法，将转速单闭环直流调速系统中的UPE电力电子变换装置、直流电机元件分别用相应的传递函数表示，然后在MATLAB/Simulink中利用相应的模块或者组合加以实现，这样省去了对电力电子主电路、电动机电路的搭建，使调速系统的建模更加简便。同时，分别对有静差和无静差直流调速系统进行了仿真，并给出了详细的仿真波形。仿真结果表明，基于动态数学模型的转速单闭环直流调速系统，ASR采取PI控制规律时，可以实现转速无静差调速，并且具有较强的抗扰能力，在实际生产中，具有一定的应用价值。