PSO-BP的短期电力负荷预测

安徽理工大学 周 莉 张 珂

应对短期电力负荷预测需求的提高，本文提出了一种BP神经网络的粒子群优化方法（PSO-BP算法）。通过对某地区短期负荷样本开展预处理，构建了基于PSO-BP的电力负荷预测模型。由实验结果可知，PSO-BP模型预测收敛速度快，精密度有一定的提高，运行时间缩短。

1 背景

社会不断发展，用电量在增加，需求也在提高。为有效降低“发输变配”等过程损耗，要制定准确的发电计划并合理调度。在我们制定计划和提出方案时，准确的负荷预测能为其提供合理的参考依据。

短期负荷预测一般是猜测未来24H或几天的电力需求。在供电调度和供电规划需求量的提升下，短期电力负荷预测为其提供了重要保障。它也在传统电力系统和无管制电力系统的运行中起着关键作用，是电力系统经济可靠运行的有效工具。

常用的电力负荷预测方法如表1所示。

表1 常用电力负荷预测方法

在当前新型电力能源市场环境下，为了适应更加灵活多变的时代节奏。本文提出建立一种PSO-BP模型，利用粒子群多输入输出能以最快速度靠近最优解得特性，再混合BP神经网络算法建立模型。通过绘制MATLAB仿真模型，经仿真证明，此算法减小了对网络收敛性和学习效率的影响。将数据集带入该模型后，能提高收敛速度，误差降到了0.0947。

2 归一化处理

有时，不同的数据范围、格式和类型会导致错误。由此，为了保证数据的质量，在呈周期性的时间间隔内，剔除无效数据、非标准数据和错误数据对于在短期电力负荷预测的情况下显得尤为重要。所以第一步要对样本进行归一化处理。具体方法如下：

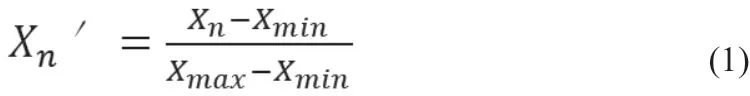
式中，Xn’为处理结果；Xn为样本电力数据；Xmax为样本最大值；Xmin为最小值。

处理完后数据的范围[0,1]。再反归一化操作，得到有量纲的预测数据：

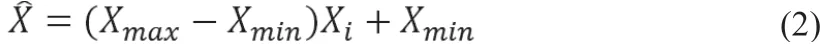
3 PSO-BP预测模型

3.1 BP神经网络基本原理

BP神经网络的概念在1986年被提出。它采用简单的三层网络，具体分为两个步骤：首先信号的前向传播，顺着输入到输出计算实际输出；再进行误差的后向传播，再逆方向校正权重和阈值。网络结构如图1所示。

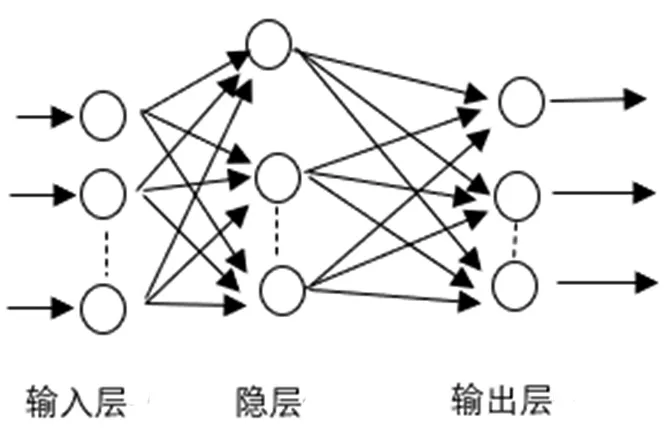
图1 BP网络结构图

3.2 粒子群算法

粒子群算法（Particle Swarm Optimization），是一种新型进化计算方法，它建立在鸟群聚集不断叠加最后定位于最佳觅食区域。PSO是一种迭代优化工具。D维空间中，量纲不变的情况下，初始化有Z个随机粒子组成一个粒子群体。假设其中第i个粒子的空间位置为Xi=(Xi1，Xi2，…，XiD)，(i=1，2，…，Z)，这个粒子的位置作为优化的一个潜在解。我们的目标就是不断更新这个位置，通过迭代找到“极值”。列出优化函数，将i粒子的位置代入，得到适应值，以此来判别Xi的好坏。经过第N代后，第i个粒子所经历过的位置作为历史最佳，记为Pi=(Pi1，Pi2，…，PiD)；同时其各自飞行速度为Vi=(Vi1，Vi2，…，ViD)；迭代结束后，粒子群的历史最佳位置记为Pg=(Pg1，Pg2，…，PgD)。每一代粒子，其第d维(1≤d≤D)的速度与位置迭代规律详见(1)、(2)所示。

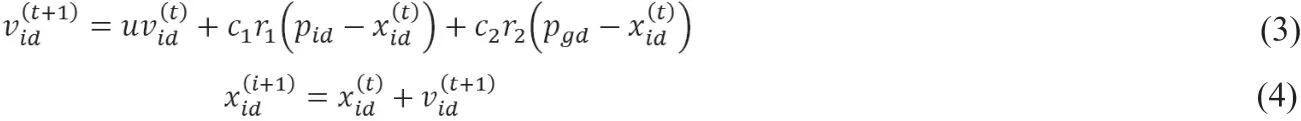
式中，u为惯性权值，代表部分寻优能力；c1和c2代表加速系数；r1和r2为随机数，在[0,1]内变化。

3.3 优化过程

计算BP网络的隐含层节点数，通常采用剪枝或分步构造法。在试行过程中，其个数会不停变化，初始权值和阈值也要更改，保持不对称性。由此，会让网络收敛性不稳定，学习效率变差。为了减小这种影响，本课题采用新方式，对每个网络都设定N个不同初始权值和阈值的BP网络，再采用PSO-BP算法进行优化。在初始化不同的网络中，经过算法训练，逻辑判断，最终得到的BP网络误差最小。优化过程如图2所示。

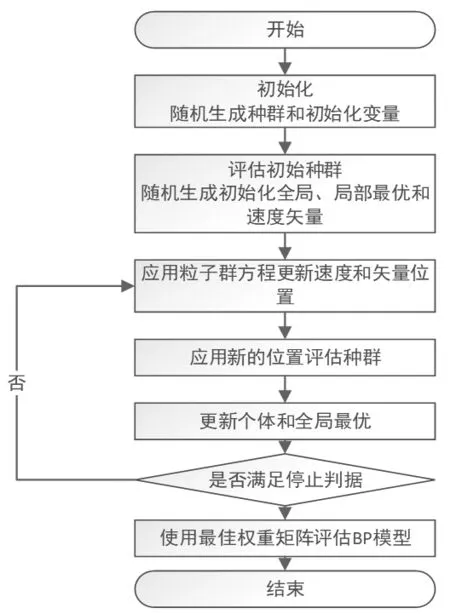
图2 PSO-BP算法流程图

4 实验部分

当外部影响因素大致相同时，在相同时间段内，因为短期负荷曲线的周期性和连续性的特点，负载变化趋向基本相同，峰谷负荷的时间基本一致。由此，本文利用某一地点每15min采样的电力负荷数据，经过预处理后，搭建模型，利用PSO-BP算法进行预测。预测原理如图3所示。

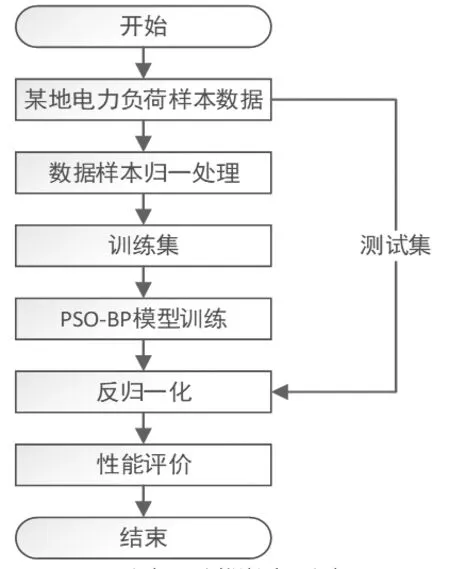
图3 预测原理图

本课题的仿真环境为MATLAB2020b，本课题采用某地的每15min采样的电力负荷数据建立预测模型。900个样本用以建立模型作为训练，100个作为检验。建立PSO-BP预测模型后，把样本代入预测电力负荷。通过对比PSO-BP和BP模型的均方误差（MSE）来评价模型优劣，结果如表2所示。

表2 均方误差对比

N个样本，X为真实值，X’为预测值。

通过比较两种预测模型结果，和BP神经网络预测模型对比，PSO-BP预测模型的均方差误差更小，能一定程度上改善收敛性能。从效果图来看，输入输出之间的映射能力有一定的提高，误差降低至0.0947。

把样本代入PSO-BP模型中实行电力负荷预测，得到模型预测效果曲线如图4所示。得到预测误差如图5所示。将样本代入BP神经网络模型中，得到对比图如图6所示。

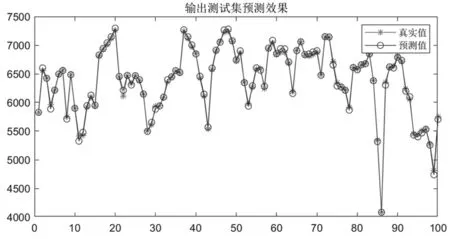
图4 输出测试集预测效果（PSO-BP）

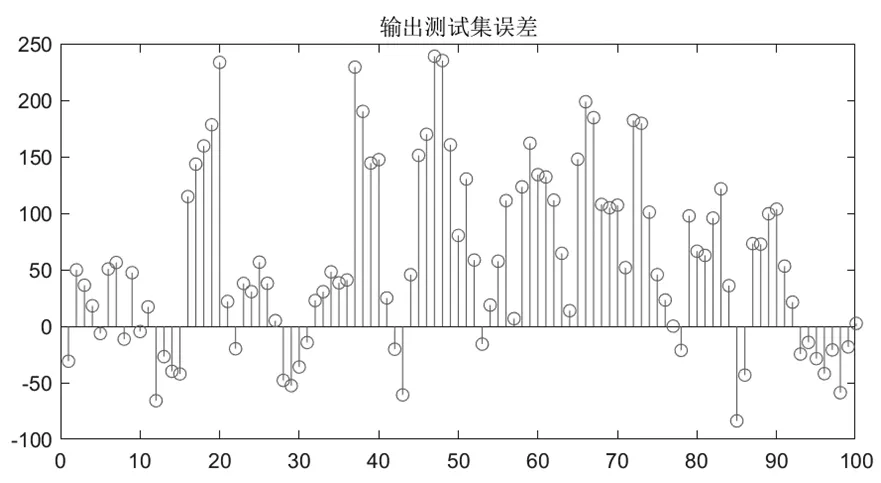
图5 输出测试集误差（PSO-BP）

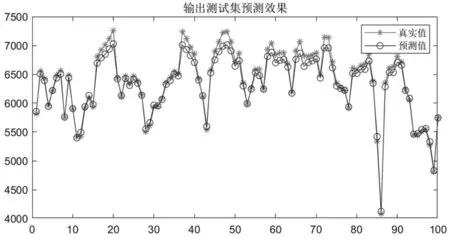
图6 输出测试集预测效果（BP）

结论：本课题采用PSO-BP算法和BP神经网络两种模型对同一地点的同一数据集进行预测。结果表明，与基本BP算法训练结果相比，粒子群多数入多输出优化BP网络的模型，一定程度上提高了学习能力，使试验不局限于单纯的网络结构。