应用可视化技术的配电房三维模型设计方法

2021-02-28 02:37任核权章剑光胡宇晴杨剑峰陈桂芳

电气自动化 2021年6期

任核权，章剑光，胡宇晴，杨剑峰，陈桂芳

(1.绍兴大明电力设计院有限公司，浙江绍兴 312000；2.国家电网绍兴电力局电力经济技术研究所，浙江绍兴 312000)

0 引言

随着国家大力推进智能电网的建设，需要建设配电房的数量也随之增加，如何提高配电房的建设效率和保证配电房的质量是目前智能电网建设需要解决的重点问题。文献[1]将三维可视化建模技术应用到矿山建设中，使用3DMine软件对矿山的地表模型、煤层模型以及巷道模型进行建模，并对巷道的可视化进行了设计。然后介绍了一种可视化模型的优化方法，提高模型的准确率，对矿山的建设具有一定的指导作用，但是对模型的优化效果不佳。文献[2]将三维可视化建模技术应用到城市地下管廊的建设中：首先介绍了城市地下管廊的建设和管理现状以及三维GIS和BIM技术的应用现状；然后采用了qt+vs2010+SQLite和Unity 3D软件设计了一个一体化建模地下管廊可视化建模系统；最后，以横琴新区中心北路地下管廊为例，对上述建模系统进行了验证，在城市地下管廊的管理和查询领域具有良好的应用前景，但是没有考虑到模型的优化，模式的准确率不高。

基于以上内容，本文首先采用三维激光扫描仪对现有的配电网进行实体扫描，对扫描得到的图像进行处理；然后采用3ds Max建模软件对配电房进行三维建模；最后为了提高模型的精度，采用最优最小生成树分别对模型的局部和全局进行优化，便于后续的分析和研究。

1 基于3ds Max的配电房建模方法

配电房的线路规划和一些电气设备的位置会影响配电网的运行，因此不断改进配电房的结构以及内部的规划对配电网的运行以及后续的维修具有一定的帮助[3]。本文通过三维可视化建模技术实现配电房场景的还原，采用3ds Max软件对现有的配电房进行建模，建模分为两个部分：三维激光扫描获取信息和3ds Max建模[4]。配电房的三维建模流程如图1所示。

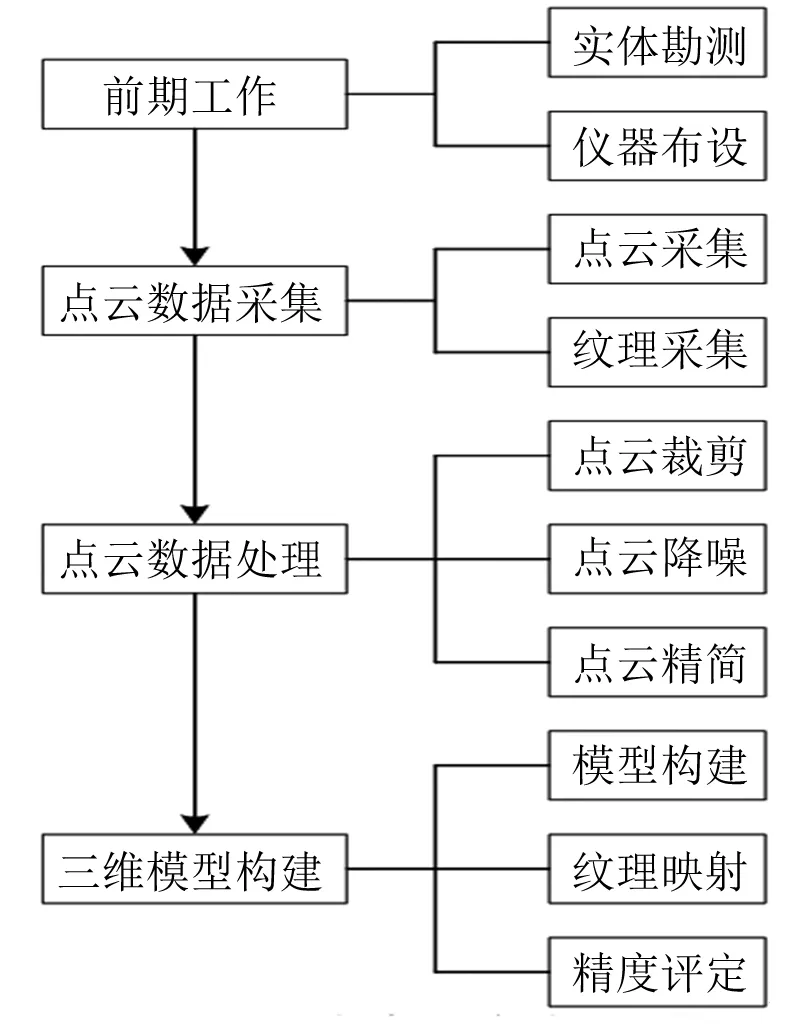
图1 配电房三维建模流程

模型的建立首先需要对三维激光点进行云建模。三维激光点的云建模首先需要对数据进行采集，本文使用的是徕卡公司的三维激光扫描仪[5]，对配电房内外部的结构以及设施进行扫描，进行多点位分析，能够得到三维激光点的纹理照片和云数据；然后对数据进行处理，即图像进行降噪、裁剪、精简和配准操作，得到符合3ds Max使用需要的图像和数据[6]。配准使用的是ICP算法，可以得到全面和坐标统一的点云数据，裁剪的目的是筛选出感兴趣的点云数据区域，对不感兴趣的区域进行剔除。

本文配电房的建模方式采用的是规则体建模方式，根据点云的轮廓，首先对配电房的主体完成建模。然后对建筑的细节以及内部的电器设备进行建模，得到较为完整的配电房模型。最后将使用三维激光扫描仪得到的纹理照片进行处理后与配电房的模型进行贴图，得到与配电房实物具有一定比例的配电房三维模型。

2 基于最优最小生成树的模型优化方法

最小生成树(MST)是一个数学模型，主要的用途是优化，因为其能够清晰地表现出模型的拓扑结构，在网络设计和数据挖掘领域具有广泛的应用。最小生成树的经典算法有Prim算法和Kruskal算法两种，本文构建初始的最小生成树使用的是Prim算法，因为Prim算法能够从任意顶点出发，不断地加入距离生成树顶点最近的模型顶点，多用于构建边稠密的生成树[7]，而配电房内部存在多种电气设备以及开关，因此使用Prim算法。

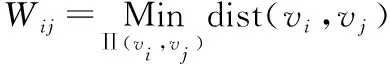
3D-MST

输入：加权连通图G(V,E)；

输出：模型3D-MST=MST(Vnew，Enew)。

BEGIN

(1)Vnew={vi}，Enew=∅

(2)WhileV-Vnew≠∅ do

(3) 在V-Vnew中选择一个vj使得Vnew中顶点vi的权值最小的边Eij

(4)Vnew←Vnew∪{vj}，Enew←Enew∪{Eij}

(5)return MST(Vnew，Enew)

END

虽然建模之前已经对图像进行了一定的降噪处理，得到的三维模型的精度已经不错，但是为了得到精度更高的图像。本文通过构建模型的最小生成树，对模型的局部和整体进行优化。

局部优化采用的是双边滤波，双边滤波在图像处理方面的应用已经比较成熟，具有非线性的特征，能够对图像进行保边降噪。滤波器由几何空间的距离测量函数和像素灰度的特征测量函数两个测量函数组成[8]。几何空间的距离测量函数对滤波系数d具有绝对性的影响，像素灰度的特征测量函数对滤波系数r具有绝对性的影响。像素的输出值主要取决于邻域像素值的加权值，计算公式为:

(1)

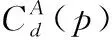
距离滤波系数的表达式为：

(2)

式中:W(i,j)为模型上vi、vj两点之间的测地线距离；σd为空间几何距离的标准差。

特征滤波系数的表达式为：

(3)

式中：Ti、Tj为顶点vi和vj的体积；σr为体积特征的标准差。

权重系数w=d×r也可以写成：

(4)

滤波后的特征为：

(5)

式中：ni为顶点vi一环邻域的顶点数目。

采用双边滤波方法优化图像的核心思想是通过测地线之间的距离来判断几何空间的差异性，将特征差异用体积特征来表示。通过滤波器对具有缺陷的特征进行过滤，保留相对完整和质量较好的特征。

全局优化采用的是信息熵，熵最初是热力学中的一个概念，主要用来表示气体分子的流动状态，而信息熵是由美国信息论的创始人香农提出的，将其用来表示信息量，信息熵的值越大则代表信息量越小。图像的检索和特征选择经过不断的发展，也引入了信息熵，但是信息熵只会对模型的整体特征进行表示，不能表示局部的特征。因此为了实现模型的全局优化，本文根据局部滤波的形状特征，结合模型的整体特征分布(信息熵)来进行处理。

具体的步骤如下：

(1) 将体积特征[min(T′),max(T′)]平均分成L个子区间，对每个区间内的顶点进行统计，记作ni(i=1,2,…,L)。

(2) 计算ni的概率分布P={p1,p2,…,pL}。

(6)

(3) 根据信息熵的计算原理，计算模型顶点的体积特征的信息熵H。

(7)

熵权值Ci表示区间为整个模型提供熵的量Di与整体熵H的比值。计算公式如下：

Di=-pi·lnpi

(8)

Ci=Di/H

(9)

进而计算区间顶点的熵权值为：

C(vi)=Ci/ni

(10)

(4) 全局优化的最后是通过步骤(3)得到熵权值和特征点，并将非特征点向特征点聚合，从而实现模型的全局优化。计算顶点的信息特征差值d：

d(vi,vj)=abs[C(vi)-C(vj)]

(11)

式中:vj为vi的子节点。

通过计算阈值γ，根据顶点的信息特征差值d与阈值γ的比较进行节点剔除，阈值γ的计算式为：

γ=φ·avg[d(vi,vj)]

(12)

式中:φ为阈值参数，用来控制阈值的大小。如果d≤γ，则删除子节点，保留父节点；如果d>γ，则节点全部保留。

模型的优化应该是局部优化在前，全局优化在后，保证模型优化的可行性。

3 试验与分析

在实验室即可完成对上述模型优化方法的仿真与验证。验证分为两个部分，采用优化和不采用优化的模型效果对比，采用最优最小生成树和不采用最优最小生成树的模型效果对比。首先对使用的计算机配置进行说明，操作系统为Windows 7，CPU为Inter Core i7-9700，运行内存为DDR4 3 200 MHz 16G，硬盘大小为1 TB[23]。

为了更直观地表现模型的质量，引入可视化体积指数和形状分布(SD)作为评估标准，可视化体积即人眼能看到的模型体积，两个评价指数都介于0～1之间，越大表示模型的质量越好。

首先采用上述建模方法对某实体配电房进行建模，建模完成后，采用章节2中的方法对模型进行优化，对优化前后的模型进行可视化体积和形状分布计算，得到表1的数据。

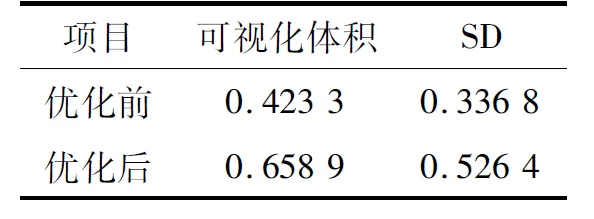
表1 模型对比

从表1可以看出，模型经过本文方法优化后，可视化体积和SD都有所提高。但是只有一次的试验并不能说明本文模型优化方法的可行性，依旧采用本文的三维建模方法和模型优化方法对五个不同的配电房进行建模和优化。为了更直观地表现优化前后的模型质量，采用图形的方式表达，可以得到图2所示的优化前后对比图。

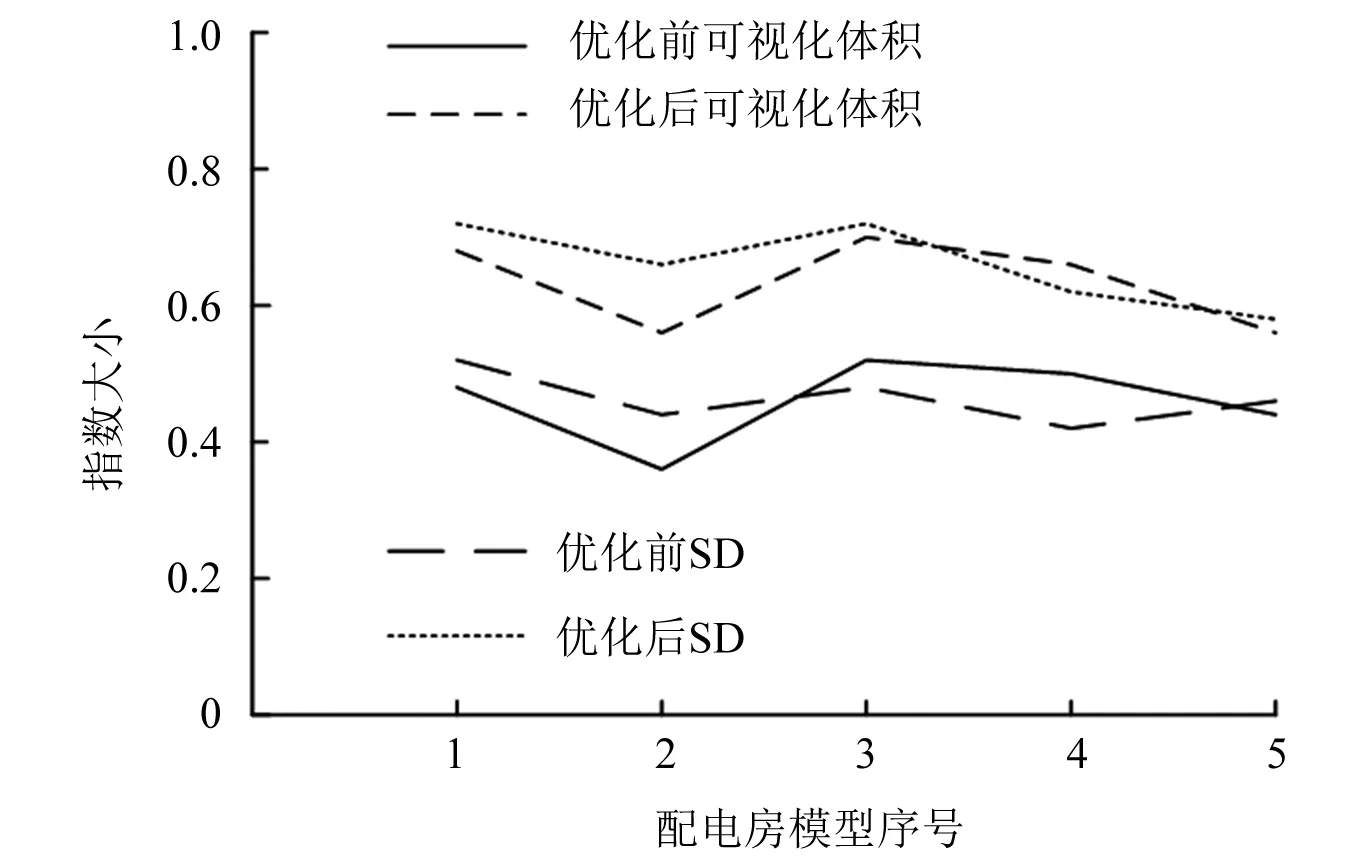
图2 优化前后的模型质量对比

通过图2可以看出，对于5个不同的配电房，通过本文方法进行建模和优化，优化后的可视化体积和SD都比优化前的高，说明本文的模型优化方法能够提高模型的质量，对后续的分析提供帮助。

本文模型优化的方法采用的是最优最小生成树。采用最优最小生成树与最小生成树两种方法进行对比验证。分别采用两种方法对建模完成后的配电房模型进行优化，计算两种优化方法得到一个模型的可视化体积和SD，对数据进行整理得到表2所示的对比数据。

表2 两种模型优化后的模型对比

从表2可以看出，采用最优最小生成树的模型优化方法得到的模型可视化体积和SD比采用最小生成树模型优化方法得到的模型高，即本文的最优最小生成树模型优化的效果要比采用最小生成树的优化效果要好。但是只进行了一次对比试验，无法有效地证明本文模型优化方法的先进性，因此进行了多组对比试验。采用直方图的形式反映5组对比试验的结果，如图3所示。

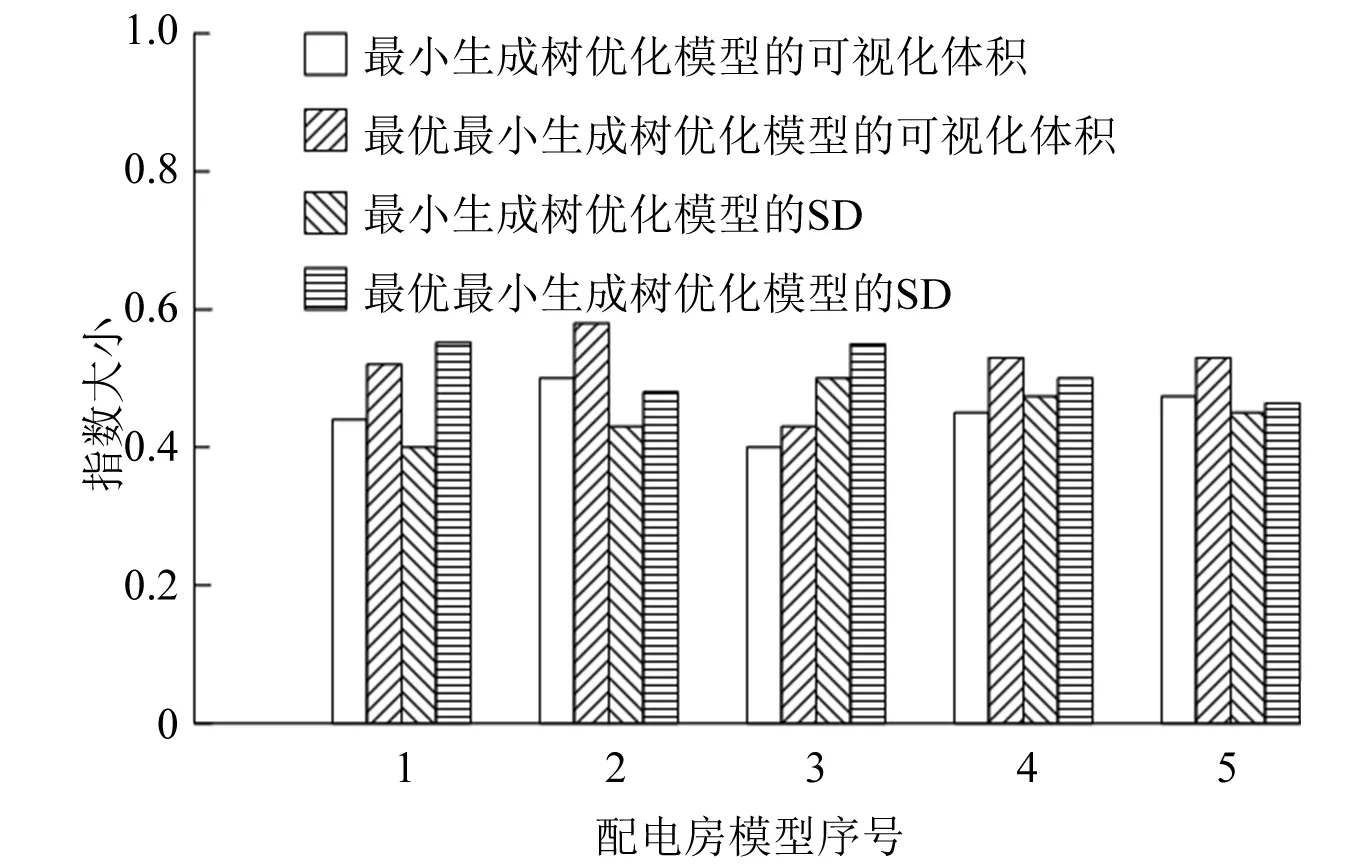
图3 两种优化方法的效果对比

从图3可以看出，5次的对比试验结果均采用最优最小生成树进行优化得到的模型可视化体和SD，比采用最小生成树进行优化得到的模型要高。虽然有些时间提高的不多，但是依然能够说明本文的模型优化的效果要更好。

综上所述，本文的三维模式建议和优化方法能够得到质量比较优秀的模型，对后续的分析提供技术支持。

4 结束语