基于改进鸡群算法的无功优化综合分析

郭堃， 薛太林， 耿杰， 杨擎宇， 张昊杰

(山西大学 电力工程系，山西 太原 030013)

0 引 言

鸡群算法(chicken swarm optimization，CSO)是Meng等人于2014年提出来的仿生优化算法。鸡群算法启发自鸡群觅食行为，与其他优化算法相比具有参数少、收敛速度快和收敛精度高的优点[1-3]。因传统的无功优化算法如梯度法、二次规划法等要求目标函数和约束条件尽可能可微、可导，对数学模型精度要求较高和对初始解要求苛刻，研究学者将人工智能算法应用到无功优化上[4]。

电力系统的无功优化问题因其拥有高维数、多变量和多约束的特点，在面对无功优化这样的高维问题时，鸡群算法易陷入局部最优[5]。因此，本文引入反向学习、柯西变异和学习因子来改进鸡群算法，提高算法的寻优能力，并与其他算法比较验证其有效性。

1 鸡群算法

鸡群算法由模拟鸡群的社会结构和觅食规则而来的群智能算法，即将整个群体分为公鸡、母鸡和小鸡三个群体。每个小组都是由公鸡、母鸡、鸡妈妈和小鸡组成，每个小组由公鸡带领进行觅食，组中小鸡只跟随鸡妈妈觅食。这种种群关系可以存在数代，数代后重新划分种群关系[6]。

位置更新规则如下：

(1) CSO中将适应度值高的定义为公鸡，其觅食能力高于母鸡和小鸡。公鸡的位置更新公式如式(1)所示。

(1)

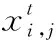
(2) 母鸡为适应度适中的个体。母鸡的觅食行为受到该子群中公鸡的影响，并且也会受其他群体中的公鸡母鸡的影响，但不会受到小鸡的影响，其位置更新公式如式(2)所示。

(2)

(3)

C2=exp(fr2-fi)

(4)

式中：Rand为0到1之间的随机数；C1为该母鸡所在子群的公鸡r1对该母鸡i的影响系数；C2为从全种群中随机选取的公鸡或母鸡r2对该母鸡的影响系数。

(3) 小鸡受鸡妈妈影响，跟随鸡妈妈进行觅食。位置更新公式如式(3)所示。

(5)

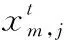
2 改进的鸡群算法

为了改进鸡群算法在面对无功优化这样的高维问题时，容易陷入局部最优的问题。本文从三个方面对鸡群算法进行改进。

2.1 反向学习

为提高算法的收敛速度，引入反向学习机制对种群初始化进行改进。即在计算每个个体的适应度值时，同时计算其反向个体的适应度值，并与该个体进行比较。若该个体的适应度值大于该反向个体，则选取该反向个体替代该个体来进行种群适应度值排序。反向个体的选取规则如下：

(6)

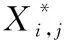
2.2 柯西变异

为解决母鸡容易陷入局部最优的问题，引入柯西算子来对母鸡进行变异。柯西分布函数具有中间峰值低，两边分布长的特点。一维柯西分布的概率密度函数为：

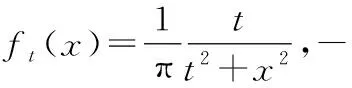
(7)

式中：t为比例参数且大于0。

本文对母鸡进行柯西变异，利用柯西分布中间峰值低的特点，使母鸡花费在局部最优的邻域内搜索的时间减少，让母鸡用更多的时间花费在全局最优的搜索上。使用柯西变异后的母鸡位置更新公式如下：

(8)

式中:C(0,1)为比例参数为1的柯西分布所产生的随机数。

2.3 学习因子

由于小鸡位置更新只与母鸡有关，当母鸡陷入局部最优时，小鸡不可避免也会陷入局部最优。为解决这个问题，引入学习因子，使小鸡跟随母鸡的同时也会与公鸡学习。引入学习因子的小鸡位置更新规则如下：

(9)

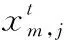
2.4 流程图

改进鸡群算法的具体流程为：

(1)初始化鸡群参数。确定鸡群总数X、公鸡数NG、母鸡数NM、鸡妈妈数NJ、小鸡数NC、最大迭代次数和更新代数G等基本参数。

(2)设置目标函数，迭代次数k=1。

(3)判断当前迭代次数是否是更新代数G的整数倍：若是则运用式(6)计算鸡群每个个体和其反向个体的适应度值，判断是否反向个体要替代该个体，然后对每个个体进行适应度排序，将鸡群分成若干子群，确定子群各个体之间的等级关系，然后按步骤(4)进行；否则直接按步骤(4)进行。

(4)按照式(1)、式(8)和式(9)来对公鸡、母鸡和小鸡进行位置更新。

(5)更新个体最优值和全局最优值。

(6)令k=k+1，判断是否满足最大迭代次数，若是则输出结果，否则转向步骤(3)。

对应的流程如图1所示。

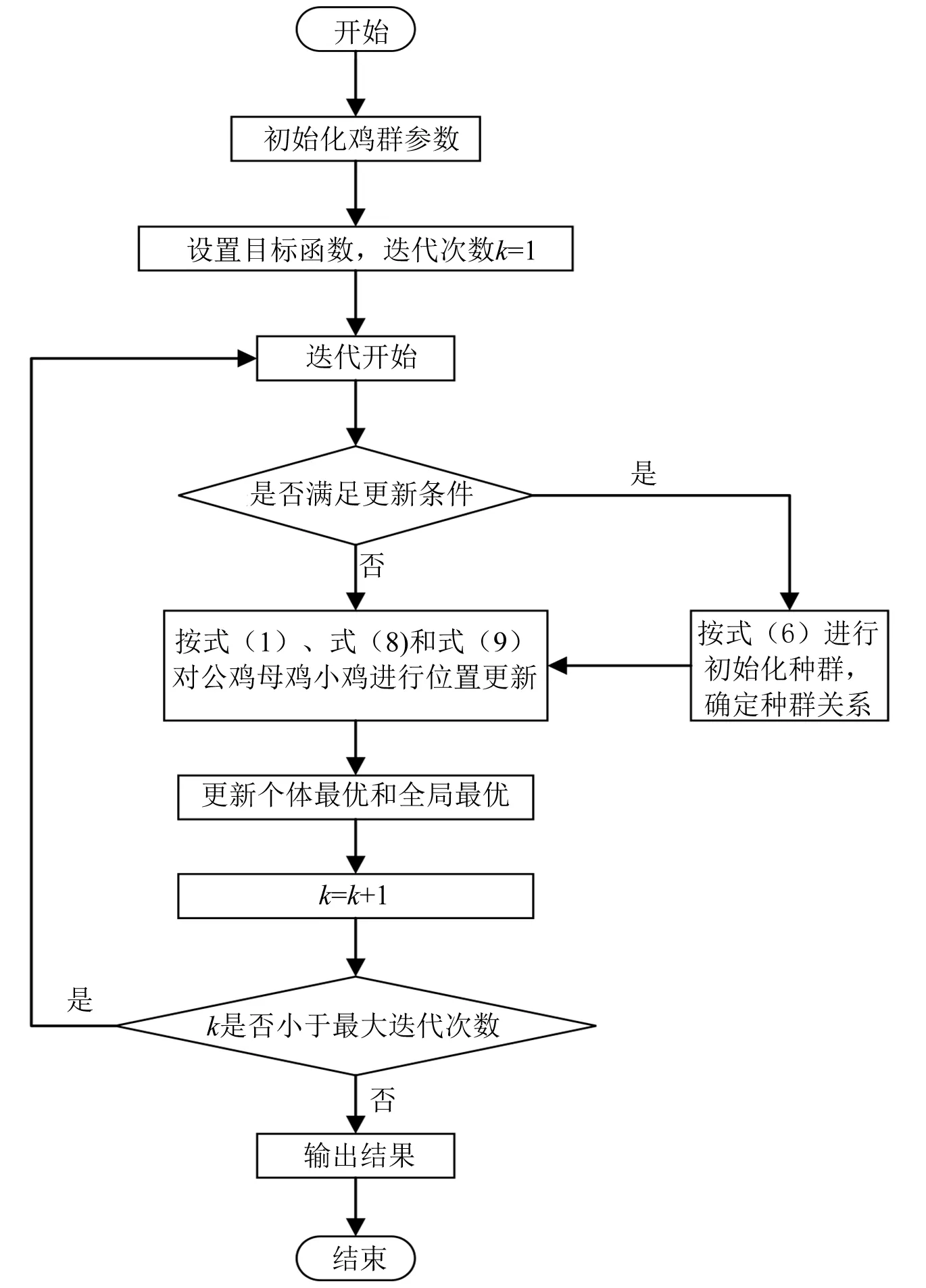
图1 改进鸡群算法流程图

3 无功优化数学模型

无功优化目标函数的建立通常考虑其经济性和安全性两方面。本文从经济性出发，以有功网损最小为目标函数，其表达是为：

(10)

式中:gij为电导纳系数；θij为节点i到节点j的电压角度之差；Ui、Uj为节点i、j的电压幅值。

4 算例分析

使用MATLAB编程对IEEE 30节点系统进行仿真。该系统6台发电机分别为节点1、2、5、8、11、13；2个无功补偿点分别为10、24；4台有载调压变压器为4-12，6-9,6-10,27-28；22个负荷节点。基准容量为100 MVA。节点接线图如图2所示。

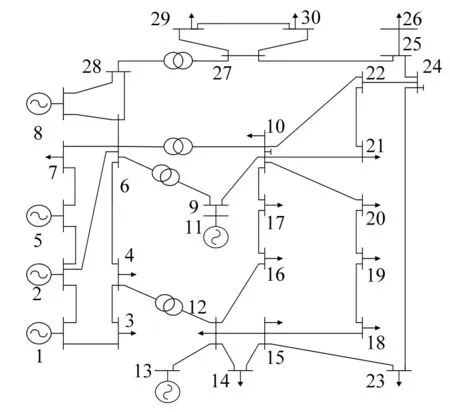
图2 IEEE-30节点接线图

参数设置：算法最大迭代数为100，种群数量为100，其中公鸡数为20，小鸡数为20，母鸡数为60，更新代数G为10，学习因子C为0.6。无功优化前让所有发电机电压取1.0，变压器变比取1.0，无功补偿容量取0，变压器变比上下限为0.9～1.1，步长为2.5%，无功补偿容量上下限为0～0.5，步长为0.1，系统的初始网损为0.078。

改进CSO、CSO、PSO、DE对上述目标函数求最优解，得出有功网损和网损降幅以及收敛时的迭代次数结果如表1所示。

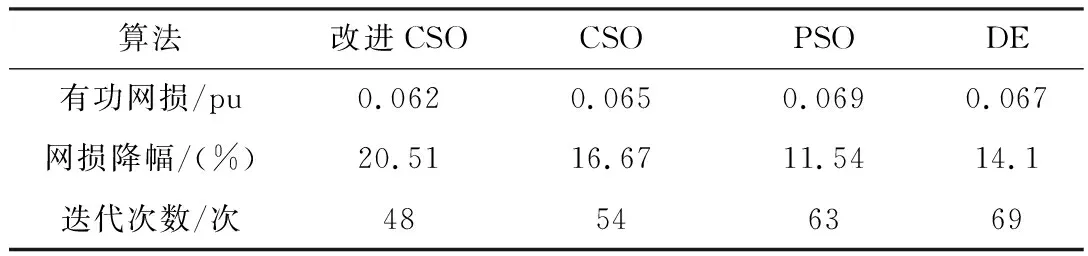
表1 4种算法算法的性能比较

从优化结果可以看出，通过对系统进行无功优化，改进CSO的优化效果均好于其算法，改进CSO与初始潮流相比，有功网损从0.078降低到了0.062，降低了20.51%。从表1可以看出，改进CSO算法的优化结果明显高于上述其他三种算法，说明了改进后的CSO算法跳出局部最优的能力大大加强。

在上述目标函数下，改进CSO、CSO、PSO、DE的收敛曲线如图3所示。

通过图3以及表1可以看出，改进CSO算法在迭代次数为48次时收敛，得到的最优值为0.062。改进CSO算法的收敛速度和收敛精度均高于其他算法，说明改进CSO算法跳出局部最优的能力大大加强，收敛速度得到提高。综上所述，可说明改进CSO算法的有效性和可行性。

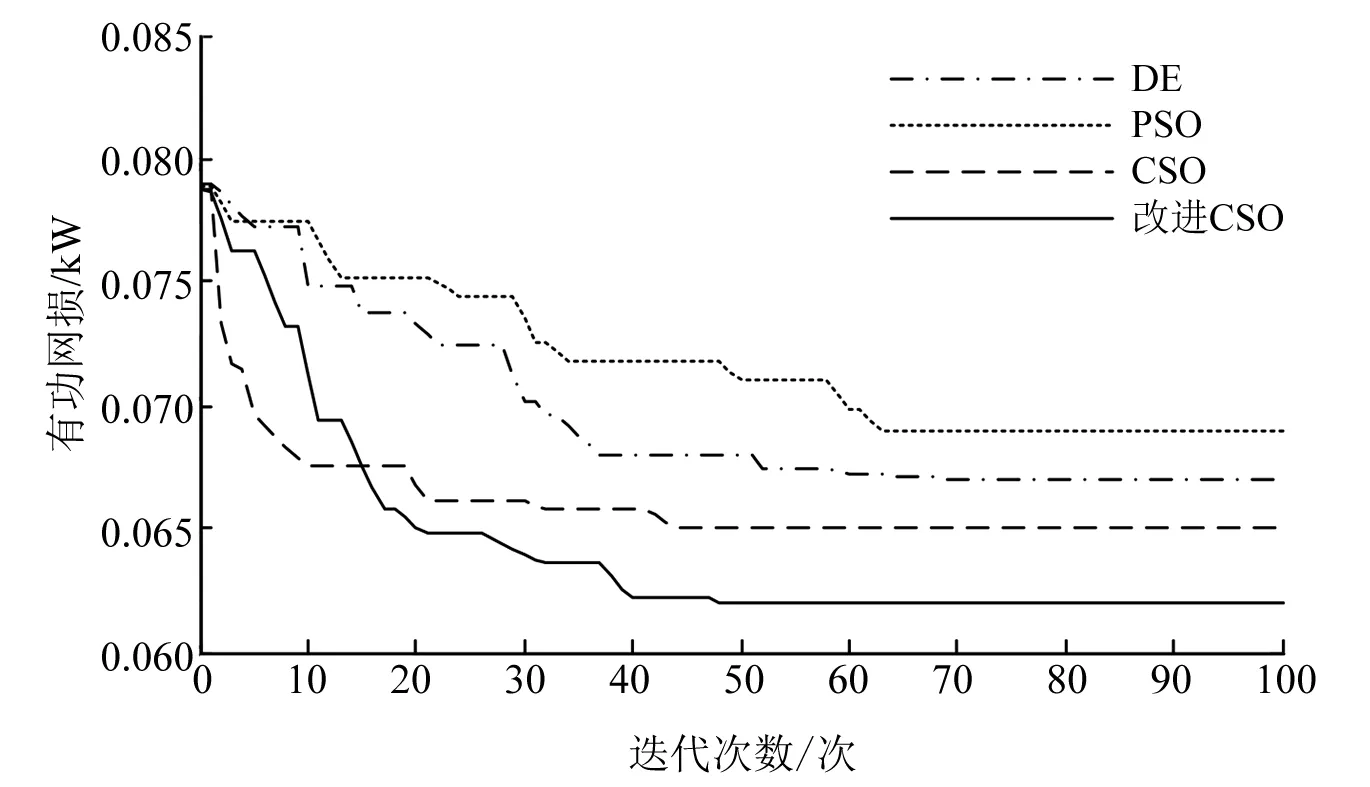
图3 4种算法的收敛曲线

5 结束语

本文提出了一种混合策略的鸡群算法，引入反向学习机制对种群进行初始化，提高算法的收敛速度。为解决母鸡容易陷入局部最优的问题，引入柯西变异来提高种群的多样性，使母鸡能跳出局部最优。对小鸡引入学习因子使其向公鸡学习，防止小鸡跟随母鸡陷入局部最优。结合无功优化的特点，从经济性出发，以有功网损最小为目标函数，使用改进的鸡群算法对其进行求解。算例结果表明，改进鸡群算法的收敛精度和收敛速度均高于其他算法。接下来的研究方向是拓展改进鸡群算法在多目标函数的应用。