基于12/8磁阻电机极性分布对电机损耗及温度场的影响

张巍， 胡泮， 朱海浪， 邵淋晶

(南京工程学院 电力工程学院，江苏 南京 211167)

0 引 言

传统能源日益枯竭，空气污染问题日益加重，新能源汽车受到越来越多的厂商关注和政府的大力扶持。而众多新能源汽车中，纯电动汽车以其更高的可靠性和能量转换效率越来越受到欢迎[1]。有效地将电池动力转换为机械能以提高行驶里程的任务在电动汽车的发展中起着重要作用。开关磁阻电机(switched reluctance motor，SRM)结构简单、坚固，转子上无永磁体和绕组，具有体积小、功耗低和轴向利用率高的优点，越来越受到各电动汽车厂商关注,其启动范围广，在启动、制动四象限运行频繁过渡的情况下具有良好的启动性能、容错能力和很高的可靠性[2]。SRM结构紧凑、绕组散热面积小和热负荷高，为了提高电动汽车SRM的工作效率，延长其使用寿命，提高电动汽车运行的可靠性，对电机损耗及温度场的研究是有必要的[3]。

SRM中铁损计算的最大困难是铁心内部磁场的复杂性和可变性[4]。开关磁阻电机磁场不是正弦波，而是高度非线性的[5]，没有简单的解析表达式。铁心的磁化也不是正弦交变的。因此传统的电机铁心求解方法无法适应于开关磁阻电机的铁心损耗[6]。

铁心不同部位的磁通密度的幅值与频率不同，很难准确计算出SRM整体的铁损。SRM铁损计算的主要任务是研究磁场，主要通过两种方法进行分析，即磁路法与有限元法。磁路法主要针对SRM铁心不同部位的平均磁通密度波形的变化，通过将非正弦波转换成几个正弦波可以计算出铁损。有限元软件的出现极大地提高了磁场分析的准确性。借助于有限元软件和计算机强大的计算能力，可以获得SRM铁心的局部磁通密度变化波形[7-8]。采用谐波分析法计算铁损，可以提高计算的准确性。

本文以三相12/8结构的SRM为例，研究了SRM铁损的计算方法，分析计算不同绕组接线方式下，不同电机极性分布对电机损耗的影响。建立基于SRM铁损的磁-热单向耦合热仿真模型，分析计算SRM的温升具体情况。

1 SRM磁场建模与分析

铁磁材料的铁损由磁滞损耗和涡流损耗组成，传统的以正弦波为基础求解的电机铁心损耗经验公式[9]如式(1)所示。

(1)

式中:PFe为电机铁损单位质量损耗；Ph和Pe分别为磁滞损耗和涡流损耗；Ch、Ce为铁心磁滞损耗系数与涡流损耗系数，与铁心的材料系数、工艺水平等有关;n=1.6～2.2，与Bm大小有关。

Ch、Ce可以通过双频法提取上述参数。以50 Hz和60 Hz下的50 W 350铁损曲线为例，可以得到Ch的值为0.028 7，Ce的值为2.7×10-4，而n的值为1.6(电机磁通密度Bm<1时，n取1.6;磁通密度Bm>1时，n取2)。此电机铁心损耗公式可以表示为：

(2)

上述公式仅仅适用于磁通密度波形为正弦波时电机铁心损耗求解。对于SRM中铁心的磁通密度不是正弦曲线，通常采用傅里叶变换方法将非正弦磁通密度波形分解为一系列正弦波形，然后计算出电机铁心各部分的铁损。

计算非正弦磁场中的铁心损耗通常将磁密曲线做傅里叶分解，再对其基波和各次谐波分别按照上式计算得到各次谐波产生的铁损值。非正弦磁场K次谐波铁损估算值公式如下：

(3)

(4)

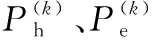
理论上，SRM铁心磁通密度波形的傅里叶变换之后，谐波的数量可以是无限的。但是随着谐波频率的增加，幅值越来越小，对电机铁心损耗的影响也越来越小[10]。因此，在计算开关磁阻电机铁心损耗时，对于高频率的谐波可以忽略不计，只需要针对有限量的谐波。如果只考虑m次谐波磁通密度波形，那么非正弦磁场铁心损耗估算公式可以表示为：

(5)

(6)

PFe=Ph+Pe

(7)

2 SRM磁场有限元分析

为了分析不同绕组接线方式下，电机不同极性分布对电机电磁特性及其损耗的影响[11]，基于电机的几何形状，使用有限元软件Maxwell建立二维有限元仿真模型。本文对比分析三相SRM样机两种不同绕组连接方式下电机的铁心损耗表现。两种绕组连接方式如图1所示。

从图1可以看出，两种连接方式都是将径向相对的定子极上的线圈以及和这两个定子极垂直方向的另外两个线圈并联组成一组绕组。不同的是图1(a)所示为对称磁场，即定子极的磁场分布为S-N-S-N-…,而图1(b)所示为不对称磁场，即定子极的磁场分布为N-N-N-S-S-S-…,这种模式下存在相邻极性相同的情况。选取这两种对称与不对称的磁场方式，更能说明在SRM不同磁极分布对电机铁心损的影响，为电机损耗绕组设计这一方面提供依据。

在MaxwellCircuit Editor中定义SRM的功率变换器模型如图2所示。线圈Lwinding、端部电阻R和端部漏感L串联起来等效为每一相的绕组，S1～S6为主开关管，D1～D6为单向二极管，D7～D10为续流二极管。

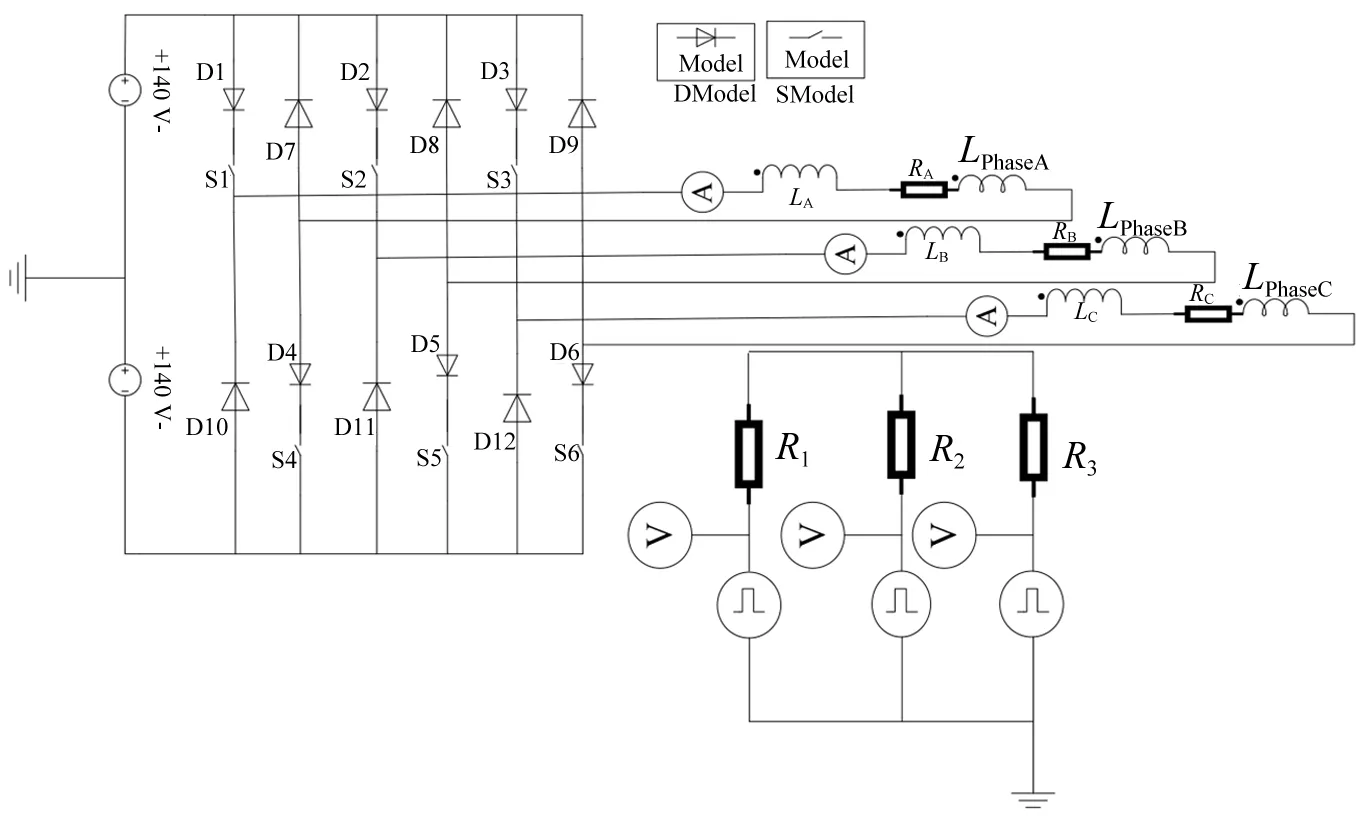
图2 功率变换器

忽略电机中的直流分量，表1为式(5)～式(7)计算不对称磁场电机的转子磁轭磁滞损耗与涡流损耗各次谐波下的铁损，并且与有限元仿真转子磁轭铁损对比。计算结果如表2所示。

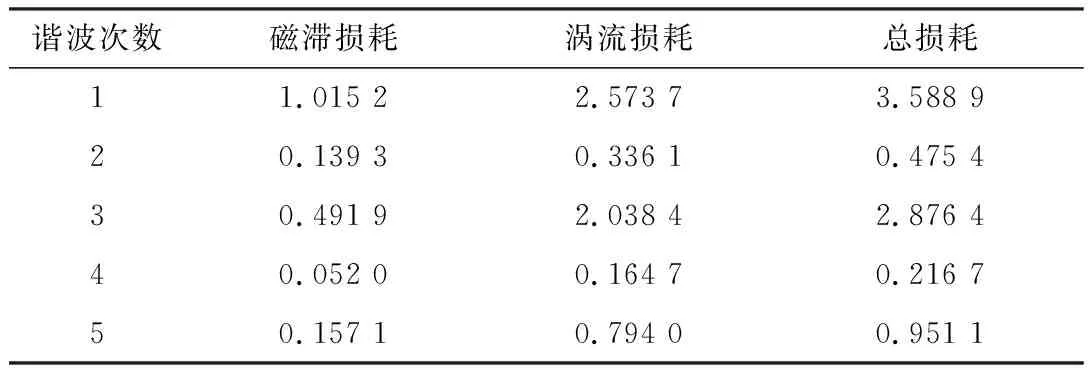
表1 不对称磁场下转子轭各次谐波铁损 W

表2 公式法与有限元法计算结果

表3中显示的基于相同驱动电路，不对称磁场N-N-N-S-S-S-…电机与对称磁场S-N-S-N-…电机各部分的铁损。

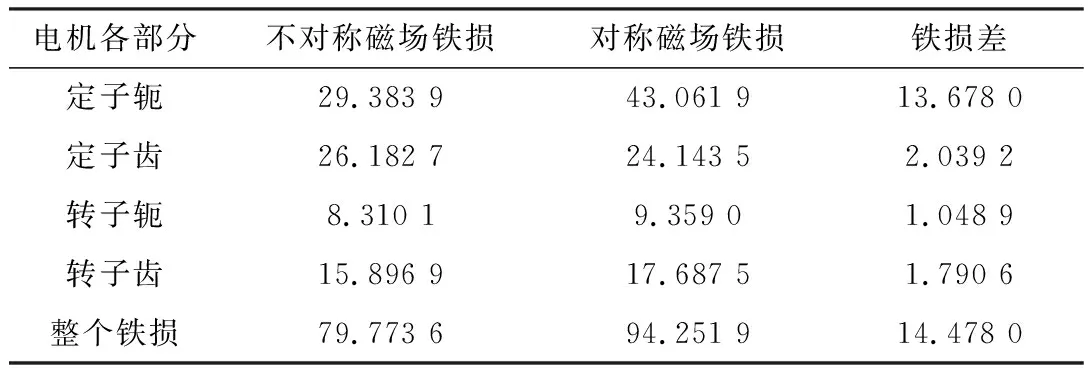
表3 不同磁极分布下铁损对比 W

根据表3中的数据可以看出电机铁心各部分的铁损。不同极性分布下定子损耗均占总损耗的大部分，分别达到69.66%、71.30%，定子轭部铁损占比分别为36.83%、45.69%，定子齿部铁损占比分别为32.83%、25.61%。转子铁损占总的铁损分别为30.34%、28.70%。对比电机在对称磁场与不对称磁场下总的铁损分别为79.773 6 W和94.251 9 W，对称磁场总的铁损比不对称磁场总的铁损多出14.478 W。这主要是因为定子磁轭铁损增加比较明显，改变了电机绕组连接方式，使电机磁极分布发生改变，造成电机定子磁轭铁损发生变化。而对称磁场下电机的平均转矩为5.008 N·m，不对称磁场下电机的平均转矩为4.734 5 N·m,仅仅增加了0.273 5 N·m。

基于有限元法计算不对称磁场下电机的不同工况的铁损。保持外加激励相同，改变电机的负载，计算出电机的铁损，如图3所示。

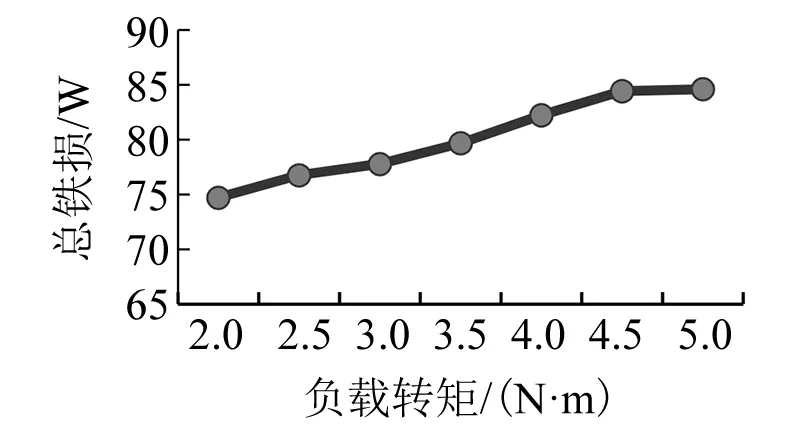
图3 不同负载下SRM的铁损

由图3可以看出，电机的损耗随着负载的增加而单调递增。而在负载增加到4.5 N·m之后，电机的损耗增长速率下降。

同样，保持外加激励相同，改变电机的转速，计算出电机的铁损如图4所示。

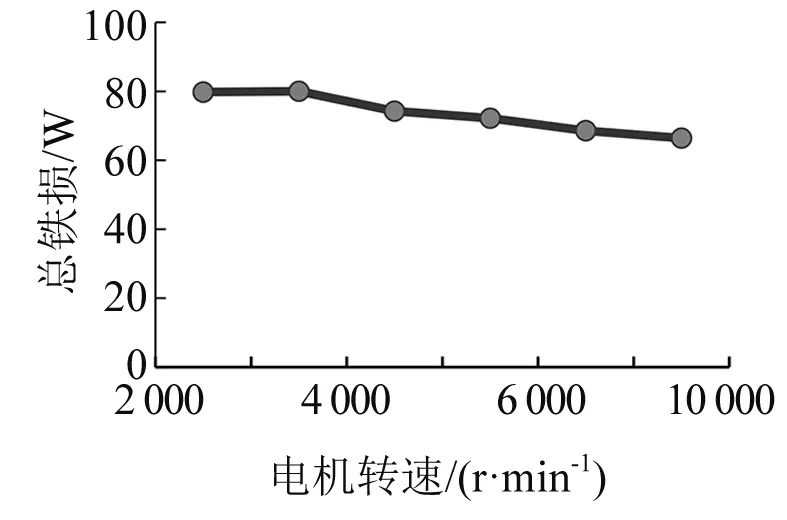
图4 不同转速下SRM的铁损

由图4可以看出，电机铁耗随着电机的转速的增加单调递减。损耗变化速率不大，可以推测在SRM空载运行下，电机的铁损变化较小。

3 温度场分析

在非对称磁场分布的SRM铁损计算模型的基础上，通过ANSYS/Transient Thermal软件建立磁-热单向耦合二维有限元热仿真模型对电机进行温度场仿真与分析。

ANSYS/Transient Thermal有限元仿真计算分析得出温度分布，如图5所示。电机的最高温度分布在SRM定子绕组部分。定子铁心的温度低于定子绕组的温度，但高于转子的温度。一方面，定子铁心的损耗即热源较大；另一方面，绕组产生的热量也可以直接传递到定子铁心上。转子铁心温度较低，原因之一是转子铁心部分的铁损较小。另外，转子和定子铁心之间存在气隙，定子铁心和绕组部分产生的热量只有很少一部分可以传递到转子铁心部分。转子结构周围存在较大空气区域，有利于电机转子铁心部分热量与气隙的交换。

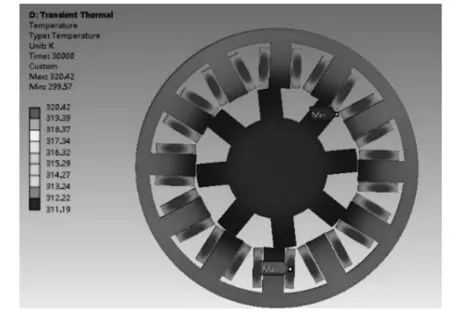
图5 SRM中温度分布

4 结束语

本文基于50W350铁磁材料的损耗曲线，建立SRM的铁心损耗计算模型。所提出的方法根据磁通密度分布计算可变损耗系数和有限数量的元素。基于在对称磁场，即定子极的磁场为S-N-S-N-…和不对称磁场，即定子极的磁场为N-N-N-S-S-S-…下的三相12/8 SRM的磁场分布，然后计算出电机的铁损。结果表明不对称磁场与对称磁场下总的铁损分别为79.773 6 W和94.251 9 W，对称磁场总的铁损比不对称磁场总的铁损多出14.478 3 W。而多出这部分损耗仅仅提升了0.273 5 N·m转矩。显然采用不对称磁场分布相比采用对称磁场分布的SRM在铁损方面更加合理科学。通过有限元仿真软件计算验证SRM铁损模型误差仅为2.426%。

通过建立磁-热单向耦合不对称磁场分布SRM模型进行温度场分析计算。电机温升最高部分集中在电机的定子绕组部分，而定子磁极相较于转子磁极部分温升较大。主要与电机铁损的大小以及电机的结构有关。

对SRM铁心损耗以及温度场分析与计算，为SRM电机的材料选择和冷却散热系统的设计等提供依据，具有实际的工程意义。