网球专项灵敏素质结构模型的构建与评价标准

彭建军，马驰宇

(武汉体育学院网球学院，湖北 武汉 430079)

随着对竞技网球的深入研究，体能训练在网球训练体系中日渐突出，广大教练员逐步意识到体能训练对网球运动员竞技水平的提高起着重要作用[1]。但是，体能包含许多项身体素质，因此在训练工作中不能胡子眉毛一把抓，而应找出与网球项目联系紧密的要素进行系统训练[2]。

网球属于技巧性很强的运动项目，需要运动员具备突然性的加速、减速、转向移动能力，以确保在比赛中能迅速、准确、协调自如地完成各项技术动作[3]。灵敏素质的定义为：人体在突然变换外界条件的情况下，改变身体运动空间位置和运动方向，从而适应不断变化的环境的一种能力[4]。由此可知，在网球比赛中，运动员一系列身体动作、移动、转向、应激行为等都需要灵敏素质的帮助。可以说，灵敏素质是身体的速度、力量等其它素质良好发挥的保证，机体灵敏素质的提高为竞技水平发展奠定了基础[5]。

K Cooke认为网球专项灵敏素质是一个多因素影响的概念，因此需要探寻一种多方面且有针对性的综合测试方法[6]。而目前，灵敏素质的测试方法主要来源于国外，我国多数教练员只是借鉴国外的一些测试方法，例如T测试[7]、六边形跳跃测试[8]、预设灵敏性测试[9]等。Ann Quinn认为简单地采用某几种方法评测运动员灵敏素质其结果往往不够全面和准确。因此本文旨在厘清网球专项灵敏素质的基本结构[10]并构建科学、合理的评价体系，为我国教练员训练、评价、选材等工作提供参考依据。

1 研究对象与研究方法

1.1 研究对象

本文以网球专项灵敏素质结构模型与评价标准为研究对象，以武汉体育学院80名网球专修学生(性别：男；年龄：17—23岁)为测试对象。

1.2 主要研究方法

1.2.1 文献资料法

在中国知网、Sciencedirect、Google学术等数据库上以“灵敏素质评价””specific-agility”“agility testing”等为关键词查阅国内外相关文献资料。选取与本研究相关的各项评价指标，为构建网球专项灵敏素质结构模型提供了理论支撑。

1.2.2 访谈法

根据研究需要，对网球和运动训练领域的专家进行访谈，了解网球运动员灵敏素质训练的相关方法与指标，为网球专项灵敏素质的结构划分提供了思路。

1.2.3 德尔斐法

根据搜集的文献资料和专家访谈得到的结果，编制《网球专项灵敏素质一级指标专家调查表》《网球专项灵敏素质二级指标专家调查表》和《网球专项灵敏素质指标权重表》进行三轮专家调查，在确定上一轮专家调查结果具有一致性后再进行下一轮调查，三轮调查时间严格遵循德尔斐法轮次间隔时间。

1.2.4 测量法

通过三轮专家调查，确定了网球专项灵敏素质结构模型的九项测试指标，测试方法如表1所示。

表1 各指标测量方法一览

1.2.5 数理统计法

本研究的数据主要运用Excel工作表和SPSS22.0进行统计、分析。采用Kappa检验、Kendall’s W检验分别对第一、二轮专家调查结果进行一致性检验，运用层次分析法(AHP)确定各级指标的权重分配，运用百分位数法制定单项指标评分标准。

2 结果与分析

2.1 网球专项灵敏素质指标体系的确立

2.1.1 一级指标的确立

2.1.1.1 一级指标的初选

灵敏素质是一个复杂的结构，笔者从灵敏素质的影响因素出发，在查阅文献和专家访谈的基础上，总结归纳了六项初选一级指标。如表2所示。

表2 初选一级指标一览

2.1.1.2 第一轮专家问卷调查结果

第一轮专家问卷调查采用“0～1”模式，即专家对初选指标只有通过和不通过之选择，变量类型属于二分类变量。用专家通过率来衡量专家对指标的认可程度，专家通过率R值计算公式如下：

R=专家赞同人数/专家总人数

公式中R的取值范围为0～1之间，R值越大表明专家对该指标的认可程度就越高。经过仔细思考及征询专家意见，本研究决定将R值小于0.6的指标予以删除。本轮次一级指标的专家通过率如表3所示。

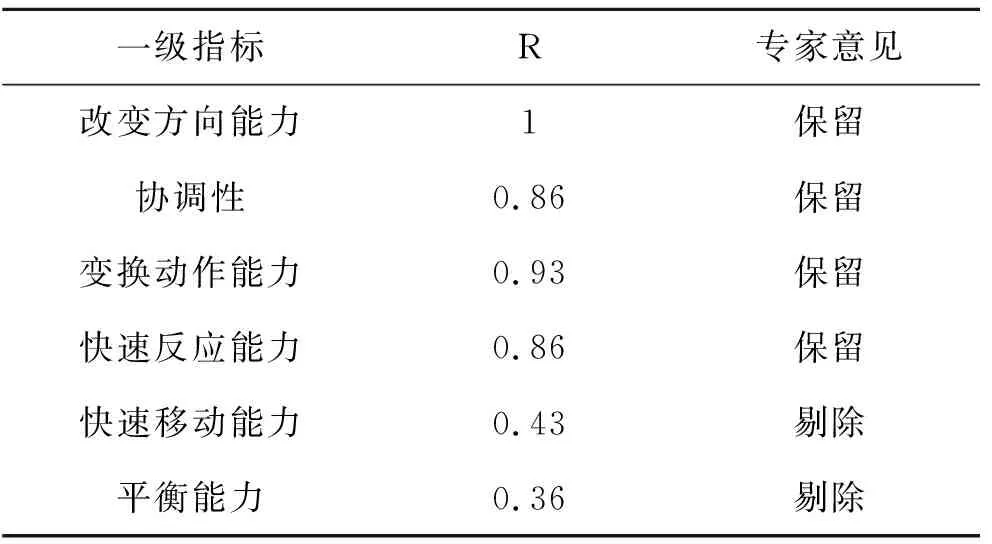
表3 第一轮专家调查结果统计表

采用Kappa系数对本轮专家调查结果进行一致性检验，结果如表4所示。根据Kappa系数关于一致性检验的评价标准，Kappa>0.8表明数据资料一致性程度高。因此可得本轮次专家调查结果整体上具有较高的一致性的结论，其调查结果可以为本研究使用。

表4 第一轮专家调查Kappa系数统计一览

通过对专家调查结果的统计和一致性检验，可以确立网球专项灵敏素质的一级指标，即网球专项灵敏素质的基本结构，主要由4个因素来决定，分别是：改变方向能力、变换动作能力、快速反应能力和协调性。很多专家学者认为改变方向能力是灵敏素质的基础，在网球运动中须迅速改变运动方向以找准击球点；良好的变换动作能力是技战术发挥的保障，运动员在比赛中需要运用各种技术动作去处理不同深度、高度、角度的球；网球比赛瞬息万变，在极短的时间里运动员良好的决策、反应能力往往是制胜的关键；协调能力是指在运动中机体对身体形态、动作、技术结构等各个环节的综合控制和优化。

2.1.2 二级指标的确立

2.1.2.1 二级指标的初选

根据第一轮调查结果，对初选二级指标进行归类，如下表5所示。

表5 初选二级指标一览

2.1.2.2 第二轮专家问卷调查结果

第二轮专家问卷调查要求所选专家采用五级评分法对所有的初选指标进行赋值，每项指标的重要程度按照“非常重要”=5分、“重要”=4分、“一般”=3分、“不太重要”=2分与“不重要”=1分分为五个等级。根据专家调查结果计算出各指标重要程度的平均分。第二轮专家调查结果如表6所示。

表6 第二轮专家调查结果一览

本研究以平均得分在3.5分以上的指标作为入选标准，同时对第二轮专家的调查结果进行了一致性检验。运用Kendall’s W检验方法，检验结果见表7，各级指标P<0.05、W>0.6，通过一致性检验，表明专家意见一致。

表7 各级指标Kendall’s W一致性检验结果

通过两轮专家问卷调查，构建出网球专项灵敏素质结构模型与评价指标体系(见表8)。从表8可知，4个一级指标重要性程度全部在4分以上，说明这4个因素能很好地解释网球专项灵敏素质的基本结构，同时可以再次证明第一轮专家问卷调查的结果具有一致性、可靠性。在改变方向能力子指标中，六边形跳跃测试、十字变向跑、蜘蛛形跑[11]的平均分都大于4分，说明这三个指标能很好地代表改变方向能力的水平。依此类推，协调性水平由1min双摇跳绳和反复横跨[12]来说明，变换动作能力由立卧撑[13]和仰卧起立来说明，快速反应能力由综合反应时[14]和六角球测试[15]来说明。

表8 网球专项灵敏素质结构模型与评价指标体系一览

2.1.3 指标体系权重的确定

权重是指根据组成事物的要素在系统中的地位和重要程度不同而赋予的一定的数值。本文构建的评价系统由多个指标构成，因此需要计算出各个指标的权重，用它来反映各个指标在评价系统中的重要程度。

本研究的指标体系是由两个层次组成，即一级指标下面包含若干二级指标，因此采用层次分析法(AHP)[16]计算各级指标的权重。网球专项灵敏素质指标层次结构模型见图1。将《网球专项灵敏素质指标体系权重表》发放给专家，根据专家问卷对同层次两两指标的相对性重要程度的平均打分情况，计算出各层判断矩阵并输入到SPSSAU软件里进行系统分析。

图1 网球专项灵敏素质结构图

(1)一级指标权重

一级分析结果如下表9所示。根据表中权重值数据对一级指标权重进行归一化处理，得出一级指标的最终权重分配为：A1∶A2∶A3∶A4=0.45∶0.26∶0.13∶0.16。表中CR值[17]为0.012<0.1，意味着本次研究判断矩阵满足一致性检验，计算所得权重具有一致性。

表9 一级指标层次分析结果

(1)二级指标权重

二级指标分析结果见表10～表13。由表10可知：各层次相对应的CR值均小于0.01，满足判断矩阵的一致性要求。并对同层次二级指标的权重进行归一化处理，可以得出B1∶B2∶B3=0.32∶0.22∶0.46、B4∶B5=0.60∶0.40、B6∶B7=0.57∶0.43、B8∶B9=0.42∶0.58。

表10 A1-B层析分析结果

表11 A2-B层析分析结果

表12 A3-B层析分析结果

表13 A4-B层析分析结果

运用层次分析法，可以确定网球专项灵敏素质结构模型的权重体系，见表14。根据各级指标的权重分配，建立网球专项灵敏素质评价函数：

表14 指标体系权重系数一览

F=0.45*(0.32B1+0.22B2+0.46B3)+0.26*(0.60B4+0.40B5)+0.13*(0.57B6+0.43B7)+0.16*(0.42B8+0.58B9)

2.2 网球专项灵敏素质评价标准的建立

2.2.1 各指标样本的采集与统计

网球专项灵敏素质结构模型构建完成后，需要对各项子能力的若干指标进行样本数据采集，样本容量为80，由本人监督测试过程，各运动员测试三次，取最好成绩。样本数据统计结果见表15。

表15 样本测试数据统计一览

2.2.2 单项指标评价标准的建立

本研究运用百分位数法[18]，以5分为间距，分别计算出0、5、10、15、20……100分对应的指标数值区间，建立单项评分标准(见表16)，须注意的是本研究除了B4(1min双摇跳绳)是高优指标，其它各二级指标均为低优指标。

表16 单项指标评分标准

灵敏素质是一个多因素的概念，在评价时要考虑所有可能影响表现的因素，通过单项指标评分标准，可以确定运动员个人资料中需要注意的领域，便于运动员改善具体的薄弱环节，以提高他们在球场上的灵敏性。

2.2.3 综合评价等级的建立

根据80名运动员灵敏素质的加权总分，按照“优”占10 %(90 %及以上)、“良”占15 %(90 %～75 %)、“中”占50 %(75 %～25 %)、“下”占15 %(25 %～10 %)、“差”占10 %(10 %及以下)这五个等级进行综合评价。其结果如表17所示。

表17 综合评价标准表

根据运动员网球专项灵敏素质综合评价标准，我们可以明确地对运动员灵敏素质发展水平进行客观的评价，发现运动员个体处于整体水平的什么位置，便于教练员对运动员竞技状态有更好的掌控。

2.2.4 综合评价标准的回代检验

判断建立的评价标准是否具有可靠性和稳定性，需要对评价标准进行回代检验。为了有效降低回代检验的偶然性与片面性，进行两次抽样检验。第一次按照运动等级抽取10人，第二次依据专项训练年限抽取10人，两次抽样回代检验结果见表18和表19。

表18 第一次回代检验结果一览

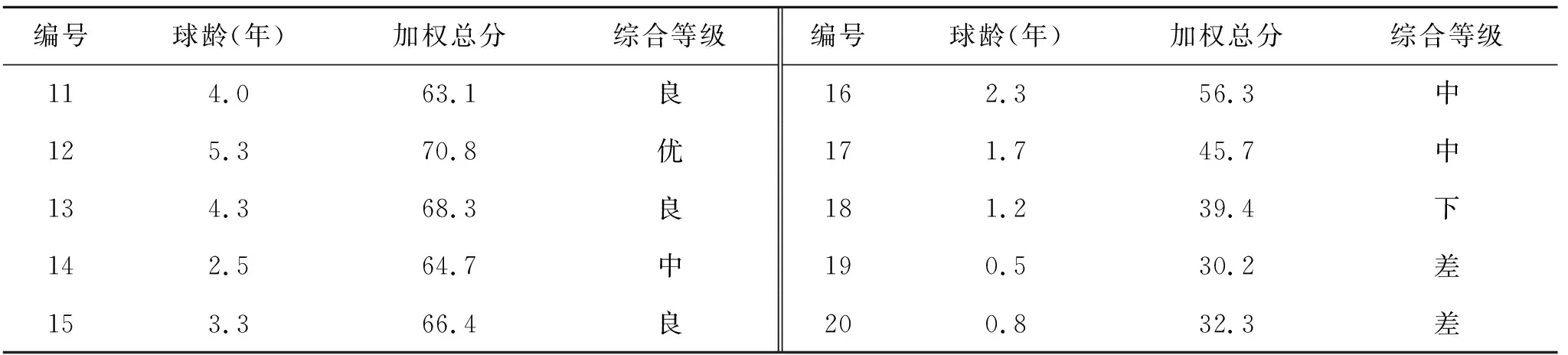
表19 第二次回代检验结果一览

从两次回代检验可以看出，专项训练年限长、水平等级较高者，灵敏素质综合得分较高，而训练时间短、运动水平较低者，综合得分较低。两次回代检验结果可以证明综合评价标准具有可靠性，同时也符合网球专项灵敏素质个体差异性的特点。

3 结论与建议

3.1 结论

(1)本研究构建的网球专项灵敏素质结构模型由改变方向能力、协调性、变换动作能力与快速反应能力等4个一级指标和六边形跳、十字变向跑、蜘蛛形跑、1 min双摇跳绳、反复横跨、立卧撑、俯卧起立、综合反应时与六角球测试等9个二级指标分层构成。

(2)根据各级指标的权重分配，建立网球专项灵敏素质评价函数：F=0.45*(0.32B1+0.22B2+0.46B3)+0.26*(0.60B4+0.40B5)+0.13*(0.57B6+0.43B7)+0.16*(0.42B8+0.58B9)。

(3)制订了包含单项指标评分标准和综合评价标准的网球专项灵敏素质评价标准，经回代检验证明：合理、可靠、有效、可操作性强。

3.2 建议

(1)灵敏素质的发展是一个动态的过程，在不同水平、不同年龄阶段要建立相应的评价标准，这样才能准确、科学地作出评价。

(2)此评价标准是以17～23岁网球运动员为测试对象，可以作为网球单招或专项考试标准以及高校高水平网球运动员选材的参考依据。

(3)本研究筛选出的二级指标不仅可以作为测试指标，也可作为教练员辅助训练手段。