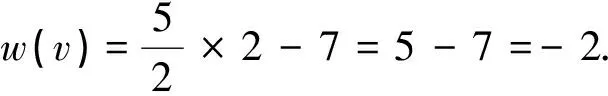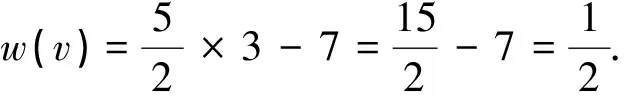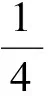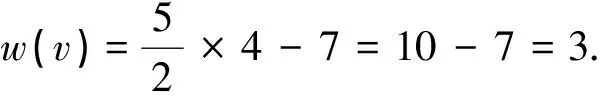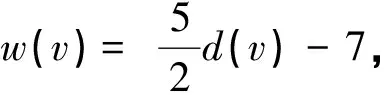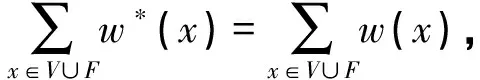平面图的2-面染色的一点注记
王剑宇
(南京晓庄学院 信息工程学院,江苏 南京 210017)
本文所研究的图均为简单无向图.如果没有特殊说明,所有的定义和术语均可参考[1].以下先给出本文要用的一些定义.
设图G=(V,E),其中顶点集是V,边集是E.对于G的顶点v,如果d(v)=k,则点v称为k-点;如果d(v)≥k,则点v称为k+-点;如果d(v)≤k,则点v称为k--点.如果顶点v满足d(v)=k,且关联i个2-点,则称v是ki-点.图G中,最短圈的长度称为G的围长,记为g(G)或g.
若φ是一个从顶点集V到颜色集{1, 2, …,k}的一个映射φ:V→{1, 2, …,k},使得对于任意u,v∈V,uv∈E,满足φ(u)≠φ(v),则称φ是图G的一个正常k-染色.使得G存在正常k-染色的最小整数k,称为G的染色数,记为χ(G).
一个图G称为是平面图,是指存在的G的一个平面嵌入,使得每条边只在顶点相交.平面图G的顶点集、边集、面集分别记为V,E,F.给定平面图G和正整数l,G的一个l-面染色是指对图的G顶点染色,使得对于任意两个顶点,如果它们在同一个面上,且之间存在不超过l的通路,所染的颜色不同.G的l-面染色所用的最少的颜色数称为G的面染色数.显然,平面图的1-面染色就是点染色,因此,l-面染色是点染色的自然推广.
总体而言,平面图的l-面染色猜想是公开的,甚至当l=2时也没有解决.
本文主要证明了如下定理:
定理1:如果G是平面图且围长至少是7,那么G的2-面染色数至多是7.
定理1改进Micka⊇l Montassier和André Raspaud[3]的部分结论,并且表明如果平面图G的围长至少是7时,平面图l-面染色猜想对于l=2是成立的,对于该猜想的成立提供了正面的支持.
定理1的证明方法主要采用色扩张和权转移方法,在下文中,第一部分主要讨论关于定理1的极小反例的结构性质,第二部分利用权转移方法证明定理1的极小反例不存在,从而定理1成立.
1 最小反例的结构引理
本节主要讨论极小反例的结构.假设G是一个定理1的最小的反例,即指,G是一个g≥7的平面图,但G不能用7种颜色进行2-面染色,而G的任意一个真子图G′存在2-面染色只用最多7种颜色.显然,不妨假设G是连通的.
以下,我们证明若干引理:
引理1:G中不含1-点.
证明:假设v是G中的一个1-点,u是唯一一个和v相邻的点.设u1、u2与u相邻(见图1(a)).因为G是最小的反例,所以G-{v}可用最多7种颜色进行2-面染色.只要让v的颜色与u1、u2、u的颜色不同,则G也可用最多7种颜色进行2-面染色.
引理2:G中不含相邻的2-点.
证明:假设v和w是G中的两个相邻的顶点,且d(v)=d(w)=2.设u1、u2与u相邻,x1、x2与x相邻(见图1(b)).因为G是最小的反例,所以G-{v,w}可用最多7种颜色进行2-面染色.只要让v的颜色与u1、u2、u、x的颜色不同,w的颜色与u、v、x、x1、x2的颜色不同,则G也可以用最多7种颜色进行2-面染色.
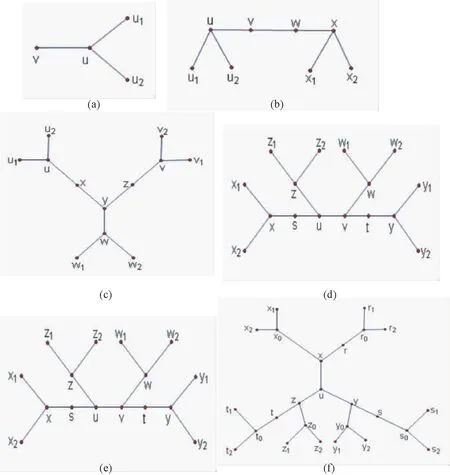
图1 最小反例中的局部结构
引理3:G中的3-点最多与一个2-点相邻.
证明:假设G中的一个顶点y与x、z、w相邻,其中d(y)=3,d(x)=d(z)=2,d(w)≥2.设u与x相邻,v与z相邻,u1、u2与u相邻,v1、v2与v相邻,w1、w2与w相邻(见图1(c)).因为G是最小的反例,所以G-{x,y,z}可用最多7种颜色进行2-面染色.只要让x的颜色与u1、u2、u、w的颜色不同,y的颜色与u、x、w、w1、w2、v的颜色不同,z的颜色与w、x、y、v、v1、v2的颜色不同,则G也可用最多7种颜色进行2-面染色.
引理4:G中不含相邻的31-点.
证明:假设G中有两个31-点u和v相邻.设s、z与u相邻,w、t与v相邻,x1、x2与x相邻,y1、y2与y相邻,z1、z2与z相邻,w1、w2与w相邻(见图1(d)).因为G是最小反例,所以G-{u,v,s,t}可用最多7种颜色进行2-面染色.只要让u的颜色与x、z、z1、z2、w的颜色不同,v的颜色与z、u、w、w1、w2、y的颜色不同,s的颜色与x1、x2、x、u、z、v的颜色不同,t的颜色与u、v、w、y、y1、y2的颜色不同,则G也可用最多7种颜色进行2-面染色.
引理5:G中的4-点最多与两个2-点相邻.
证明:假设G中的一个4-点u与x、y、z、w相邻,其中d(x)=d(y)=d(z)=2,d(w)≥2.设s与x相邻,t与y相邻,v与z相邻,s1、s2与s相邻,v1、v2与v相邻,t1、t2与t相邻,w1、w2与w相邻(见图1(e)).因为G是最小的反例,所以G-{u,x,y,z}可用最多7种颜色进行2-面染色.只要让u的颜色与s、v、t、w、w1、w2的颜色不同,x的颜色与s1、s2、s、u、w的颜色不同,y的颜色与x、u、w、t、t1、t2的颜色不同,z的颜色与x、u、w、y、v、v1、v2的颜色不同,则G也可用最多7种颜色进行2-面染色.
引理6:G中的3-点最多与两个31-点相邻
证明:假设G中的一个3-点u与x、y、z相邻,其中x、y、z均为31-点.设x0、r与x相邻,y0、s与y相邻,z0、t与z相邻,且d(r)=d(s)=d(t)=2,x1、x2与x0相邻,y1、y2与y0相邻,z1、z2与z0相邻,r0与r相邻,s0与s相邻,t0与t相邻,r1、r2与r0相邻,s1、s2与s0相邻,t1、t2与t0相邻.因为G是最小的反例,所以G-{u,x,y,z,r,s,t}可用最多7种颜色进行2-面染色(见图1(f)).只要让x的颜色与x1、x2、x0、r0的颜色不同,y的颜色与y1、y2、y0、s0、x的颜色不同,z的颜色与z1、z2、z0、t0、x、y的颜色不同,u的颜色与x、x0、y、y0、z、z0的颜色不同,r的颜色与r1、r2、r0、x、x0、u的颜色不同,s的颜色与s1、s2、s0、y、y0、u的颜色不同,t的颜色与t1、t2、t0、z、z0、u的颜色不同,则G也可用最多7种颜色进行2-面染色.
2 权转移及定理的证明
本节利用权转移方法并结合最小反例的结构引理证明最小反例不存在.
引理7:每个连通的平面图(V,E,F)满足:
(1)

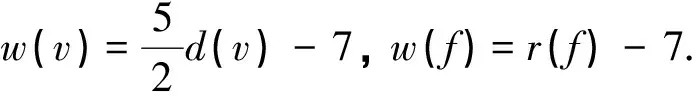

(2)
我们给定以下权转移规则:
规则1:每个3+-点转移权值1给相邻的2-点.
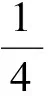
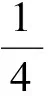
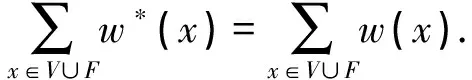
下面验证G的顶点和面的新权重.
∀f∈F,因为g≥7,w*(f)=w(f)≥0.
∀v∈V,设v是G中的一个k-点(k≥2),则: