不同轴压比与剪跨比的RC异形柱抗爆分析

周清齐麟

(1.滨州市规划设计研究院，山东 滨州256600；2.中国民航大学 机场学院，天津300300)

0 引言

钢筋混凝土RC(Reinforced Concrete)异形柱已广泛地应用于结构设计中，异形柱宽度可以设计成与墙体相同，从而避免了类似框架结构因框架柱凸出墙面过多影响使用要求的缺点。抗震设计中，轴压比和剪跨比是重要的控制参数[1]，轴压比过大或者剪跨比过小均会对构件造成破坏，因此选择合适的轴压比与剪跨比是改善结构抗震性能的重要途径。由于爆炸荷载的特殊性及危险性，抗爆试验较普通结构试验要求更加严格，所以结构抗爆分析多采用数值分析的研究方法[2]。许多学者采用数值分析方法对爆炸荷载下RC异形柱的动力响应与破坏进行了深入的研究。王傲等[3]研究了钢管直径对T形截面钢管混凝土芯柱抗爆性能的影响，结果表明T形钢管混凝土芯柱的抗爆性能随着钢管直径的增大而增强。任琳琳[4]就L形钢骨异形柱的抗爆性能的有限元分析指出，采用合理的端部约束可以提高L形钢骨混凝土异形柱的抗爆性能。张磊[5]对爆炸荷载作用下混凝土异形柱框架结构的倒塌性能的研究表明，失效柱所在楼层越低，结构的抗倒塌能力越强。敕勒格尔[6]研究了爆炸荷载作用下十字形截面钢骨混凝土异形柱的受力性能，发现长细比与十字形截面钢骨混凝土柱在爆炸荷载作用下的柱中位移成正比。为研究轴压比和剪跨比对RC异形柱抗爆性能的影响，文章在上述研究的基础上，并结合相关试验文献，验证了数值分析方法的正确性，选择合理的钢筋与混凝土材料模型，借助仿真分析软件LS-DYNA分析了爆炸荷载作用下不同轴压比与剪跨比RC异形柱的动力响应与柱底内力。

1 RC柱数值分析材料模型的选择

虽然目前国内外文献中尚未发现有关RC异形柱的抗爆试验研究，但可以借鉴对RC普通柱抗爆试验的研究结果来验证数值分析方法的正确性，以选择合理的材料模型。宗周红等[7]对RC柱进行了抗爆试验，试验柱高3.5 m，柱约束形式为柱底固定与柱顶铰接；柱截面为圆形，直径为400 mm；柱纵筋为1012，纵筋按照环形均匀布置，箍筋为8＠150。试验设计了多种工况，选择具有代表性的工况5进行分析，工况5采用接触爆炸的形式，三硝基甲苯TNT药量为2 kg。采用LS-DYNA中的J-C模型(*MAT＿015)模拟 钢筋、KCC模 型(*MAT＿072R3)模拟混凝土，建立与工况5完全相同的有限元模型如图1所示。

图1 文献[7]中的试验布置与其对应的数值分析模型图

根据文献[7]可知，在接触爆炸后，试件在0～60 cm范围内被完全炸断，纵筋出现非常大的(拉或压)变形，箍筋已经完全脱离柱体，混凝土酥松剥落，没有较大的混凝土飞溅块，有大量宽的斜裂缝从断裂处向柱身发展。工况5试验前后与数值分析结果的对比如图2所示，数值分析结果在破坏形态、破坏高度和钢筋变形的各方面均与试验结果吻合较好。

建筑材料在爆炸冲击作用下，可能经历高达每秒10～1000的应变率。在这种高应变率情况下，其强度、弹性模量等都会有一定程度的提高，这种特性称为应变率效应。文献[2]在应变率效应的情况下，钢筋强度、混凝土的抗压强度、抗拉强度分别提高了50%、100%、600%。综上所述，抗爆分析中选择混凝土材料模型必须要考虑其应变率效应。

图2 试验前后与数值分析结果的对比图

钢筋采用LS-DYNA中的J-C模型，模型需要定义的钢筋材料参数如下:密度ρ1为7 850 kg/m3、弹性模量E为2.06×105MPa；泊松比ν为0.3、切线模型Etan为2.06×103MPa；与应变率效应有关的参数A、B、n、C分别为404、232.4 MPa和0.31、0.018；钢筋的失效应变取值为0.16。

混凝土采用LS-DYNA中的KCC模型，模型需要定义的混凝土材料参数如下:密度ρ2为2 320 kg/m3、初始强度fc为40 MPa；单位转化值RSIZE、UCF分别为39.37、145×10-6。KCC模型直接调用723＃曲线实现混凝土材料的应变率效应。

2 RC柱计算模型的改进与数值分析材料模型建立

2.1 改进后的RC柱计算模型

在进行结构抗爆分析时通常将RC柱约束形式设计为两端固定[8-10]，而现实中的柱顶并非单纯的固定端约束。真实的框架柱柱顶四周与框架梁相交形成梁柱节点核心区，并且在较大的爆炸荷载作用下会产生一定的水平位移。某地意外爆炸后的框架结构破坏如图3所示，爆炸荷载作用下，框架结构中柱发生严重的破坏，中柱沿爆炸作用方向产生较大的水平位移；梁柱节点发生严重破坏，梁柱相交处产生较大的裂缝。为使计算模型与实际破坏形态相一致，采用以下方法对其进行改进:(1)由于柱底与基础相连，柱底采用固定端约束。(2)柱顶由梁柱节点、与节点相连接的框架梁组成。爆炸荷载作用下柱会沿着作用方向产生一定的水平位移，故对该方向的框架梁采用水平支座约束；与柱相交的框架梁仅在节点周围产生变形，而远离节点的框架梁基本保持原状。故仅建立部分框架梁模型，梁段长度取值500 mm，梁端采用固定端约束。(3)在柱顶施加竖向荷载以研究不同轴压比柱的抗爆性能。

常用框架柱与改进后框架柱的计算模型如图4所示，通过与图3对比可知，改进后的框架柱计算模型能更准确地反映其在爆炸荷载作用下的破坏形态。

图3 爆炸后框架图

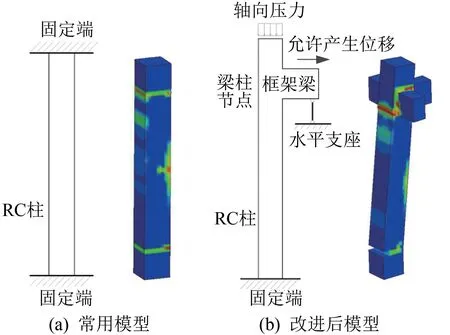
图4 常用框架柱计算模型及改进后的计算模型图

2.2 数值分析的材料模型

利用LS-DYNA软件对RC柱进行数值分析时需要选择钢材、混凝土、空气和炸药4种不同的材料模型。其中HRB400钢筋、C40混凝土材料分别采用J-C模型、KCC模型。添加关键字*MAT＿ADD＿EROSION定义混凝土材料的破坏，采用最大主应变值0.15作为失效准则。

炸药采用*MAT＿HIGH＿EXPLOSIVE＿BURN模型配合JWL方程[11-12]定义。以炸药爆轰产物的压力由式(1)表示为

式中P1为爆炸压力，MPa；V为相对体积；E0为初始内能密度，J/m3；A、B、R1、R2、ω为状态方程参数。其具体数据为:密度ρ为1 631 kg/m3、参数A、B分别为371.2、3.23 GPa，参数R1、R2、ω分别为4.15、0.95、0.30，初始内能密度E0为7×109J/m3。

空气采用*EOS＿LINEAR＿POLYNOMIAL状态方程[14]定义，空气压力与相对体积的关系由式(2)表示为

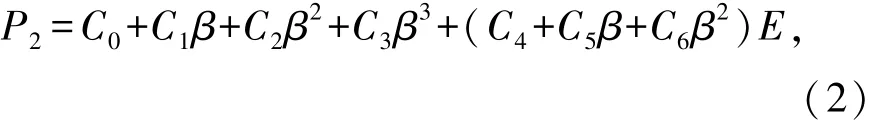
式中β为空气的相对体积，β＝(1/V)-1；P2为空气压力，MPa；C(i＝0，1，2，…，6)为多项式方程系数；E为内能密度，J/m3。各相关参数密度ρ为1.293 kg/m3，C0为-0.1 MPa，而C1、C2、C3、C4、C5均为0.4，C6为0，内能密度E为2.53×105J/m3，V为1。

炸药与空气定义为欧拉几何实体，混凝土定义为拉格朗日几何实体，采用流固耦合的方式(ALE方法)定义爆炸波与结构体、钢筋与混凝土单元的接触[15]。利用关键字*DEFINE＿CURVE配合关键字*LOAD＿BODY＿Y定义RC异形柱竖直方向的重力，重力加速度取值9.81 m/s2。利用关键字*RIGIDWALL＿PLANAR定义刚性地面以考虑爆炸波的反射作用。

3 不同轴压比与剪跨比的RC异形柱抗爆分析

按照相关规范要求建立3种截面的RC异形柱[15]:L形、T形、十字形。柱高为3.5 m、柱截面厚度为200 mm、柱肢长度为500 mm，3种截面面积均为0.16 m2。纵筋为1216、配筋率为1.51%、箍筋配筋为10＠100、体积配箍率为1.67%。采用改进后的柱顶约束条件，异形柱柱顶分别与框架梁相连接形成梁柱节点核心区，如图5所示。爆炸力学采用爆炸点至结构的距离R与药量W13的比值(定义为比例距离Z)作为衡量爆炸超压作用的单位。相同R的条件下，W越大则Z越小，产生的超压荷载越大。为研究爆炸荷载作用下结构构件的动力响应及破坏特征，需对爆炸荷载进行限制，所采用的爆炸荷载应既能使结构构件发生一定程度的破坏又不至于使其完全破坏。为满足上述要求经过多次试算，爆炸点位置选择距离柱底R为3 m处，W取值为20 kg，此时所对应的Z为按上述条件建立的有限元模型如图6所示。

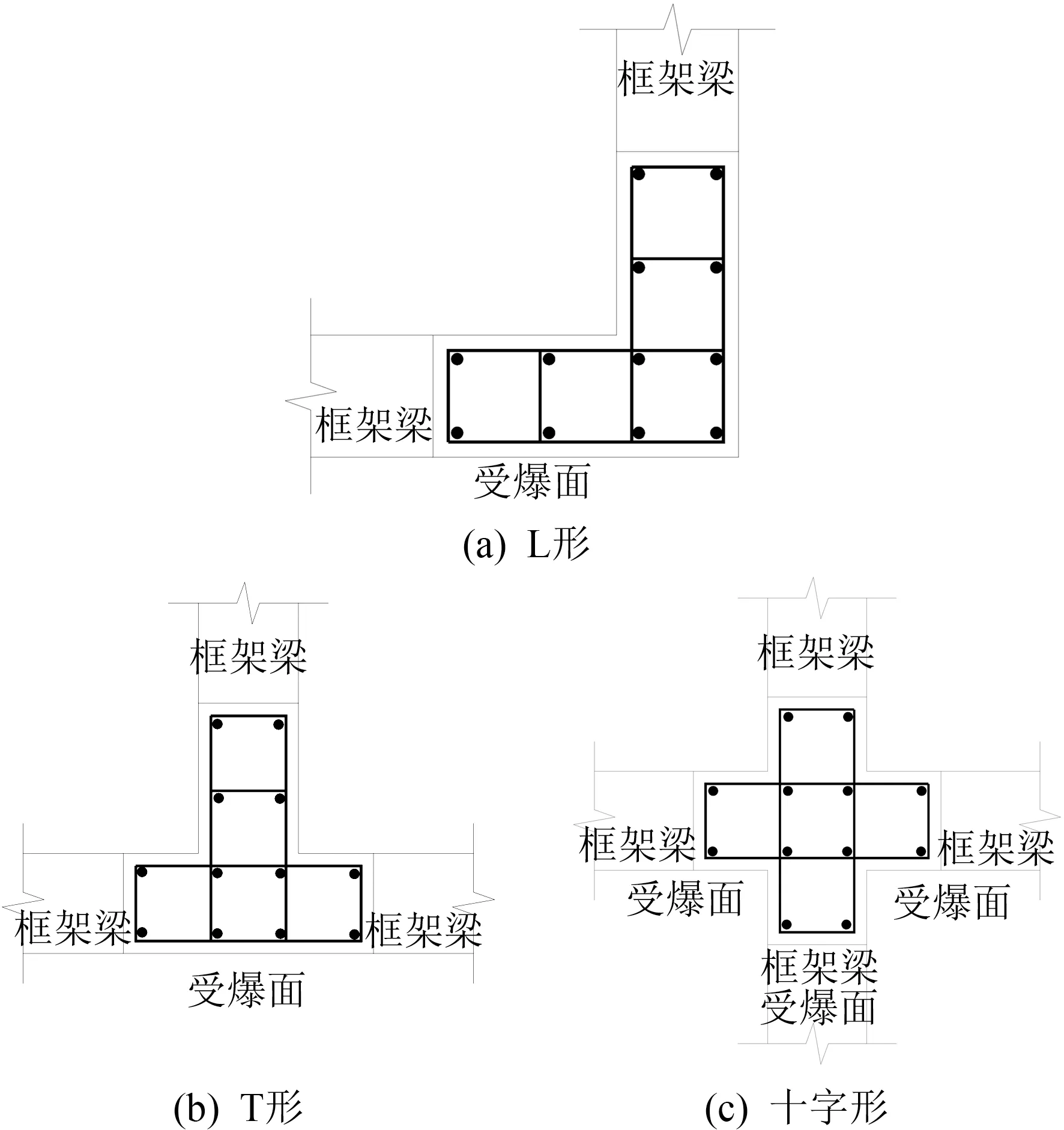
图5 RC异形柱的3种不同截面形式图

图6 有限元模型图

3.1 爆炸荷载下不同轴压比RC异形柱的动力响应及柱底内力分析

将轴压比公式μ＝N/(fc×A)变为P3＝N/A＝fc×μ，其中fc为C40混凝土的轴心抗压强度，其大小为19.1 MPa。将轴压比以面荷载P3的形式施加于柱顶，由于3种截面面积相等且均为0.16 m2，则轴压比μ为0.1、0.2、0.3时所对应的面荷载P3分别为1.91、3.82和5.73 MPa。

Z为的爆炸荷载下的不同轴压比RC异形柱的破坏形态如图7所示。当μ＝0时，3种截面RC异形柱破坏程度均较小，破坏的主要范围为柱底与梁柱节点，表现为柱底正面(迎爆面)混凝土单元发生受拉破坏，而L形柱除柱顶与梁柱节点处发生破坏以外，柱中部背面墙肢混凝土也出现裂缝。μ＝0.1时，L形、T形柱破坏程度较μ＝0时有所增加，而十字形柱破坏程度仍然较小，柱底混凝土裂缝消失而柱中破坏程度增加，L形柱背面柱中部位混凝土出现较大裂缝，T形柱柱中截面发生弯折并沿爆炸反方向产生位移；μ＝0.2时，L形、T形柱均发生较大破坏而十字形柱破坏程度较小。L形柱跨中两墙肢相交处产生很大的破坏，两墙肢基本断开，而T形柱在柱中位置折为两端且钢筋被拉断。μ＝0.3时，3种异形柱均发生严重破坏。L形柱柱顶完全破坏并且两墙肢完全分离，T形柱折为数段，而十字形相对破坏程度较小，主要表现为柱顶混凝土被压碎。

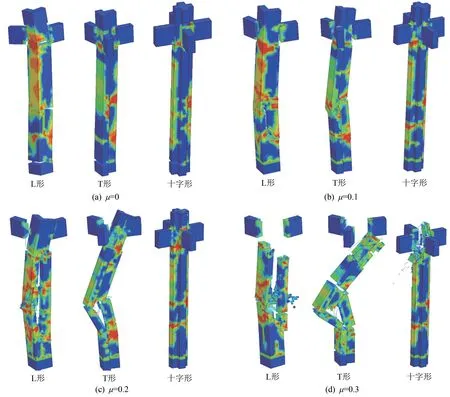
图7 爆炸荷载下不同轴压比的RC异形柱破坏形态图

3.1.1 爆炸荷载下不同轴压比的RC异形柱柱中位移动态响应分析

Z为的爆炸荷载下不同轴压比的RC异形柱柱中位移时程曲线如图8所示。当μ＝0时，各柱仅在爆炸波作用方向产生位移，按照由大到小的顺序为L形柱(140 mm)＞T形柱(111 mm)＞十字形柱(57 mm)。当μ＝0.1时，在较小的轴力作用下T形柱向爆炸波作用的反方向弯折产生较大的位移，而L形柱与十字形柱沿爆炸波方向的位移明显减小；当μ＝0.2时，随着轴压比的增加，T形柱沿爆炸波反向的柱中位移进一步增大，L形柱也产生了沿爆炸波反向的柱中位移，十字形柱位移很小基本稳定在初始位置；当μ＝0.4时，L形柱与T形柱均发生严重破坏，T形柱柱中截面位移约为L形柱的6倍，而十字形柱柱中位移仍然很小。从柱中位移分析，各柱抗爆能力由大到小的顺序依次为十字形柱＞L形柱＞T形柱。

3.1.2 爆炸荷载下不同轴压比的RC异形柱柱底内力分析

在爆炸荷载与轴向压力的共同作用下，异形柱底部会产生偏心受压破坏，借助关键字*DATABASE＿SECFORC可以得到柱底截面的内力曲线。爆炸荷载作用下μ＝0的各截面异形柱柱底轴力与弯矩曲线如图9所示。μ＝0时各柱柱底轴力均较小而弯矩较大，最大弯矩与最大轴力同时出现。定义弯矩与轴力的比值为偏心距，即e＝M/N。e较大时表现为大偏心受压破坏特征，较小时表现为小偏心受压破坏特征。此时，L形、T形、十字形的偏心距分别为0.59、0.75、0.57 m。结合图7中μ＝0时的柱底破坏图可知，此时柱底混凝土表现为大偏心受压破坏特征，迎爆面方向的混凝土因受拉产生较大的裂缝。

爆炸荷载下不同轴压比的各异形柱柱底内力值汇总见表3。表中“-”表示轴向压力与沿爆炸波作用方向的弯矩。随着轴压比的增加柱底轴向压力与弯矩均逐渐增大。同时，柱底截面处的偏心距逐渐减小，柱由大偏心受压状态转变为小偏心受压状态。结合图7中柱的破坏形态可以直观地看出，随着轴压比的增加，柱底破坏逐渐降低，混凝土受压区域逐渐增加，表现出小偏心受压的特征。

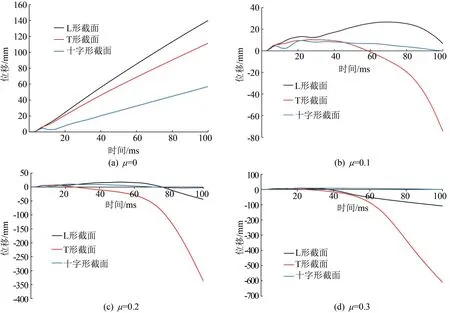
图8 爆炸荷载下不同轴压比的RC异形柱柱中位移时程曲线图

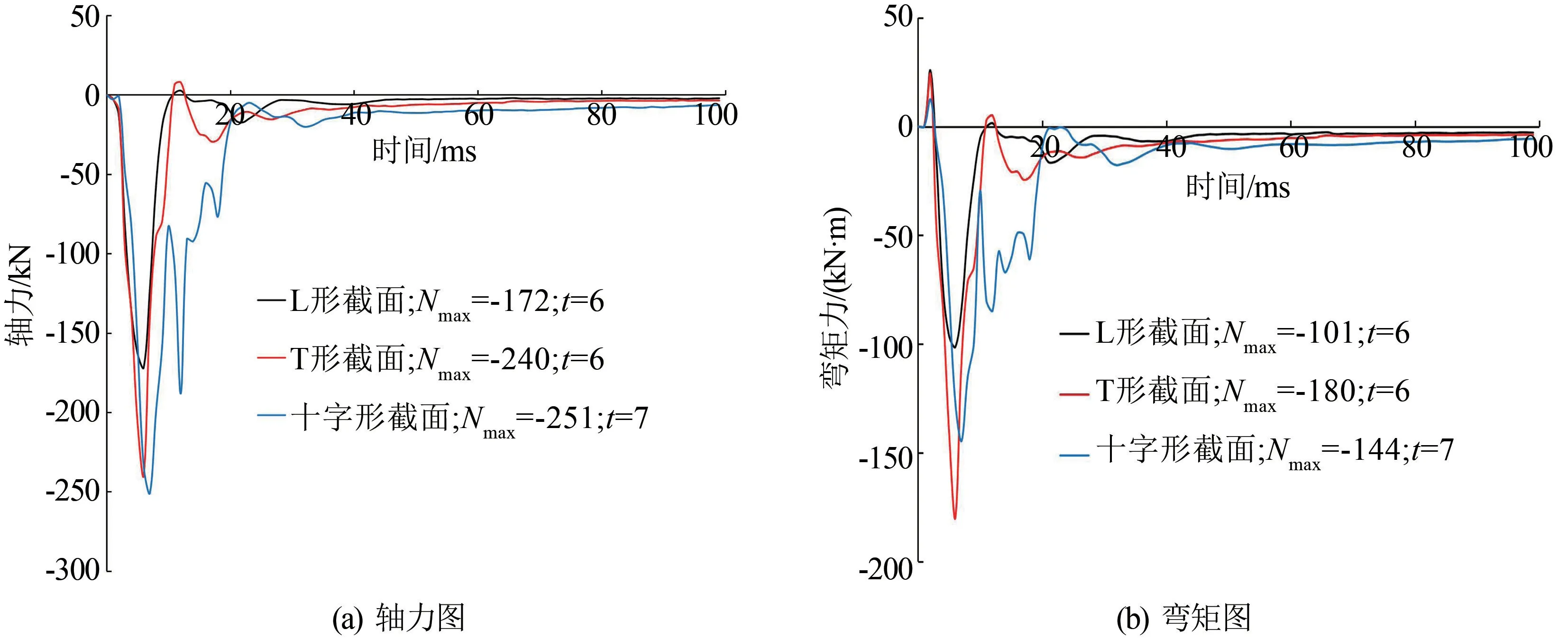
图9 爆炸荷载下μ＝0时的RC异形柱柱底内力曲线图

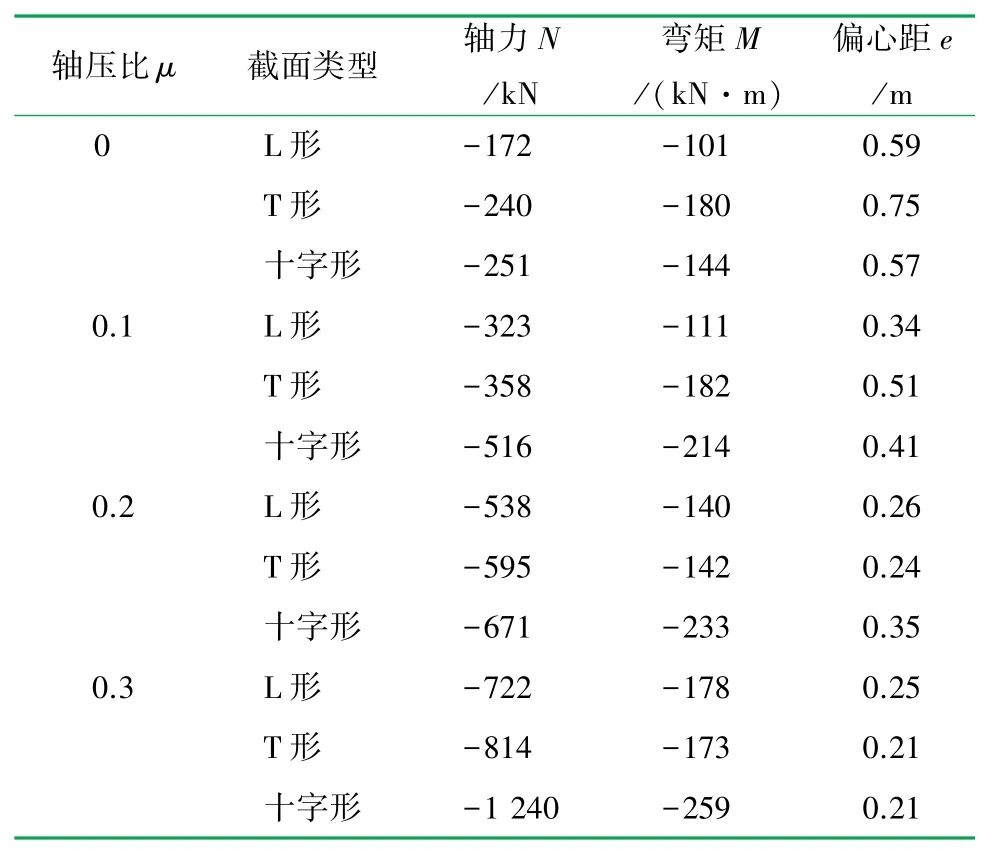
表3 爆炸荷载下不同轴压比各柱柱底内力汇总表

3.2 爆炸荷载下不同剪跨比RC异形柱的动力响应及柱底内力分析

框架结构中，柱净高与2倍柱截面有效高度的比值定义为剪跨比，即λ为Hn/(2×h0)。柱高3.5 m时，剪跨比λ为3.68。为研究爆炸荷载作用下不同剪跨比异形柱的抗爆性能，将柱净高Hn依次改变为3.0、2.5、2.0 m，对应的λ分别为3.16、2.63和2.11。上述不同λ的异形柱在Z为爆炸荷载下的破坏形态如图10所示。L形柱破坏位置主要分布在柱底、梁柱节点与柱中部，随着剪跨比的减小柱中部破坏逐渐消失；T形柱破坏区域主要分布在柱底与梁柱节点处，随着剪跨比的减小柱破坏程度逐渐降低；相对于其余2种截面的异形柱，十字形柱破坏程度最低，仅在柱底部位出现少量的裂缝。

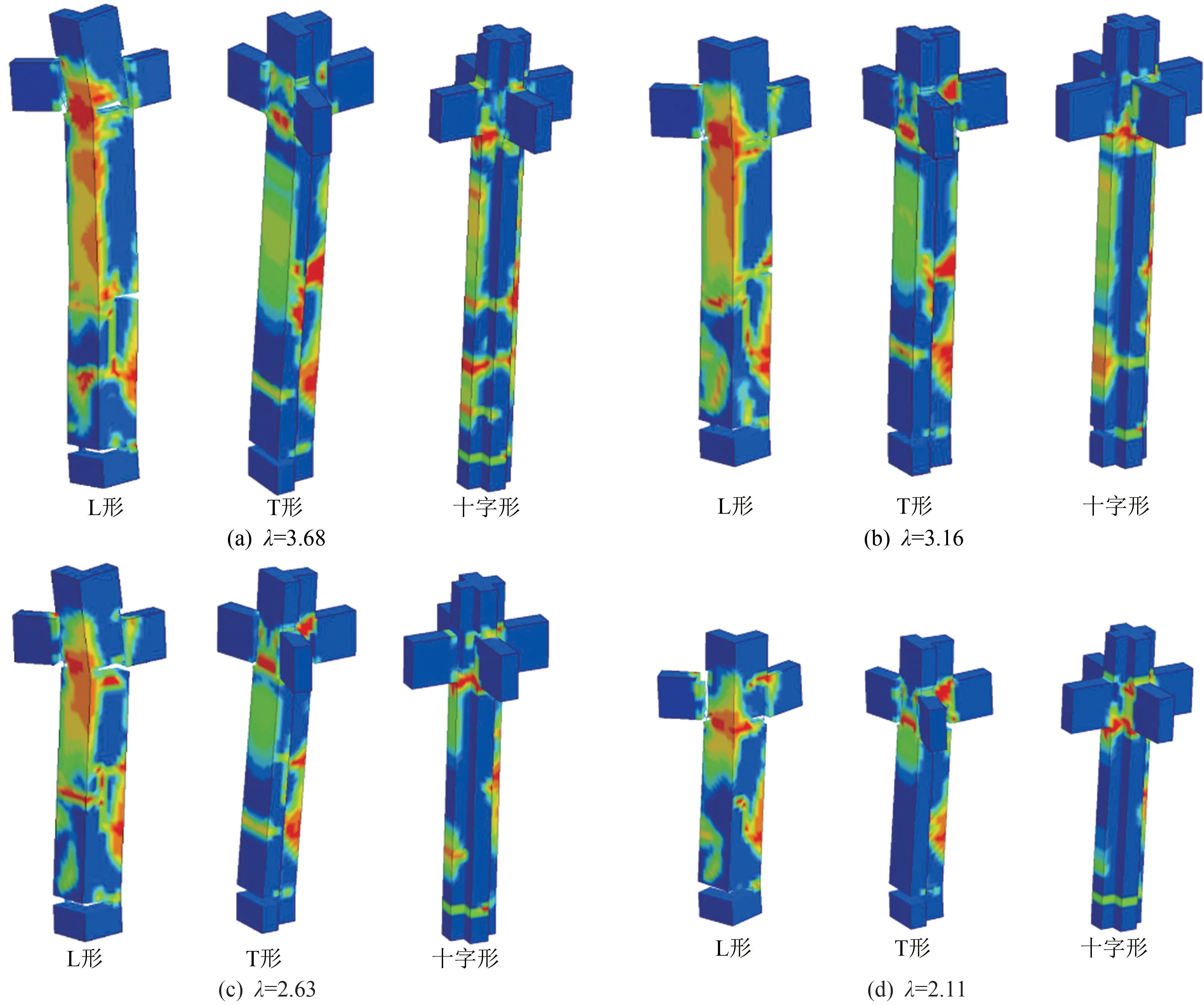
图10 爆炸荷载下不同剪跨比的RC异形柱破坏形态图

3.2.1 爆炸荷载下不同剪跨比的RC异形柱柱中位移动态响应分析

不同λ异形柱在Z为爆炸荷载下的柱中位移时程曲线如图11所示。爆炸荷载下不同剪跨比的异形柱均沿爆炸波方向产生水平位移，L形、T形柱位移接近且远大于十字形柱。剪跨比对L形、T形柱柱中位移影响较小，当λ由3.68减小为2.11时，其柱中截面位移仅减小5.8%、10.7%；剪跨比对十字形柱柱中位移影响较大，当λ由3.68减小为2.11时，其柱中截面位移减小82.5%。

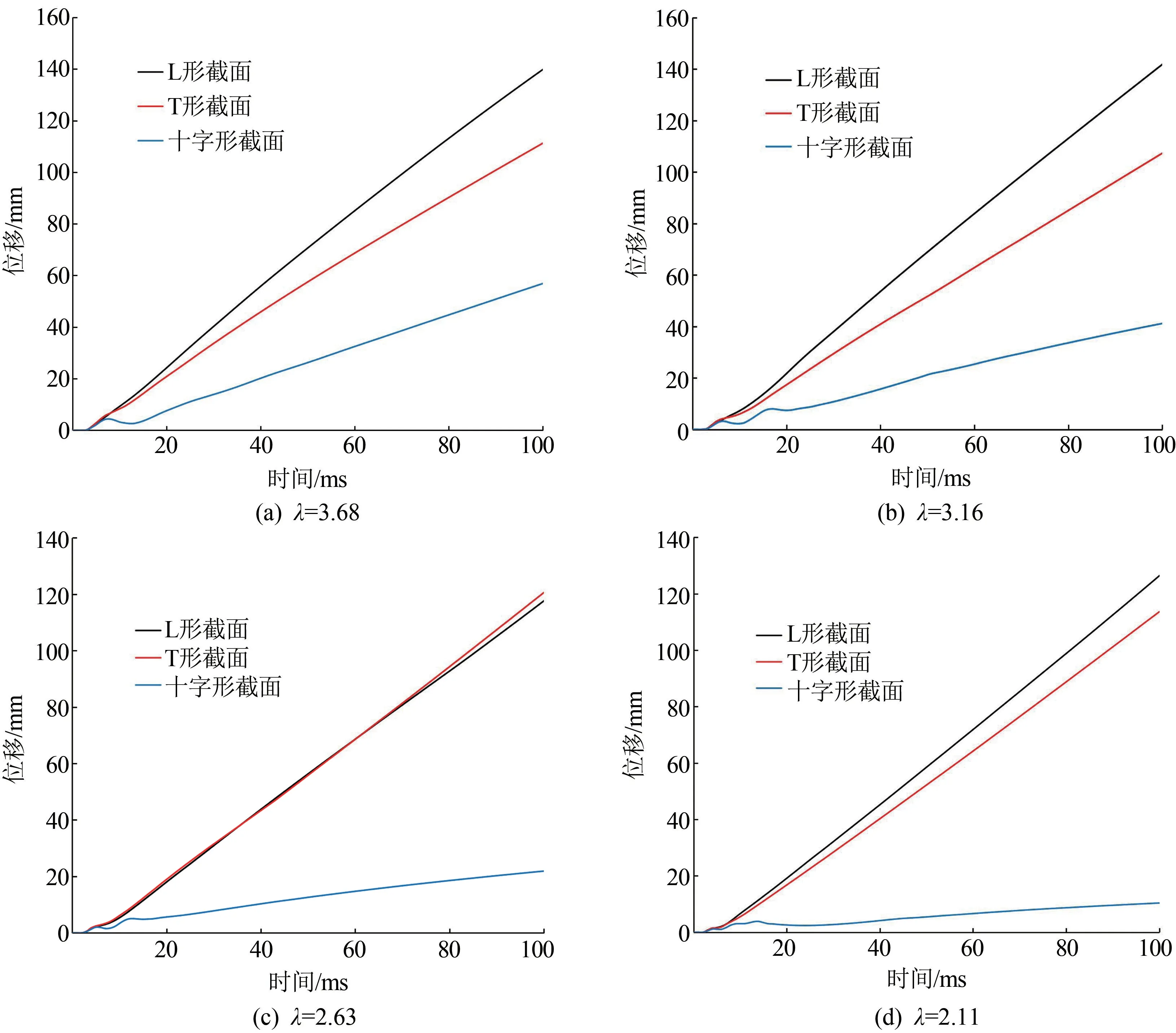
图11 爆炸荷载下不同剪跨比RC异形柱柱中位移时程曲线图

3.2.2 爆炸荷载下不同剪跨比的RC异形柱的柱底内力分析

不同λ的异形柱在Z为爆炸荷载下的柱底内力汇总见表4。

表4 爆炸荷载下不同剪跨比各柱柱底内力汇总表

根据表4分析可知，柱底轴力与弯矩均随着剪跨比的减小而减小。各柱柱底的偏心距随着剪跨比的减小而略有减小，λ＝2.11时3种不同异形柱柱底截面偏心距均稳定在0.5 m。除T形柱在λ＝3.68时偏心距略高以外，其余各柱随着剪跨比的变化偏心距一直在0.5～0.6 m的范围内。从破坏形态来看，各柱均表现出大偏心受压的特征，柱底迎爆面的混凝土发生受拉破坏，随着剪跨比的减小破坏程度降低。

4 结论

采用数值分析方法，借助LS-DYNA软件对爆炸荷载作用下不同轴压比与剪跨比RC异形柱的动力响应与柱底内力进行了分析，主要得到以下结论:

(1)随着轴压比的增加，L形、T形柱发生严重的破坏而十字形柱破坏程度较小，柱底受力特征由大偏心受压逐步转变为小偏心受压。随着剪跨比的减小，柱底迎爆面的混凝土发生受拉破坏程度降低。

(2)随着剪跨比的减小，L形、T形柱柱中位移较大而十字形柱明显减小。各柱柱底截面偏心距在0.5～0.6 m的范围内，受力特征始终保持为大偏心受压。当柱接近短柱(λ＝2.11)时，各柱的偏心距均为0.5 m。综合分析，十字形柱的抗爆性能优于L形柱与T形柱。

(3)提出的RC柱改进后的计算模型考虑了梁柱节点与柱顶水平位移的影响，能够较为准确地模拟柱在爆炸荷载作用下的真实状态。但该模型仅建立了梁柱节点附近的部分长度(500 mm)框架梁模型并设置为梁端固定约束，而实际与梁柱节点相连的框架梁全长均会发生变形并对梁柱节点产生影响。所以，与梁柱节点相连的框架梁长度具体数值、梁端约束形式需进一步研究。