一种改进的半监督集成软件缺陷预测方法

周建含,李英梅,李文昊

(哈尔滨师范大学 计算机科学与信息工程学院,哈尔滨 150000)

1 引 言

软件缺陷是编程人员在编码过程中因开发过程管理不当,难以正确理解软件需求、或者开发经验欠缺等原因产生的[1].软件缺陷对软件的生产带来负面的影响,会浪费大量的财力人力,因此,项目主管会在软件部署前通过软件测试等手段尽可能地找出软件中存在的缺陷,但是对所有的软件模块进行测试将是一项巨大的工程,可能会超出软件开发预算或延误软件发布时间.软件缺陷预测技术可以根据软件的历史数据信息,通过机器学习等方法来预测软件模块中是否含有缺陷,从而对可能含有缺陷的模块投入足够的测试资源[2].

目前,许多研究人员通过有监督机器学习建立起了很多性能优越的软件缺陷预测模型[3-8]但是,由于各种现实原因,很多时候无法获取到足够的标记模块信息.在这种带标记模块有限,未标记模块充足的情况下,使用有监督机器学习建立的软件缺陷预测模型往往不能取得较好的预测结果[9].因此,一些研究人员利用半监督机器学习建立了软件缺陷预测模型[10-14],来缓解标记样本匮乏的问题.但很少有研究考虑解决类不平衡和特征冗余、不相关问题对半监督软件缺陷预测模型带来的影响.因此本文分别在解决半监督缺陷预测模型的类不平衡和特征冗余、不相关问题上对多种方法进行了实验分析,最终在监督集成学习算法Tri-training的基础上提出一种改进的半监督集成软件缺陷预测方法FeSSTri.

FeSSTri是个两阶段算法:

1)对目标数据集中的标记样本使用ADASYN自适应综合过采样算法进行采样,通过增加少数类样本,使少数类样本规模与多数类样本规模达到一致,来解决半监督缺陷预测模型中的类不平衡问题.

2)利用标记样本结合采样后的半监督预测结果,使用最小冗余最大相关mRMR算法对目标数据集进行特征选择,得到最优的特征子集,解决特征冗余、不相关问题.

最后,利用采样后以及特征选择后的训练集使用Tri-training算法构建最终的预测模型.

本文在NASA数据集和AEEEM数据集上对FeSSTri算法进行了验证,在标记模块数量较少的情况下,相较于普通的Tri-training算法和经典的机器学习算法,FeSSTri可以取得更好的预测结果.

2 相关研究

软件缺陷预测的领域中有标记样本的数量与未标记样本的数量相比微乎其微,典型的有监督学习方法难以建立有效的预测模型,并且获得大量有标记样本的费用十分昂贵,而与有监督学习方法不同,半监督学习方法能同时利用少部分有标签样本和大部分没有标签的样本进行学习,解决了实际环境中有标记样本难以获取的问题,增强了分类模型的准确性.

2.1 半监督软件缺陷预测研究

Seliya等人基于期望最大化EM(Expectation-Maxi-mization)算法建立半监督预测模型,实验证明,该模型提高了预测的泛化性能[15].Catal等人利用半监督学习算法YASTI(Yet Another Two-Sta-ge Idea)构建了软件缺陷预测模型,并在YASTI算法的第一阶段对多种机器学习算法进行了实验,实验表明利用朴素贝叶斯算法构建的YASTI半监督软件缺陷预测模型效果最好.Lu等人提出了一种半监督软件缺陷预测模型FTF(Fitting The Fits),FTF第一步为全部未标记的实例设置标签,然后迭代训练模型直到未标记实例的预测结果趋于稳定,实验结果证明FTF在标记数据有限的情况下可以有效提高随机森林的预测结果[16].Lu HH等人提出了一种半监督降维学习的软件缺陷预测方法,是自训练算法FTcF(Fitting-the-confifident-Fits)的变体,通过利用标记样本反复进行训练,在每次迭代中对未标记样本进行预测,并且在降低软件度量的维度复杂性方法中嵌入了一个预处理策略,实验结果表明在降维之后半监督学习的预测效果显著优于随机森林算法[17].通过上述研究可以发现,在标记样本有限、未标记样本充足的情况下使用半监督学习算法构建软件缺陷预测模型的效果会更好,但是上述研究都很少考虑到类不平衡问题对半监督软件缺陷预测带来的影响.

针对半监督软件缺陷预测中的类不平衡问题,Ma等人提出一种基于半监督集成学习算法Tri-training的软件缺陷预测模型RusTri,通过对多数类样本作随机抽样的方法,使得Tri-training每次迭代更新的训练数据集达到类间平衡,实验证明,RusTri可以有效提升Tri-training的预测效果[9].张肖等人提出一种半监督集成软件缺陷预测方法Tri_Adaboost,通过欠采样和集成学习算法Adaboost来解决类不平衡问题的影响.Tri_Adaboost首先对标记样本进行欠采样,利用Tri-training算法扩充标记样本,然后利用已标记样本使用Adaboost算法构建最终的预测模型[2].上述研究的实验结果表明基于Tri-training算法构建的半监督软件缺陷预测模型效果非常好,但是上述研究都是利用欠采样方法来解决类不平衡对Tri-training算法的影响.在软件缺陷数据集中,有缺陷模块只能占到总体数目的10%-20%,如果使用欠采样方法训练数据集,使多数类样本减少到少数类样本数目,会丢弃大量宝贵的标记样本信息.因此,本文在采样阶段使用ADASYN自适应综合过采样算法来解决类不平衡对Tri-training算法的影响.

2.2 软件缺陷预测的特征选择研究

特征选择可以消除冗余特征和无关特征,从而得到良好的特征子集达到降维的效果,使模型泛化能力更强并有效提高分类模型的分类效果[18-20].Wang 等人借助集成学习方法来提高特征选择的性能[21].Menzies等人基于信息增益利用前向搜索和穷尽搜索来寻找最优特征子集[22].Song等人在缺陷预测框架中考虑了包裹式特征选择方法[23].Shivaji 等人在基于代码修改的软件缺陷预测中对各种特征选择方法进行了实验[24].Gao等人对多种过滤式特征选择方法在不同的子集评估策略上进行了实验对比[25].

但是目前在软件缺陷预测中常用的过滤式特征选择方法主要依据特征与标签列的相关度来进行选择,很少考虑特征之间的相似性,因此选出的特征子集很容易出现冗余问题.Peng等人提出了一种滤波式的特征选择方法mRMR(Max-Relevance,and Min-Redundancy)可以找出最小冗余最大相关的特征子集[26].因此,本文在半监督软件缺陷预测中对mRMR算法进行了尝试并与经典的过滤式特征选择方法进行了对比.

虽然,特征选择在软件缺陷预测领域已经有了很多研究[27],但很少有研究考虑到提出的方法在半监督软件缺陷预测上的适应性.因此本文提出一种应用在半监督软件缺陷预测上的特征选择框架,可以充分利用标记样本和未标记样本的信息.首先,利用采样后的半监督分类器可以建立一个有效的半监督缺陷预测模型,使用该模型对未标记样本进行预标记,然后对所有的已标记样本信息使用特征选择方法来对特征进行选择,实验证明在标记样本有限、未标记样本充足的情况下该框架可以有效提高特征选择方法的性能.

3 改进的半监督集成软件缺陷预测模型

3.1 研究动机

利用软件的历史缺陷信息以及相关度量,通过机器学习算法可以构建出有效的软件缺陷预测模型以此将足够的测试资源投入到可能存在缺陷的软件模块中.但是在实际环境中,由于软件模块的缺陷信息难以获取,常常面对标记模块有限、未标记模块充足的情况,因此构建一种稳定有效的半监督软件缺陷预测模型是非常有意义的.软件缺陷预测中的类不平衡、特征冗余和不相关问题会严重影响半监督软件缺陷预测模型的预测效果,因此本文基于采样和特征选择方法提出了一种改进的半监督集成软件缺陷预测方法FeSSTri来解决上述问题.

3.2 算法框架

图1、图2为FeSSTri算法的框架图,其中图1为FeSSTri算法得到最优特征子集的过程,图2为FeSSTri算法构建最终软件缺陷模型的过程.如图1所示,为了解决半监督缺陷预测的无关特征、冗余特征的问题,FeSSTri使用最小冗余最大相关mRMR算法进行特征选择,得到最优特征子集.但是由于初始标记样本数量很少,如果直接利用初始标记数据来进行特征选择只能获取到整体数据集的局部信息并且容易造成过拟合,降低软件预测模型的泛化性能.因此为了充分利用初始的标记样本和未标记样本的信息,本文提出了一种适应于半监督软件缺陷预测的特征选择框架.首先利用过采样后的标记样本使用Tri-training算法建立一个效果良好的半监督分类器,使用该分类器给未标记样本进行预标记,然后利用初始标记样本和预标记样本的信息进行特征选择.用上述方法寻找到的特征子集增强了分类器的泛化性能并且更加贴近原数据集的全局信息特点.

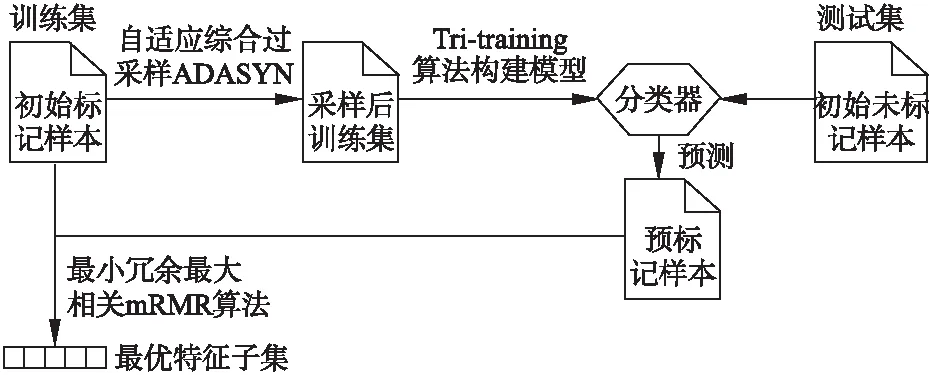
图1 FeSSTri算法过程1

如图2所示,在得到最优特征子集后,再将过采样后的标记样本根据最优特征子集进行特征选择,使用Tri-training算法构建最终的软件缺陷预测模型,最后用此模型对同样特征选择后的初始未标记样本进行预测,得出预测结果.

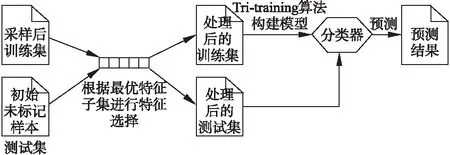
图2 FeSSTri算法过程2

3.3 采样阶段

软件缺陷预测中的类不平衡问题是指训练数据集中无缺陷样本的数目要远远大于有缺陷样本的数目.在这种情况下,如果直接使用机器学习算法构造分类器虽然可以较好地预测大类样本,但是无法对小类样本进行准确预测.软件缺陷数据集就存在着严重的类不平衡问题,有缺陷样本往往只能占到数据集的10%-20%,所以解决类不平衡问题是构建软件缺陷预测模型的一个重要课题.

采样方法是一种在数据层面上解决类不平衡问题的有效手段,通过采样可以使得数据集中各类别的样本数目达到一致.采样方法一般分为欠采样和过采样,欠采样减少了大量的大类样本,使其数目与小类样本达到一致,过采样则是增加小类样本的数目,使其数量与大类样本达到一致.在半监督软件缺陷预测模型的构建中,往往只能够获取到一个完整数据集10%-40%的标记样本数据而且里面的有缺陷样本更是少之又少,如果采用欠采样方法会丢失大量宝贵的标记样本信息.因此,采用过采样方法来解决半监督软件缺陷预测模型的类不平衡问题更加合理.

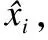
1)计算需要合成的样本总数量:

(1)

其中,Smaj为大类样本数量,Smin为小类样本数量,β∈(0,1)为系数,这里设为1即合成后小类样本数目与大类样本数目达到一致.

2)对于每个小类样本xi,找出其K个最近邻点,并计算:

(2)

其中,Δi为K近邻个点中大类样本的数量.

(3)

3)计算每个小类样本xi需要合成的样本数量gi,最后用SMOTE方法合成新样本:

(4)

由以上描述可知,在ADASYN算法中,小类样本周围的大类样本越多,则其周围生成的新样本就越多.这样生成的新样本大多都在分类边界处,可以提供有效的分类信息.ADASYN自适应综合过采样算法伪代码如下:

算法1.ADASYN自适应综合过采样算法

输入:初始标记样本集合S、小类样本近邻数目K

输出:过采样后的标记样本集合S′

1.Calculate the number of samples for large and small categories:Smaj、Smin;

2.Calculate the total number of samples to be generated:G=Smaj-Smin;

3.forXi∈Smin

4. Calculates the number of samples of large classes in K nearest neighbors:Δi

6.end for

7.forXi∈Smin

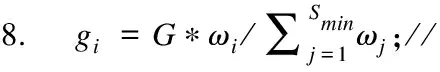
9. for 1:gi

10. Generate new samples:xnew=xi+(gi-xi)*δ,δ∈(0,1)

11. S′=S+xnew

12. end for

13.end for

14.return S′

3.4 特征选择阶段

软件工程师为了提高软件缺陷预测的准确性,增加了很多与软件缺陷密切相关的度量标准来度量程序模块,但是随着软件产品复杂度的增加,就会生成大量的特征值,导致了高维问题.使用特征选择可以从高维数据集中选出所含分类信息丰富的特征子集,降低数据集维度,提高预测模型的预测能力.一个优秀的特征子集有两大特点:1)具有很大的分类识别信息量,2)具有很强的独立性,因为特征间相关性太强难以提供多余的分类信息.在软件缺陷预测的研究中,过滤式特征选择是常用的方法,即选出与标签列相关性最大的特征,常用的相关性度量有距离相关系数、信息增益率、Pearson相关系数、卡方检验值等.上述方法都仅考虑了特征与分类变量之间的相关性而没有考虑到特征冗余问题,这就导致所选特征可能并不具备较好的独立性.

Peng等人提出一种最小冗余最大相关mRMR特征选择方法,该方法保证了所选特征和分类变量的相关度达到最高,而特征与特征之间的相关度最小.因此,采用mRMR方法更加合理.在mRMR中,互信息用来度量相关性,特征集S与标签列c的相关性是根据各个特征fi和标签列c之间的所有互信息值的平均值定义,如下所示:

(5)

集合S中所有特征的冗余由每个特征之间的所有互信息值的平均值定义:

(6)

mRMR方法定义如下:

(7)

mRMR方法根据已选择的特征,对剩下的候选子集中的特征进行计算并且排序,以便找到能使上述公式最大化的特征.这种搜索方法为增量搜索,目的是要找到最优特征子集.假设我们已有特征集Sm-1,那么接下来就是从剩下的特征F-Sm-1中找到第m个特征使得下式值最大:

(8)

基于mRMR的半监督软件缺陷预测特征选择方法伪代码如下:

算法2.最小冗余最大相关mRMR算法

输入:数据集S、特征集合F、特征选择数目K

输出:最优特征子集F′

1.set F′={};

2.set bestF=-1;

3.set bestScore=0;

4.for x in 1:K

5. forfj∈F

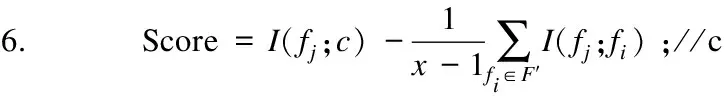
7. if Score>bestScore

8. bestScore=Score;

9. bestF=fj;

10. end if

11. end for

12. F′=F′+fj;

13. F=F-fj;

14.end for

15.return F′

3.5 利用Tri-training算法构建半监督软件缺陷预测模型

Tri-training算法是非常强大的半监督集成学习方法,能够使用少量标记的数据来构建效果良好的分类器,可以很好的解决标记模块不足的问题.Tri-training算法首先对带有标记的数据进行3次随机抽样,以此训练出各不相同的分类器,之后对没有标记的数据作出预测.若两个分类器将一个未标记的样本预测为负类,而第3个分类器预测为正类,那么第3个分类器应该把这个样本当作负类学习,通过3个分类器相互通知,很容易地处理标记置信度估计问题.对3个分类器进行多次迭代训练直至结果趋于稳定,最后使用最大投票法对3个分类器进行集成学习.可是在有些情况下,多数票分类器的预测结果有可能是错误的,那么就会给少数票分类器引入噪音,但是Z.-H.Zhou 和 M.L[28]表明,在一定条件下,分类噪声率的增加可以由新标记样本的数量补偿.在本文中Tri-training算法的基分类器采用RandomForest分类器.

Tri-training算法、FeSSTri算法伪代码如下:

算法3.Tri-training算法

输入:标记数据集S、未标记数据集U

输出:未数据集U的预测结果Y(U)

1.Bootstrap(S)→S1′,S2′,S3′;

2.RandomForest(S1′),RandomForest(S2′),RandomForest(S3′)→h1,h2,h3;

4.repeattrainingh1,h2,h3

5. for i in 1:3

6.ei←MeasureRrror(hj&hk)(j,k≠i)

8. usehjandhkto predict samples in U,append them into Si′;

9. end if

10.untilh1,h2,h3no longer change

11.retrun Y(U)=vote(h1(U),h2(U),h3(U));

算法4.FeSSTri算法

输入:初始标记样本集合S、初始未标记样本集合U、特征集合F、特征选择数目K

输出:未标记样本集合U的预测结果Y(U)

1.ADASYN(S,5)→S′;

2.Tri-training(S′,U)→U′;

3.L=S+U′

4.mRMR(L,F,K)→F′;

5.S*←FeatureselectionofS′ by F′;

6.U*←Featureselectionof U′ by F′;

7.Y(U)=Tri-training(S*,U*);

8.return Y(U);

4 实 验

4.1 实验设计

为验证FeSSTri方法在各阶段的有效性,设计了3组实验进行对比.

第1组实验验证ADASYN自适应综合过采样算法在采样阶段的有效性,选取随机欠采样、随机过采样、SMOTE过采样以及不做采样的Tri-training算法作为对比算法.

第2组实验验证本文提出的适应于半监督学习的特征选择框架的有效性,以及mRMR算法在特征选择阶段的有效性,选取基于信息增益率的过滤式方法、基于Pearson相关系数的过滤式方法、基于卡方检验值的过滤式方法以及不做特征选择的Tri-training算法作为对比算法.

第3组实验验证本文提出的FeSSTri方法在半监督软件缺陷预测上的有效性,选取J4.8、NaiveBayes、RandomForest、Tri-training算法作为对比算法.

上述实验数据均采用NASA数据集和AEEEM数据集,以F1值为实验评测指标.上述所有算法均基于python的sklearn工具包来实现.参照文献[9],将3组实验数据集的标记率设定为0.2,即随机选取数据集中的20%作为标记样本训练集,剩下80%的未标记样本作为辅助数据集和测试集.参照文献[29],将特征选择的数量设置为原始特征数目的40%.每组实验均随机选取10次标记样本,每次对各算法分别运行10次,取100次实验结果的平均值作为最终结果.

4.2 实验数据集

本研究使用了具有代表性的NASA数据集和AEEEM数据集[30-33],表 1和表2列出了这两个数据集的统计特征.

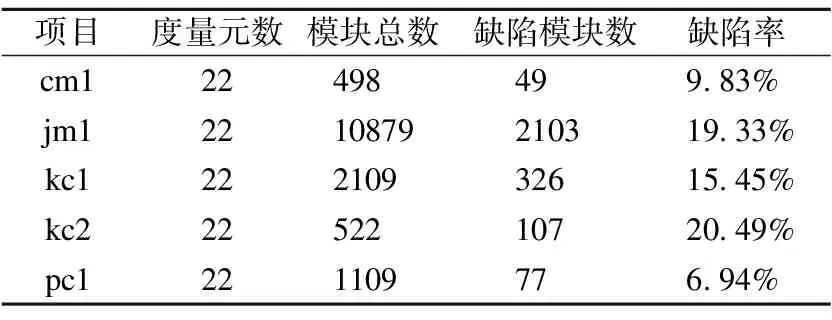
表1 NASA 数据集信息

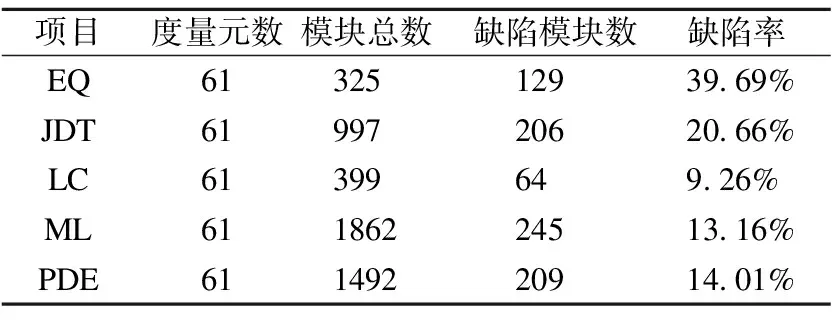
表2 AEEEM 数据集信息

NASA数据集在软件缺陷预测领域被广泛应用,因为NASA中的数据有很强的的真实性,提升了数据集的可信度.

AEEEM 数据集是由 D′Ambros 等人[33]搜集,他们分析了5个开源项目,从中收集到61种不同的度量元,这些度量元关注了代码复杂度以及软件的开发过程.

4.3 实验评测指标

软件缺陷预测是一个二分类问题,并且对于每个样本都有两个标记,一个是样本的真实类别,另一个是预测出来的类别,因此我们可以用混淆矩阵[34]中的数据来评估预测算法的性能.可能的结果如下:样本的真正标记是正,也被预测为正,记为 TP(true positive);样本的真正标记是正,但是被预测为负,记为FN(false negative);样本的真正标记是负,但是被预测为正,记为FP(false positive);样本的真正标记是负,也被预测为负,记为TN(true negative).通过这4种评估指标可以初次评估算法的性能,之后可以定义查准率(precision)、召回率(recall)以及F1度量(F1-measure).

1)查准率:在所有被预测为有缺陷的实例中,真实类别为有缺陷的实例所占的比例.

(9)

2)召回率:在所有真实类别为有缺陷的实例中,被正确预测为有缺陷的实例所占的比例.

(10)

3)F1度量:是一个综合评估数,是召回率和查准率之间的权衡.

(11)

查准率能得出检索到的缺陷模块有多少是准确的,召回率能得出模型是否能预测出有缺陷模块的能力.但是查准率和查全率是一对矛盾的度量,而F1是通过计算查准率和召回率的调和平均定义的,可以避免出现极端现象,能够得出合理的性能估计.基于以上原因,本文使用 F1 评价各方法的性能.

4.4 实验结果分析

4.4.1 采样阶段实验结果及分析

表3、表4为Tri-training算法经过不同采样算法后在NASA数据集和AEEEM数据集上的实验结果.由表3、表4可见,在缺陷模块较少的NASA数据集上,随机欠采样方法只有在项目cm、jm上可以略微改进Tri-training算法的预测结果,在其余项目上的预测结果均比初始Tri-training算法差;

表3 各采样方法在NASA数据集上的F1值

而在缺陷模块较多的AEEEM数据集上,随机欠采样方法只有在缺陷数目较少的项目LC上的预测结果低于初始Tri-training算法.说明当训练集所含的缺陷模块信息很少时,使用欠采样方法会丢失训练集中大量宝贵的标记模块信息从而使得训练后的预测模型性能降低.在表3、表4中可以看出随机过采样、SMOTE过采样、ADASYN自适应综合过采样方法在NASA和AEEEM两个数据集上均可以提升初始Tri-training算法的预测结果,其中ADASYN自适应综合过采样方法的提升最大,SMOTE方法次之,说明使用过采样方法解决半监督软件缺陷预测的类不平衡问题效果更好,使用ADASYN自适应综合过采样方法可以达到最好.

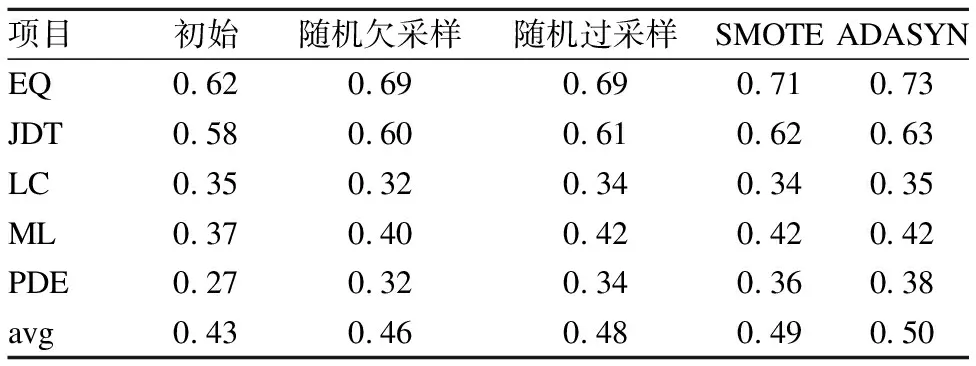
表4 各采样方法在AEEEM数据集上的F1值

4.4.2 特征选择阶段实验结果及分析

表5、表6为Tri-training算法经过不同特征选择方法后在NASA数据集和AEEEM数据集上的实验结果,其中括号里的数据为该特征选择方法在本文提出的适应于半监督学习的特征选择框架下的实验结果.由表5、表6可见,在两个数据集上本文提出的适应于半监督学习的特征选择框架可以提升基于信息增益率的过滤式方法、基于卡方检验值的过滤式方法以及最小冗余最大相关mRMR方法的预测结果,只有在基于Pearson相关系数的过滤式方法上会降低原方法的预测结果.其中,基于信息增益率的过滤式方法和基于卡方检验值的过滤式方法在使用该框架后才可以提升初始Tri-training算法的预测结果,说明本文提出的特征选择框架可以在标记模块有限的情况下充分利用未标记模块的信息使得特征选择方法更加有效.

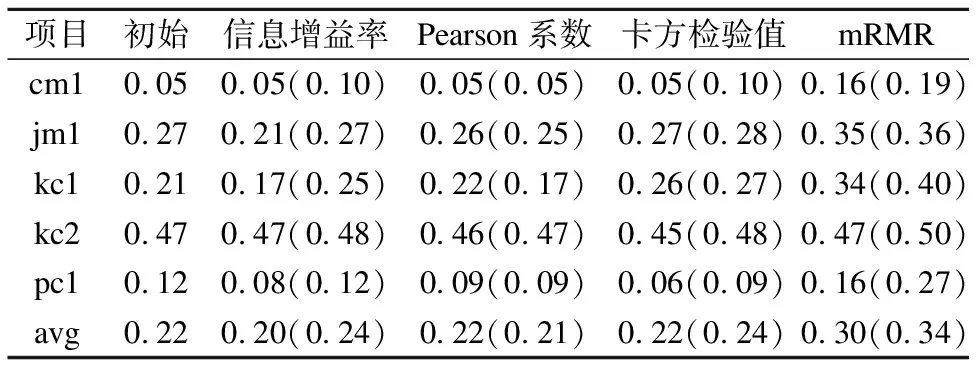
表5 各特征选择方法在NASA数据集上的F1值

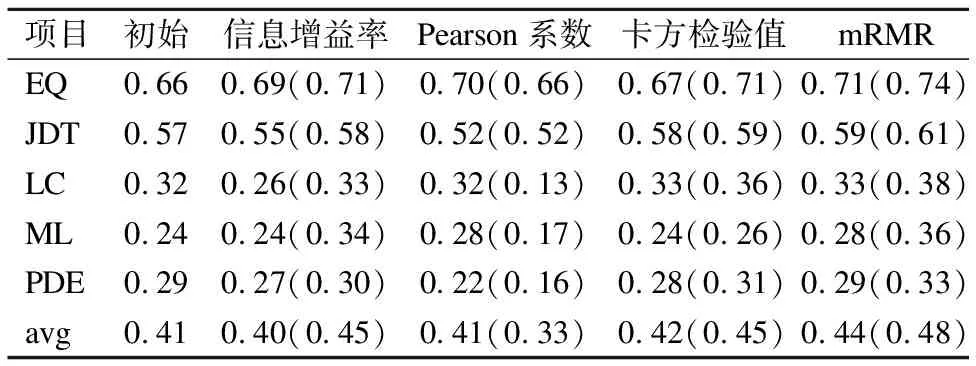
表6 各特征选择方法在AEEEM数据集上的F1值

由表5、表6可见在本文提出的特征选择框架下,基于信息增益率的过滤式方法、基于卡方检验值的过滤式方法以及最小冗余最大相关mRMR方法均可以提升初始Tri-training算法的预测结果,其中最小冗余最大相关mRMR方法的提升效果最大,说明mRMR方法在软件缺陷预测的特征选择阶段更加有效.

4.4.3 FeSSTri实验结果及分析

图3、图4为NASA数据集和AEEEM数据集上的各分类模型在0.2标记率下的平均实验结果.由图3、图4可见,在两个数据集上本文提出的FeSSTri方法可以有效提高Tri-training算法的预测结果,并且比起J48、NaiveBayes、RandomForest等算法也可以取得最佳的预测结果.在NASA数据集上,FeSSTri与其他4种经典算法相比,性能可以提升36%、41%、45%、18%;在AEEEM数据集上,FeSSTri与其他4种经典算法相比,性能可以提升40%、27%、22%、14%.由此可说明,结合了ADASYN自适应综合过采样方法和最小冗余最大相关mRMR方法的FeSSTri是一种有效的半监督软件缺陷预测模型.

图3 各方法在NASA数据集上的F1平均值

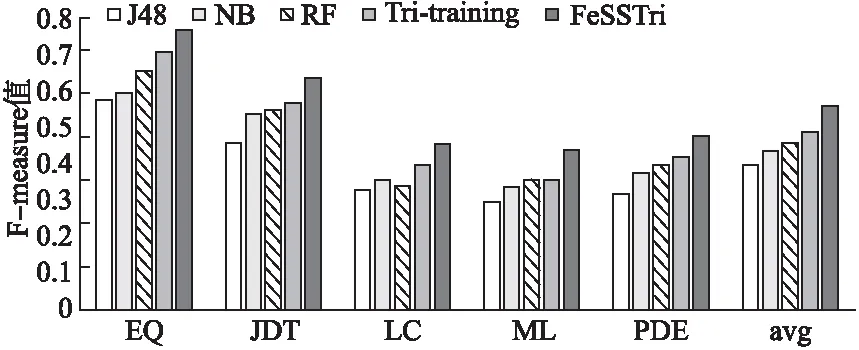
图4 各方法在AEEEM数据集上的F1平均值

5 结束语

为了进一步提升半监督软件缺陷预测模型的性能,本文提出一种半监督集成软件缺陷预测方法FeSSTri,采用ADASYN自适应综合过采样算法以及最小冗余最大相关mRMR算法来解决半监督软件缺陷预测中的类不平衡和特征冗余、不相关问题.实验表明,FeSSTri方法可以在采样阶段和特征选择阶段最大化提升基于Tri-training算法的半监督软件缺陷预测模型的效果,并且比起经典的机器学习算法在标记样本不足的情况下可以取得更好的预测结果.下一步工作主要探究特征选择的数量对软件缺陷预测模型的影响以及包裹式特征选择方法在半监督软件缺陷预测模型中的应用.