颗粒物料垂直管道水力输送阻力计算方法探讨

王锋 ，何炎平 ，3*，李铭志 ，刘炜煌 ，陈芊屹

（1.上海交通大学海洋工程国家重点实验室，上海 200240；2.上海交通大学船舶海洋与建筑工程学院，上海 200240；3.高新船舶与深海开发装备协同创新中心（船海协创中心），上海 200240）

0 引言

海底矿产资源丰富，如铁锰结核、钴锰结壳、多金属硫化物等，是未来人类开发利用有价金属（铜、锰、镍、钴、稀土金属等）的重要原料来源[1]。管道输送具有安全性好、经济成本低和环境破坏小等优点[2]，因此，垂直管道水力提升被认为是最适合深海海底矿产资源向海面输送的一种方式。

深海矿产水力提升涉及复杂介质的两相流问题[3]，由于颗粒与水、颗粒与管壁、甚至颗粒与颗粒之间复杂的能量交换，管道阻力准确计算至今仍然是一大难题[4]。但是，管道输送阻力计算的准确性对整个输送系统设计、施工方案设计等工作都影响非常显著。例如，在系统设计阶段，如果计算值偏大，据此选择的动力系统会偏大，显然会带来资源的浪费，经济上不实惠；计算值偏小会造成工程生产的不可靠[5]。然而，相对于颗粒物料水平管道输送阻力计算的研究成果，垂直管道输送阻力计算的相关研究成果较少。

针对颗粒物料垂直输送，很多学者贡献了优秀的研究成果。典型的有，我国学者王绍周基于能量理论提出的垂直管道输送阻力计算公式[6]；夏建新做了大量锰结核垂直管道输送实验研究，给出了考虑摩擦、位移和附加损失的管道阻力计算方法[7]；Matousek 基于颗粒粒径提出了3 种不同粒径范围颗粒的垂直管道阻力计算公式[8]。但是，受到实验条件的限制，各位学者的阻力计算模型都只是在自己所做实验范围内得到了准确性验证。本文引用夏建新锰结核试验数据、Vlasak 锰结核垂直管道输送试验数据和Matousek 泥沙垂直管道输送试验数据，将王绍周、夏建新和Matousek 公式计算结果与实验测量值相比较，探讨各公式在不同工况条件下的计算准确性，供颗粒物料垂直管道输送系统设计和施工计算参考。

1 典型计算方法

1.1 王绍周公式

王绍周认为垂直管道中颗粒物料浆体的摩阻损失im与物料的平均沉降速度、浆体输送平均速度v 等因素有关。具体表达如式（1）[6]：

式中：Cv为颗粒体积浓度；D 为管径；ρ为液体密度；ρm为浆体密度；ρs为颗粒密度；Sm为浆体与水的密度比，由式（2）计算得到：

α为减阻系数，可由浆体相对黏度μr计算得到：

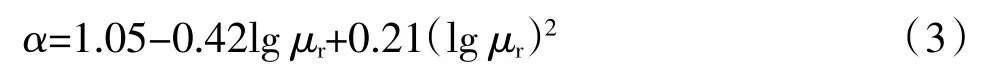
λ为达西摩阻系数，可由雷诺数Re 计算得到：

式中：ε为浆体管道的绝对粗糙度。

1.2 夏建新公式

夏建新等人把固液两相流在垂直管中运动时压力损失分为3 部分[7]，包括：1）载体与管壁的摩擦损失；2）提升物料位能损失；3）附加压力损失，包括颗粒间的碰撞及颗粒与边界碰撞。垂直管道中颗粒输送的压力损失im′用式（5）计算[7]：

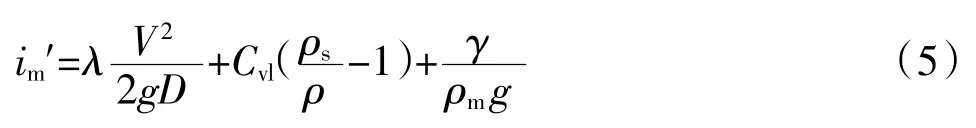
式中：Cvl为管道中的局部颗粒体积浓度，用式（6）计算：

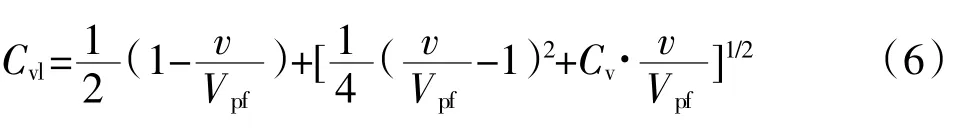
式中：Vpf颗粒群滑移速度；γ为颗粒碰撞次数与每次碰撞的能量损失的乘积。

1.3 Matousek 公式

Matousek 认为垂直管道中颗粒物料浆体的沿程压降是由流动边界层中颗粒与颗粒间的相互作用、颗粒与液体间的相互作用造成的，主要是颗粒与液体之间的相互作用有关[8]。Matousek 为了提高计算的准确性，在计算垂直管道中颗粒物料浆体摩阻损失时，将颗粒细分为粗砂、中砂和细砂3 种，具体表达如式（7）~（9）：

粗砂管道输送摩阻损失计算公式：

中砂管道输送摩阻损失计算公式：

细砂管道输送摩阻损失计算公式：

式中：if为清水摩阻损失。

2 计算结果与实测值比较

选取夏建新等人试验工况、Vlasak 等人试验工况和Matousek 试验工况，运用3 种典型计算方法，分别采用实验平均流速和平均浓度作为计算流速和计算浓度，采用实验物料颗粒中值粒径为计算颗粒粒径，计算各工况下输送浆体的摩阻损失，与实验值比较，对比不同工况下各计算方法的准确性。

2.1 夏建新等人试验工况对比分析

夏建新等人试验工况参数如下：实验研究对象为锰结核，实验物料用等直径球形颗粒代替锰结核，密度为2 000 kg/m3，球形颗粒粒径为15 mm，颗粒体积浓度范围在0.05~0.25 之间。垂直管输送管径为100 mm，管壁为钢材，管壁相对粗糙度约为0.001 1。

王绍周公式、夏建新公式、Matousek 公式计算得出的摩阻损失计算值和夏建新等人试验工况实测值对比见图1。

图1 公式计算值与夏建新实测值对比图Fig.1 Comparison diagram of formula calculated value and XIA Jian-xin experimental results

如图1 所示，当颗粒体积浓度为0.05 时，王绍周公式计算值与夏建新等人试验工况实测值偏差较小；当颗粒体积浓度为0.25 时，王绍周公式计算值与实测值偏差较大。在不同流速不同浓度条件下，夏建新公式计算值与夏建新等人试验工况实测值数值偏差较小。Matousek 公式计算值与夏建新等人试验工况实测值偏差较小。

2.2 Vlasak 等人试验工况对比分析

Vlasak 等人试验工况[9]参数如下：实验物料为粒径分布较窄的玄武岩卵石组成，粒径范围为8~16 mm，颗粒中值粒径为11 mm，颗粒密度为2 787 kg/m3，颗粒体积浓度范围在0.05~0.14 之间。垂直管输送管径为100 mm，管壁为钢材。

王绍周公式、夏建新公式、Matousek 公式计算得出的摩阻损失计算值和Vlasak 等人试验工况实测值对比见图2。

图2 公式计算值与Vlasak 实测值对比图Fig.2 Comparison diagram of formula calculated value and Vlasak experimental results

如图2，在平均流速小于2.8 m/s 时，王绍周公式计算值远小于Vlasak 等人试验工况实测值；但当平均流速逐渐增大时，计算值与实测值偏差减小。在低平均流速时，夏建新公式计算值与Vlasak 等人试验工况实测值偏差较小；但随着流速的增大，计算值与实测值偏差增大。Matousek公式计算值与Vlasak 等人试验工况实测值总体偏差较小。

2.3 Matousek 试验工况对比分析

Matousek 试验工况参数如下：实验物料为粒径分布较窄的砂，密度为2 000 kg/m3，颗粒中值粒径为1.84 mm。垂直管输送管径为150 mm，管壁为钢材。

计算浓度采用实验平均浓度，Matousek 实验浓度范围为0.07~0.14 和0.32~0.39，计算浓度采用 0.105 和 0.355。

王绍周公式、夏建新公式、Matousek 公式计算得到的摩阻损失计算值和Matousek 试验工况实测值对比见图3。

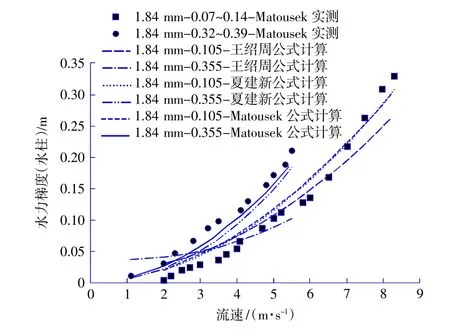
图3 公式计算值与Matousek 实测值对比图Fig.3 Comparison diagram of formula calculated value and Matousek experimental results

如图3 所示，颗粒体积浓度在0.07~0.14 范围内，当平均流速低于4 m/s 时，王绍周公式计算值与Matousek 试验工况实测值偏差较大；当平均流速在4.0~5.5 m/s 之间时，偏差较小。颗粒体积浓度在0.32~0.39 范围内，王绍周公式计算值与Matousek 试验工况实测值偏差较大。颗粒体积浓度在0.32~0.39 范围内，夏建新公式计算值偏小于实测值。颗粒体积浓度在0.07~0.14 范围内，当平均流速小于7 m/s 时，夏建新公式计算值与实测值偏差较大；当平均流速大于7 m/s 时，偏差较小。颗粒体积浓度0.105、流速小于7 m/s 时，Matousek 公式计算值偏大于实测值；除此之外，Matousek 公式计算值与实测值在不同浓度和不同流速条件下偏差均较小。

3 分析与讨论

3.1 王绍周公式

图4 给出了王绍周公式摩阻损失计算值与3组工况实测值的偏差。

图4 王绍周计算值与3 组实测值偏差图Fig.4 Deviation diagram of WANG Shao-zhou calculated value and three sets of experimental results

如图4 所示，粒径为15 mm 的粗颗粒，颗粒体积浓度在0.05~0.13 范围内，计算值与实验值偏差小于10%；颗粒体积浓度为0.25 时，偏差大于20%。粒径为11 mm 的粗颗粒，在低流速条件下，计算值与实测值偏差都大于20%；流速达到3 m/s后，偏差小于10%。粒径为1.84 mm 的颗粒，计算值与实验值偏差大于20%，摩阻损失计算结果不准确。

3.2 夏建新公式

图5 给出了夏建新公式摩阻损失计算值与3组工况实测值的偏差。

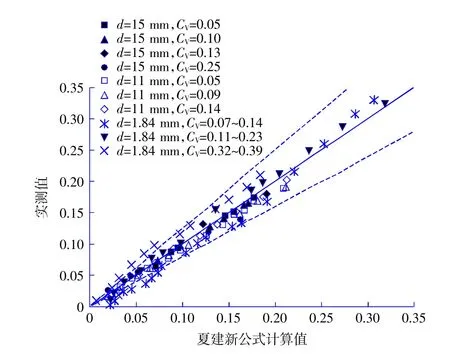
图5 夏建新计算值与3 组实测值偏差图Fig.5 Deviation diagram of XIA Jian-xin calculated value and three sets of experimental results

如图5 所示，粒径为15 mm 的粗颗粒，夏建新计算值与3 组实测值偏差小于5%。粒径为11 mm 的粗颗粒，夏建新计算值与3 组实测值偏差小于10%。粒径为1.84 mm 的颗粒，在低流速条件下，偏差大于20%；流速达到7 m/s 后，偏差小于20%。

3.3 Matousek 公式

图6 给出了Matousek 公式摩阻损失计算值与3 组工况实测值的偏差。

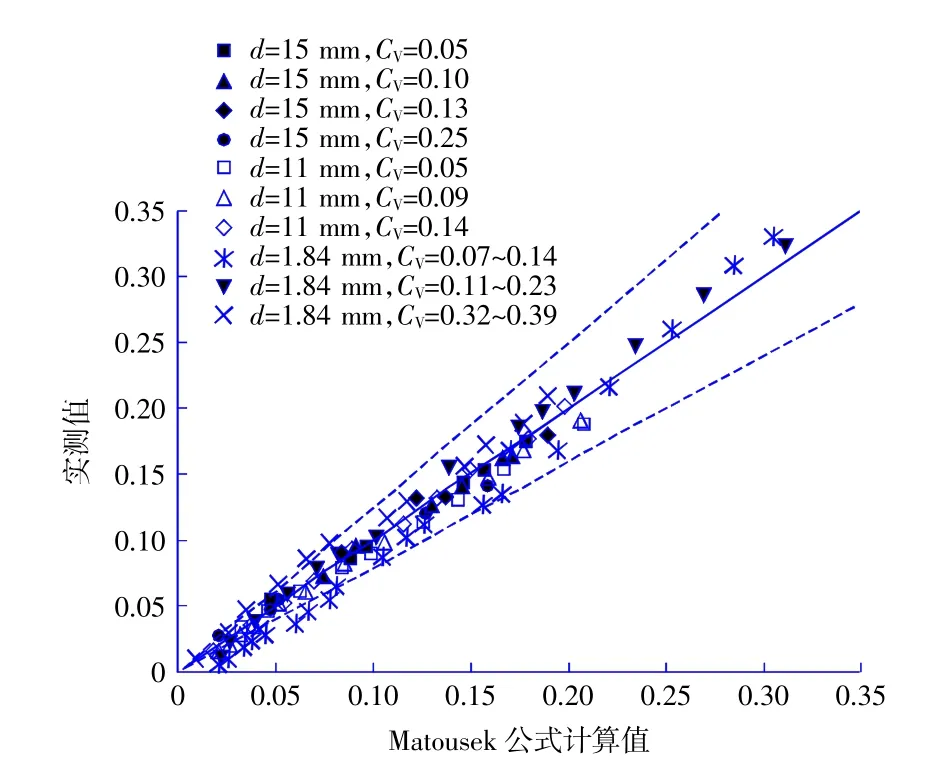
图6 Matousek 计算值与3 组实测值偏差图Fig.6 Deviation diagram of Matousek calculated value and three sets of experimental results

如图6，粒径为15 mm 的粗颗粒，Matousek计算值与3 组实测值偏差小于5%。粒径为11 mm的粗颗粒，Matousek 计算值与3 组实测值偏差小于5%。粒径为1.84 mm 的颗粒，在低流速条件下，偏差较大；流速达到7 m/s 后，偏差小于10%。对比图5 与图6 可知，Matousek 公式计算值与实测值偏差小于夏建新公式计算值与实测值偏差。这是因为Matousek 将颗粒细分为粗砂、中砂和细砂3 种，分别给出具体计算公式，则在流速高于沉降速度后，Matousek 公式对中粗颗粒摩阻损失计算更加准确。

4 结语

本文介绍了3 种典型的垂直管道摩阻损失计算公式，通过公式计算结果与实验测量结果的对比分析，讨论不同工况条件下各垂直管道摩阻损失计算公式的适用性。主要结论如下：

1）对于粒径在1.84~15 mm 范围内、浓度在0.05~0.39 范围内的颗粒物料垂直管道输送摩阻损失计算，Matousek 公式计算结果比较准确，偏差在10%以内。

2） 对于粒径在11~15 mm 范围内、浓度在0.05~0.25 范围内的颗粒物料垂直管道输送摩阻损失计算，Matousek 公式和夏建新公式计算结果都比较准确，偏差在5%以内。

3）本文探讨了颗粒粒径在1.84~15 mm 范围内、浓度在0.05~0.355 范围内的摩阻损失计算准确性，对于超出该范围的摩阻损失计算准确性还需进一步验证。