一种用于SCMA系统的混合期望传播检测方法*

张 毅，余 湋，王 瀚，高 航

(1.中国西南电子技术研究所,成都 610036;2.上海交通大学 电子工程系,上海 200240)

0 引 言

为了实现万物互联，下一代无线通信提出了很多新的技术挑战，包括高频谱效率、低延迟和大规模连接等[1]。为了解决这些挑战，多种非正交多址技术[1-3]被提出和研究。作为频域的非正交多址技术，稀疏码多址接入(Sparse Code Multiple Access，SCMA)技术用有限的频率资源实现了更多的连接[1]。作为低密度扩频码分多址(Low Density Signature-Code Division Multiple Access，LDS-CDMA)技术[4]的演进，SCMA直接结合了映射和扩频，即通过码本直接将二进制比特调制为高维码字。与LDS-CDMA技术相比，由于非线性操作的高维码本设计，这种方案允许SCMA技术获得高维星座图的整形增益。因此，一些文章[5-6]研究了SCMA的高维星座设计，通过星座的优化设计可以进一步提高系统容量。

在接收端，由于码本的稀疏性，SCMA技术通过稀疏因子图上的消息传递算法(Message Passing Algorithm，MPA)实现多用户检测，与最佳后验概率算法相比，该算法性能接近但复杂度较低[4]。为了降低MPA的复杂度，文献[4]提出了对数域MAX-Log MPA算法。但是，考虑到实际应用，MPA的复杂度仍然很高，尤其是在系统过载严重且码本很大的情况下。

为了解决MPA的复杂度过高问题，文献[7-15]提出了一些改进的MPA的检测算法。原始MPA在因子图的边上传递概率消息，直到达到最大迭代次数为止。文献[16]根据信道质量提出了一种低复杂度的MPA。它仅基于因子图上部分选择的边更新从功能节点传递到变量节点的消息，而未选择的边上的消息则通过均值反馈进行补偿。文献[10-11]提出了一种基于期望传播(Expectation Propagation，EP)的低复杂度MPA，它将因子图上的原始离散概率消息近似为连续的高斯分布。尽管与原始MPA相比，这些方法的复杂度有所降低，但性能损失却有些严重。 因此，平衡性能和复杂性对于SCMA的多用户检测至关重要。文献[17-19]基于MPA来进行检测，在计算当前符号的概率信息时将参与计算的部分其他符号视为高斯变量以减少计算复杂度。但是这些文章只在计算后验概率的节点时考虑了这种近似方式。

本文为了在性能和复杂性之间取得更好的折衷，充分利用信道信息，提出了一种混合期望传播检测方法用于SCMA检测。首先，对于因子图中某些信道质量较差的边，利用复高斯分布来近似其上的迭代信息，并将得到的均值和方差进行迭代传递。其次，建立混合期望传播算法的平均复杂度与信道阈值之间的关系。在实际应用中，这种关系可以基于信道阈值估计算法平均复杂度，因此基站可以通过不同用户的信道质量指示信息灵活地选择信道阈值来控制算法复杂度。最后，将混合期望传播检测方法与消息回退机制结合来加快检测算法的收敛并补偿由于降低复杂度而带来的性能损失。

1 SCMA系统模型

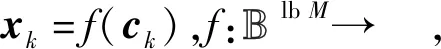
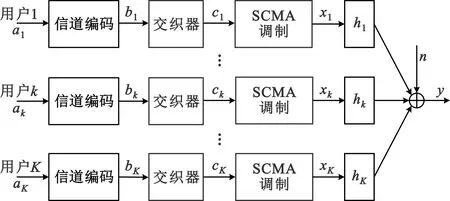
图1 SCMA系统的发送端模型

在接收机端，接收到的信号是K个经过衰落的用户信号与信道噪声的叠加。考虑无记忆瑞利衰落信道，则接收信号可以用离散形式表示：

(1)

对于SCMA系统，其稀疏特征由因子图表示。因子图不仅指示资源占用，而且直观地呈现了检测算法的迭代过程。如图2所示，从码本获得的因子图包含表示资源的功能节点Fn(n=1,2,…,N)和表示用户的变量节点Vk(k=1,2,…,K)。原始的MPA在此因子图中通过概率信息的多次迭代获得最终的检测结果。

图2 SCMA系统的因子图

2 瑞利衰落信道下的SCMA检测算法

2.1 混合期望传播检测算法

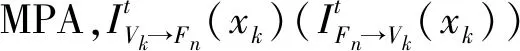
(2)

式中：Σ～xk表示对SCMA用户所有可能的码字组合(除了xk)进行求和，由信道接收的传输概率表示为

φn(xn)=(1/(πN0))exp(-(|yn-∑u∈∂nhn,uxn,u|2/N0)),

∂n表示连接到Fn的变量节点的集合，同时∂nk表示∂n去掉第k个节点后的集合。

在期望传播算法中，概率消息的分布由最小Kullback-Leibler散度(Minimum Kullback-Leibler Divergence,MKLD)准则来近似。具体地，MKLD准则用于获得p(w)的最佳近似值q(w)，表示为

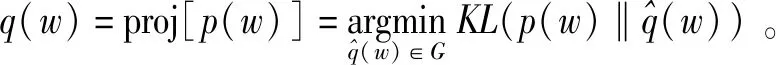
(3)

对于瑞利衰落信道，不同用户在不同时频资源上的信道状况是不同的，这导致在因子图边上迭代的概率消息的值有高有低。当边对应的信道质量良好时，该边上的概率消息集中在所发送的码字上；当边的信道质量差时，在该边上传递的概率信息相对平坦。因此，考虑用复高斯分布近似信道质量较差的边上的概率消息，从而每次仅需要传递均值和方差消息而不是多个码字的概率值消息。

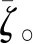
据此，功能节点与变量节点之间的信息更新如图3所示。

图3 混合期望传播检测流程图

(1)功能节点消息更新

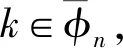
(4)

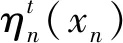
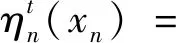
(5)

(6)

(7)

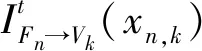
(8)

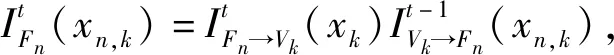
(9)

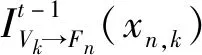
(10)

(2)变量节点消息更新

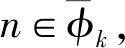
(11)

式中：分母Z是归一化参数。

(12)

2.2 边选择策略

对于所提出的混合期望传播算法，一方面，通过固定需要近似的边的数量来获得固定的复杂度检测算法；另一方面，通过信道阈值θth来控制算法复杂度。当信道阈值θth给定，衰落信道的信道系数的随机性会导致需要做近似的边的数量变成一个随机变量D，因子图中的总的边数为W。

对于瑞利频率平坦衰落信道，信道系数|hn,k|是瑞利分布的。因此，|hn,k|对应的边上的消息需要做近似的概率为

进一步，从W条边中挑出d条需要近似的边的概率为

(13)

因此，D的均值为

(14)

此时，信道阈值θth和变量D的均值E(D)之间的关系为

(15)

由2.1节可知，所提出的混合期望传播算法的平均复杂度和E(D)有关系，所以通过公式(15)就建立起了算法平均复杂度和信道阈值之间的关系。

在选择要近似的边时，有必要考虑信道的时变特性，即考虑基于信道阈值的边选择机制。可以通过算法平均复杂度来确定信道阈值的值。当因子图上的边对应的信道系数|hn,k|小于θth时，该边上的消息为近似后的复高斯分布的均值和方差消息。

2.3 消息回退机制

对于MPA，消息回退机制可以加快算法的收敛速度，即在第t次迭代中利用在第t次迭代中计算出的消息与在第t-1次迭代中传递的消息的凸组合来获得最终的传递消息。具体地，对于提出的混合期望传播算法，边上传递的消息形式有概率消息和均值方差消息两种。对于那些信道质量好的边，令It(xk)表示公式(4)和公式(11)中的计算得到的概率值，则在第t次传递的消息重新表示成

(16)

式中：α∈[0,1)是回退系数。对于那些信道质量差的边，令μt和τt表示式(10)和式(12)计算得到的均值和方差，则在第t次传递的均值和方差消息为

(17)

可以通过蒙特卡洛仿真获得α的最佳值，这将在下一节中给出。

3 性能仿真分析

3.1 仿真条件

系统可用资源数设置为N=4，用户数设置为K=6，调制阶数设置为M=4，因此系统的过载率为150%。仿真中使用的SCMA码本矩阵是规则的，同时功能节点的度(每个节点连接的边数)是df=3，从而W=N×df=12。信道编码采用LDPC码，LDPC码的码率设置为0.5，相应的校验矩阵大小设置为6 048×12 096。仿真信道为瑞利衰落信道。为了说明信道阈值对于混合期望传播算法的影响，仿真采用了两种信道阈值方案：

方案1：θth=1.2，根据公式(13)，对应于E(D)≈6，较少的边被近似。

方案2：θth=1.5，根据公式(13)，对应于E(D)≈8，较多的边被近似。

3.2 仿真结果与分析

图4给出了在混合期望传播算法下，不同通道阈值θth对应的误码率(Bit Error Rate,BER)随α的变化趋势。由图可知，方案1(信噪比3.5 dB)最优的(BER最小)回退系数为α=0.32,方案2(信噪比4 dB)最优的回退系数为α=0.38。因此，不同的信道阈值θth对应的最优回退系数α可以通过仿真出相应的BER和α的关系曲线来获得。

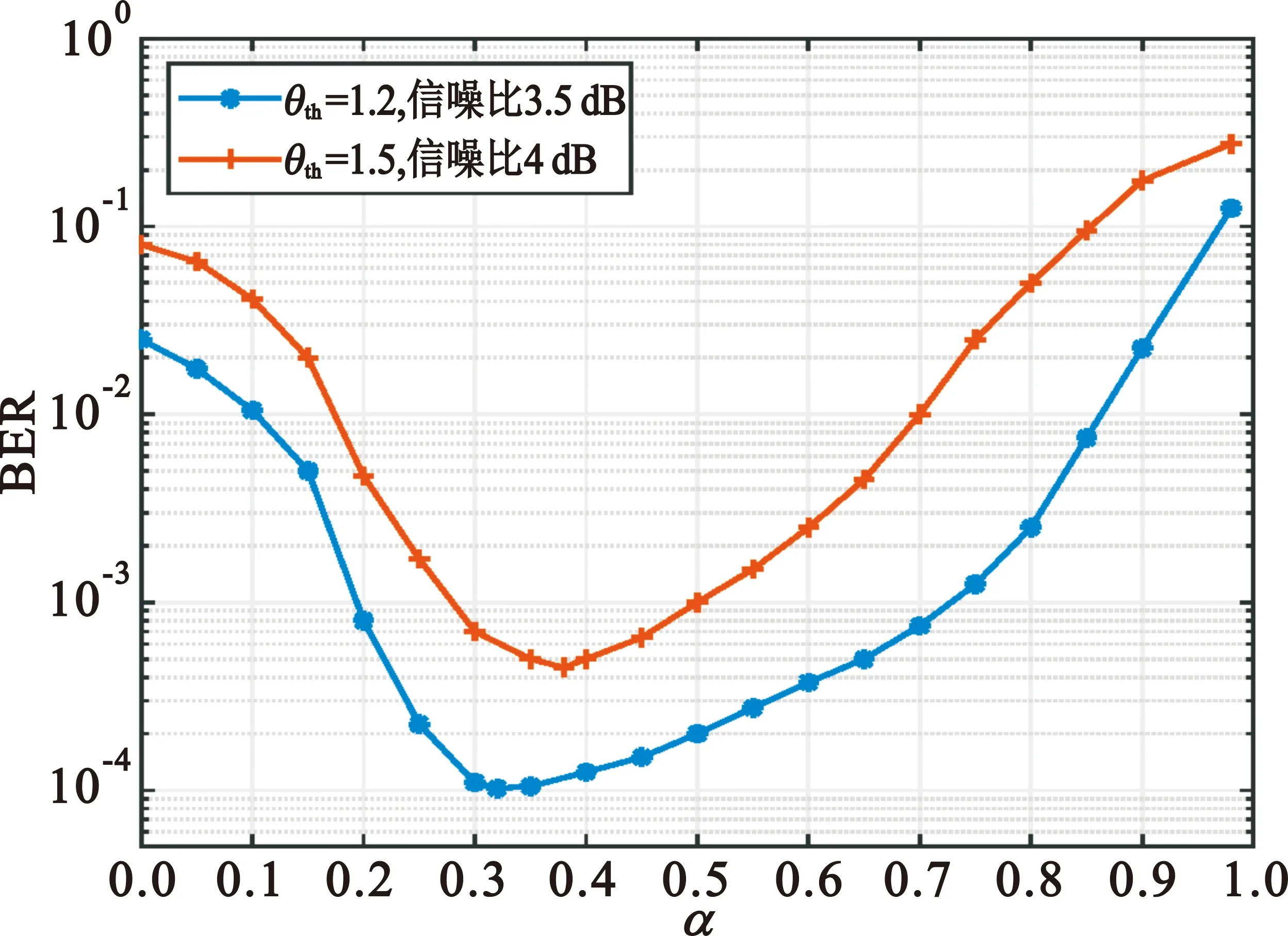
图4 不同信道阈值下BER和α之间的关系

图5给出了不同的SCMA检测算法的误码率性能曲线。此时不同的信道阈值下，不同的算法已经采用最优的α。在之前的分析中可以发现，当θth=0时，混合期望传播算法就是原始的MPA；当θth=∞时，混合期望传播算法就成了期望传播算法(Expectation Propagation Algorithm,EPA)。从图中可以看出，信道阈值越小，系统的误码性能越好。

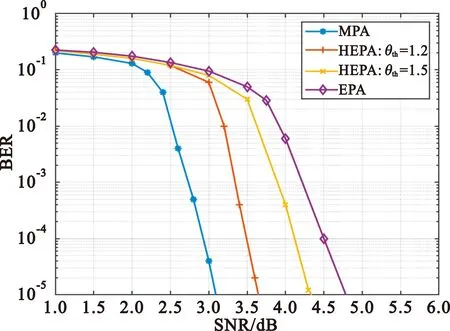
图5 不同SCMA检测算法的BER性能

为了便于比较复杂度，表1给出了不同检测算法需要的乘法次数表达式。结合公式(13)和表1中的表达式，可以建立复杂度和θth之间的关系。 图6给出了以MPA为基准，混合期望传播算法和其他检测算法的复杂度曲线。根据图6，复杂度随着阈值θth增加而降低。因此，结合对于图4的分析可以得出，对于混合期望传播算法，可以使用θth来控制算法的平均复杂度和BER性能。

表1 不同检测算法的复杂度

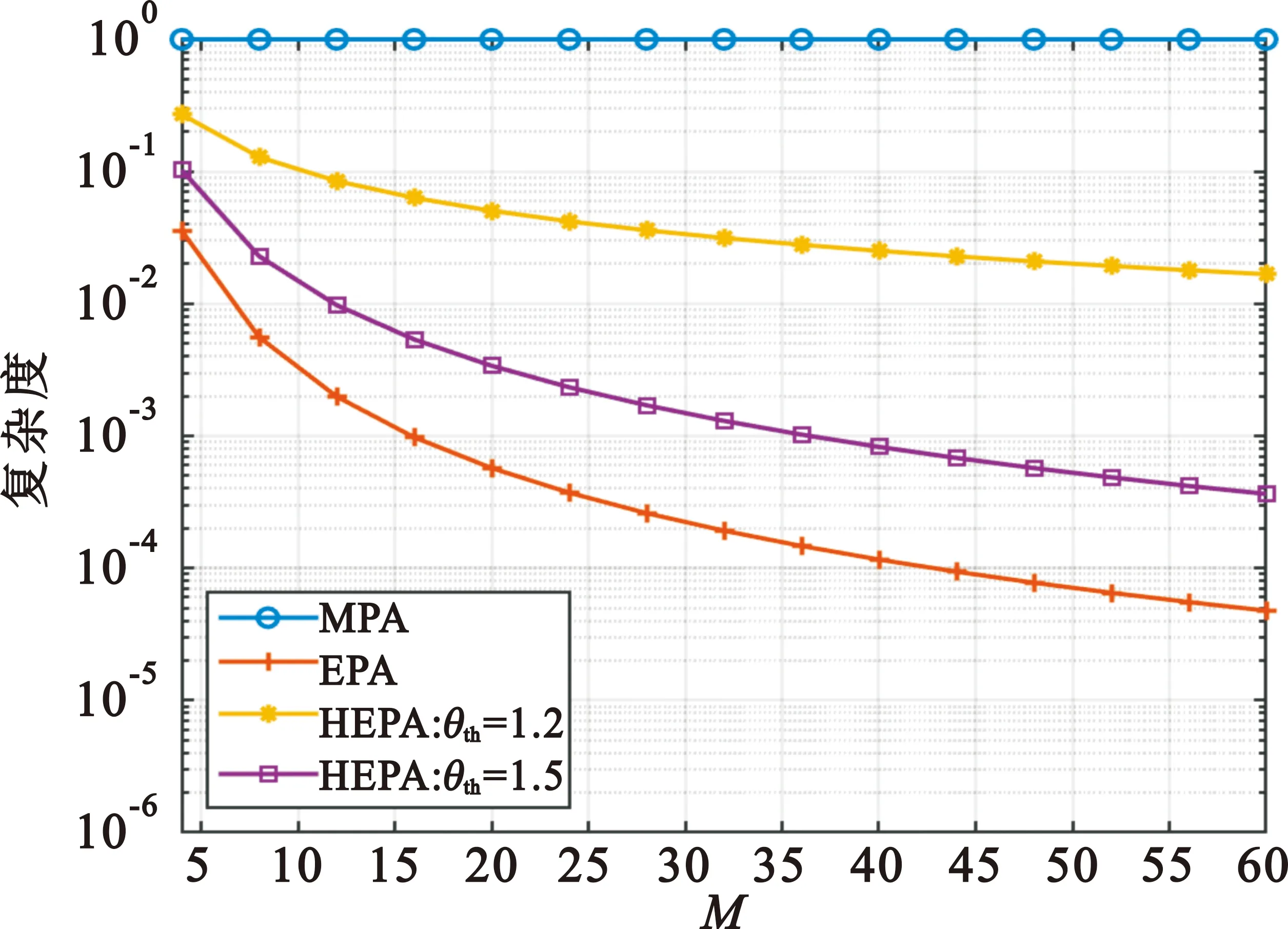
图6 不同SCMA检测算法的复杂度

4 结束语

本文针对SCMA系统提出了一种混合期望传播多用户检测算法，以在算法性能和算法复杂性之间进行折衷。利用信道信息和信道阈值，将因子图上部分信道质量差的边上的概率信息替换为复高斯分布，从而降低了算法复杂度，并建立了算法复杂度与信道阈值的关系。此外，将混合期望传播算法和消息回退机制结合来加快算法收敛和补偿性能损失。仿真结果表明，与其他检测方案相比，提出的混合期望传播算法可以灵活地利用信道信息来实现性能和复杂度之间的平衡。

对于SCMA系统，本文只从接收端研究了复杂度和性能可控的接收机算法。在未来的工作中，将联合考虑接收端的接收机算法和接收端的码本设计，以便降低实现复杂度。