一种基于CMA和DDLMS算法的双模式盲均衡算法*

胡婉如，梅如如，崔 健，王竹刚

(1.中国科学院 国家空间科学中心,北京 100190；2.中国科学院大学,北京 100049；3.北方工业大学 信息学院,北京 100144)

0 引 言

在卫星通信系统中，有限的传输带宽、多径效应和加性噪声等因素会导致接收的码元存在很严重的码间串扰，严重影响通信质量，降低通信的可靠性与稳定性[1]。目前，信道均衡技术是解决这一问题的有效方式，在军事和民用领域都有着广泛的应用前景。由于无线通信信道的传输特性往往是时变的，因此均衡器在处理接收信号时必须实时跟踪信道的变化，才能消除码间串扰，补偿失真的信号。为了实现这一目标，均衡系数可以调整的自适应均衡技术被提出。自适应均衡技术主要分为传统的自适应均衡和盲均衡两类。传统的自适应均衡算法主要有最小均方(Least Mean Square,LMS)算法和递归最小二乘(Recursive Least Squares,RLS)算法两种，需要足够的训练序列才能达到比较好的效果，这会降低频谱利用率[2]，因此本文主要基于盲均衡进行研究。

几十年来，针对不同的应用需求，研究者提出了多种盲均衡算法。其中，最早提出的常模算法(Constant Modulus Algorithm，CMA)易于实现，计算量少，是目前应用最广泛的一种盲均衡算法，但是存在着收敛速度慢、稳态误差大、无法修正相位偏移等缺点[3]。为了进一步改善相位恢复能力[4]，修正恒模算法(Modified Constant Modulus Algorithm，MCMA)被提出，然而其在收敛速度和稳态误差方面并没有明显改进。因此，为了进一步提高均衡器的收敛速度和降低稳态误差，有学者提出了Bussgang类盲均衡算法和判决引导最小均方(Direct Decision Least Mean Square,DDLMS)算法相联合的双模式盲均衡算法。基于该基本原理，王光旭等人[5]提出了基于余弦代价函数的双模盲均衡算法。该算法中两个均衡器并联使用，且使用凸组合结构联合两个均衡器，因此复杂度高。同年，丛文胜[6]提出了并行多模算法(Multimode Algorithm,MMA)+区域多模算法(Regional Multimode Algorithm,RMA)的组合算法。该算法也是两个均衡器并联使用，每一次迭代过程中都需要计算两种算法的误差，因此复杂度也高。此外，该算法在收敛初期利用Bussgang类盲均衡算法使算法的均方误差减小，然后切换到DDLMS算法，使均衡效果达到更优。将Bussgang类盲均衡算法和DDLMS算法结合起来的核心思想是切换或加权，其中切换双模式盲均衡算法通过对每一次的误差进行阈值判断来选择对应的模式。然而该算法只有一个判决阈值，普适性差，容易导致算法不收敛或者收敛非常慢。加权双模式盲均衡算法兼顾两种不同算法误差的误差函数，可以改善算法收敛性能，但是计算复杂度增加。

由以上分析可知，近年来提出的并行双模式算法复杂度高，传统的切换双模式算法和加权双模式算法各有优缺点。因此，为了提高均衡器的收敛性能，降低均衡器的计算复杂度，本文综合切换双模式盲均衡算法和加权双模式盲均衡算法的优缺点，提出一种切换、加权模式联合的CMA+DDLMS双模式盲均衡算法。仿真结果表明，新算法具有更快的收敛速度、更小的剩余误差，以及在不同信噪比情况下都具有更小的误码率。

1 CMA+DDLMS双模式盲均衡算法

由于CMA算法和MCMA算法属于Bussgang类盲均衡算法，它们都具有较大的稳态误差和较慢的收敛速度，因此，CMA和MCMA联合并不会提高均衡性能。此外，MCMA算法只可以纠正具有同相和正交两路信号独立分解特性的调制信号的相偏，无法纠正8PSK、16APSK等调制信号的相偏，且该算法比CMA算法实现复杂。因此，本文基于信号相偏纠正能力、收敛速度和稳态误差等综合考虑，选择CMA和DDLMS相联合的双模式盲均衡算法，其原理图如图1所示。

图1 CMA+DDLMS双模式盲均衡算法原理图

CMA+DDLMS双模式盲均衡算法的工作原理是：首先设置两个判决阈值Rmax和Rmin；当DDLMS算法误差的绝对值|eDDLMS(k)|≥Rmax，选择CMA算法；当|eDDLMS(k)|≤Rmin，选择DDLMS算法；当Rmin≤|eDDLMS(k)|≤Rmax，选择加权双模式盲均衡算法。

CMA+DDLMS双模式盲均衡算法的误差信号为

e(k)=

(1)

式中：μcma、ecma(k)分别是CMA算法的步长因子和误差函数；μDDLMS、eDDLMS(k)分别是DDLMS算法的步长因子和误差函数。

加权函数g(k)的定义为

(2)

式中：γ是常数，用于调节加权函数g(k)。

该加权函数是与DDLMS算法误差有关的非线性函数，|eDDLMS(k)|越接近Rmax，g(k)就越大，此时加权双模式算法误差中CMA误差所占比重更大；|eDDLMS(k)|越接近Rmin，g(k)就越小，此时加权双模式算法误差中DDLMS误差所占比重更大。该加权函数可使得切换模式和加权模式之间的连接更平滑，可有效结合两种模式的优点。

均衡器抽头系数的更新方程为

w(k+1)=w(k)-e*(k)x(k)。

(3)

式中：w(k)为自适应滤波系数向量，x(k)为均衡器输入序列，e*(k)表示为e(k)取复共轭。

CMA算法的步长因子比DDLMS算法的步长因子小两个数量级，CMA+DDLMS双模式盲均衡算法采取固定步长因子，若步长因子选择不当，会对CMA+DDLMS双模式盲均衡算法的收敛造成严重影响，因此，需经过多次仿真找出最佳步长因子。此外，γ、Rmax和Rmin的取值对双模式盲均衡算法的均衡性能和计算复杂度有一定的影响，需要根据不同信道和噪声特性寻找出合适的取值。

2 均衡算法仿真与结果分析

为验证改进算法在卫星通信系统中盲均衡的性能，模拟卫星通信信道对CMA算法、MCMA算法、DDLMS算法和CMA+DDLMS双模式盲均衡算法进行仿真，其具体实现框图如图2所示，CMA+DDLMS双模式盲均衡算法流程图如图3所示。其中仿真采取8PSK调制方式；信道为典型多径信道加高斯白噪声信道，信噪比为25 dB；根升余弦滤波器的滚降系数是0.5，截断的符号范围是8，每个符号输出采样点个数是4；CMA+DDLMS双模式盲均衡算法中CMA算法步长μcma为0.001 9，DDLMS算法步长μDDLMS为0.01，判决阈值Rmax=0.85，Rmin=0.15，加权调节系数γ=9。

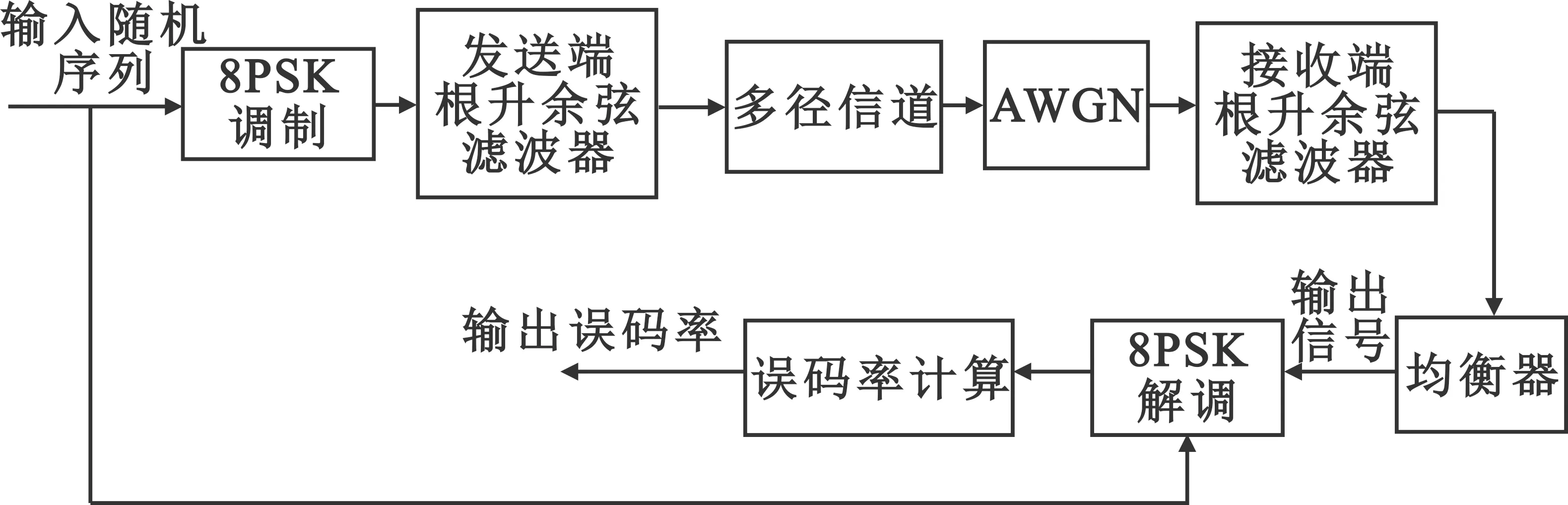
图2 仿真实现框图

图3 CMA+DDLMS双模式盲均衡算法流程图

2.1 不同均衡算法仿真结果

对应无均衡算法和采取不同均衡算法的信号星座图如图4所示，采取不同均衡算法的剩余误差图如图5所示。

图4 信号星座图

(a)CMA

(b)MCMA

(c)DDLMS

(d)CMA+DDLMS图5 不同算法的误差收敛曲线

从图4(a)和图4(b)中可以看出，发射信号在经过卫星通信信道传输后出现了明显的码间干扰，且产生了相位偏移，使得其星座图发散、扭曲，难以判决。从图4(c)～(f)可以看出，经过均衡后的信号星座图较为集中，效果远好于未采取均衡算法的信号。其中，CMA+DDLMS双模式算法均衡后的信号星座图收敛情况最好，DDLMS算法次之，CMA算法和MCMA算法均存在相位偏移。

从图5(a)可知，CMA算法仿真大概2 000个符号后误差趋于稳定，稳态误差值约为0.14；从图5(b)可知，MCMA算法仿真大概3 000个符号后误差趋于稳定，稳态误差值约为0.35；从图5(c)可知，DDLMS算法仿真大概1 000个符号后误差趋于稳定，稳态误差值约为0.06；从图5(d)可知，CMA+DDLMS双模式算法仿真大概600个符号后误差趋于稳定，稳态误差值约为0.1。由此可知，CMA+DDLMS双模式算法收敛速度最快，其稳态误差值只比DDLMS算法略大0.04。

2.2 CMA+DDLMS双模式算法参数性能分析

两个判决阈值Rmax、Rmin和调节系数γ的取值对CMA+DDLMS双模式盲均衡算法的均衡性能和计算复杂度有较大的影响。因此，为研究它们是如何取得最佳值的，给出固定判决阈值Rmax=0.85和Rmin=0.15、只改变调节系数γ时的算法误差收敛曲线，如图6所示，其中图6(c)与图5(d)为相同情况下的仿真。此外，固定调节系数γ=9，只改变判决阈值Rmax和Rmin时的算法误差收敛曲线如图7所示。

从图6(a)可知，γ=1时，CMA+DDLMS双模式盲均衡算法不收敛;从图6(b)可知，γ=5时，CMA+DDLMS双模式算法仿真大概1 500个符号后误差趋于稳定，稳态误差值约为0.2，收敛速度较慢，稳态误差值大；从图6(c)可知，γ=9时，CMA+DDLMS双模式算法仿真大概600个符号后误差趋于稳定，稳态误差值约为0.1，收敛速度快，稳态误差值小；从图6(d)可知，γ=15时，CMA+DDLMS双模式盲均衡算法仿真大概600个符号后误差趋于稳定，稳态误差值约为0.1，收敛性能与γ=9时相近。因此可知，γ值过小，会导致不收敛或稳态误差过大；γ值过大，性能无明显提升，且会增加计算复杂度。因此，基于均衡性能和计算复杂度考虑，选取γ=9。

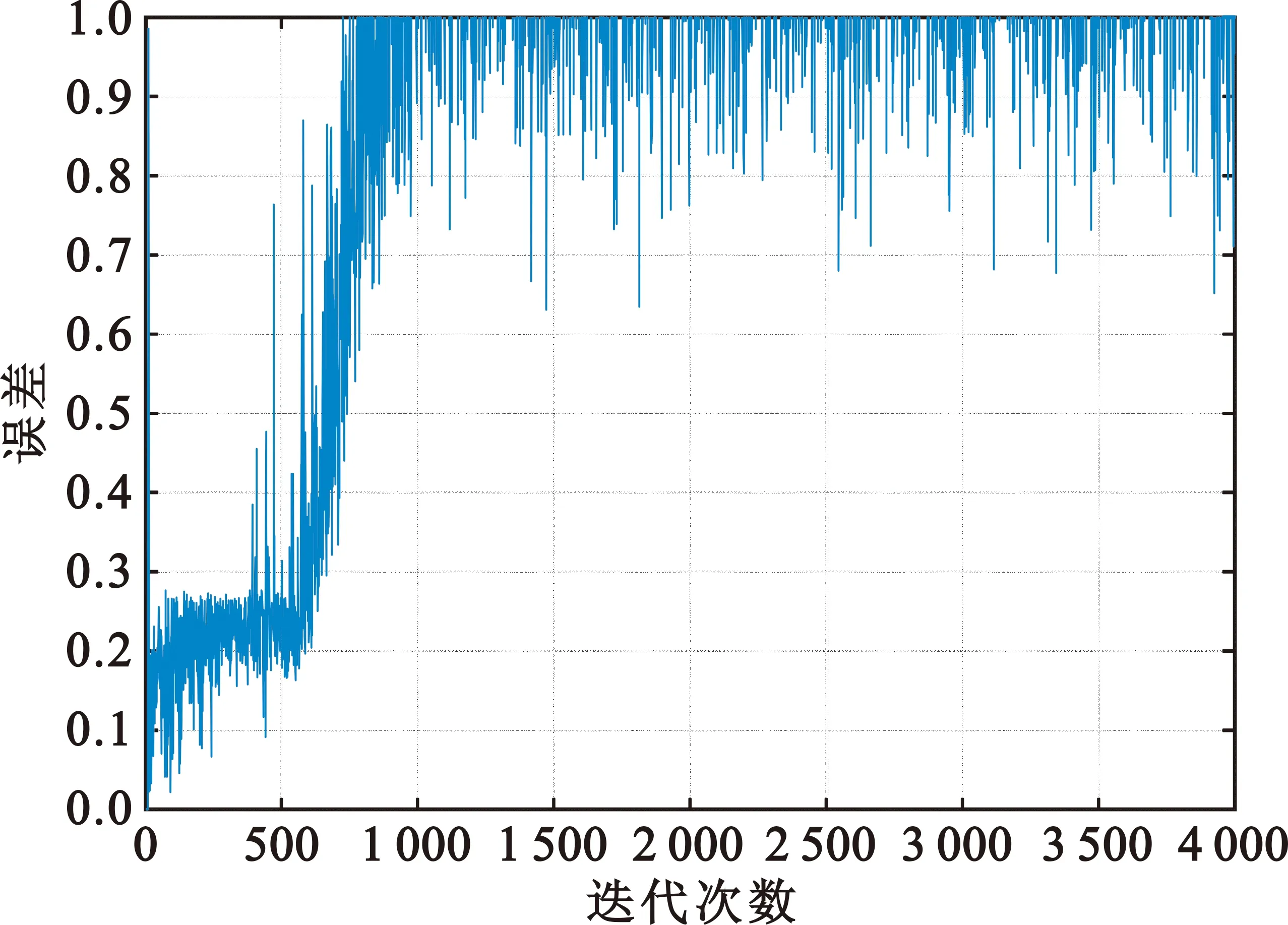
(a)γ=1

(b)γ=5

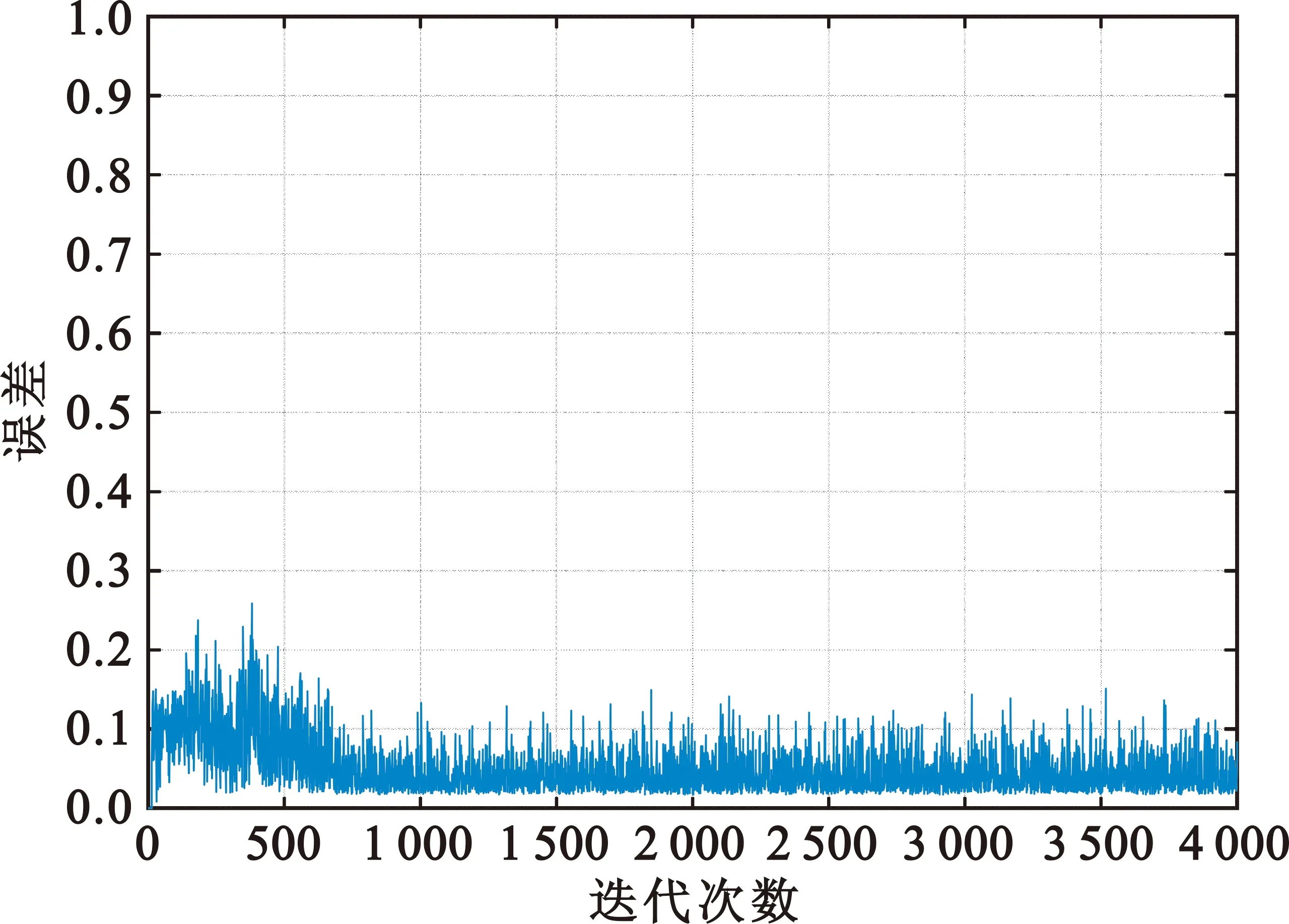
(c)γ=9

(d)γ=15图6 不同调节系数γ时CMA+DDLMS算法误差收敛曲线

(a)Rmax=0.6，Rmin=0.4

(b)Rmax=0.7，Rmin=0.3

(c)Rmax=0.8，Rmin=0.2

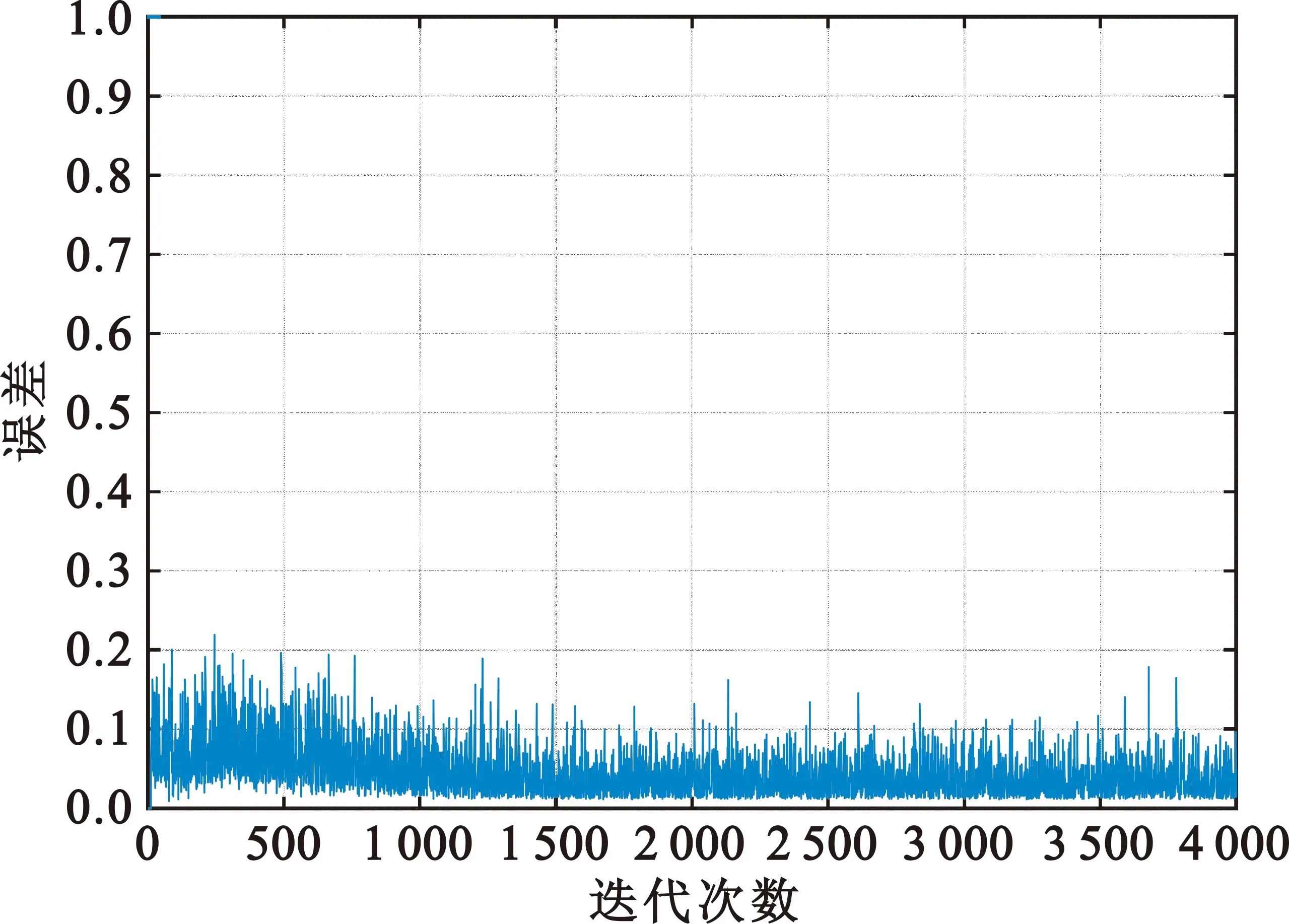
(d)Rmax=1，Rmin=0图7 不同判断阈值下CMA+DDLMS算法误差收敛曲线

从图7(a)可知，Rmax=0.6、Rmin=0.4时，CMA+DDLMS双模式算法无法收敛；从图7(b)可知，Rmax=0.7、Rmin=0.3时，CMA+DDLMS双模式算法仿真大概1 300个符号后误差趋于稳定，稳态误差值约为0.2，收敛速度较慢，稳态误差值大；从图7(c)可知，Rmax=0.8、Rmin=0.2时，CMA+DDLMS双模式算法仿真大概1 200个符号后误差趋于稳定，稳态误差值约为0.13，收敛速度较快，稳态误差值较小；从图6(c)可知，Rmax=0.85、Rmin=0.15时，CMA+DDLMS双模式算法仿真大概600个符号后误差趋于稳定，稳态误差值约为0.1，收敛速度快，稳态误差值小。从图7(d)可知，Rmax=1、Rmin=0时，CMA+DDLMS双模式算法仿真大概1 500个符号后误差趋于稳定，稳态误差值约为0.1，收敛性能与Rmax=0.85、Rmin=0.15时相近，然而此时由于Rmax过大、Rmin过小，会一直处于加权模式，计算复杂度增大。因此可知，Rmax过小、Rmin过大，会导致不收敛或稳态误差过大；Rmax过大、Rmin过小，性能无明显提升，且会增加计算复杂度。因此，基于均衡性能和计算复杂度考虑，选取Rmax=0.85，Rmin=0.15。

由以上分析可知，本文最终确定该算法中Rmax=0.85，Rmin=0.15，γ=9。此外，从图6(c)中可知，在Rmax=0.85、Rmin=0.15、γ=9的情况下，CMA+DDLMS双模式算法在仿真600符号后误差即降低至0.15以下，说明该算法的仿真主要是在DDLMS算法模式，加权模式持续时间很短。此外，由于DDLMS算法复杂度较低，因此，计算复杂度并未有较大增加。

2.3 不同均衡算法误码率性能对比

按照图2，基于前面的仿真条件，即CMA+DDLMS双模式盲均衡算法的判决阈值Rmax=0.85，Rmin=0.15，加权调节系数γ=9，在不同信噪条件下，对无均衡、CMA算法、MCMA算法、DDLMS算法和CMA+DDLMS双模式盲均衡算法进行仿真，得到无均衡以及不同均衡算法的误码率曲线如图8所示。

图8 四种算法误码率曲线对比

由图8可知，加均衡算法误码率性能优于无均衡算法误码率性能，且在不同信噪比条件下，CMA+DDLMS双模式盲均衡算法误码率性能优于DDLMS算法误码率性能，DDLMS算法误码率性能优于CMA算法误码率性能，CMA算法误码率性能优于MCMA算法误码率性能。其中，在25 dB信噪比时CMA+DDLMS双模式盲均衡算法误码率约为10-6，优于DDLMS算法，且在信噪比大于13 dB时，CMA+DDLMS双模式盲均衡算法误码率均小于10-5。因此，CMA+DDLMS双模式盲均衡算法在低信噪比条件和高信噪比条件下性能都是最优的。

3 结束语

本文提出了一种切换模式和加权模式联合的CMA+DDLMS双模式盲均衡算法。该算法综合了CMA+DDLMS切换双模式算法和CMA+DDLMS加权双模式算法的优点，提高了切换双模式均衡算法的收敛性能，改善了加权双模式均衡算法计算复杂度高等问题。基于8PSK调制解调平台模拟卫星通信信道，对不同均衡算法进行仿真，结果表明，相比于CMA算法和MCMA算法，CMA+DDLMS双模式算法收敛速度更快，稳态误差更小，且具有纠正相位偏移的能力；相比于DDLMS算法，CMA+DDLMS双模式算法收敛速度更快。在不同信噪比条件下，CMA+DDLMS双模式算法相比于CMA算法、MCMA算法和DDLMS算法，误码率更小。接下来将对该算法的实现复杂度做进一步的优化。