优化参数对CPM-PSWF信号性能的影响*
杨大伟,刘传辉,康家方,刘锡国
(1.海军航空大学 航空通信教研室,山东 烟台 264001;2.中国人民解放军91439部队,辽宁 大连 116041)
0 引 言
连续相位调制(Continuous Phase Modulation,CPM)属于数字相位调制技术,是1981年由Anderson和Aulin等人[1-2]在连续相位频移键控(Continuous Phase Frequency Shift Keying,CPFSK)、最小频移键控(Minimum Shift Keying,MSK)、正弦频移键控(Sinusoidal Frequency Shift Keying,SFSK)、高斯最小频移键控(Gaussian Minimum Shift Keying,GMSK)等调制方式基础上系统阐述的一类调制方法。CPM信号不仅具有很高的频带利用率和功率效率,还可以很好地抵御非线性影响,在移动通信、深空探测、遥感通信、卫星通信等领域应用广泛[3-5]。现有的CPM基带调频脉冲信号主要有矩形脉冲信号、升余弦脉冲信号、类高斯脉冲信号等,不同的基带脉冲信号决定了CPM调制信号不同的频谱性能[6]。
椭圆球面波函数(Prolate Spheroidal Wave Function,PSWF)是Bell实验室Slepian等人[7-8]于1961年定义的一类特殊函数集合,具有高时频能量聚集性、时间带宽积灵活可控性、完备正交性等优良基础特性,在雷达、卫星通信、光学、超宽带通信等领域都有所应用。相同参数条件下,0阶PSWF信号又是PSWF信号集中最佳时频能量聚集性信号[9]。目前,对CPM技术研究的相关文献大多以CPM相关联技术及其改进算法为主,从基带波形信号设计方面对CPM进行研究的相关文献并不多,那么相对于CPM常用基带调频脉冲信号,如果将具有优良基础特性的PSWF信号作为CPM基带信号,引入CPM调制,有望进一步提高现有CPM调制信号的能量聚集性和频带利用率。
本文将PSWF信号作为CPM的基带调频脉冲信号,结合CPM原理,提出了基于椭圆球面波信号的连续相位调制(CPM Based on PSWF,CPM-PSWF)方法,给出了CPM-PSWF调制信号产生原理。另一方面,由于PSWF的时间带宽积、阶数、调制指数、关联长度等调制参数又进一步影响着CPM-PSWF调制信号的功率谱密度、信号占用带宽等性能,所以,研究不同参数变化对CPM-PSWF调制信号性能影响,为CPM-PSWF信号在不同场景应用中的参数选择提供参考依据,同时这也对提高CPM调制信号性能具有重要的借鉴意义。
1 CPM-PSWF信号描述
CPM-PSWF调制信号产生原理框图如图1所示。首先,将PSWF信号作为CPM基带调频脉冲信号即ψ(c,t),对ψ(c,t)积分并波形归一化处理后,得到相位成形脉冲函数q(t);其次,计算q(t)与调制指数等参数的乘积,将信息符号序列ai加载到相位信息上,得到载波时变相位φ(t,a);最后,将φ(t,a)经过载波调制变为带通信号,得到相位连续且包络恒定的CPM-PSWF调制信号s(t)。

图1 CPM-PSWF信号调制原理框图
CPM-PSWF调制信号s(t)表达式为
(1)
式中:E为码元符号信号能量;T为码元时间间隔;ωc为载波角频率,且ωc=2πfc,fc为载波中心频率;φ0为载波初始相位;φ(t,a)为载波的时变相位,也是信息承载项,其数学表达式为
(2)
式中:h为调制指数;ai为发送的码元信息符号序列,单个码元有M种取值,分别为±1,±3,…,±(M-1),i=0,±1,±2,…;q(t)为CPM信号相位成形脉冲函数,其表达式为
(3)
式中:ψ(c,t)表示椭圆球面波信号,其积分方程表达式为
(4)
式中:ψ(c,t)是带限于[-Ω,Ω]又在时域区间[0,LT]上集中分布的椭圆球面波函数,c=LTΩ是其时间带宽积;λ是对应于ψ(c,t)的特征值;L为信号关联长度,L=1为全响应CPM-PSWF信号,L>1为部分响应CPM-PSWF信号。
符号能量E和比特能量Eb的关系如下:
E=EblbM。
(5)
同符号能量和比特能量关系,类似的符号周期T与比特周期Tb关系如下:
T=TblbM。
(6)
由以上CPM-PSWF调制信号产生表达式可知,CPM-PSWF信号的频谱性能与发送信息进制数M、信息传输速率R(1/T)、调制指数h、关联长度L、时间带宽积c等参数有关,分析这些参数对CPM-PSWF调制信号性能的影响,可以为CPM-PSWF信号将来在不同场景应用,选择满足条件的调制参数提供参考依据。
2 CPM-PSWF谱密度计算
根据维纳辛钦定理,随机信号的自相关函数和功率谱密度(Power Spectral Density,PSD)是傅里叶变换对,通常可以通过对自相关函数求傅里叶变换得到随机信号的功率谱密度,采用最易实现的数值计算方法计算CPM-PSWF调制信号功率谱密度,步骤如下:
Step1 计算CPM-PSWF调制信号等效低通信号的自相关函数R(τ):
R(τ)=R(τ′+mT)

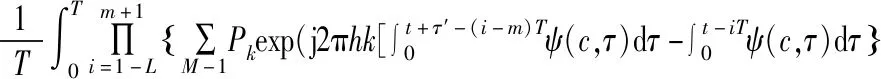
(7)
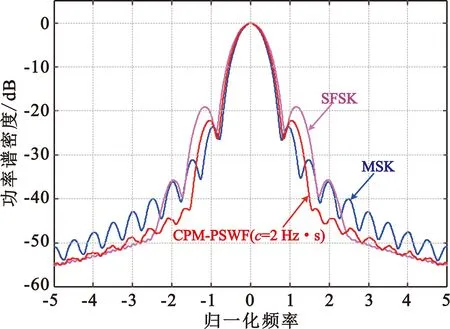
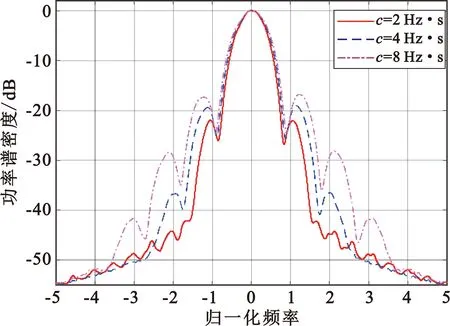
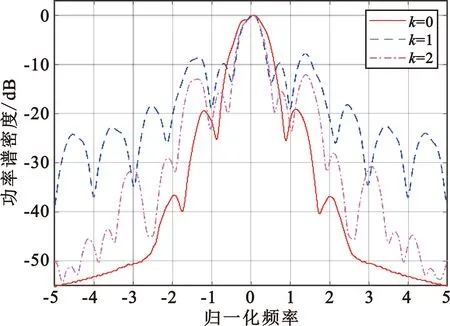
式中:τ=τ′+mT,0≤τ′ Step2 计算常数Cα: (8) Step3 计算CPM-PSWF信号的功率谱密度: (9) 式中:第一项是τ在0~LT范围内R(τ)的傅里叶变换,第二项是τ在LT~(L+1)T范围内R(τ)的傅里叶变换。 由于椭圆球面波函数没有闭式解析解,而且像MSK、SFSK、GMSK等调制信号的自相关函数、功率谱密度计算过程往往也十分复杂,所以需要在理论分析的基础上结合计算机数值仿真来验证CPM-PSWF调制信号的频谱性能。为了更加清晰直观地分析不同参数对CPM-PSWF调制信号功率谱密度的影响,本文采用韦尔奇(Welch)谱密度估计法对调制信号的功率谱密度进行估计。 由CPM-PSWF信号表达式可知,其调制信号功率谱密度特性取决于PSWF信号的时间带宽积c、PSWF信号阶数、调制指数h、关联长度L、码元速率R、进制数M等参数,当这些参数变化时,调制信号带宽及其频谱带外衰减也会随之发生变化。本节在Matlab2016a仿真环境下,通过数值计算的方法,在给定相同参数条件下,改变CPM-PSWF信号某一调制参数值(如在PSWF信号阶数、调制指数h、关联长度L、码元速率R、进制数M等参数都相同条件下,只改变PSWF的时间带宽积c),分析其对CPM-PSWF信号的影响。按照该方法,依次改变PSWF信号阶数、调制指数h、关联长度L、码元速率R、进制数M,分别分析每个参数对CPM-PSWF调制信号频谱特性的影响。由于带通信号的功率谱密度是其等效低通信号的时移形式,因此采用基带信号处理方式,利用Welch功率谱密度估计后,可以进一步通过数字积分得到带外功率占比与调制信号占用带宽之间的关系,其中,PSWF信号由DPSS[10]方式产生。具体参数设置如表1所示。 表1 仿真参数 图2是CPM-PSWF信号与MSK、SFSK调制信号的功率谱特性对比图,MSK是基带调频脉冲为矩形脉冲的CPM调制方式,SFSK是基带调频脉冲为升余弦脉冲的CPM调制方式。相同调制参数条件下,由图2可知,当PSWF信号的时间带宽积为2 Hz·s时,CPM-PSWF信号的功率谱密度带外衰减更快。 图2 CPM-PSWF与MSK、SFSK信号的PSD 表2是不同调制方式在不同功率百分比情况下占用的归一化带宽值。由表2可知,CPM-PSWF信号与MSK、SFSK调制信号相比,在包含信号99.9%功率带宽条件下,可分别提升系统频带利用率约13%(即(2.84-2.47)/2.84)和16%(即(2.94-2.47)/2.94)。 表2 给定功率百分比不同调制方式占用带宽 图3是部分响应条件下,关联长度L为3时,CPM-PSWF信号与GMSK调制信号的功率谱密度。当高斯脉冲的时间带宽积BT典型值为0.3(GSM信号参数)、0.5时的GMSK调制信号,分别与PSWF时间带宽积为2 Hz·s、4 Hz·s的CPM-PSWF调制信号相比,CPM-PSWF信号功率谱的高频滚降和带外衰减较快,而且功率谱主瓣带宽也均小于GMSK。 图3 CPM-PSWF与GMSK信号PSD 由表3可知,在部分响应条件下,通过设置PSWF的时间带宽积参数,在相同功率百分比条件下,CPM-PSWF调制信号占用带宽也可以小于典型值GMSK信号。尤其是当PSWF的时间带宽积c为2 Hz·s时,CPM-PSWF调制信号频谱性能(带外衰减、高频滚降、占用带宽)相对较好。 表3 给定功率百分比不同调制方式占用带宽(L=3) 下面分析算法复杂度。如表1所示,单个码元周期内信号采样点数为N,信号持续时间为nT,假定余弦函数的计算量为4倍乘法运算量,正弦基(sinc)函数的计算量为6倍乘法运算量,而正态分布函数Q(·)涉及指数幂的积分运算,为了便于比较,将Q(·)的计算量等价为10次乘法与10次加法运算量,产生一个N行N列矩阵,相当于N2的运算量。那么,结合矩形脉冲、升余弦脉冲、(类)高斯脉冲和PSWF信号的产生、积分、归一化处理、信息加载、载波相位调制等过程,分别得到MSK、SFSK、GMSK、CPM-PSWF信号产生的算法复杂度。 以CPM-PSWF信号产生过程为例,首先,对PSWF信号的带宽与时间乘积求sinc函数值,该步骤乘法运算量为O(6N);然后,生成sinc函数值的托普利兹矩阵,并计算其特征值,取其中第1列数据获得0阶PSWF信号,乘法运算量为N×N近似为O(N2);其次,对PSWF信号积分(乘法运算量为O(1)、加法运算量为O(N))、归一化处理(乘法运算量为O(2N))、信息加载(乘法运算量为O(nN))、载波相位调制(乘法运算量为O(4nN)),所以CPM-PSWF信号产生的乘法运算复杂度为O(6N+N2+1+2N+nN+4nN),合并并保留高阶项得O(N2+5nN),其加法运算复杂度为O(N)。MSK、SFSK、GMSK等CPM调制信号产生过程,只是基带信号不同,因此与CPM-PSWF信号产生运算复杂度计算过程相似,可以得到其他调制信号的算法复杂度。因为不同调制信号加法复杂度运算量基本相当,而乘法运算复杂度要远高于加法运算,故以乘法运算复杂度为度量标准。不同调制方式信号产生算法复杂度如表4所示。 表4 不同调制信号产生算法复杂度 由表4可知,调制信号产生算法复杂度由低到高依次为MSK、SFSK、GMSK、CPM-PSWF,CPM-PSWF信号的运算复杂度主要在于PSWF信号的数值产生过程。虽然CPM-PSWF信号产生复杂度相对较高,但是,一方面利用PSWF信号的高时频能量聚集性、时间带宽积灵活可控性可以获得频带利用率较高的CPM信号,另一方面现代数字电路技术的发展程度也有利于快速实现PSWF信号的产生。 PSWF的时间带宽积c作为其CPM-PSWF信号的重要参数,通过影响CPM基带调频信号ψ(c,t)从而影响着CPM-PSWF调制信号的频谱性能。选取CPM-PSWF调制信号参数为进制数M=2,调制指数h=0.5,PSWF信号的关联长度L=1(全响应),比特传输速率为50 b/s,仿真得到的功率谱密度及相对带外功率归一化带宽占比关系如图4所示。 (a)功率谱密度 (b)功率百分数占用带宽图4 不同时间带宽积CPM-PSWF信号PSD与功率百分数占用带宽 由图4可知,当PSWF的时间带宽积分别为2 Hz·s、4 Hz·s、8 Hz·s时,CPM-PSWF调制信号的归一化双边带宽(占总功率99.9%信号带宽)分别为2.43、2.87、4.28。随着PSWF的时间带宽积变大,CPM-PSWF调制信号的占用带宽也随着增大,也就是说改变时间带宽积会影响调制信号带宽。PSWF的时间带宽积越小,调制信号功率谱密度特性第一旁瓣越低,带外衰减越快。 图5给出了不同时间带宽积条件下CPM-PSWF调制信号在给定功率百分比(90%、99%、99.9%)下占用带宽曲线。随着PSWF时间带宽积c的增加,CPM-PSWF调制信号在相同功率占比情况下,占用带宽越宽;时间带宽积c越小,占用带宽越小;随着PSWF时间带宽积c增大,CPM-PSWF调制信号的频谱旁瓣衰减减慢,-40 dB以上高频滚降越慢。所以,PSWF时间带宽积越小,CPM-PSWF信号频谱性能越好。这些特性也与PSWF信号的基础特性相关,且与PSWF信号在时宽一定时,随着时间带宽积增大,相应的调制信号带宽增加是一致的。 图5 时间带宽积与CPM-PSWF信号功率占用带宽关系 在相同时间带宽积、同一频段下,可以产生多阶PSWF信号,这是PSWF与矩形脉冲、升余弦脉冲、高斯脉冲相比所具有的独特性质。下面分析对比不同阶PSWF信号对CPM-PSWF调制信号频谱性能的影响。 图6和图7是当PSWF信号的时间带宽积分别为2 Hz·s、4 Hz·s时产生的0阶PSWF信号、1阶PSWF信号、2阶PSWF信号,分别作为CPM基带调频脉冲得到的CPM-PSWF功率谱密度和不同带宽条件下占用的功率百分数。由图可知,基于0阶PSWF信号得到的调制信号频谱,不论是占用带宽还是带外衰减、频谱滚将性能都要优于1阶PSWF和2阶PSWF,且基于2阶PSWF的CPM调制信号频谱带外衰减速度要比1阶PSWF快,且随着时间带宽积的增加,基于2阶PSWF的CPM频谱性能要更快速接近于0阶PSWF,这与偶数阶PSWF信号波形偶对称、其积分信号对CPM相位路径影响有关。当PSWF时间带宽积为2 Hz·s时,占总功率90%的信号功率归一化双边带宽分别为0.84(0阶)、2.92(1阶)、2.74(2阶),且在带宽大于2.50时,基于2阶PSWF的CPM调制信号在相同带宽条件下,其功率百分数越高;当PSWF时间带宽积为4 Hz·s时,占总功率90%的信号功率归一化双边带宽分别为0.92(0阶)、3.14(1阶)、1.56(2阶),随着时间带宽积的增大,PSWF的1阶、2阶信号能量聚集度变高,基于2阶PSWF的CPM调制信号占用带宽也相对越小。 (a)功率谱密度 (b)功率百分数带宽图6 c=2 Hz·s不同阶数CPM-PSWF信号PSD与功率百分数占用带宽 (a)功率谱密度 (b)功率百分数带宽图7 c=4 Hz·s不同阶数CPM-PSWF信号PSD与功率百分数占用带宽 由以上分析可知,0阶PSWF是相同条件下一组PSWF中时频能量聚集性最佳信号,同样适用于CPM调制信号中,虽然随着PSWF阶数的增加,PSWF信号本身能量聚集性也会随之有所下降,但是偶数阶PSWF信号要比奇数阶PSWF更适合作为CPM基带调频脉冲信号,这也与PSWF信号不同阶信号产生求解方法本身有关。 调制指数h是影响CPM调制信号频谱性能的重要参数,通常分为恒定指数和多指数两种,而多指数h条件下的CPM信号分析复杂。这里以恒定指数作为分析基础条件,对CPM-PSWF调制信号性能影响进行分析。选取CPM-PSWF调制信号参数为进制数M=2,PSWF信号的时间带宽积c=2 Hz·s,信号的关联长度L=1(全响应),传输符号速率为50 b/s,仿真得到的功率谱密度及相对带外功率归一化带宽占比关系如图8所示。 (a)功率谱密度 (b)功率百分数带宽图8 不同调制指数CPM-PSWF信号PSD与功率百分数占用带宽 由图8可知,调制指数h分别为0.5、0.6、0.7时,CPM-PSWF调制信号的含99.9%的功率归一化带宽分别为2.43、2.64、2.81。随着调制指数h的增大,CPM-PSWF调制信号占用带宽也随之增大;h越小,信号占用带宽越窄,带宽利用率越高,调制信号功率谱密度第一旁瓣越低,但当h减小时会影响接收端的解调性能。 关联长度L的选择主要存在CPM部分响应情况(L>1)时,不同关联长度对CPM-PSWF调制信号的功率谱带外衰减和带宽会产生影响。选取CPM-PSWF调制信号参数为进制数M=2,PSWF信号的时间带宽积c=2 Hz·s,调制指数h=0.5,比特传输速率为50 b/s,仿真得到的功率谱密度及相对带外功率归一化带宽占比关系如图9所示。 (a)功率谱密度 (b)功率百分数带宽图9 不同关联长度CPM-PSWF信号PSD与功率百分数占用带宽 由图9可知,当基带调频PSWF信号关联长度分别选为L=1(全响应)、L=3(部分响应)、L=5(部分响应)时,CPM-PSWF调制信号占99.9%功率归一化带宽大小分别为2.43、1.16、0.94。随着关联长度L的增大,“相关编码”效果越明显,CPM-PSWF调制信号频谱主瓣宽度越小,带外辐射更小。可以增大关联长度L来减小信号占用带宽,但是L的增大一方面会用信噪比作为代价来换取较好的频谱特性,另一方面也会增加接收端解调的复杂度。 选取CPM-PSWF信号的调制参数为PSWF的时间带宽积c=2 Hz·s,调制指数h=0.5,基带调频脉冲PSWF信号关联长度L=1(全响应条件),比特传输速率为50 b/s,分别取进制数M为2、4、8,数值计算得到功率谱密度和不同功率百分数占用归一化带宽曲线如图10所示。 (a)功率谱密度 (b)功率百分数带宽图10 不同进制数CPM-PSWF信号PSD与功率百分数占用带宽 由图10可知,当选取进制数M分别为2、4、8时,CPM-PSWF调制信号的占总功率99.9%功率归一化双边带宽分别为2.43、3.82、6.86。随着进制数M的增大,功率谱密度的带外辐射减小,但是占用带宽增加。对带外功率抑制要求较高时,可以考虑增加进制数,但是M的增大会增加接收端检测的复杂度。 选取CPM-PSWF信号的调制参数为PSWF的时间带宽积c=2 Hz·s,调制指数h=0.5,基带调频脉冲PSWF信号关联长度L=1(全响应条件),比特传输速率为8 kb/s、16 kb/s、32 kb/s,进制数M=2,数值计算得到功率谱密度和不同功率百分数占用带宽如图11所示。 (a)功率谱密度 (b)功率百分数带宽图11 不同码元速率CPM-PSWF信号PSD与功率百分数占用带宽 由图11可知,当码元传输速率分别为8 kb/s、16 kb/s、32 kb/s时,CPM-PSWF调制信号占总功率99.9%双边带宽分别为19.92 kHz、39.84 kHz、79.64 kHz。从数值分析可得,码元速率以相应倍数增加,其调制信号带宽近乎以相同倍数增加,但其功率谱密度呈现带外衰减减慢的趋势。也就是说,码元速率的改变会影响CPM-PSWF调制信号占用带宽大小,但对系统频带利用率不产生影响。 综上所述,不同参数对CPM-PSWF调制信号频谱的性能影响不同,当数据传输速率一定时,选用0阶PSWF作为CPM-PSWF信号的基带调频脉冲,通过减小PSWF的时间带宽积c、调制指数h、进制数M,增加关联长度L,可以获得更好的CPM-PSWF调制信号频谱性能和频带利用率。PSWF的时间带宽积c越小,CPM-PSWF信号功率谱密度带外衰减越快;调制指数h越小,关联长度L越大,CPM-PSWF信号占用带宽越小;进制数M越小,CPM-PSWF信号的复杂度就越低。但是调制指数h的减小会影响CPM-PSWF系统接收端的解调性能,而且随着关联长度L的变大,会增加接收端解调的复杂度。所以,PSWF信号在实际工程应用中,应根据不同场景应用需求和指标综合考量、选择调制参数。 本文给出了一种基于椭圆球面波信号的连续相位调制方法,分析了优化调制参数对CPM-PSWF调制信号性能的影响。在相同参数条件下,以具有最佳时频能量聚集性的0阶PSWF作为CPM-PSWF的基带调频脉冲,调制信号频谱带外衰减快,占用带宽小;PSWF的时间带宽积和调制指数越小、关联长度越长,调制信号频谱性能越好,这也为下一步研究基于PSWF的最优CPM调制解调方法提供了参考依据。在选取最优参数时,还应兼顾系统带宽、功率谱和系统误码性能、调制解调实现复杂度等因素权衡考虑,以满足实际不同应用场景需求,为CPM-PSWF信号推向实际应用提供参考。


3 实验结果与分析

3.1 CPM-PSWF调制信号性能




3.2 PSWF时间带宽积


3.3 PSWF阶数



3.4 调制指数


3.5 关联长度


3.6 进制数


3.7 码元速率


4 结束语

