流激振动对弧形闸门启闭力的影响

刘 朋，徐国宾，杨佼佼

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300354；2.中国电建集团 贵阳勘测设计研究院有限公司，贵阳 550081)

1 研究背景

随着高库大坝的建设和金属制造工艺的提升，水工建筑物不断向高水头大流量的趋势发展。闸门作为水工建筑物中必不可少的一部分，启闭问题将决定整个水利枢纽能否正常发挥应有的功能。现有的水工闸门启闭力的计算方法主要依赖于经验公式，对诸多工程因素并未进行详细的考虑。随着研究的深入和工程实践经验的积累，人们逐渐意识到流激振动对闸门面板受力以及支承、止水摩擦力的影响也是决定闸门启闭力的一个重要因素。因此如何科学合理地计算流激振动引起的闸门启闭力的变化对启闭机容量的选择非常重要。

我国现行的《水利水电工程钢闸门设计规范》(SL 74—2013)[1]虽然给出了闸门启闭力的计算方法，但对许多因素却未作详细阐述。目前国内外学者对此开展了大量研究，取得了一些成果。徐国宾等[2]通过分析大量实测资料，发现大部分闸门底孔前的泥沙淤积体为宾汉体，在此基础上给出了在泥沙淤积的情况下闸门启门力的计算方法；Menon和Mudgal[3]通过模型验证，分析了闸门底缘形式对闸下流态和闸门受力的影响；张冬等[4]在考虑了门顶水压力、垂直水动力的基础上利用数值模拟的方法对闸门启闭力时程变化做了进一步分析。虽然在此基础上，启闭力的计算精度得到了提高，但以上研究也都未考虑流激振动，对于振动严重的闸门，计算结果存在一定误差。而且目前关于闸门流激振动的研究大都停留在结构方面：Ren等[5]结合物理模型试验和数值模拟，采用随机振动原理分析了水下卧倒闸门流激振动特性；严根华[6]根据不同的大跨度闸门的流激振动特性，分别给出了相应的振动控制方案；Anami等[7]利用模型试验分析了启闭过程中闸门振动对弧形闸门转动轴以及侧止水摩擦的影响，证明了从摩擦维持稳定性到完全不稳定性和闸门失效的突然转变。这些研究都着力于流激振动对结构稳定性的影响，并未考虑改变闸门面板受力而造成的启闭摩擦力的变化，以及在强振动的情况下出现的启闭力增大[8-9]的情况，因此有必要在闸门启闭力计算公式中将流激振动诱发的激振力考虑进去，以提高闸门启闭力的计算精度。

本文从理论推导和实际工程对比两方面出发，提出在动水中弧形闸门面板受力以及启闭力的计算方法,分析不同闸门开度下诱发的激振力对闸门启闭力的影响，用于指导启闭机容量的选择。

2 理论推导

弧形闸门的挡水面可视为弧形加肋圆柱壳中的一部分[10]，主要产生径向、法向和侧向位移，作用于弧形闸门的径向水压力通过弧形闸门面板经支臂传递到闸门的转动支铰处。当振动严重时，会造成闸门支臂的变形，甚至破坏[11-13]，振动较小时，也将引起支铰与转轴之间的挤压，改变摩擦力臂，增大摩擦系数，进而导致闸门开启或关闭时的摩擦力增大。下面将以数值模拟结果进一步分析说明。

2.1 作用机理

本文选取玛尔挡水电站泄洪放空洞工作闸门作为研究对象，基于ANSYS的workbench模块进行流固耦合模拟计算，并监测闸门受到的水压力和闸门振动位移。对于闸门附近的结构和流体采用非结构化网格，能更好地适应边界变形。水库进口通过UDF(用户自定义函数)将其设置为静水压强压力分布入口，库区入口和事故闸门门井顶部为空气入口，下游为无压出流。闸门和水体的交界面承担着数据传输的作用，设置为流固耦合面，模型采用VOF(流体体积函数)法确定自由液面。采用稳态计算的结果作为瞬态计算的初始条件，计算模型如图1所示。

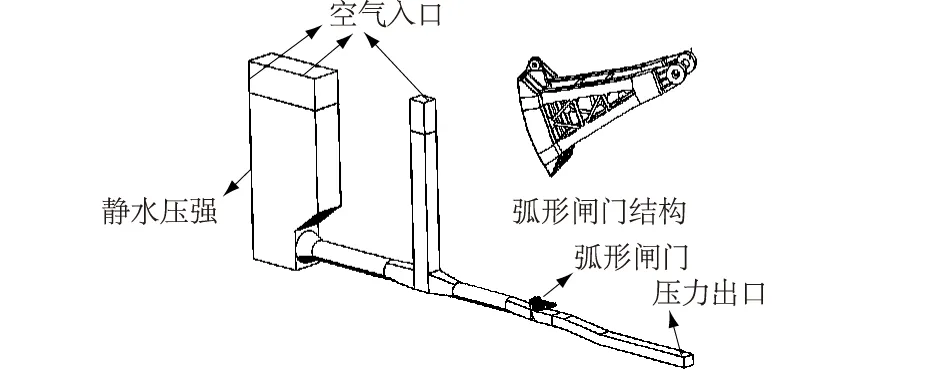
图1 数值模型示意图Fig.1 Schematic diagram of numerical model

图2为闸门在20%相对开度下的位移时程曲线，从图2(a)可以看出在同一开度下，闸门的侧向位移远小于水流向和垂向位移，与大广坝溢流坝段表孔弧形闸门[14]和五道水库泄洪洞工作闸门[15]原测资料结果一致，反映出侧向振动对闸门启闭力的影响较小。在图2(b)中，以20%相对开度下的闸门面板的径向振动为例，在闸门面板产生正位移时，促使闸门产生振动的力与水压力作用方向相同，相互叠加，并且支铰与转轴之间的挤压改变了摩擦系数与摩擦力臂，使闸门所需启闭力有所增加，反之在负位移处启闭力有所减小。但在闸门振动过程中，若以闸门振动负位移处作为闸门启闭力计算标准，则闸门在启闭过程中将会造成闸门振动负位移处启闭、正位移处卡阻这样一种爬振现象，因此需以振动正位移处的闸门压力作为启闭力设计标准，这样也就造成了闸门启闭所需要克服的摩擦力增大的现象。闸门若在超出启闭机启闭容量和安全系数的情况下运行，将造成闸门无法正常启闭，加速启闭设备的疲劳与磨损。

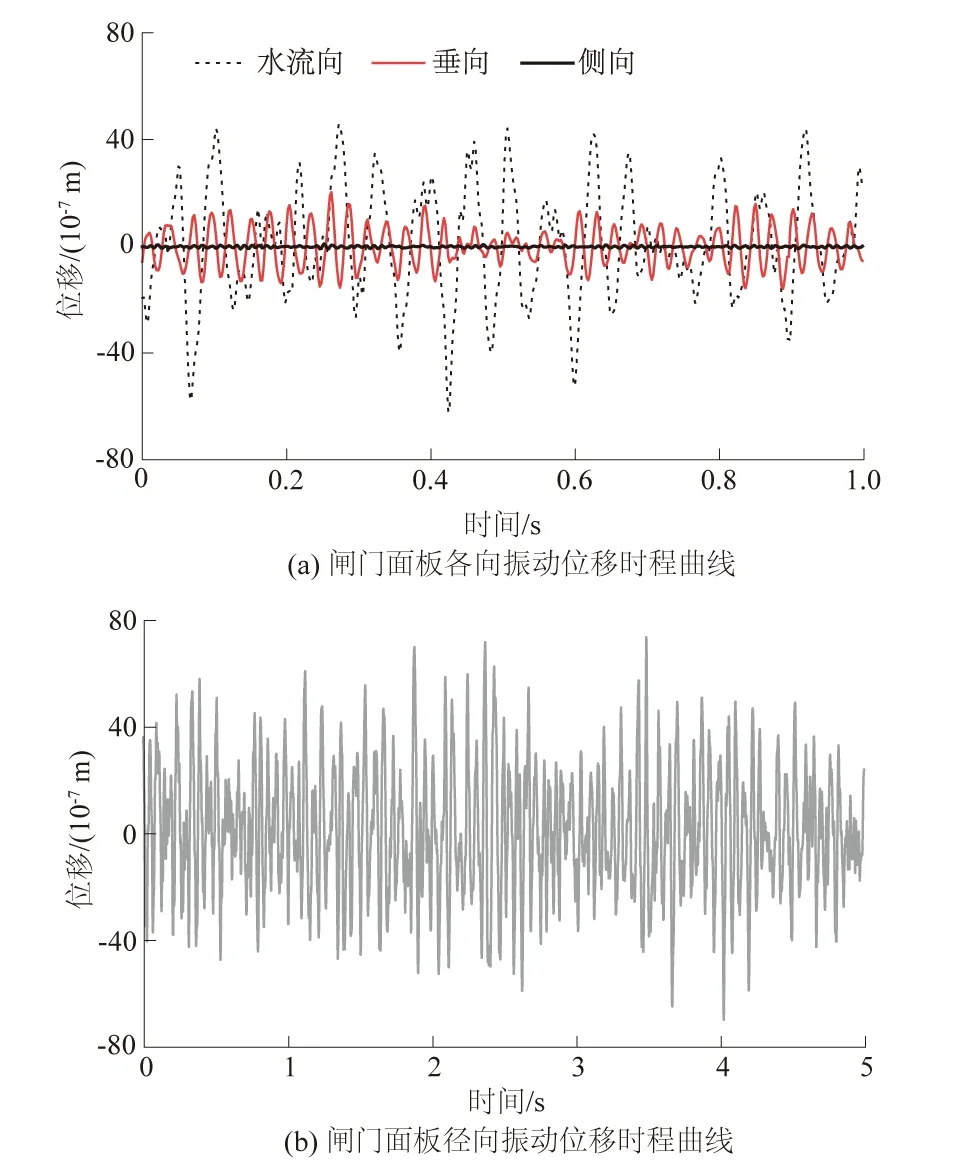
图2 20%相对开度时闸门面板振动位移时程曲线Fig.2 Time-histories of vibration displacement of radial gate panel at 20% relative opening degree

2.2 振动水压力计算

为探究振动对闸门面板受力的影响，现将弧形闸门简化为弹簧-阻尼体系，简化计算模型如图3所示，以径向合力方向为x轴，x轴与弧面交点为原点，与x轴垂直方向为y轴，建立直角坐标系。并做出如下假设：

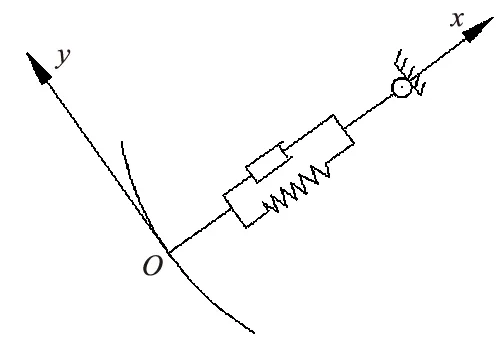
图3 弧形闸门简化计算模型Fig.3 Simplified calcula- tion model of radial gate

(1)闸门为微幅简谐振动，并忽略上游波浪的作用。

(2)下游无回流水对闸门的冲击。

(3)闸前水深恒定，水体向上游无限延伸。

基于以上假设，认为闸门泄流时受到的水压力P(t)为随时间变化的周期性荷载，可分解为均值静力部分P静和简谐波动部分P0，即

P=P静+P′sinωt；

(1)

式中：P′为简谐波动部分的幅值(kN)；ω为简谐波动的频率(Hz)。

由振动微分公式可知：

(2)

2.2.1 由简谐荷载引起的振动位移响应

式(3)为仅包含简谐荷载部分的二阶常系数非齐次线性微分方程，解的形式包括通解和特解。

(3)

式(3)的通解为：

(4)

式中：C1、C2为待定常系数；λd为考虑系统阻尼时的闸门的固有频率(Hz)。

振动系统阻尼的存在，造成振动位移和振动荷载存在一个相位差，因此该非齐次方程的特解为

y*(t)=C3sinωt+C4cosωt。

(5)

式中C3、C4为待定常系数。

由待定系数法和闸门振动的初始边界条件可求得待定常系数C1、C2、C3、C4，即

(6)

将式(6)分别代入式(4)与式(5)，两式相加可得到振动水压力荷载引起的闸门位移响应方程的通解：

Ansin(ωt-β) 。

(7)

由于系统阻尼的作用,式(7)的前一项会逐渐衰减，以至于逐渐消失；而后一项与结构的振动水压力有关，会使结构以振动水压力的频率振动[16]。

2.2.2 由压力均值荷载引起的振动位移响应

同理，将压力均值部分分离，振动方程写为

(8)

利用上述方法可得到闸门的静水压力引起的闸门的位移响应为

(9)

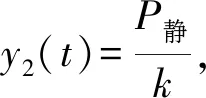
(10)

由徐汉忠等[17]所述，作用于结构上的动水压力在法向方向即闸上游平面的法向方向的数值等于此方向上的加速度与水密度和上游面面积的乘积，方向与其相反，因此作用于闸门面板的振动水压力与振动加速度的关系可表示为

则闸门的振动水压力P0为

(12)

式中：ρ为水的密度(kg/m3)；A为闸门面板浸水面面积(m2)。

2.3 流激振动下闸门启闭力计算

2.3.1 激振力引发的转动铰摩擦力

水流对面板的激振力通过闸门面板经支臂传递到支铰处，在闸门的逐步开启和关闭过程中，转换成影响闸门运行的动摩擦力。摩擦力矩为

(13)

式中：Fzd为动摩擦力(kN)；fsb为滑动摩擦系数；Mzd为摩擦力矩(kN·m)；r1为转动铰摩擦力臂(m)。

2.3.2 闸门自重与附加质量产生的重力矩

弧形闸门的启闭过程中的启闭力矩必须有一部分用来克服闸门自重和附加质量，假设闸门质量沿弧线方向均匀分布，则闸门中心与闸门支绞的距离l为

(14)

式中：r为弧形闸门半径(m);积分部分为对弧形闸门弧线进行曲线积分；φ为弧形闸门门叶对应弧度的1/2。

因此由闸门质量和附加质量产生的启闭力矩为

(15)

式中：MG为重力和附加质量产生的启闭力矩(kN·m)；G为闸门自重(kg)；G′为闸门附加质量(kg);r3、r4分别为闸门自重和附加质量的力臂(m)。

2.4 闸门启闭力

闭门力FW按式(16)计算，计算结果为正值时，闸门需要加重，结果为负值时，可以依靠自重正常启闭[1]。

FW=(1/R1)[nT(Mzd+Mzs)+MP-nGMG]。(16)

启门力FQ按式(17)计算,即

FQ=(1/R2)[nT(Mzd+Mzs)+MP+n′GMG]。(17)

式中：R1、R2分别为闭门力臂和启门力臂(m)；nT为摩擦阻力安全系数，可按规范取1.2；nG和n′G分别为计算闭门力和计算持住力、启门力时的闸门自重修正系数；MP为闸门垂直水动力产生的力矩(kN·m)；Mzs为闸门止水摩擦力矩(kN·m)。

3 模型验证

以玛尔挡泄洪放空洞弧形工作闸门的数值模拟结果作为验证依据。玛尔挡泄洪放空洞弧形工作闸门闸室洞段长28.0 m，工作弧门孔口尺寸为7.0 m×6.5 m(高×宽)，转轴半径为15 m。设计水头为100 m，闸门全关时挡水面积为54.28 m2，闸门质量m=5.74×105kg，计算时间步长取0.002 s。

3.1 位移验证

式(10)为振动位移方程(2)的通解，利用式(10)可以直接求解振动位移微分方程中的位移项。图4为式(10)计算结果与数值模拟振动位移对比情况，从中可知径向位移是随着开度的增大而不断减小的，反映出激振力随闸门开度的增加而减小。另外与数值模拟计算的结果对比发现，2种方法计算的结果在数量级上吻合良好，计算结果大致吻合。

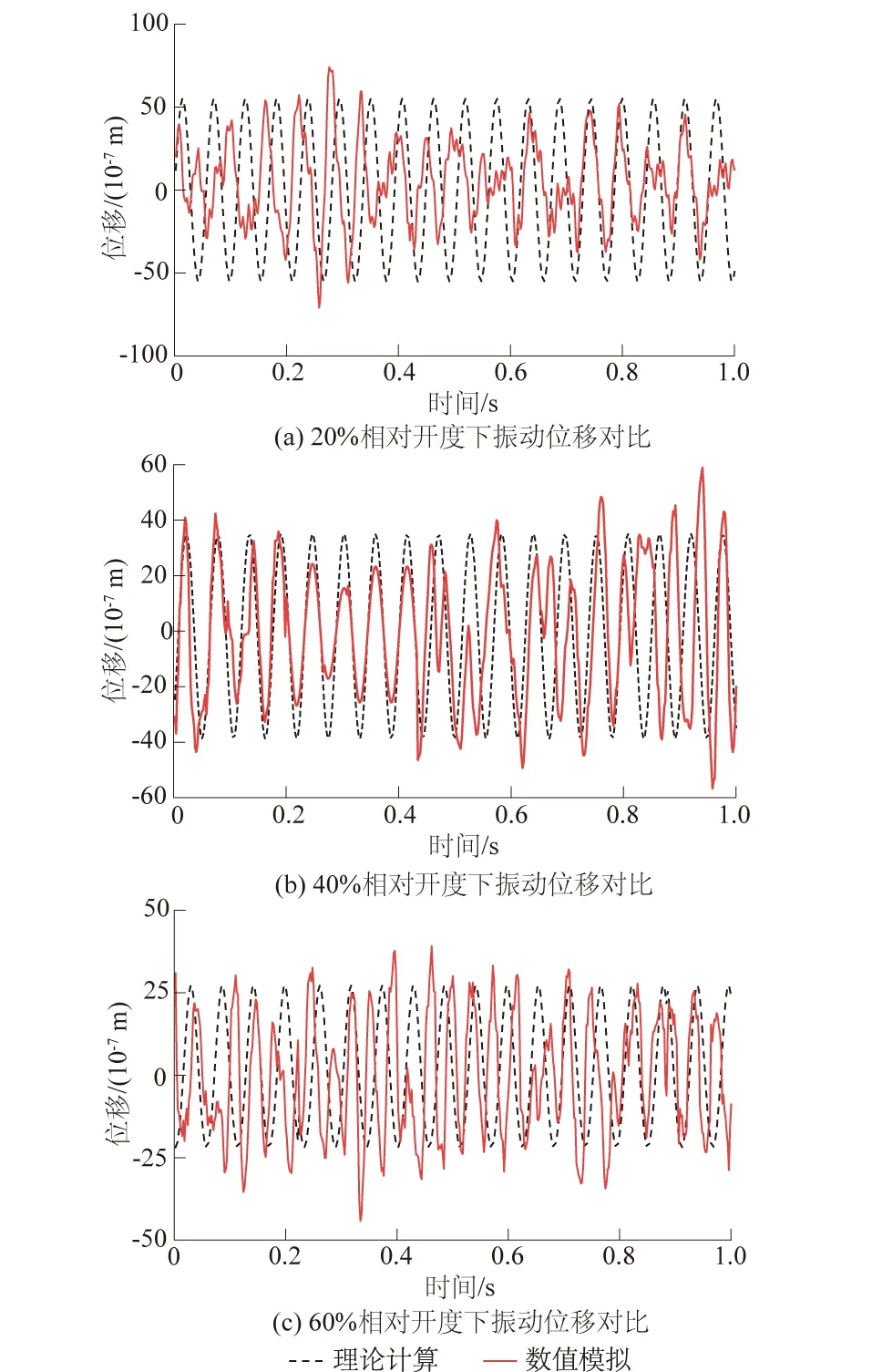
图4 不同相对开度下闸门整体振动位移对比Fig.4 Vibration displacements under different relative opening degrees

但由于本文构建的弹簧-阻尼简化力学模型与实际弧形闸门的刚度特性和质量分布有较大差别，因此理论计算结果与数值模拟结果存在差异，但仍可粗略估计闸门在实际运行过程中的振动位移变化情况。因此理论计算基本可以用于推测实际工程中的闸门面板的整体振动情况。

3.2 闸门面板压力验证

面板压力对比资料采用的是利用测点压力经点面转换公式得到的面压力。弧面的点面转换公式一般用于封闭圆形管道[18]，弧形闸门可认为是管道的一部分，通过对弧面点面转换公式的角度部分重新积分，使其适用于弧形闸门。改进后的点面转换公式为

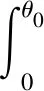
(18)

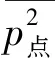
为得到闸门面板压力沿母线和环线的变化规律以及所受径向合力，在闸门的数值模型中，门叶部分分别布置3组沿母线和环线的压力测点，测点位置如图5所示。

图5 压力测点布置示意图Fig.5 Layout of pressure measuring points

推求测点压力的壁压相关系数[19]。根据点互相关系数，沿母线和环线方向的相关系数可分别由式(19)和式(20)求得。

(19)

(20)

式中：x,θ为测点编号；p′为测点压力脉动值。

通过测点压力得出环线和母线的相关系数接近于1，因此弧形闸门面板壁压的点压力之间呈现强线性关系，利用式(18)计算得到闸门面板压力，对比情况如图6所示。

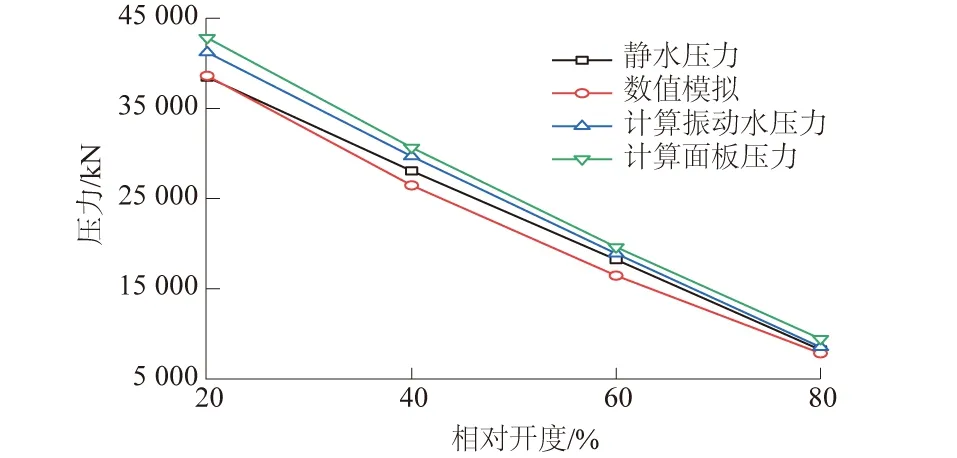
图6 闸门面板压力对比Fig.6 Comparison of gate panel pressure

从图6可知，闸前静水压力和单纯地进行流体的数值模拟计算得到的闸门面板压力都略小于考虑流固耦合时的闸门面板水压力，其中在小开度时这种差别比较明显，计算差异可以达到10.9%，随闸门开度的增大，计算差异有减小的趋势。此外，由弧形闸门的点面转化公式得到的面板压力与式(12)计算得到的水压力比较吻合，进一步验证了本文提出的振动水压力公式式(12)在弧形闸门上应用的准确性。

3.3 启闭力计算

表1为分别以振动水压力公式式(12)、点面转换公式式(18)和规范推荐计算公式3种方法为基础得到的启门力，其中式(12)是以基本的闸门属性利用理论公式推测的闸门面板压力，理论性较强，因此尤其在闸门设计前期具有较好的实用性；式(18)则是以实际测点压力为依据，利用点面转换公式转换为面板压力并结合启门力计算公式式(17)得到的启门力，与实际闸门运行中的面板压力结合紧密，因此本文采取这2种方法计算结果作为对比。

从表1可以看出由规范推荐计算公式得到的启门力偏小，特别是在小开度的情况下，差异达到5.14%，随着开度的增加，闸门振动减弱，计算差异逐渐减小，但仍存在偏小的现象，这种情况在启闭机的选择中是不利的。利用推导的振动水压力公式得到的弧形闸门的启门力与点面转换公式计算的启门力较为接近，可为闸门启闭力的计算和启闭机的选择提供参考依据。

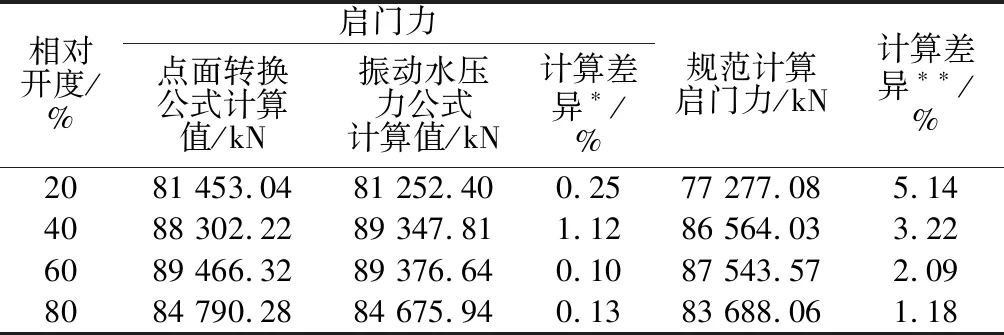
表1 3种不同方法计算启门力比较Table 1 Comparison of calculated opening force among three different methods

需要说明，由于启门力和闭门力的计算过程中关于激振力引发的转动铰摩擦力的计算方法相同，并且对比式(16)和式(17)可以发现，它们的不同主要在于闸门重力矩的加减，因此本计算方法也适用于闭门力的计算，同时也可以推测闭门过程也具有和启门过程相同的特性。但由于部分资料的缺失，故此处只选取了启门过程进行验证。

4 结 论

本文以玛尔挡泄洪放空洞弧形工作闸门为工程背景，采用理论推导与流固耦合三维数值模拟相结合的方法，从闸门振动产生的振动位移、振动面板压力以及引起的启闭摩擦力的变化3个方面分析了流激振动对弧形闸门面板受力以及启闭力的影响，得到结论如下：

(1)振动水压力计算公式以结构振动原理为基础，将结构稳定的闸门简化为弹簧-阻尼体系分析整体振动，体现了闸门面板压力、闸前水头以及闸门振动位移三者的关系，并在与实际工程的对比中验证了公式计算的可行性，以此可以推求在流激振动影响下的闸门面板受力以及闸门面板的振动位移，为闸门设计提供指导性建议。

(2)点面转换公式解决了在原型实测和物理模型试验中较难直接测量面板压力的问题，通过对柱面点面转换公式的改进，可在已知部分测点压力的情况下，由互相关系数推求实测和物理模型的弧形闸门面板整体受力。

(3)流激振动作用下的闸门面板压力明显增大，通过改进启闭力计算方法，将激振力纳入到闸门启闭力的计算中，结果表明在小开度的情况下由于流激振动的影响，闸门存在一个振动较严重的区间，在此区间内闸门启闭力明显增大，因此做好闸门启闭力的计算工作能更好地防止闸门在启闭过程中因启闭机容量不足造成的事故。

(4)本计算方法既适用于启门力的计算，也适用于闭门力的计算。但由于部分资料的缺失，只进行了启门力验证，未进行闭门力验证，这是本文的不足，还有待下一步研究。