基于面板数据分析方法的混凝土拱坝变形数据时空聚类模型

胡添翼

(上海市政工程设计研究总院(集团)有限公司 水利水运设计研究院,上海 200092)

1 研究背景

拱坝作为最常见的混凝土坝类型之一，是一种高次超静定空间壳体结构[1]，变形状态非常复杂，其安全状况非常值得关注。为了解拱坝安全状况，科研人员常对拱坝进行应力和变形监测，其中以变形监测数据最为直观可靠[2]。随着大坝安全监控理论发展，关于拱坝变形的分析和预测陆续涌现出许多成果[3-5]，如统计模型、混合模型等。目前针对拱坝的安全监测已经实现了对整个坝区的监测，在拱坝坝体及周围布设有大量变形监测点，如小湾拱坝安全监测系统已成为世界上最大的安全监测系统之一[6]。大坝海量的变形监测数据具有广阔的数据挖掘空间。

面板数据，指在时间序列上取多个截面，在这些截面上同时选取样本观测值所构成的样板数据；同时考虑样本时空性质的面板数据被称为时空面板数据。在多测点监测状况下，高拱坝测点变形数据同时包含多测点截面数据和单测点时间序列，具有时间、空间2种维度，因此可以被看作是一种时空面板数据[7-9]。时空面板数据聚类特性的挖掘和时空划分是时空数据挖掘的重要课题之一，其主要内容为根据时空数据的一些特征，对空间中的对象进行聚类或划分，使具有相似特征的对象能够被划分到同一个类别中去。近年来，面板数据分析方法已经在经济、农业、工程等领域获得发展，在大坝安全监控领域，传统的聚类分析已经得到了应用，如施玉群等[10]采用聚类分析方法描述多效应量之间的关联关系，建立了相应的融合诊断模型；陈继光[11]基于灰色关联度计算和模糊聚类分析原理，对变形数据进行了动态分析；陈毅[12]建立了基于基因表达式编程的大坝位移强度聚类分析模型，对大坝的整体变形规律进行分析。但这些研究一般仅仅考虑变形的时间性或者空间性，没有同时从时、空2个方面进行考量，不是典型的时空聚类分析。

本文基于时空数据挖掘领域的聚类方法，分析混凝土拱坝变形序列的变化过程，提取了变形序列的相似性特征；提出了混凝土坝变形数据不同时间截面、不同测点变形序列的3种相似性指标(绝对距离、增量距离、增速距离)，并计算了相应的综合距离指标，由此定量分析变形时间截面和变形空间测点的相似程度；利用Ward联结聚类方法，对混凝土坝变形时段及其相应变形区域进行划分；最终建立基于面板数据分析方法的高混凝土坝变形测点聚类分析模型，对混凝土拱坝变形状况进行综合分析。结合工程实例，对时空聚类模型的运用效果进行验证。

2 混凝土拱坝变形相似性特征

2.1 相似性特征选取

假设混凝土坝上3个不同位置的测点分别为A、B、C，其变形数值随时间的变化过程如图1所示。

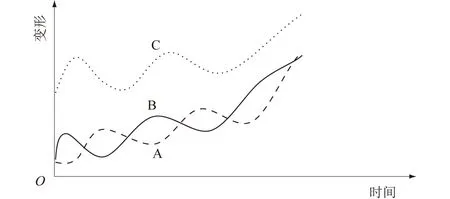
图1 不同变形数据的变化趋势Fig.1 Trends of deformation data at different monitoring points

图1中，如果单纯考虑每个测点的变形过程和变化趋势，A点和C点是最为接近的，应该被归为一类；如果单纯考虑变形的初始值和最终值(以及相应的平均值大小)，A点和B点虽然变化趋势不完全相同，但初始最终的变形值相同，应该被归为一类；如果从更大的范围来看，3个测点的变形值都有增大的趋势，也有可能被聚类为同一类。事实上，合理聚类方法应该综合考虑几种不同的变形特征，包括各个测点时段内变形值的变化数值、变化速率和变化趋势等各种变形特征需要被综合考虑。

综上，假设测点i在t时刻的变形为δit，本文着重考虑测点变形下面几个方面的变化特征。

(1)测点i在t时刻的变形值大小，记为xit，防止变形值差异过大的时间截面/测点被聚到一类,即

xit=δit。

(1)

(2)测点i在t时刻的数值变化，记为yit，防止变化值差异过大的时间截面/测点被聚到一类,即

yit=xit-xi,t-1=δit-δi,t-1。

(2)

(3)测点i在t时刻的数值变化幅度，记为zit，防止变化趋势差异过大的时间截面/测点被聚到一类,即

(3)

2.2 相似性特征的标准化

容易发现前文提取的3种变形特征量单位和数量级不一致，如果直接相加求所谓的“综合聚类指标”显然是不尽合理的，因此计算综合相异性指标之前需要对xit、yit、zit进行标准化操作，本文采用Z-score方法对基础指标进行标准化操作。假设共有N个监测点、T个时间截面的变形监测数据。以变形值xit为例，计算出所有xit的算术平均值(数学期望)，记为μx；计算所有xit的标准差，记为σx，则Z-score标准化公式为

(4)

标准化后的变量值在0上下波动，平均数为0，标准差为1。经过标准化操作之后，数据的取值范围得到了进一步限制，从而避免了量纲和取值范围所带来的影响。

3 混凝土拱坝变形时空相似性指标

本文运用聚类分析方法，一方面是为了对时间截面的测点变形状态进行聚类,从而实现拱坝变形时段划分；另一方面是为了在时段划分的基础上，根据测点变形序列对空间测点进行聚类从而实现变形区域划分。根据测量方式的不同，衡量变量的尺度一般分为间隔尺度、名义尺度和有序尺度[7]。考虑拱坝变形监测通常采用每周一测或每日一测等监测间隔，本文对于变形面板数据聚类分析的探讨仅仅基于间隔尺度。

假设用δit表示t时刻测点i的变形指标，用dij表示测点i和测点j变形之间的相似程度大小。连续变量常用的相似性指标有欧氏距离、欧氏距离的平方(简称SED)、绝对值距离和相关系数等。其中，SED因为不涉及到开方等计算，在计算上相对欧氏距离更加简便，本文所有的相异性指标均基于SED。以测点i和测点j在t时刻的变形值为例，其SED为

dijt(SED)=(δit-δjt)2。

(5)

式中δit和δjt分别表示测点i和j在t时刻的变形值。

3.1 时间序列划分指标

3.1.1 基本指标

为得到更加合理的相似性指标，本文从变形值、变形值的波动大小及其波动幅度3方面出发，定义了3种基本相似性指标，即不同测点的横截面绝对距离、横截面增量距离和横截面增速距离，详情如下。

(6)

式中：xnp=δnp；xnq=δnq。

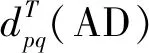
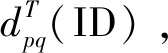
(7)

式中：ynp=xnp-xn,p-1；ynq=xnq-xn,q-1。

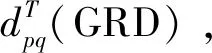
(8)

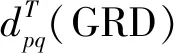
3.1.2 综合指标

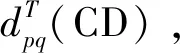
(9)

式中α1、α2、α3分别表示3种基本指标的权重系数，α1+α2+α3=1。

3.2 空间测点聚类指标

3.2.1 基本指标

参考针对时间序列划分的基本相似性指标，这里定义3种基本相似性指标，即测点聚类的测点绝对距离、测点增量距离和测点增速距离，详情如下。

(10)

式中：xet=δet；xft=δft。

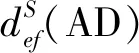
(11)

式中：yet=xet-xe,t-1；yft=xft-xf,t-1。

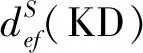
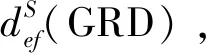
(12)

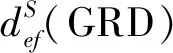
3.2.2 综合指标

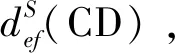
(13)

式中β1、β2、β3分别表示3种基本指标的权重系数，β1+β2+β3=1。

式(9)和式(13)中的权重系数可以根据实际情况进行主观或客观赋值，本文采用客观赋权熵权法来计算式(9)和式(13)中的权重系数[13-14]。

4 混凝土拱坝时空聚类模型

常见的聚类分析方法分为划分聚类和层次聚类。对混凝土拱坝变形数据进行聚类分析，因为事先不能确定聚类的数量，所以划分聚类方法并不适用于坝体测点聚类，层次聚类方法会相对更加合适一些。在实际应用中，Ward联结法的分类效果相对较好，应用也比较广泛，本文选用该方法进行聚类。聚类内容分为2部分：一部分是将时间序列离散化，根据每个时间截面大坝测点的变形情况对时间截面进行聚类，从而对变形时间序列进行有效划分；另一部分是将空间变形区域离散化，根据每一个划分时段测点的变形序列对测点进行聚类，从而对大坝的变形区域进行划分。

4.1 时间序列划分方法

(14)

(15)

当k确定时，要选择使W达到极小的分类。

基于Ward方法思想，对于包含T个时期、N个测点的大坝变形数据，可得到面板数据分类Gl内部Tl个不同时间截面的离差平方和为

(16)

若分为k类，则全局总离差平方和为

(17)

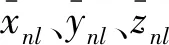
4.2 空间测点聚类方法

(18)

(19)

当v确定时，要选择使W达到极小的分类。

基于Ward方法思想，对于包含T个时期，N个测点的大坝变形数据，可得到面板数据分类Hu内部Nl个测点离差平方和为

(20)

若分为v类，则全局总离差平方和为

(21)

4.3 聚类数目的确定

聚类数目需要综合考虑谱系聚类树状图和测点变形状况进行最后的确定，实际操作中，往往通过阈值法确定层次聚类的数目。假设聚类过程共进行h次合并，第g次与最后一次分区的区域距离之比为

Sg=Wg/Wh-1。

(22)

式中：Wg为第g次分区全局总离差平方和；Wh-1为最后一次分区全局总离差平方和。

如果Sg与Sg+1相差较小，g与Sg-1相差较大，相应的Wg可以作为分区的阈值，这样就可以确定聚类的数目。

4.4 模型运作流程

本模型基于Ward层次聚类分析方法，主要分为时段划分和空间聚类2个部分。首先是变形时段划分，根据每个时间截面所有测点的变形相似性特征，对混凝土拱坝变形时间截面进行聚类分析，从而实现对变形序列的有效时段划分。在时段划分之后，基于每一个时段内测点变形序列的变化情况，再对混凝土拱坝的空间测点进行聚类分析，从而可以在空间上对混凝土拱坝的变形区域进行划分。模型运作流程如图2所示。

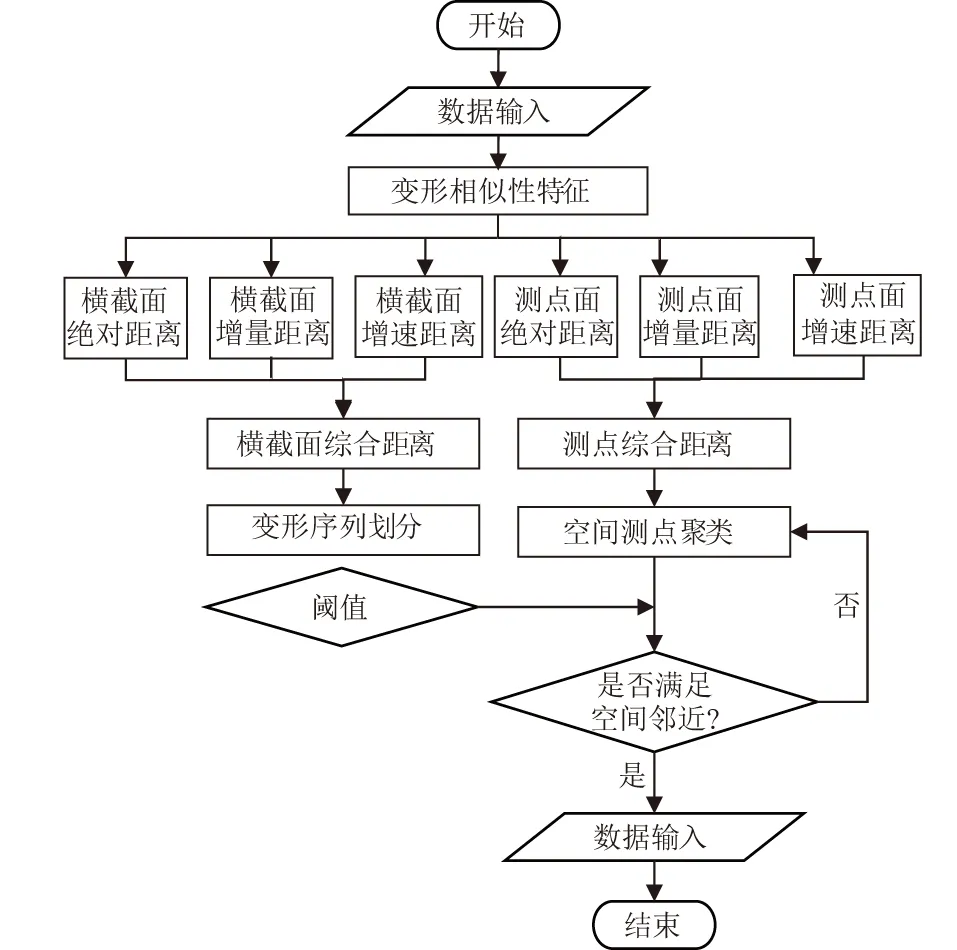
图2 模型运作流程Fig.2 Process of model operation

通过时空聚类分析模型，可以识别混凝土拱坝变形的相似时段和相似性区域，从而了解混凝土拱坝变形状态。

5 工程实例

为验证前文提出的时空聚类模型，以国内某300 m级混凝土拱坝变形情况为例进行分析。

5.1 工程概况

该拱坝坝体共设置了34个垂线测点监测大坝安全状况，测点具体布设情况如图3所示。

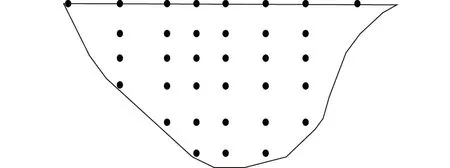
图3 某高拱坝变形测点布置示意图Fig.3 Layout of deformation monitoring points for an arch dam

以该拱坝34个测点从2014年5月1日开始的时间截面为300 d的径向变形数据和相关衍生指标共计30 600(3×300×34)个数据为基础，进行聚类分析。根据相关文献，库水位是拱坝位移变化的最主要因素，本文主要考虑水位变动条件。由于水位变动条件下拱坝变形大小受坝前水深影响最为显著[15-16]，本文主要考察坝前水深变化过程中变形数据的聚类情况，坝前水深和所有测点的平均变形随时间变化过程线如图4所示。

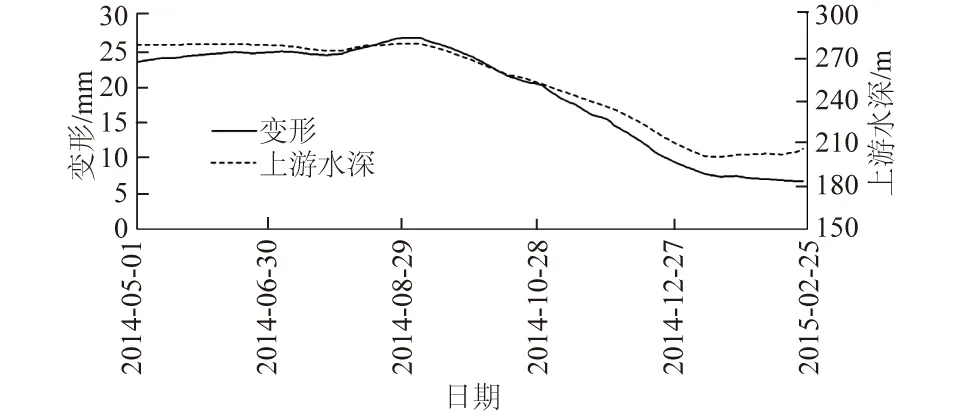
图4 水位变化及变形过程线Fig.4 Process lines of water level fluctuation and deformation

5.2 变形时段划分

首先对拱坝的变形时段进行划分。对不同时间截面的变形状态进行聚类分析，得到聚类谱系树状图，如图5所示(因时间截面太多，图中仅取10类以内的聚类结果)。

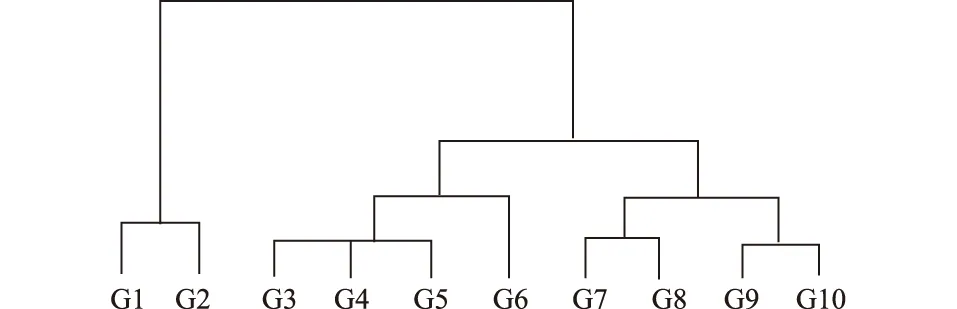
图5 拱坝变形序列划分谱系聚类树状图Fig.5 Tree plot of deformation sequence clustering for the arch dam

从聚类谱系树状图可以得知，变形时段可划分为3个主要时段：第1时段为2014年5月1日—2014年9月9日，此段时间内上游水深较深，大坝的整体变形比较平稳；第2时间段为2014年9月10日—2014年12月28日，此段时间内水深下降，大坝变形随水深下降不断减小；第3时间段为2014年12月29日—2015年2月24日，此段时间内水深较浅，大坝变形再次趋于稳定。模型划分的3个时段如图6所示。

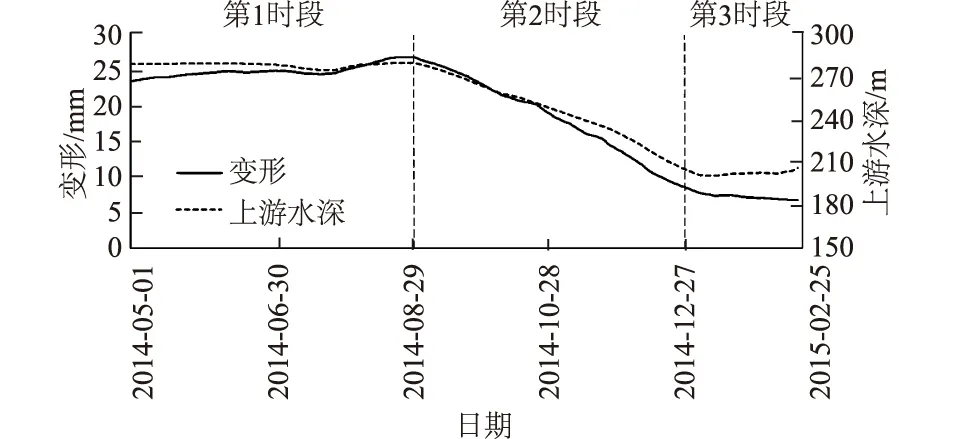
图6 拱坝变形时间序列划分结果Fig.6 Results of time series division of arch dam deformation

从图6可以发现，本模型划分出来的3个变形时段和大坝的整体变形情况以及上游水深的变化情况高度吻合，充分体现出每一个时段自身的特点，说明本模型对变形时段的划分是比较合理的。

5.3 空间测点聚类

根据前面聚类划分出来的3个变形时间段，分别在每一段时间段内根据测点的变形特征对测点进行聚类分析。

5.3.1 高水位期

针对高水位运行的第1时段，空间测点聚类结果如图7所示。

图7 拱坝高水位变形聚类分区Fig.7 Arch dam’s deformation zone under high water level

从测点聚类的情况来看，主要出现了4个比较明显的变形相似区域，其中Ⅰ区变形最大，Ⅱ区次之，Ⅲ区变形略小于Ⅱ区，Ⅳ区变形最小。变形最大区域集中在拱冠梁附近，呈长条状分布；其它聚集区域以坝轴线为中心对称分布。

5.3.2 水位消落期

针对水位不断消落的第2时段，空间测点聚类结果如图8所示。

图8 拱坝水位消落期变形聚类分区Fig.8 Arch dam’s deformation zone during water level drawdown

从测点聚类的结果来看，拱坝被分为3个变形相似区域，其中Ⅰ区变形最大，Ⅱ区次之，Ⅲ区变形最小。变形最大区域为大坝的中部；变形区域分布的对称性较好，但是Ⅱ区局部测点似乎出现了变形过大的问题。由此可以发现，随着上游水深的下降，拱坝变形最大区域已经开始出现下移，说明拱坝的应力状态已经出现变化。

5.3.3 低水位期

针对水位消落后低水位运行的第3时段，空间测点聚类结果如图9所示。

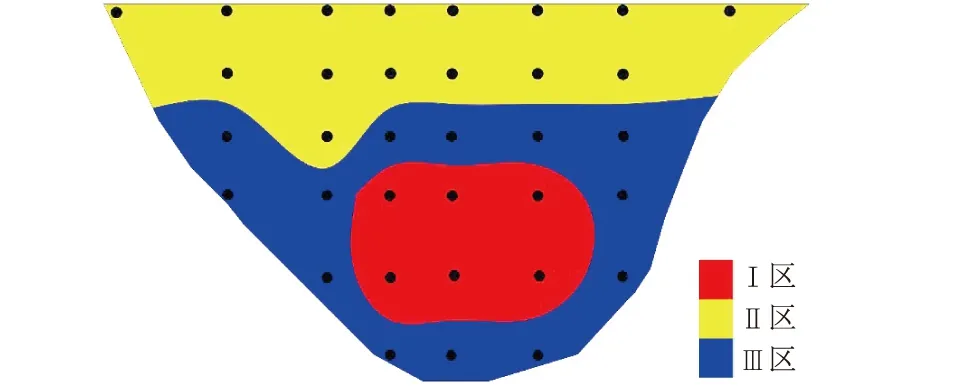
图9 拱坝低水位变形聚类分区Fig.9 Arch dam’s deformation zone under low water level

从测点聚类的结果来看，拱坝被分为3个变形相似区域，其中Ⅰ区变形最大，Ⅱ区次之，Ⅲ区变形最小。相较于上一个时段，变形最大的区域已经转移至拱坝的中下部，且该区域的面积有所减小；变形区域分布仍然呈高度对称，且之前变形过大的测点的变形已经有所减小。

6 结 论

本文根据3种变形数据的主要变化特征，从时段划分和测点聚类角度，构建了基于欧氏距离平方的3种基础相似性指标，在此基础上，提出了对应的综合相异性指标及相应的计算方法；基于Ward联结聚类法，分别提出了针对混凝土拱坝变形时段划分和变形空间测点聚类的聚类方法和步骤，建立了混凝土拱坝变形时空聚类模型；通过对某混凝土拱坝变形的时空聚类分析，验证了该模型的有效性。

根据工程实例的计算结果，可以看出：

(1)本文提出的混凝土拱坝变形特征以及由此提出的聚类相似性指标是比较合理的，能够综合反映大坝的变形状态；所采用的层次聚类方法计算简单快捷，可以对大坝的变形序列进行时段划分，对每个变形时段的空间测点进行聚类，从而了解大坝在不同时段的变形状态。

(2)不同时段特别是不同水位条件下的聚类分析会有比较明显的差异。从变形区域的分布情况来看，高水位和低水位等水位变化较小的时段区域分布的对称性良好，水位下降等水位变化时段区域分布的对称性相对差。因此，需要重点关注水位变化时期大坝的安全状况。