一种基于多尺度融合卷积神经网络的人群计数方法
蒋 俊,龙 波,高明亮,邹国锋
(1.西南石油大学计算机科学学院,成都 610500;2.山东理工大学电气与电子工程学院,淄博 255000)
随着城市人口的剧增,公共集会、大型体育赛事等人群聚集现象频繁发生。因此,快速、精准的人群计数方法对于人群分析、公共场所安全警示、群体异常事件预防等至关重要。此外,良好的计数算法也可以用于显微镜下微生物的计数、野生动物的数量统计等。
受人群遮挡、空间尺度和场景变化的影响,传统的基于检测和回归的人群计数算法计数准确度难以提高。随着深度学习在计算机视觉领域的深入研究和广泛应用,众多学者致力于深度学习框架下的人群计数方法研究,并提出了大量卓有成效的学习算法。这类算法能够有效提取图像特征,相较于传统的计数算法,计数准确度提升显著。但越来越深的网络结构意味着训练这些网络模型代价巨大,甚至训练完成的模型也受到电脑硬件的限制,无法广泛应用。
为了解决上述问题,现提出一种简易、高效的人群计数网络结构,多尺度融合卷积神经网络(multi-scale fusion convolution neural network,MSF-CNN),以期通过有效提取图像特征,解决人群之间的遮挡和空间尺度多变的问题。
1 相关工作
1.1 传统方法
由于训练数据的缺乏,早期的人群计数方法主要分为两类,即基于检测的方法和基于回归的方法。
基于检测的人群计数方法主要是通过检测场景中的行人个体对人数进行统计。文献[1]提出一种基于滑动窗口检测器的方法检测和统计人数。以文献[2-5]为代表的传统人群计数算法先从图像中提取行人的小波、边缘等图像特征,再利用这些特征训练一个分类器来检测人群并统计人群数量。此类行人检测方法对于人群分布稀疏的场景具有较好的效果。但是随着人群密度的提升,人群间的相互遮挡使得检测的准确性下降明显。文献[6-7]提出了通过检测身体的部分结构,例如头部、肩膀等身体结构来进行行人检测并统计人数。此类方法相较于基于行人整体检测的方法,具有较好的鲁棒性。然而在人流量大的复杂场景中,这类方法依然暴露出检测不准的缺点。
基于特征回归的人群计数的方法主要通过提取图像基本特征,建立特征和人数的回归模型来进行人数估计。以文献[8-10]为代表的基于回归的方法一般包括3个步骤:①通过前景分割将人群从图像中分割出来;②从分割得到的前景中提取纹理、边缘、面积和周长等特征;③训练一个回归模型,建立特征到人数的回归关系,进而估计人数。这类方法只能统计人数,而不能提供场景中人群密度的空间分布的情况,实际应用受到限制。人群特征的描述和回归模型的建立也是该类算法的难点。
1.2 基于深度学习的方法
近年来,以卷积神经网络(convolutional neural network,CNN)为代表的神经网络方法凭借其出色的特征表达能力,被广泛应用于计算机视觉领域[11]。研究者们开始使用深度学习方法解决复杂场景下的人群计数问题。
文献[12]提出了一种基于卷积神经网络的人群计数方法。该方法首先为某些特定的场景预训练一个网络,对于给定的新场景的图像,根据图像的透视信息对预训练网络进行微调以达到适应场景的目的。然而实际场景中的透视图不易获取,这极大地限制了该方法的适用性。Zhang等[13]提出的多列卷积神经网络(multi-column convolutional neural network,MCNN)网络结构,采用三列卷积核尺寸各不相同的卷积神经网络来提取图像中不同空间尺度的特征,通过对密度图积分求和估计人数,减少空间尺度的变化对计数结果的影响。在此基础上,为了使模型能够更好地适应图像人群规模和视角信息,Sam等[14]设计了一种选择器神经网络Switching-CNN,该方法根据图像块的内容信息选择预测结果最精准的CNN列生成该图像块的人群分布密度图并计数,取得了比MCNN[13]更好的计数效果。但因其复杂的网络结构,使得网络的训练过程变得不易实现。同时,网络中两次下采样降低了密度图的分辨率和准确度,在一定程度上影响人群密度估计和人群场景分析等其他更高层次的认知任务。
2 方法的设计与实现
采用卷积神经网络进行人群计数主要有两种方式:一是直接建立输入图像和估计人数的映射关系模型,通过此模型估计人数;二是先通过CNN提取输入的图像的特征得出该图像的人群分布的密度图,再对密度图积分求和,进而统计人数。第一种方法较为直接,但缺乏人群分布的空间信息,无法完成人群密度估计和人群场景分析等更高层次的认知任务。因此,采用第二种方式来进行人群计数。此类方式中,密度图质量的好坏直接决定了计数的精准度。生成高质量、高分辨率的密度图像成了此类算法的核心。
2.1 网络框架
图1为提出的多尺度融合卷积网络结构。其中,‘Conv_m×n’表示包含n个大小为m×m卷积核的卷积操作;‘pooling’表示感受域为2×2的MaxPooling操作;‘Cat’表示特征合并操作;‘Transposed Conv’表示用来扩大特征图尺寸的反卷积操作,该反卷积的stride参数设置为2,output_padding参数设置为0。特征提取部分末端的1×1的卷积层未在图中呈现,与特征融合处采用拼接操作将深度分别为8、10和12的特征图合并成深度为30的特征图,不涉及卷积操作。
网络以真实人群场景作为输入,输入规格对像素大小没有限制。从真实人群场景中学习端到端的映射,输出预测密度图。网络的结构主要可以分为两个部分,即特征提取部分和特征融合部分。

图1 多尺度融合卷积神经网络结构Fig.1 The architecture of MSFCNN
MCNN[13]利用三列不同尺寸卷积核的CNN有效提取图像中不同尺度的特征。使得生成的模型能够很好地适应图像因多变的拍摄角度和分辨率大小而产生的不同的人头尺寸。因此,MSF-CNN与MCNN类似,首先采用尺寸为9×9、7×7和5×5的卷积核提取原始图像的人群宏观特征,然后依次采用尺寸较小的卷积核提取高级特征。为了缩减网络参数,提高训练收敛速度,借鉴了GoogLeNet中Inception结构的参数设置方法在每一列的最后加一层卷积核为1×1的卷积层[21]。网络的特征融合部分采用卷积核尺寸分别为7×7、5×5和3×3的三层卷积结构对特征提取部分提取到的特征以合作的方式进行融合。最后采用1×1的卷积核将特征图映射到密度图。网络的特征提取部分使用了两次MaxPooling操作以减少网络的参数和训练的运算量,但也使得网络提取到的特征图和生成的密度图尺寸缩减到了原始图像的1/4。为了提高密度图的分辨率以便更加准确地统计人数,采用了一层2×2的反卷积操作将密度图像的尺寸扩大到原来的二倍。
2.2 训练过程
与Switching-CNN14等复杂网络相比,此处提出的网络更加易于搭建,没有纷繁复杂的训练过程。网络包含较少的网络层数和卷积核个数,这意味着网络具有较少的参数和更快的收敛速度。值得注意的是,网络的特征提取部分采用了两次池化和一次反卷积操作,因此需要将训练的真实密度图缩小到原来的1/2后再生成用于模型的训练。而对于输入的图像,网络可以输入任意大小的原始图像以避免失真和原始信息的丢失。
2.2.1 生成密度图
MSF-CNN通过生成密度图积分求和来统计人数,训练学习前需要将训练样本中带有人头标注的数据转化成人群分布密度图。故采用脉冲函数卷积高斯核的方式来生成密度图。
在一张标注有N个人头的图像中,若xi像素处有一个人头标注,用脉冲函数可以表示为δ(x-xi),则整张图像的人数可以表示为
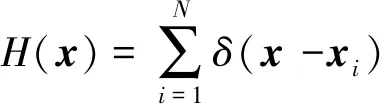
(1)
式(1)中:N为图像中标注点数量;x为图像矩阵;xi为图像中的标注点。假设xi是图像平面的独立样本,通过与高斯核函数的卷积操作将其转化成连续的密度函数:
F(x)=H(x)*Gσ(x)
(2)
式(2)中:Gσ(x)为高斯核滤波器函数;*为卷积运算。如果在每个人头点周围人群是均匀分布的,则通过该人头点与它的k个近邻的平均距离可以合理估算由于图像拍摄视角引起的几何偏差。因此需引入基于人头大小的分布参数σ,而密集人群中人头大小通常和最近两个人间的距离有关。文献[13]提出基于与临近标注点的平均距离决定高斯分布的参数,即几何适应的核。因此密度函数可以表示为
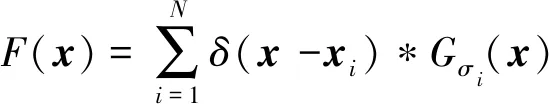
(3)

图2 测试图像及生成的基准的密度图Fig.2 Testing images and the corresponding ground truth density maps
2.2.2 损失函数
欧式距离损失函数作为模式识别中最为常用的损失函数之一,具有旋转不变性和平移不变性等优点。因此采用欧氏距离来度量估计的密度图与真实密度图之间的差异。损失函数定义为
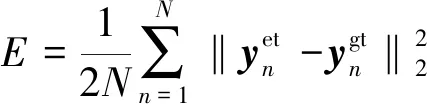
(4)
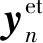
3 实验与分析
3.1 实验环境
多尺度卷积融合网络的运行环境为:CPU Intel E5-2670,显卡GTX 1080 Ti(显存64 G),操作系统Linux Ubuntu 16.04,深度学习框架PyTorch。为了提高模型拟合速度,网络训练参数设置如表1所示。

表1 网络训练参数设置列表Table 1 Training parameters of MSF-CNN
3.2 评价标准
在人群计数问题中,计数误差主要采用两个指标进行度量,即平均绝对误差(MAE)和平均均方误差(MSE)。其定义为
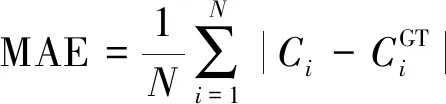
(5)

(6)

3.3 ShanghaiTech数据集
ShanghaiTech数据集总共包含1 198张标记图片,总标记人数达到330 165 人,数据集分为part A和part B两部分。part A部分300张用于训练,182张用于测试;part B部分400张用于训练,316张用于测试。part B部分的图片相较于part A部分的图片人群分布更为稀疏,但人群分布变化较大。同时将训练集中的每张图片选取9个不同位置的图片块,每个图片块的大小为原始图片的1/4,前4张图片块包含4个不重叠的图块,而其他5个图片块从输入图片中随机选取,扩展后数据集样本量是原数据集的9倍。
在ShanghaiTech数据集上的实验结果如表2所示。与近年来主流的人群计数方法相比较,本文方法在part A上的MAE和MSE达到最好。其中与MCNN[13]相比分别降低了16.4和30.6,与彭山珍等[18]提出的方法相比,MAE降低了3.4。与TDF-CNN[17]相比MSE降低了2.5。在part B数据集上,本文方法与MCNN[13]相比分别降低了3.9和6.3;与最好方法的MAE和MSE仅相差2.5和3.9。
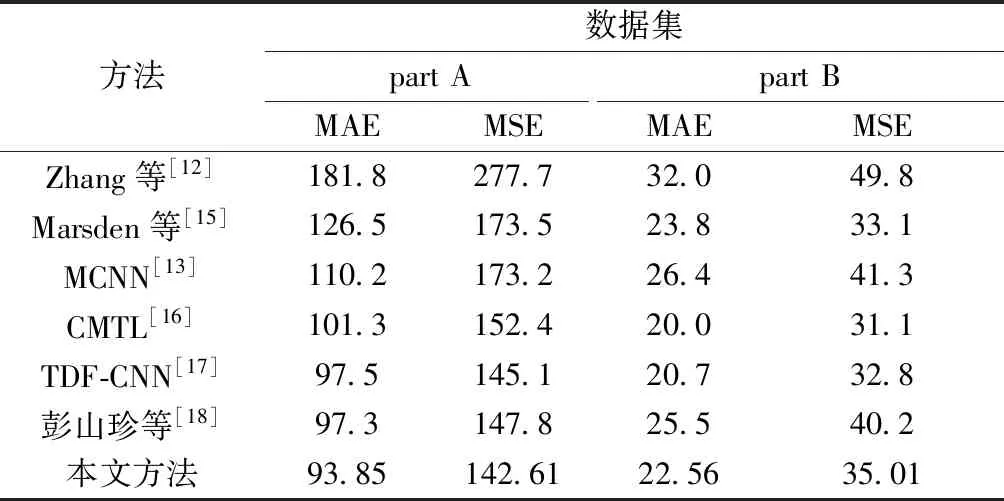
表2 ShanghaiTech数据集上的结果对比Table 2 Comparative results on ShanghaiTech datasets

图3 测试图片的真实密度图和估计密度图Fig.3 Testing images and the corresponding ground truth and estimated density maps
以上结果表明MSF-CNN能有效提取图像特征和适应人群密度、场景的变化,明显优于MCNN方法,对不同场景下的人群计数具有较好的准确性。图3展示了在ShanghaiTech数据集上算法预测的密度图和真实密度图。
3.4 UCF_CC_50数据集
UCF_CC_50数据集是一个极具挑战性的数据集,仅包含50张图片,却标注有63 974 人。平均每张图片标注1 280人,单张图像标注人数从94人到4 543 人不等。UCF_CC_50对算法的性能有极大的考验。
对UCF_CC_50数据集采用了与ShanghaiTech数据集相同的数据增强方式来扩展原始数据集。使用五折交叉验证对算法进行评价[11]。结果如表3所示。
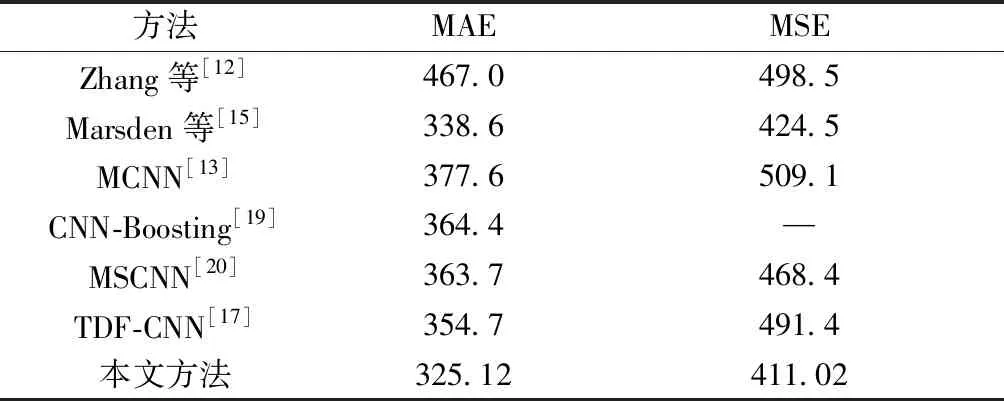
表3 UCF_CC_50数据集上的结果对比Table 3 Comparative results on UCF_CC_50 datasets
实验结果表明,本文方法在MAE和MSE上与MCNN[13]相比分别降低了52.4和98.0,也优于其他人群计数方法。此外,本文方法对于存在不同视角失真的复杂场景,也表现出了良好的鲁棒性。
3.5 模型分析与参数比较
3.5.1 模型分析
为了验证三列特征提取网络L1~L3对模型计数精度的影响,分别采用特征提取网络L1、L2、L3和特征融合部分C的不同组合进行实验。表4展示了单个特征提取网络和这些组合在ShanghaiTech Part A数据集上的实验结果,由此可见本文方法中网络结构的有效性。

表4 不同网络结构组合精度比较Table 4 Accuracy comparative results with different network structures
3.5.2 参数比较
通常情况下卷积神经网络模型参数数量直接决定了模型的复杂度[22]。模型复杂度在很大程度上影响该模型的运行时性能,网络模型空间复杂度的计算式[23]为
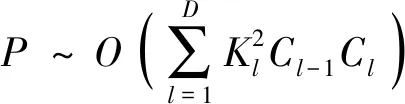
(7)
式(7)中:P为模型空间复杂度;K为卷积核的尺寸;C为通道数;D为网络深度。
自CNN出现以来,研究人员在优化卷积神经网络结构和改善模型复杂度方面做了大量的工作,意在用包含较少参数的简单模型完成较为复杂的任务[24-25]。复杂度与输入数据大小没有关系。本文方法与近年来的一些人群计数方法在模型参数数量大小比较如表5所示。由此可见,本文方法提出的网络模型含有较少的参数,是一种结构简单且性能良好的网络模型。

表5 不同方法的模型参数比较Table 5 Comparative results on model parameter size with different methods
4 结论
为了解决人群计数中存在的人群互遮挡、空间尺度多变和复杂深度网络难以训练的问题,提出了一种基于多尺度融合的卷积神经网络人群计数方法。网络结构由特征提取和特征融合两部分构成。特征提取部分能够有效提取图像中不同空间尺度的人群特征;特征融合部分以合作的方式对提取到的特征进行融合,进而建立输入图像与密度图的映射关系。同时,采用相对更少的网络层数和卷积核个数,利用反卷积来提高预测密度图像分辨率。最后,实验验证了本文方法的有效性,在ShanghaiTech和UCF_CC_50数据集上与近年来的多种流行的人群计数方法相比。结果表明本文方法易于训练,具有良好的准确性和鲁棒性。
在后续工作中,将继续优化网络结构,并在图像透视和损失函数等方面开展深入研究。

