三角反铁磁材料Mn3Z(Z=Ga,Ge,Sn)的磁性和输运性质
张强强,柳祝红,马星桥,刘恩克
(1.北京科技大学物理系,北京 100083)(2.中国科学院物理研究所 北京凝聚态物理国家实验室,北京 100190)
1 前 言
当前的自旋电子器件主要基于铁磁性材料。反铁磁材料由于具有零磁矩或者非常小的磁矩,没有杂散场,不受外磁场干扰,故具有更高的稳定性。同时,反铁磁材料具有更快的响应速度(响应频率高)、更低的能耗以及更高的存储密度等特性,为发展下一代非易失性低功耗反铁磁存储器件提供了契机,可能对磁性随机存储器、人工神经网络、太赫兹存储器件和探测器等领域产生重大影响。
在众多的反铁磁材料中,非共线反铁磁材料Mn3Z(Z=Ga,Ge和Sn)中出现了许多引人关注的新颖物性,如反常霍尔效应(anomalous Hall effect,AHE)、自旋霍尔效应(spin Hall effect, SHE)、拓扑霍尔效应(topological Hall effect, THE)、反常能斯特效应(anomalous Nernst effect, ANE)等,已经成为当前凝聚态物理研究中的前沿与热点。
六角Mn3Z(Z=Ga,Ge和Sn)合金具有DO19型结构,如图1a所示,空间群为P63/mmc(No.194)。其中Mn原子占据(1/6,1/3,1/4)位置,Z原子占据(1/3,2/3,3/4)位置。在六角Mn3Z结构中,两种镜面对称的Mn3Z反铁磁平面沿着c轴方向叠加嵌套,每一层的Mn位形成一个由共享等边三角形组成的二维网格,即Kagome晶格[1]。在六角Mn3Z(Z=Ga,Ge和Sn)合金中,所有Mn原子的磁矩都位于ab平面,形成一个手性自旋结构,其矢量手性与通常的120°结构相反。Mn3Z合金已经被证明具有多种类型的非共线反铁磁结构[2-6]。早在1990年Brown等[7]发现Mn3Z有两种最有可能的磁结构排列,分别如图1b和1c所示[2],这两种磁结构具有相反的手性,且磁结构数据与实验测量值高度吻合。因此,当前对Mn3Z(Z=Ga,Ge和Sn)合金的研究既有采用图1b型磁结构的,也有采用图1c型磁结构的。
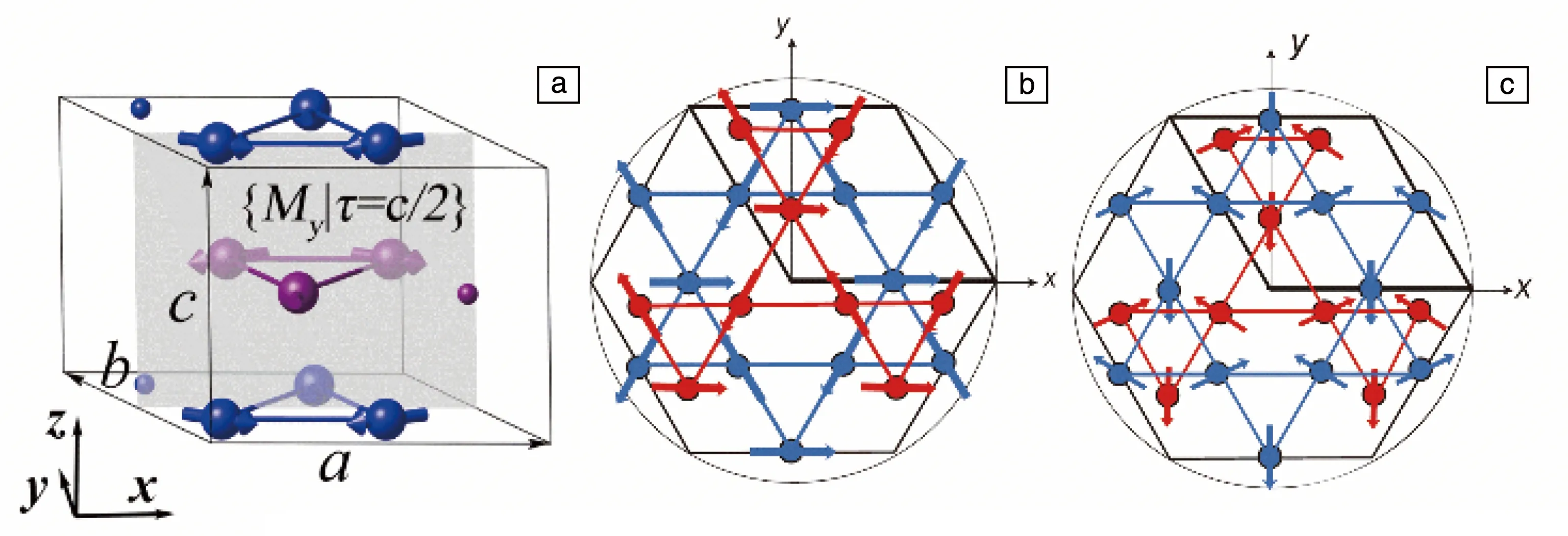
图1 六角Mn3Z的晶体结构(a)[1]; Mn3Z合金的两种不同的磁矩构型(b, c)[2]Fig.1 Lattice structure of hexagonal Mn3Z(a)[1];the two different magnetic moment configurations of Mn3Z alloy, respectively(b, c)[2]
由于六角Mn3Z合金在基态下会展现出极小的净磁矩,表现出弱铁磁性,实际上并不算严格的反铁磁材料。Mn3Z中倒三角形磁矩排列具有正交对称性,每个Mn原子组成的三角形中只有一个Mn原子的磁矩平行于局域易磁化轴,因此另外两个自旋磁矩向局域易磁化轴的倾斜被认为是Mn3Z弱铁磁性的来源[4, 8]。
在凝聚态物理中,材料所展现的许多物性都与其电子结构密切相关,而电子的行为反映在能带结构中。
Mn3Ga、Mn3Ge和Mn3Sn的能带结构看起来非常相似,如图2所示[1]。由于Ga原子的价电子数相对于Ge和Sn原子少一个,因此Mn3Ga的费米能级(EF)相对于Mn3Ge和Mn3Sn的向下移动约0.34 eV。在Mn3Z合金中,能带结构在EF附近具有线性交叉,产生外尔(Weyl)点。Weyl点是动量空间中的奇点,可以被理解为磁单极子。这些点成对出现,并且产生特有的表面性质,即所谓的费米弧。Weyl点处具有极强的贝利(Berry)曲率磁通分布,这个Berry曲率可以看作是动量空间中的赝磁场。这3种合金的能带中价带和导带在EF附近多次交叉,产生多对Weyl点,其中大部分为II型(II型Weyl点与I型Weyl点的区别在于其能带中Weyl锥在某个动量方向上发生倾斜)[9]。Weyl点的位置和手性与磁晶格的对称性一致。其次,在高对称点K和A处可以发现看似相似的能带简并点,如图中红色圆圈所示。
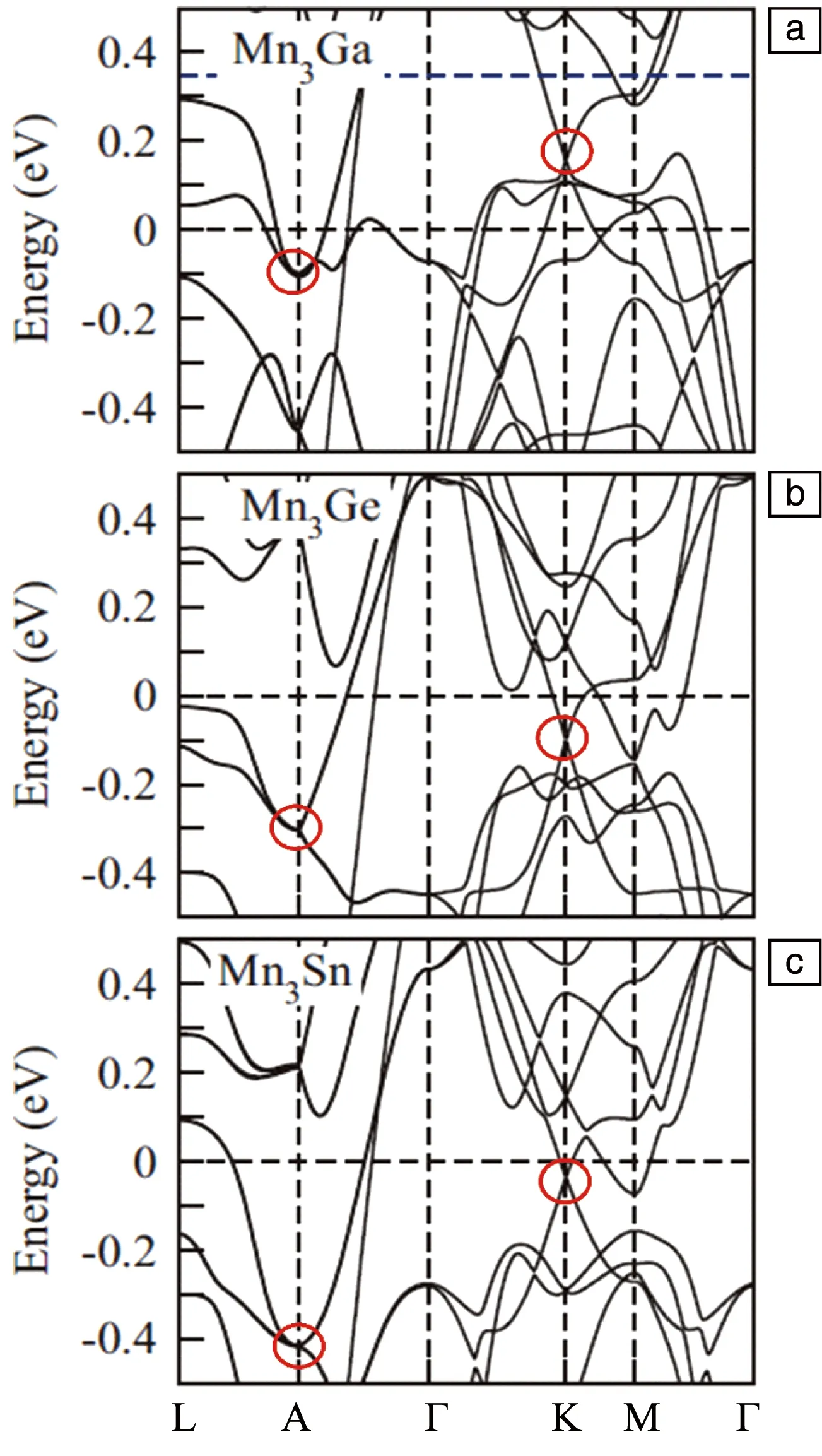
图2 Mn3Ga(a)、Mn3Ge(b)和Mn3Sn(c)的能带结构[1]Fig.2 Electronic band structure for Mn3Ga(a),Mn3Ge(b) and Mn3Sn(c)[1]
有趣的是,部分Mn3Z合金除了可以形成DO19型六角结构之外,还可能形成DO22型四方结构或DO3型哈斯勒(Heusler)立方结构。例如,Mn3Ga在623 K的温度下退火会形成DO22型四方结构,在883 K的温度下退火会形成DO19型六角结构,在1073 K的温度下退火则会形成DO3型Heusler立方结构[10]。DO22型Mn3Ge在大约800 K的温度下会向DO19型六角结构转变[11]。因此,为了确保合金可以以稳定的DO19型六角结构结晶,合适的热处理是必要的。
2 六角Mn3Sn合金的输运性质
2.1 Mn3Sn中的AHE
AHE是磁性材料中比较常见的输运效应,由于其在自旋电子学器件材料方面具有潜在的应用前景,使其迅速成为材料科学等领域的研究热点之一。一般认为,铁磁性材料的AHE与其磁化强度成正比。由于反铁磁材料缺乏净剩磁矩,普遍认为反铁磁材料中不会出现AHE。
后来的研究表明,AHE起源于两种不同的机制:一种是由杂质原子散射所引起的外禀散射机制,包括边跳机制和螺旋散射机制;另一种是晶体能带的Berry曲率所驱动的内禀机制,与外部散射无关。Berry曲率相当于布里渊区中的赝磁场,可以使电子获得一个额外的群速度,从而产生内禀反常霍尔电导(anomalous Hall conductivity, AHC)。内禀AHE仅与材料的能带结构相关,这为在反铁磁材料中发现AHE提供了条件。Mn3Sn在EF附近的Weyl点处所具有的Berry曲率磁通分布是导致该材料出现大的反常霍尔电导的关键。
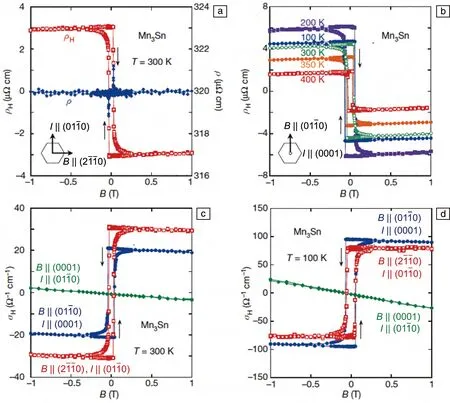
图3 Mn3Sn单晶的AHE测量曲线[12]Fig.3 Magnetic field dependence of the AHE in Mn3Sn[12]
Mn3Sn的可变磁结构会影响费米面附近的能带结构,进而影响其AHE。为了更好地对AHE进行调控,北京科技大学陈骏团队对多晶Mn3Sn复杂的磁结构及其与AHE的相关性进行了研究[13]。
研究发现,Mn3Sn在不同的外部磁场下带场冷却(field-cooling, FC)的得到测量曲线在磁转变温度TS=190 K时存在明显的磁相变(图4a)[13]。早期研究表明,Mn3Sn在奈尔温度TN=420 K以下是三角反铁磁结构[14],并且三角反铁磁结构在TS温度下转变为非公度自旋结构[15]。在自旋玻璃转变温度Tg=50 K的温度以下,磁化强度随着温度的降低而升高,这主要是由于低温下的自旋玻璃态引起的[16]。外加磁场的大小几乎不影响FC曲线的形状和磁转变温度的大小,并且外加磁场强度的增加只导致Mn3Sn磁化强度的小幅增加,表明Mn3Sn中的磁结构非常稳定。图4b为Mn3Sn在不同温度下的M-H曲线,可以看到所有温度下的M-H曲线在6000 Oe的外场下都没有达到饱和。当温度高于200 K时M-H曲线展现出明显的磁滞,表明非共线反铁磁Mn3Sn存在弱铁磁性。
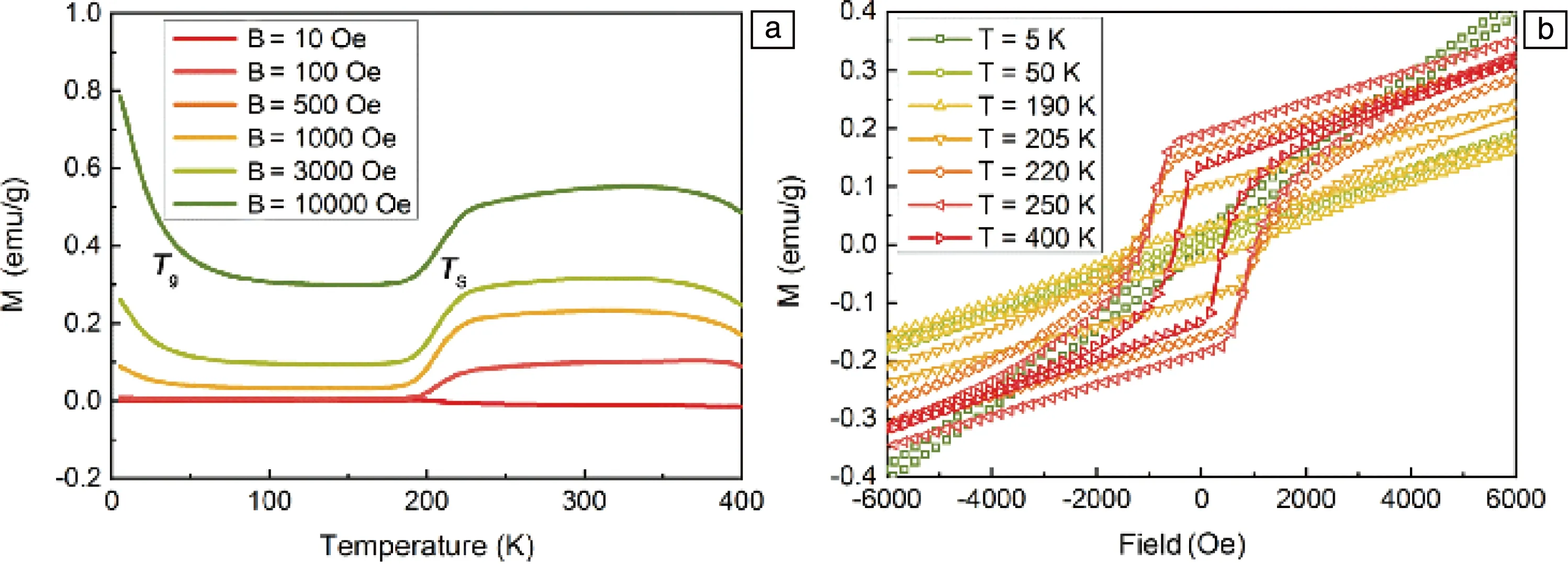
图4 Mn3Sn在不同外加磁场下带场冷却得到的热磁曲线(a),Mn3Sn在不同温度下的磁滞回线(b)[13]Fig.4 Magnetization as a function of the external magnetic field and temperature[field-cooling (FC) modes](a), hysteresis loops of Mn3Sn at different temperatures (b)[13]
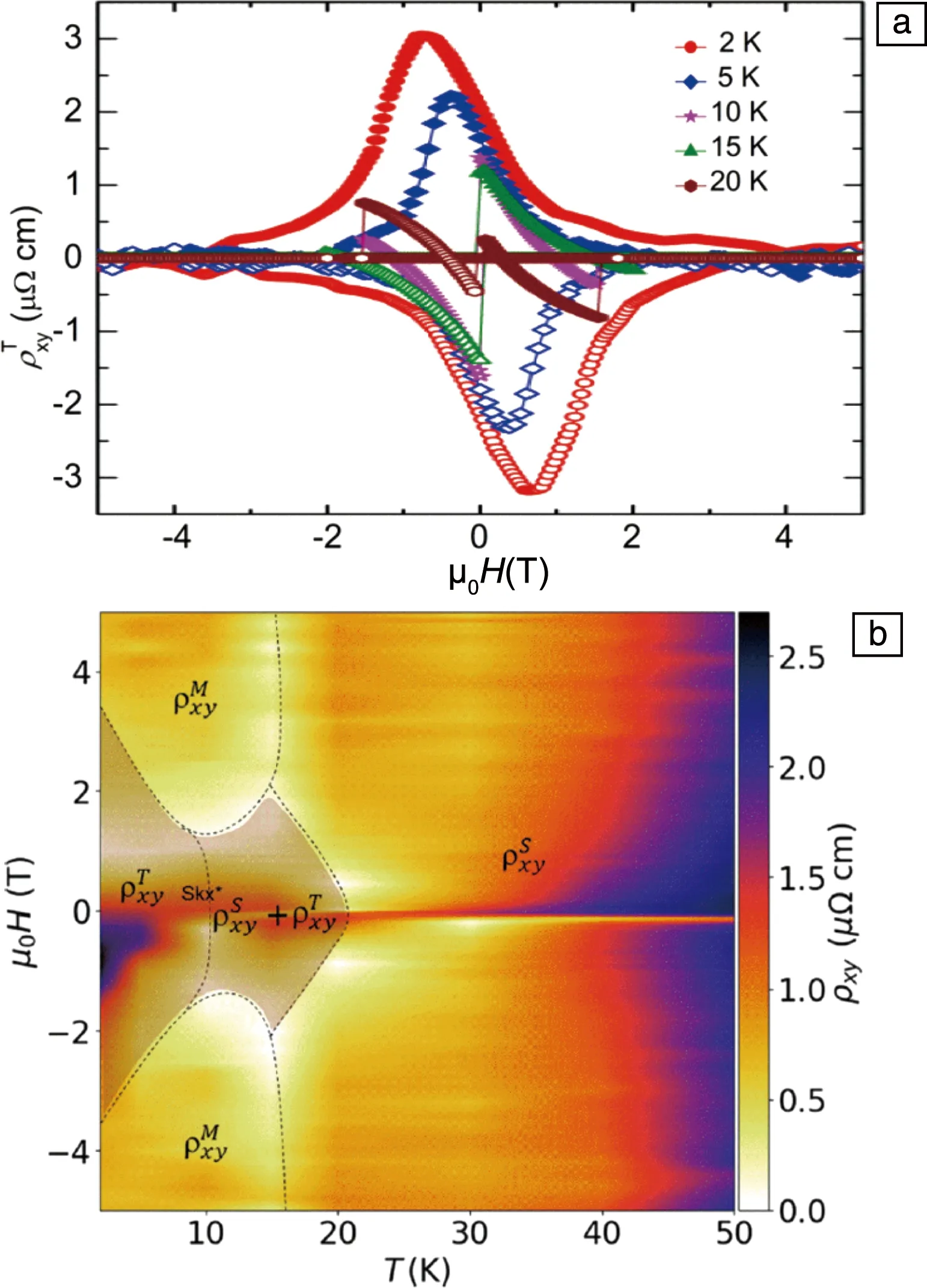
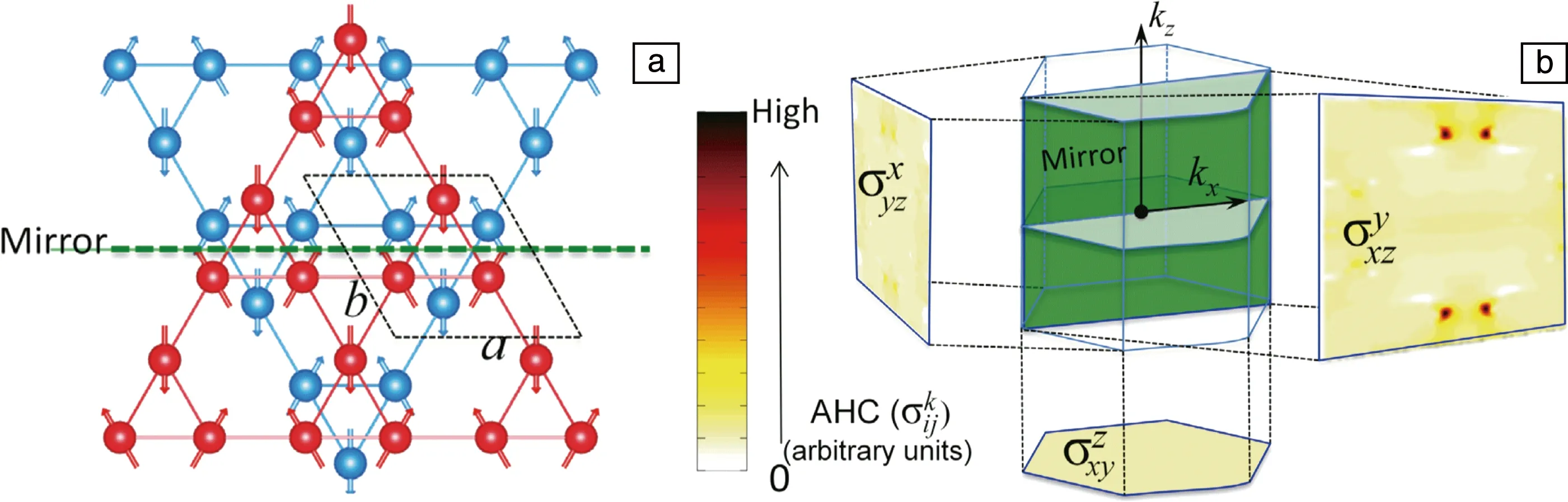
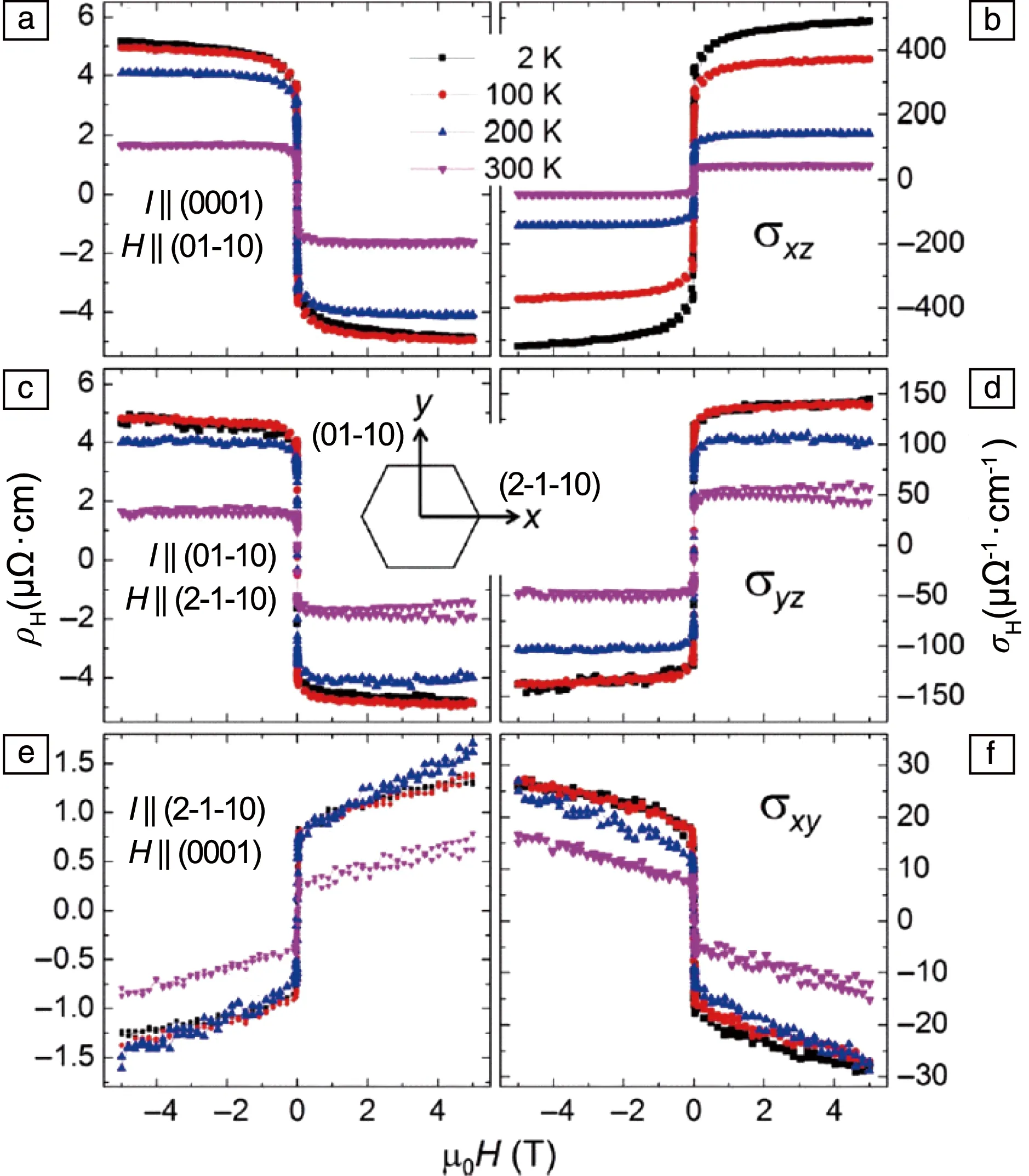
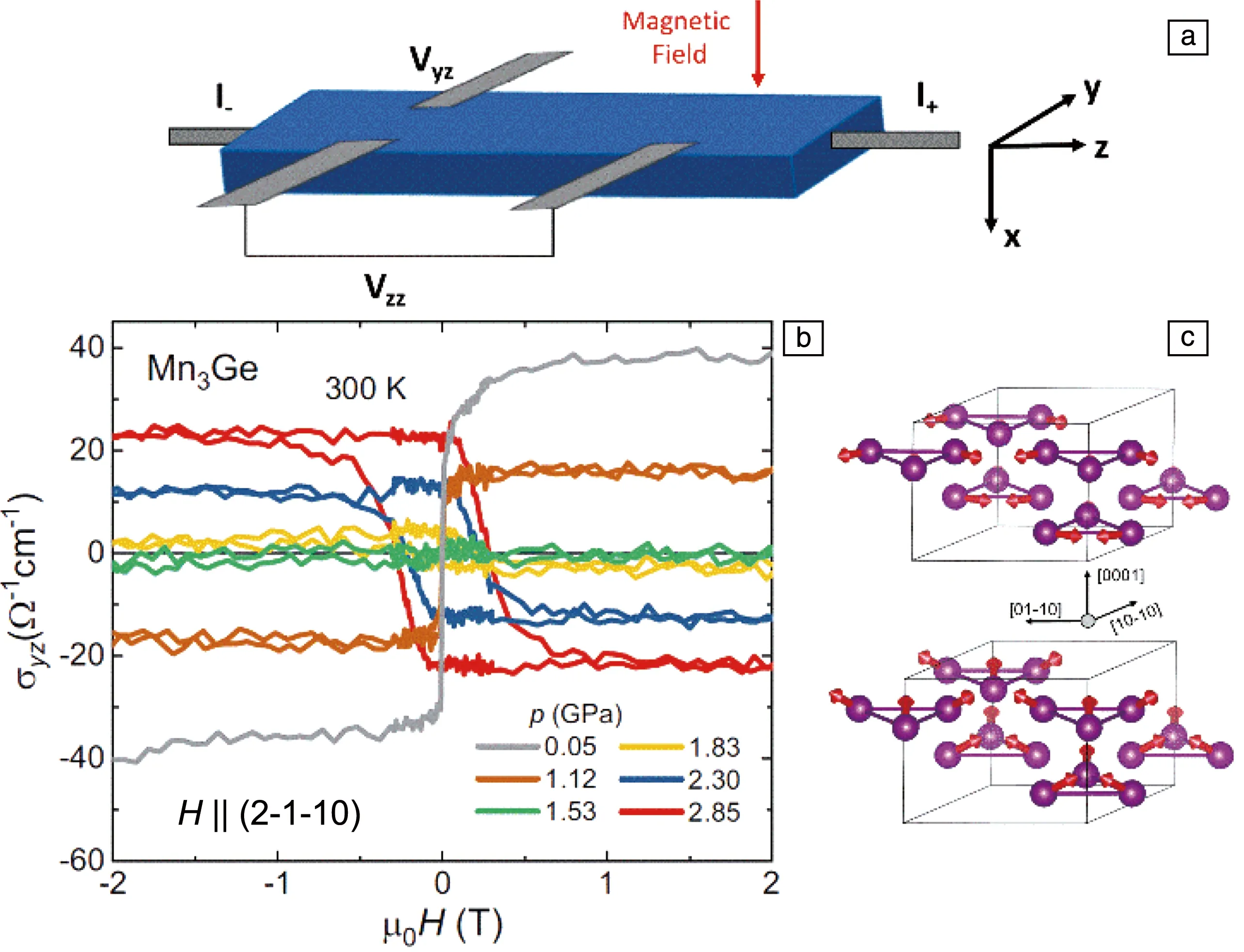
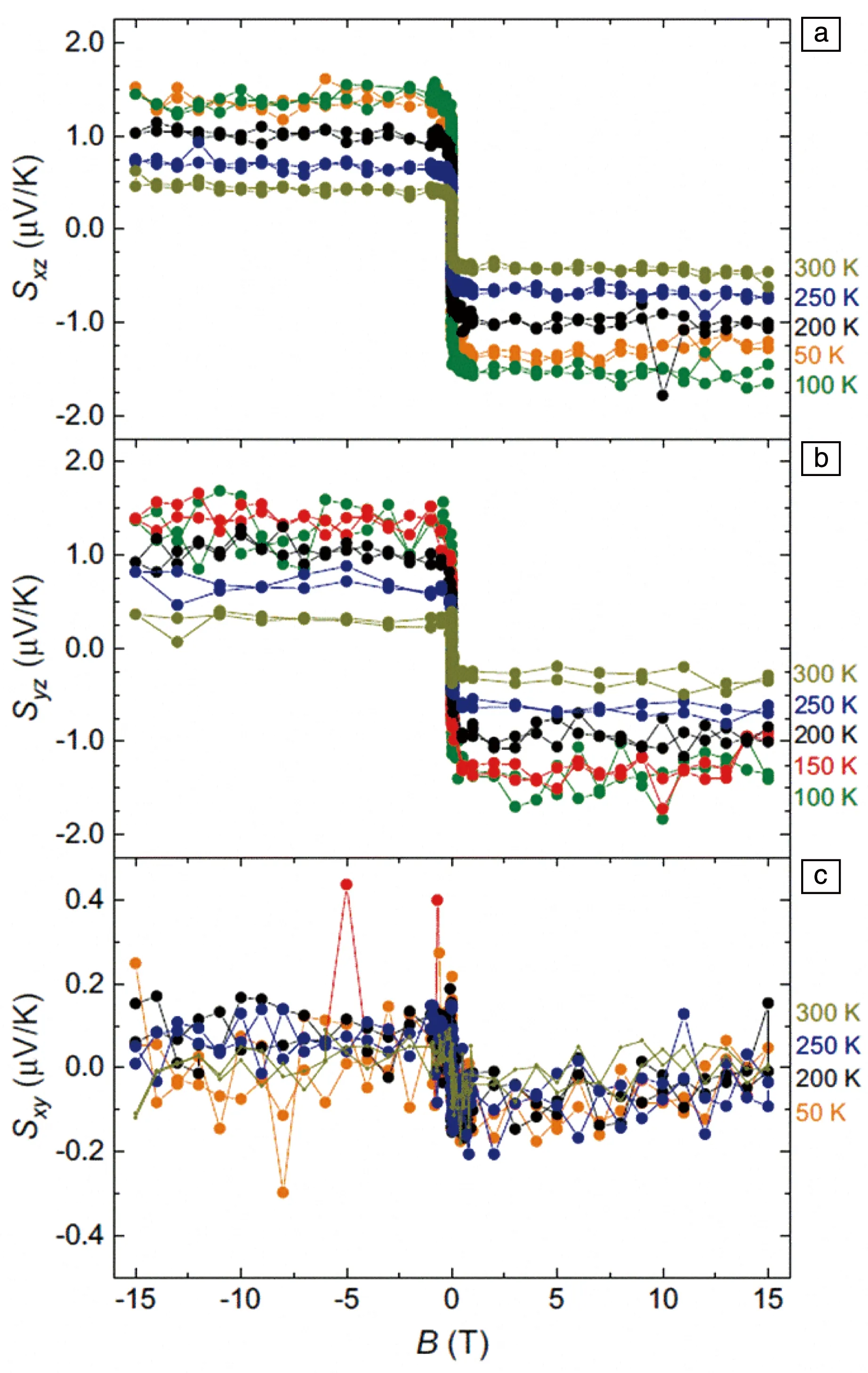
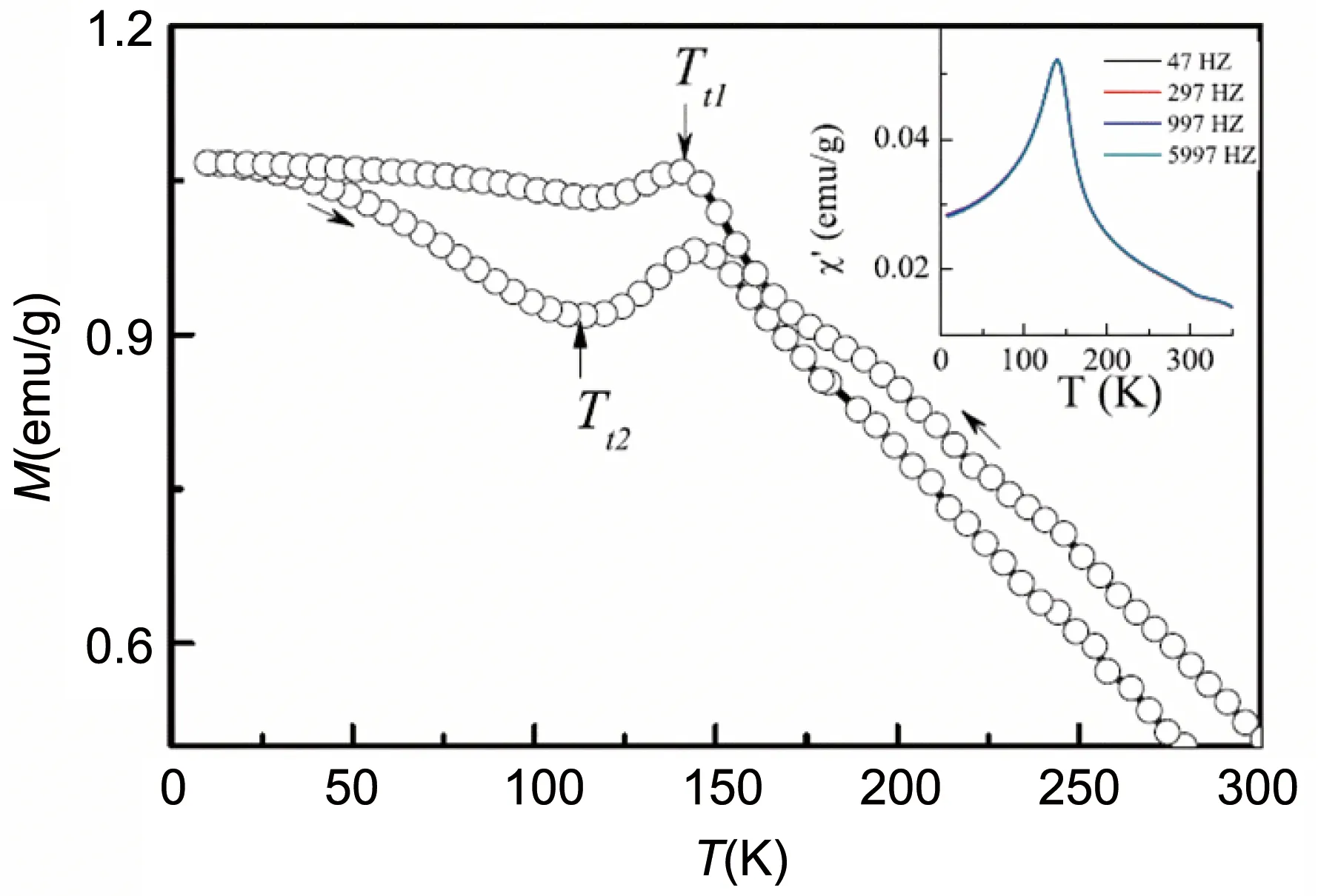
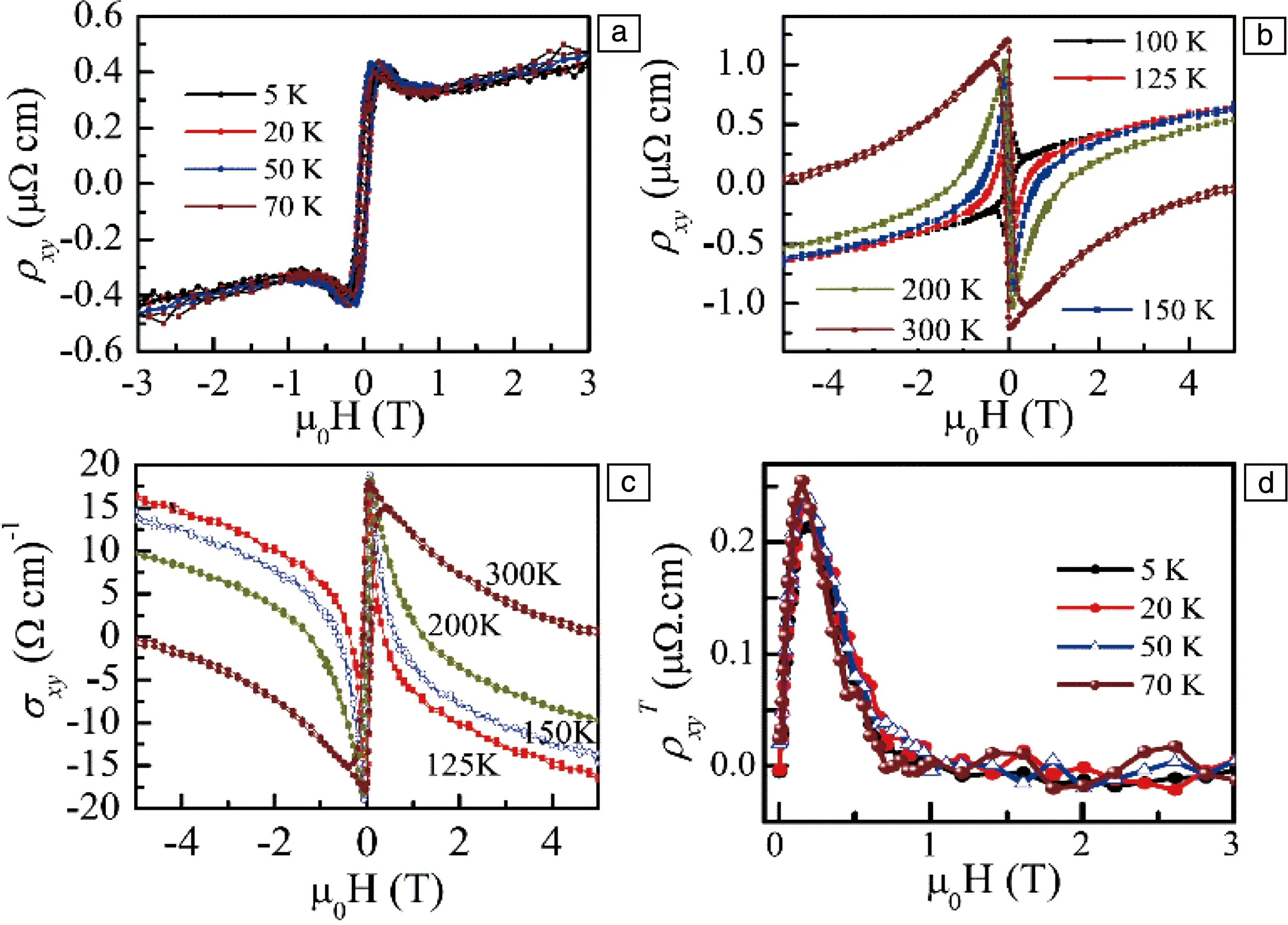
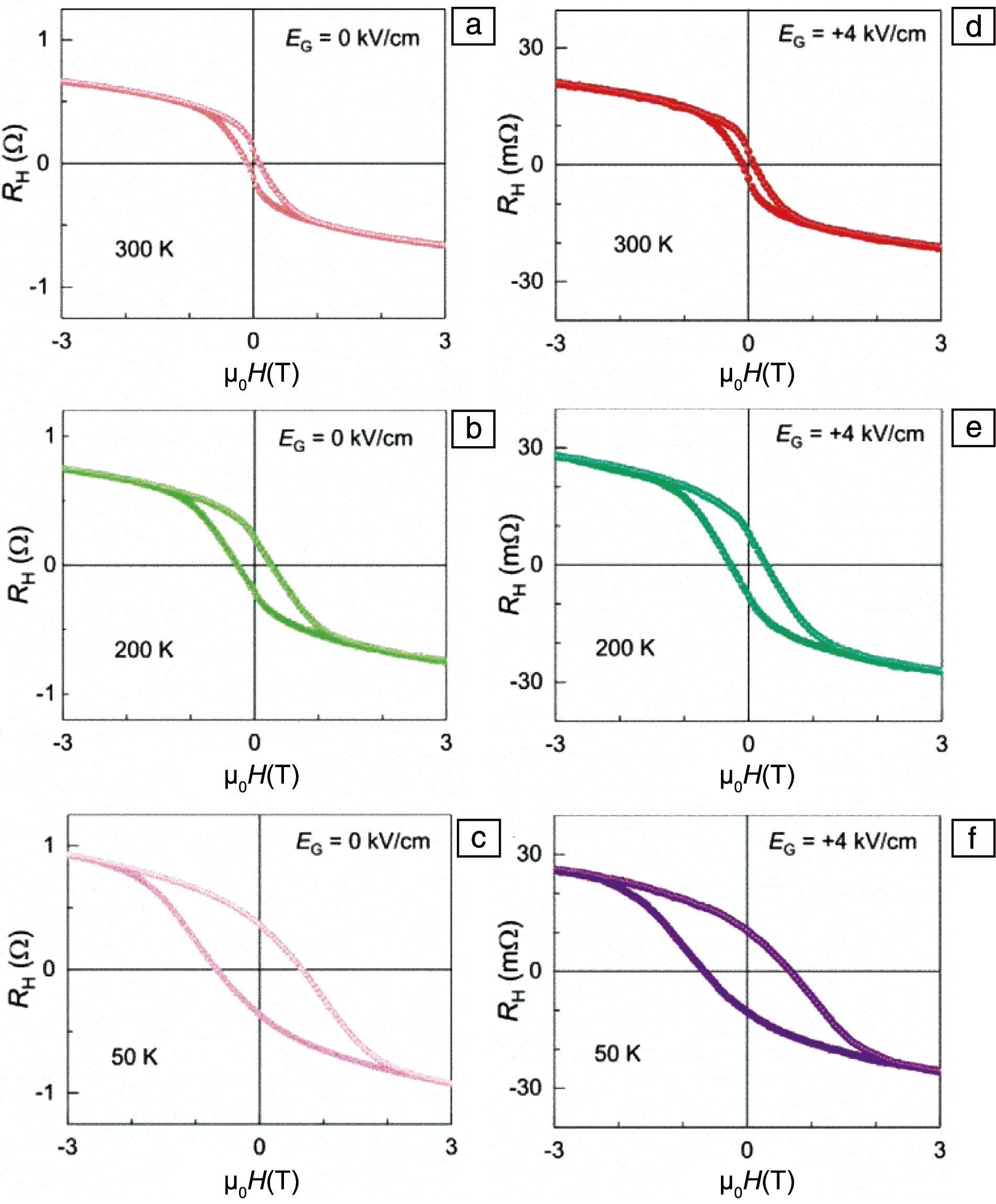
为了明确其磁转变所产生的不同磁结构,采用中子衍射测量之后分析发现Mn3Sn的磁相图可分为4个区域:① 10 在不同温度下对Mn3Sn的霍尔电阻率(ρH)进行测量发现,该曲线具有明显的磁滞(图5a)。当T=235 K时,|ρH|为2.5 μΩ·cm;当T=190 K时,ρH接近于0,且|ρH|随着外加磁场磁感应强度B的增加而线性增加。从ρH-B曲线中提取了零场(B=0 T)下的ρH来揭示AHE自发分量的温度依赖性(图5b),发现|ρH|在190 K温度以下几乎保持为0,在大约235 K时增加到最大值,然后随着温度的升高而降低。很明显,ρH的变化与温度导致的磁结构的变化密切相关。根据这一关系,可以通过改变Mn3Sn的磁性结构来调整其AHE。 图5 Mn3Sn不同温度下的霍尔电阻率随磁场的变化曲线(ρH-B曲线)(a),零场下霍尔电阻率的温度依赖性(b)[13]Fig.5 Field dependence of Hall resistivity ρH at different temperatures(a),temperature dependence of Hall resistivity at zero field(b)[13] 将拓扑学的概念引入到物理学中来描述随参数连续变化而保持不变的物理量时,能够解释很多关于磁输运方面的问题和现象[17, 18]。拓扑非平庸自旋结构的局部磁矩在几何阻挫或Dzylashinsky-Moriya相互作用(DMI)的驱动下发生空间变化,产生了一种不同类型的霍尔效应,即THE[19]。THE的起源可归因于非零的标量手性自旋Xijk=Si·(Sj×Sk),其中Si·(Sj×Sk)代表3个自旋矢量形成的立体角,打破了时间对称性,称为实空间的Berry曲率。由于同样具有120°非共线反铁磁结构的Fe1.3Sb已经被报道具有THE[20],Nayak等对Mn3Sn合金中的THE进行了研究[21]。 图6 Mn3Sn在不同温度下拓扑霍尔电阻率的磁场依赖性(a),不同霍尔效应贡献的相图(b)[21]Fig.6 Field dependence of topological Hall resistivity at different temperatures(a),phase diagram showing contribution from different Hall effects(b)[21] ANE是由热电流引起的自发横向电压降,与磁化强度成正比[22]。AHE由所有占据态能带的Berry曲率决定,而ANE是由EF处的Berry曲率决定的[23]。因此,能观察到大的AHE并不能保证观察到大的ANE。ANE的测量对于明确EF附近的Berry曲率和验证最近提出的Mn3Sn中Weyl点存在的可能性具有重要价值[9]。 Ikhlas等对单晶Mn3.06Sn0.94和Mn3.09Sn0.91的Nernst效应进行了研究[24]。结果表明,零磁场下Mn3.06Sn0.94的Nernst信号(横向热电势)-Szx在室温下为~0.35 μV·K-1(图7a),与室温下的FePd(0.468 μV·K-1)、L10-MnGa(-0.358 μV·K-1)等铁磁体的报道值相当[25];在200 K的温度下达到了~0.60 μV·K-1(图7b)。面内的Nernst信号表现出几乎没有各向异性的滞后现象,零场下展现的Nernst信号值与高场下的饱和Nernst信号几乎相同,表明单晶Mn3Sn中具有大的自发Nernst信号。但面外c轴分量在实验精度范围内测量值为0,表明在这个方向上没有自发Nernst效应。通过ANE与磁化强度M的对比发现(图7a),低场下-Szx和M的滞后几乎相互重叠。另外,在大于~100 G的磁场区域,ANE效应几乎保持不变,而M随着磁场的增加呈线性增加,表明正常的Nernst效应和传统的ANE的贡献可以忽略不计。在Mn3.09Sn0.91中也可以观察到类似的行为(图7b)。 与Mn3Sn相比,Mn3Ge在磁性和AHE方面有所不同,在Mn3Ge中测量得到的反常霍尔电导值比Mn3Sn中的高将近3倍。此外,Mn3Ge并不会展现出类似于Mn3Sn中的任何磁转变,为其AHE的稳定性提供了保障。 图8 计算中所采用的Mn3Ge的磁结构(a),第一布里渊区和动量依赖的反常霍尔电导(b)[26]Fig.8 The magnetic structure of Mn3Ge used in the calculation(a), first Brillouin zone and momentum-dependent AHC(b)[26] 接着,他们在实验上对预测的AHE进行了实验验证。当电流沿(0001)方向、磁场平行于(01-10)(这种测量方式称为构型1)时(图9a),ρH在2 K的温度下达到5.1 μΩ·cm的大饱和值,即使在室温下也展现出了1.8 μΩ·cm的饱和值。在霍尔电导率曲线σxz-μ0H中可以看到(图9b),反常霍尔电导在2 K的温度下具有~500 Ω-1·cm-1的较大的值,在室温下则为50 Ω-1·cm-1。为了进一步研究实验中的AHE是否具有理论预测的各向异性,测量了电流沿(01-10)方向、磁场平行于(2-1-10)方向(构型2)时的霍尔电阻率,如图9c所示。在这种测量方向下,ρH在2 K的温度下约为4.8 μΩ·cm,在室温下约为1.6 μΩ·cm,略小于构型1得到的值。图9d为构型2下的反常霍尔电导曲线,可以看到尽管在2 K的温度下构型2的σH(σyz)(约为150 Ω-1·cm-1)要小于构型1的σH(σxz),但在室温下具有与构型1相似的值。在这两种情况下,对于正(负)场,ρH为负(正)。第3种测量方式为电流沿着(2-1-10)方向、磁场平行于(0001)方向(图9e和9f),被称为构型3。在这种构型下,所有温度下的ρH和σH都具有比较小的值。此外,AHE的符号和前两种构型的符号相反,即相对于正(负)场,ρH为正(负)。 图9 电流和磁场沿不同方向(3种构型)下的霍尔电阻率(ρH)(a,c和e)和霍尔电导率(σH)(b,d和f)的磁场依赖性[26]Fig.9 Hall resistivity (ρH) (a, c and e) and Hall conductivity (σH) (b, d and f) as a function of magnetic field (H), for three different current and magnetic field configurations[26] 虽然在正常条件下Mn3Ge并不会展现出类似Mn3Sn中的磁转变,但是如果对Mn3Ge施加外部压力的话其磁结构会发生显著变化。研究表明,随着压力的增大,Mn3Ge的非共线三角磁结构逐渐变为均匀倾斜的非共线三角磁结构,当压力增大到5 GPa以上时变为共线铁磁结构[27]。由于Mn3Sn合金中磁结构的变化在很大程度上会影响其输运性能,因此可以通过施加不同的压力来改变Mn3Ge合金中的磁结构,从而进一步研究Mn3Ge的磁结构与AHE的关系。 Nicklas等测量了静水压力与AHE之间的关系[28],测量装置如图10a所示,电流平行于(0001)轴,磁场平行于(2-1-10)轴。研究发现,随着压力的增大,霍尔电导率σyz的饱和值先降低,当压力为1.53 GPa时完全消失;继续增大压力,σyz的饱和值反向并逐渐增大,如图10b所示。在2.85 GPa的压力下,Mn3Ge合金中Mn原子的磁矩会由图10c顶部的磁结构变化为底部的磁结构。可以看到压力会导致磁矩向面外倾斜,进而影响电子能带结构,从而导致Berry曲率的变化。 图10 压力元件内使用的电传输测量样品装置示意图(a),室温下施加不同压力的Mn3Ge的霍尔电导率(b),在环境压力(顶部)和压力为2.85 GPa(底部)下的Mn3Ge的反三角自旋结构(c)[28]Fig.10 Schematic drawing of the sample device for the electrical-transport measurements used inside the pressure cell(a),field dependence Hall conductivity for Mn3Ge at room temperature for selected pressures(b),the inverse triangular magnetic structure of Mn3Ge at ambient pressure(top)and P=2.85 GPa(bottom)(c)[28] 除了反常霍尔电导之外,理论预测在Mn3Ge中还可以获得高达1100(ћ/e) Ω-1·cm-1的自旋霍尔电导率[26]。在对Mn3Ge薄膜样品的研究中,在Permalloy/Mn3Ge表面发现了高达90.5 nm-2的自旋混合电导系数,并且Mn3Ge的自旋霍尔角是Pt的8倍左右[29]。 由于Mn3Sn的磁结构在T=50 K以下缺乏磁有序性,并且形成了玻璃态的磁基态,从而导致ANE消失[15]。而Mn3Ge的磁有序和反常输运性质通常持续到最低温度,与Mn3Sn形成鲜明对比。 Wuttke等对Mn3Ge单晶的Nernst效应进行了测量,如图11所示[30]。结果表明,Nernst信号Sxz不依赖于磁场,表现出反常的行为,在非常低的磁场下即表现出步进特征,并且在B>0.02 T时就已经达到了饱和值。Syz也表现出非常弱的场依赖性,如图11b所示。两种方向都显示出高达室温的特殊饱和行为,随着温度的逐渐降低,Nernst信号从0.4逐渐升高到1.5 μV·K-1。Sxy则显示出不同的行为,如图11c所示。在这种配置中,Nernst信号非常小,阶梯状的行为只是略微可见,并且显示出非常弱的温度依赖性。 图11 Mn3Ge单晶的Nernst信号测量曲线[30]Fig.11 Nernst signal of the Mn3Ge single crystals[30] 除了单晶Mn3Ge之外,Mn3Ge薄膜在室温下也展现出0.1 μV·K-1的反常Nernst信号,与铁磁性Fe薄膜的反常Nernst信号(0.4 μV·K-1)相当[29]。 在同样具有手性的非共线三角反铁磁Mn3Ga中依然存在大的AHE。不同的是Mn3Ga存在六角到正交的晶格畸变,原来的共面磁结构会向c轴转变,使得非共面磁结构产生,这就导致Mn3Ga中THE的出现[31]。 Mn3Ga在100 Oe磁场下的磁化强度会随温度的降低先增加(图12)[31],到140 K左右出现一个磁转变,并且升降温曲线在此处展现出很明显的热滞,此处即为六角结构到正交结构的轻微畸变[32]。变频交流磁化率的测量表明这个转变没有频率依赖(图12插图),和结构变化相对应。 图12 Mn3Ga在100 Oe磁场下的热磁曲线,插图为不同频率的交流磁化率实部随温度的变化关系[31]Fig.12 M-T curves measured at 100 Oe field for Mn3Ga, the inset is temperature dependence of the real part of AC susceptibility measured at different frequencies[31] 图13 不同温度下六角Mn3Ga的AHE(a~c)和THE(d)[31]Fig.13 Anomalous Hall effect (a~c) and topological Hall effect (d) of hexagonal Mn3Ga at different temperatures[31] 室温反铁磁自旋电子器件的主要瓶颈之一是反铁磁材料中有限的各向异性磁电阻导致的小信号读出。这可以通过在非共线反铁磁物质中利用Berry曲率诱导的反常霍尔电阻或者基于反铁磁自旋的有效操纵建立磁隧道结器件来克服。因此,刘知琪团队在300 ℃的溅射温度下在(100)取向的铁电0.7PbMg1/3Nb2/3O3-0.3PbTiO3(PMN-PT)单晶衬底上生长了50 nm厚的Mn3Ga薄膜,并通过压电应变调制对反常霍尔电阻进行了研究[35]。 研究结果表明,在50~300 K的温度范围内,随着温度的降低,零磁场下的霍尔电阻从~0.112 Ω增加到~0.364 Ω,用于切换反常霍尔电阻的矫顽场从93 mT显著增加到667.6 mT(图14a~14c)。由于静电调制机制对50 nm厚的Mn3Ga金属薄膜几乎不起作用,因此通过在PMN-PT衬底上垂直施加4 kV·cm-1的栅极电场EG,分析了压电应变对AHE的影响,如图14d~14f所示。可以看到EG=4 kV·cm-1的AHE在所有温度下都表现出巨大的变化。例如在50 K的温度下,零场的霍尔电阻从EG=0 kV·cm-1时的~0.364 Ω变化到了EG=4 kV·cm-1时的~0.010 Ω。由于非共线反铁磁体中的AHE是其自旋结构的敏感探针,压电应变下AHE的巨大变化表明其自旋结构在应变调控下发生了巨大的变化。 图14 在300 K(a)、200 K(b)和50 K(c)的温度下,EG=0 kV·cm-1时Mn3Ga/PMN-PT异质结构的反常霍尔电阻;在300 K(d)、200 K(e)和50 K(f)的温度下,EG=4 kV·cm-1时Mn3Ga/PMN-PT异质结构的反常霍尔电阻[35]Fig.14 Magnetic-field-dependent anomalous Hall resistance of the Mn3Ga/PMN-PT heterostructure at EG=0 kV·cm-1 at 300 K(a),200 K(b) and 50 K(c);magnetic-field-dependent anomalous Hall resistance of the Mn3Ga/PMN-PT heterostructure at EG=4 kV·cm-1 at 300 K(d),200 K(e) and 50 K(f)[35] 自旋泵浦效应是产生自旋流的重要方法,进一步利用逆自旋霍尔效应(ISHE),可以将自旋流转化为可探测的电荷信号,从而实现自旋泵浦的电测量。因此,自旋泵浦效应结合ISHE成为研究各种材料中自旋-电荷转换的经典手段。 Singh等对室温下多晶Mn3Ga/CoFeB异质结中的ISHE和自旋泵浦效应进行了系统的研究[36]。实验中通过对ISHE进行不同角度的测量来分解各种自旋整流效应。最终得到的自旋混合电导系数、自旋霍尔角和自旋霍尔电导率的值分别为(5.0±1.8)×1018m-2、0.31±0.01和7.5×105(ћ/2e) Ω-1·m-1。如此高的自旋霍尔角和自旋霍尔电导率使得Mn3Ga在未来的自旋电子器件中具有很好的应用前景。 本文对具有非共线反铁磁的DO19型六角Mn3Z(Z=Ga,Ge,Sn)合金的磁性和输运性质进行了综述。发现通过理论计算对Mn3Z合金的输运性质进行预测之后,在实验上都得到了验证,并观察到了非常优异的物理性能。这表明通过理论计算能带结构,调控和发现EF附近具有Weyl点的材料,从而寻找输运性能优异的材料是可行的。当前对Mn3Z(Z=Ga,Ge,Sn)合金的报道已经提供了明确的经验框架,为后期及进一步制作具备优良性能的非共线反铁磁材料打下了坚实的基础。因此,还需要大量的理论计算及实验以进一步指导六角反铁磁材料输运性能的有效调控。另外,通过对其他材料体系的研究发现,适当的无序掺杂会明显提高材料拓扑能带引起的Berry曲率,进而提升其输运性能,这为将来进一步提升六角反铁磁Mn3Z(Z=Ga,Ge,Sn)合金的性能提供了重要思路。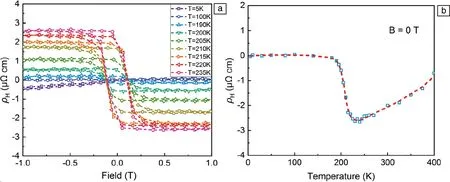
2.2 Mn3Sn中的THE
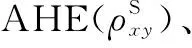
2.3 Mn3Sn中的ANE
3 六角Mn3Ge合金的输运性质
3.1 Mn3Ge单晶中的AHE
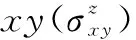
3.2 Mn3Ge中的ANE
4 六角Mn3Ga合金的输运性质
4.1 Mn3Ga中的AHE到THE的转变
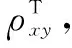
4.2 Mn3Ga/PMN-PT中的AHE
4.3 Mn3Ga薄膜中的逆自旋霍尔效应和自旋泵浦
5 结 语

