水工建筑物初生空化数及其比尺效应研究进展

郑雪玉,吴时强,杨家修

(1.中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550081；2.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072；3.南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏 南京 210029)

空化空蚀现象于1893年最先在军用驱逐舰和汽轮机螺旋桨中发现，30年后在水电水利工程的高水头泄水建筑物中出现。直到现在水工建筑物中空化空蚀问题时有发生，并且严重危害泄水建筑物的安全运行。有许多专著和论文对水工建筑物的空化空蚀及掺气减蚀技术问题进行了专门叙述并收集大量实例[1-2]。国内比较典型的破坏案例有：刘家峡泄洪洞反弧段及下游底板空蚀破坏；龙羊峡泄洪洞左右边墙严重空蚀破坏；丰满水电站溢流坝面的空蚀破坏；盐锅峡溢流坝导流孔空蚀破坏；丹江口导流底孔出口空蚀破坏；柘溪溢流坝挑流鼻坎空蚀破坏等。水工建筑物的空化空蚀问题严重威胁工程的安全运行，加深对初生空化数的研究，按照不同水工建筑物结构部位研究其初生空化数，并深入分析其比尺效应，能在设计阶段对规范规定的防空蚀设计做到精确响应，极大保障结构安全，从根源上减免空化空蚀。季斌等[3-5]针对空化水动力学非定常特性、空化机理以及减免空化的掺气减蚀技术等方面的进展及尚存在的问题进行了全面论述。本文在此基础上从初生空化数计算公式、初生空化数的比尺效应及水工建筑物不同部位的初生空化数研究情况三方面进行综述。

1 初生空化数计算公式

空化的本质现象是由于最小压强pmin小于液体饱和蒸汽压强pv，气核界面处的液体相变成蒸汽，使气体急剧膨胀而成空泡。但流场中的气核微小多变，具体参数难以测定，所以无法用这些量判断水流空化与否。那么通过研究可采用初生空化数来判断空化与否。好比雷诺数用来判断层流和紊流，弗劳德数用来判断急流和缓流。而初生空化数则是水流是否发生空化现象的判断标准，若水流空化数小于对应的初生空化数，则为空化流，反之，则为非空化流。空化数还有另外两方面的意义[6]：①描述设备对空化破坏的抵抗能力；②衡量不同流场空化现象的相似性。关于初生空化数具体计算方式，国内外已有不少研究，但各家得出的结果不尽相同，本文对部分初生空化数公式汇总对比见表1。

表1 初生空化数公式对比

表1各公式不尽相同，分析认为一方面由于具体研究对象的边界条件、结构形式、运行条件等不同，及所考虑的影响因素及权重不同所致；另一方面则是由于试验条件、测量方法、分析方法差异所致。但公式也呈现出了一定的共性，比如大部分衍生公式都是在经典Thomas定义式基础上，加入影响因子及权重而得。除此之外，Roger[14]针对圆盘绕流进行研究，认为其具有较大的分离区，雷诺数影响最小压力系数，从而影响空化初生，建立了适用于汽型空化的圆盘绕流初生空化数计算公式。Roger等[15]还研究了水质对尾涡流初生空化的影响，给出相应公式。黄建波[16-17]建立的公式表明几何相似的两系统中，初生空化数只与最小时均压力系数及脉动压力强度有关；还提出从失稳气核与液体的体积比、单位时间内的失稳气核个数两种比较直观的方式定义空化初生现象和初生空化数。夏洪维[9-10]建立了考虑水流和水质效应的初生空化数公式。Zhang等[18]建立了初生空化数与雷诺数的关系。倪汉根对初生空化数有着多方面研究，不仅建立了凹槽中的旋涡初生空化数计算公式[12]，还对弓形凸体和孔板泄洪洞[1，19]进行了概率估计及直观表达式的计算，并将结果与实测初生空化数进行对比，3种结果相当接近，且与实测值差别不大。

从表1初生空化数公式发表年份来看，早期相关研究较多，主要集中于20世纪八九十年代，到21世纪以后，研究成果相对较少。针对已有成果无论从哪类因素出发建立的新初生空化数公式，都是基于经典公式。该式更具普适性，形式简单，适用性较强。然而，经典公式只能提供初步参考，仅考虑了液体的饱和蒸汽压强，未计入影响初生空化的其他因素。在实际工程中，还应根据具体工程特点，通过模型试验对经验值进行修正。

2 初生空化数的比尺效应

空化现象本身相当复杂，到目前为止，要准确预报水工建筑物的初生空化仍然存在一些问题，众多学者研究发现：初生空化数存在比尺效应或尺度效应，即所谓的“空化数偏离”[20]。

目前对空化的研究手段主要还是采用物理模型试验。模型与原型之间必然存在比尺效应[21]，故把模型上测的初生空化数直接应用于原型是不合理的，也是不安全的。为了较好反应原型初生空化数，必须对模型所测结果进行比尺效应修正。国内外学者进行了大量研究，代表成果有Keller等[22-28]、任静等[29]、倪汉根[30]、夏维洪[10,31]、潘森森等[20]修正公式。

2.1 Keller等[22-28]公式

Keller博士用自己发明的“涡流腔抗拉强度仪”测量，在大量试验研究的基础上，综合考虑几何尺度、速度、紊流度和水质条件等各种因素，将修正关系合并成一个公式：

式中：L、ν、v、S分别为模型特征长度、介质动力黏性系数、来流速度和来流紊流度；L0、ν0、v0、S0分别为L、ν、v、S的参考值；K为试件形状和空化类型特征；v0为一个几乎稳定的常数，一般取12 m/s。该式主要以不同线型的轴对称头体和不同剖面的水翼试验结果为依据。他还在考虑了水流阻力以及流速和绕流体试件尺寸对空化数影响时得出如下关系式：

(2)

Keller提出的修正公式是经验推导的，是有量纲的。流速比尺效应Cw引用的是经验参数，给它一个速度量纲，在物理意义上还没有做出解释。该式基本来源于有限数据的经验总结归纳，一旦试验装置和测试条件不同，就会产生偏差，在一定范围内可能适用，但不能推广，要按无量纲数来归纳比尺效应才是最可靠的。

2.2 任静等[29]公式

综合考虑水质影响因素，在安东和普列达提出的水轮机组相似率基础上，得到比较全面的电站水力机械的空化比尺效应公式：

(3)

式中：σ为空化数；R为转轮叶片上最低压力点的半径；Δh为转轮叶片上最低压力点到水轮机出口的水力损失；H为工作水头；α为水中空气的相对体积含量；τ为水的表面张力；γ水的表面张力；下标H和m分别表示原型和模型值。该式可在已知模型空化系数的前提下，通过计算比较精确地确定原型空化数。

2.3 倪汉根[30]公式

倪汉根对空化问题研究较多，提出的空化数比尺效应公式为

(4)

(5)

式中：-CPmin为最小压力系数；λL为模型的长度比尺；σc为气核失稳的临界空化数；Rc为气核失稳的临界半径。应用碧口水库孔板洞系列减压模型试验对该进行了验证，基本上反映了减压试验中原型和模型初生空化数的关系。但也做了一些假定，因此其要求最好满足v>5.0 m/s，否则因修正值占比很大，预报的原型初生空化可靠性不高。

他还提出含沙水流中初生空化数的表达式[1]：

(6)

式中：ξ为用v表示的从参考点到点之间的水头损失系数；w为在Pmin处沙粒与液体的相对速度；β为反映与气核生长过程有关的惯性、溶解气体扩散等影响的一个因子；β为时均压强和脉动压强均方根的峰值系数。式(6)为讨论含沙水流中的各种因素(如阻力损失系数、沙粒与液体相对运动、黏性变化变化、表面张力变化、密度影响、空化核数量变化)对初生空化数的影响提供了基础。

2.4 长江科学院[31] 公式

长江科学院总结了5种泄水管的类型，推导出短泄水管末端的空化数为

(7)

式中：D2为进口曲线与管道直线交界断面处的直径；C为与泄水管形式有关的常数；ha为大气压；hv为水的饱和蒸气压；Re为雷诺数。

式(7)说明空化数与雷诺数相关，当雷诺数足够大时，σ可接近常值。模型试验表明，只有模型雷诺数Rem>106时，才有可能接近自动模型区。为此原型和模型的特征线性比尺应该为Lr<10-4(ReH)2/3。

2.5 潘森森[20] 公式

潘森森给出了形式上较完整的空化数表达式：

(8)

潘森森说明空化的内涵是式中右边第1项低压条件和第2项介质影响，他们是构成新空化相似参数的基本项。由水动力学因素引起的空化比尺效应是式中第3项低压因系，第4项是时间因素对σ数的修正，即由泡动力学因素引起的空化比尺效应，第3、4两项可以不包含在上式对空化数的定义中，属于空化数的外延，可称为空化的比尺效应修正。

上述各家从不同角度计及空化比尺效应的影响因素，当然也包括空化概念的定义范畴及空化数的定义等问题的讨论，他们重点找出空化数定义中的缺陷、修订并补充完整，以寻求空化数与空化现象偏离的解决途径。这些因素主要包括流体黏性、紊动、表面张力、气核含量或抗拉强度等介质条件，归结为模型的“尺度效应”和“速度效应”等等。从各家表述的修正理念与检验结果来看，也不尽如人意。这就表明，仍有某些未计的重要影响因素存在。

3 水工建筑物不同结构的初生空化数

3.1 过流表面平整度

过流表面不平整度通常分为均布不平整糙面和孤立不平整凸体，比较容易引起空化与空蚀的是孤立不平整凸体。国内外学者针对不平整凸体初生空化数研究较多。Colgate[32]通过研究指出混凝土表面不平整引起的空化初生与均布糙体的当量高度和边界层厚度的比值密切相关。Numachi等[33]验证了Colgate的观点。Arndt 等[34-35]指出空化初生都起源于紊流压力脉动，且跟边界层内的剪切力密切相关，得出初生空化数公式为

σi=16Cf

(9)

式中：vo、τo分别为均匀流速度和板面剪应力。

倪汉根[19]在以上基础上，从工程实用角度出发，给出了下式:

(10)

式中：R为水力半径；n为糙率；g为重力加速度。

Holl[36]在σi=-Cprm假设下，得到：

(11)

式中：Δ为不平整凸体高度；uΔ为未受扰动流速场中与凸体最高点处相应的流速；δ、δ*、θ分别为边界层厚度、位移厚度和动量厚度。

1979年，Arndt等[38]提出了比较带有普遍实用性的经验公式：

(12)

式中：c、a、b均为根据试验数据定出的常数系数，他们与孤立不平整凸体的形状有关，需由减压试验确定。该式是在综合了当时能收集到的孤立不平整凸体的全部实测资料，重新归纳并整理后得出的。

Holl等[39]随后研究了压力梯度对光滑平板上孤立不平整凸体初生空化数的影响，在式(12)中增加了一个反映压力梯度的修正项，提出：

(13)

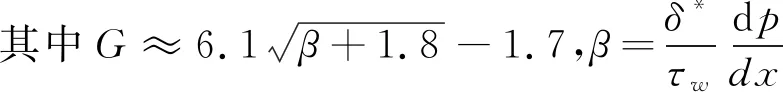
式中：G为与压力梯度有关的形状参数因子，但一般情况下(如溢流坝面和泄洪洞)，压力梯度不太大，对a的影响也较小，可忽略不计；d为常系数。

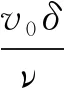
周胜等[40]指出各种接近流线型突体的初生空化数近似等于最小压力系数，针对多种接近流线型突体的最小压力系数应用有限元法按照势流分析进行了计算，计算成果和试验成果比较一致，但该计算分析中未考虑黏性的影响。

梁川等[41]通过试验拟合，给出50 m/s流速级时三角形凸体初生空化数为

(14)

式中：vΔ为突体顶点处的流速；Pmax为近壁空泡溃灭压强；vΔ为突体点处流速。该研究成果为后续进行不平整度控制标准提供了相应依据。

3.2 闸门及门槽

水流流经门槽，流态复杂，若出现空化，会对闸门正常运行造成严重影响。对于门槽的初生空化数，首先是苏联学者的试验研究，但其成果提出的公式较复杂，不便于工程设计人员参考应用。DL 5039—1995《水利水电工程钢闸门设计规范》推荐了Ⅰ型、Ⅱ型钢闸门的体型参数和适用范围，还对应给出了初生空化数的经验公式，该规范中给出的相关内容对于设计人员应用简单方便。宋昉[42]研究了门槽空化的相关问题，指出门槽发生空化现象的部位先后是门槽下游方角、导轨顶面、侧轨顶面、进口闸墩弧面。他提出影响门槽空化的几何参数宽深比和错距比是最主要的，该观点与SL 74—2013《水利水电工程钢闸门设计规范》一致。黄荣彬等[43]研究了斜交门槽初生空化数，表明门槽初生空化数随斜角β的增大而增大，同时也随宽深比(W/D)的增大而增大。其拟合关系为

(15)

该研究同时指出，除了宽深比和错距比以外，斜坡比及圆角比也很大程度上影响这门槽初生空化。

3.3 孔板及洞塞

孔板和洞塞主要用作高水头大直径泄洪洞内消能，小浪底水利枢纽中首次成功应用孔板进行消能，美国Glen Canyon坝首先成功采用洞塞消能，二者的成功消能经验都具有很高的参考价值。但孔板和洞塞消能的同时很容易出现空化空蚀问题。孔板和洞塞的初生空化数计算尤为重要，Ball[44]将其表示为

(16)

式中：HT为孔板上游总水头；H2为在孔板下游选择的参考点压强水头；Hv为与水温相应的相对饱和蒸汽压强水头。

Tullis[45]将孔板和洞塞的初生空化数表示为：

(17)

式中：pu和pd分别为孔板上游和下游1倍管径处的压强；pv为与水温相应的饱和蒸气压。

李中义等[46]认为孔板初生空化数主要取决于孔板的体型，同一孔径比的孔板，阻力系数越大，消能率越高，孔板后的紊动也越强烈，因而也就越容易空化。对同一阻力系数的孔板，孔径比越大，要求孔口顶部越尖，也就越容易发生空化。因此，初生空化数是孔径比和阻力系数的函数。

徐福生等[47]提出了初生空化数随着孔径比的变化而变化。各级孔板的初生空化与消能率成反比，设计中要平衡孔板初生空化与消能率之间的关系。

倪汉根[48]还提出了新的公式：

(18)

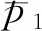
Hamittan[49]洞塞的初生空化数公式为

(19)

式中:p0为洞塞喉管中部压强；p2为洞塞喉管突扩约6.5Dt处压强；Dt为隧洞内直径；vpl为洞塞过流断面平均流速；Apl为洞塞中各过流通道的面积之和；At为隧洞过流面积。分析可知洞塞的初生空化数不仅和Apl/At有关，还和洞塞中过流通道的布置方式有关。倪汉根等[1]还对孔板和洞塞的消能方式进行了简单比较，分析可知孔板的消能效果不如洞塞好。

3.4 有压弯曲管道

在水利工程中，常采用纵轴弯曲的管道。有位于水平面内的，也有位于铅直面内的；断面有圆形的，也有矩形的；管道中的水有直接流入大气的，也有流入尾水渠的。关于有压弯曲管道的初生空化数，倪汉根等[1]总结了若干水利枢纽中有压弯曲管道的主要几何特性及相应水流空化数与初生空化数，各枢纽有压管道的初生空化数大部分在0.3～0.65范围内，在前人的研究，总结出有压矩形断面弯管的初生空化数修正公式：

(20)

式中：Rr为弯管相对曲率半径；D为管道直径。该式建立了初生空化数与弯管曲率半径的直接关系，同时考虑了脉动压力的影响。

倪汉根等[1]还建立了光滑有压圆形断面弯管中的初生空化数估算式：

(21)

式中：p0为弯管上游直管段中的时均压强；k1、k2分别为离心压强的变化系数与极限系数。但该式估计的结果远低于试验值，考虑因素不够全面，还需进一步研究。

Tullis[45]通过研究，建议弯度为90°，曲率半径为1.5的圆形断面弯管初生空化数经验式为

σi=7.80D0.46

(22)

该式能较好地估算该种弯管的初生空化数，研究表明圆形断面弯管的初生空化数远高于矩形断面弯管[50]。

另外关于堰面的初生空化数控制，我国SL 253—2018和DL/T 5166—2002《溢洪道设计规范》中均对WES实用堰规定了最大负压值，堰面初生空化数的控制准则主要是不平整体，可参照平整凸体初生空化数计算公式。

4 研究展望

长期以来，空化空蚀问题一直威胁着水工建筑物的安全运行，影响着设计人员结构设计的合理性，规范上明确指出对于流速接近15 m/s的过水建筑物要慎重选择体型，对于流速超过20 m/s的区域要重视，此规定充分说明空化空蚀问题是水电工程中的重要难题，目前针对该问题已有大量研究成果，尤其针对某些具体工程问题，也进行了相应研究。然而，由于水工建筑物各种特有的复杂水流现象基本上都是发生在细观尺度，大多具有微观、瞬时、随机、多相的特性，目前不少相关研究成果还不能令人满意。概括来讲，今后还应进一步加强以下几个方面的研究：

a. 空化空蚀机理的研究还不甚充分，应进一步探索空化空蚀问题的微观动力学机制。根据我国“十三五”水利发展规划预测2050年全球水电装机容量将达20.5亿kW，面对目前全球水电工程迅速发展之势，研究复杂多变环境下的水工建筑物不同结构部位的空化空蚀微观机理，从微观角度保障结构安全尤为重要。

b. 应重视水工建筑物水流空化空蚀的合理数值模拟。目前虽然也有较为可靠的空化模型，但是多用于精细网格、模拟时间较短的问题中，如水轮机空化等。对于较大体型的水工建筑物难以实现，其仍然以空化数作为空化判断标准。因此对于空化的数值模拟，应合理选取关键方程及初始条件，实现对水工建筑物各结构空化空蚀问题的合理数值模拟。

c. 重视具体水工建筑物不同结构空化空蚀问题控制标准及相关规范研究。目前SL 253—2018《溢洪道设计规范》给出了闸墩墩头、闸门槽、堰面局部变坡、泄槽不平整度、挑流鼻坎分流墩、消力池内消力墩规定了部分体型及初生空化数，而DL/T 5166—2002《溢洪道设计规范》则仅以空化数和流速来规定。鉴于目前水工建筑物结构体型多变，且控制标准较笼统，应具体按照结构部位对已有体型进行相应初生空化数规定。