基于动态神经网络的水泥熟料堆积体建模方法
闻 岩,黄泊霖,袁 林,刘浩然,鞠艳旭
(1.燕山大学机械工程学院,秦皇岛 066004;2.燕山大学信息科学与工程学院,秦皇岛 066004)
0 引 言
颗粒物质广泛存在于制药、水泥、化工等工业生产中。但是涉及颗粒运动行为时,许多基本问题还没有弄清楚。颗粒聚集体流动时表现出类似流体的运动行为,但是使用流体力学理论对其描述并不合适,究其原因在于颗粒体系复杂的力链网络。力链网络不仅支撑着颗粒体系的部分重量还能承担一定的外载荷,其在颗粒接触时开始出现,并随着颗粒流动不断演变[1]。研究颗粒动力学问题首先需要建立静力学模型,对基于数值模拟的颗粒流动研究而言,建立颗粒体系初始堆积状态的离散元模型十分必要。为了建立能够反映颗粒接触关系的聚集体模型,国内外学者在建模方法上展开了一系列的研究。在单颗粒方面,Nolan等[2]提出了利用数个球体的包络面逼近特定颗粒轮廓的单颗粒建模方法。对于特定颗粒的轮廓特征,多数研究者先通过扫描技术获取颗粒的外形特征,再利用较小粒度的颗粒球对其填充[3-5]。以上研究都着眼于对单个颗粒建立精准模型。但是有关复杂颗粒体系建模的研究还比较少。在体系内部通常包含大量颗粒物质,粒度分布存在一定范围,并且各个颗粒间又存在着相互作用。为了对特定颗粒群展开研究,所建立的离散元模型应考虑体系内颗粒的真实接触情况,应尽可能与真实的颗粒模型等价[6-8]。
水泥熟料是比较典型的颗粒物质,熟料堆积体在生产中因受推动棒作用而往复运动,为了利用离散元软件研究水泥熟料的运动行为,就需要先建立堆积状态下的离散元模型,但是关于水泥熟料堆积体建模的报道较少。其中,张文明等[9]先利用双目视觉技术重建熟料层,再通过网格划分技术还原熟料几何外形,实现了水泥熟料颗粒体系的建模。但是并非以力链形成为线索。
本文提出一种基于神经网络的颗粒体系建模方法。首先通过试验获取颗粒的粒度与质心三维坐标信息,使用神经网络建立一个预测模型,以颗粒粒度分布及质心三维坐标作为模型的输入,以颗粒质心三维坐标作为输出,训练神经网络并利用自相关函数和互相关函数验证网络。预测模型只需输入颗粒集合的粒度分布,网络就可以预测出各个颗粒的质心三维坐标,进而实现对颗粒堆积体的建模。这种建模方法可以推广到其他颗粒物质。
1 模型重建方法
高温环境中的水泥熟料在工业生产时易受到风室中冷空气的影响而突然冷却,变为半熔融状态,随后在凝结破裂后不断堆积,最终聚集成一定数量的颗粒集合,即颗粒堆积体[10]。这个过程中不规则的熟料因边角钝化,近似成球体。本文在进行处理时亦将颗粒等效成球体。熟料堆积体内部含有大量形状各异的孔隙结构,常称其为多孔介质。此类结构可以采用切片法、立体成像法和图像法进行三维重建[11]。
本文拟采用切片法对熟料堆积体进行三维重建,以期获取颗粒集合中各个颗粒的粒度值和质心三维坐标信息。研究方法如图1所示,以工业生产的水泥熟料为试验样本构建堆积体,制作切片并采集图像。通过图像及数据处理过程,获取包含颗粒三维坐标及粒度值的空间信息。将空间信息进行归一化处理,利用动态神经网络建立预测模型并对网络进行训练,训练完成后对网络进行验证。
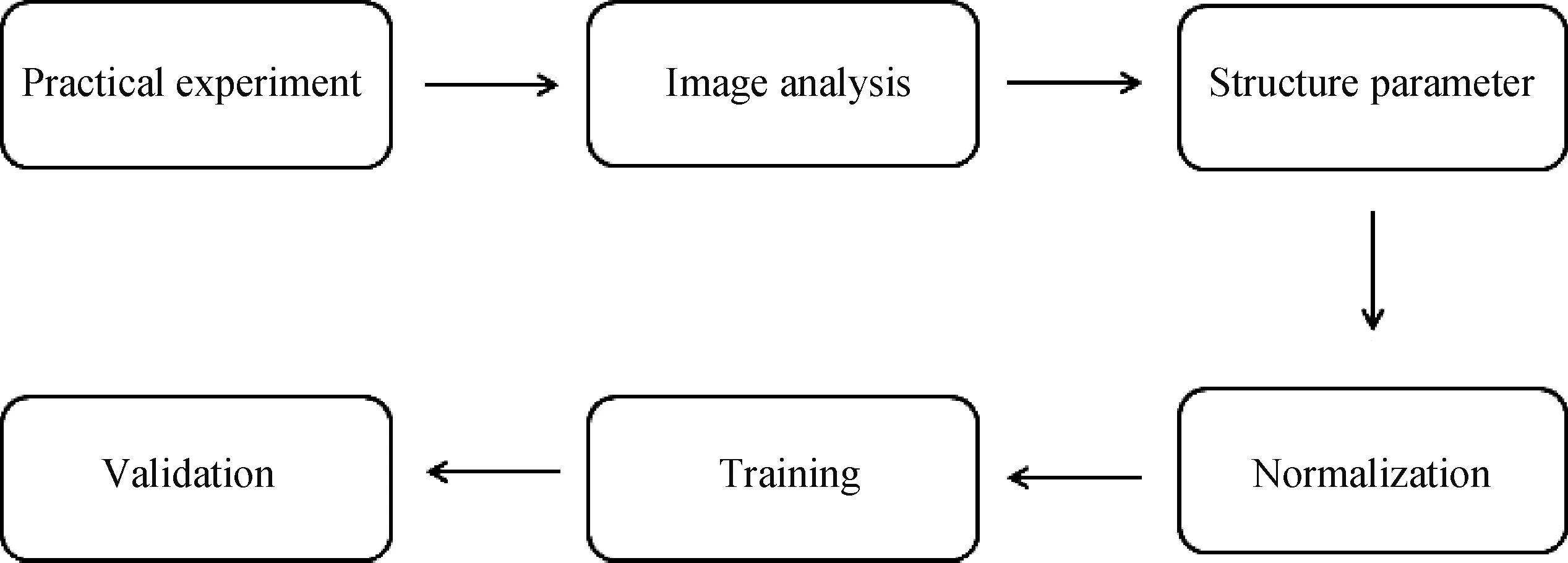
图1 研究方法Fig.1 Research method
2 试验方法及数据处理
为了获取相关数据,试验时以工业生产的水泥熟料为试验材料,模拟熟料在篦冷机内的堆积过程。
首先选取样本颗粒,考虑到在堆积过程中会出现边壁效应,即颗粒与硬边界直接接触而导致的对堆积成型效果的影响,试验中在盒体内壁附着一层厚达20 mm的保温棉,承载熟料-石膏混合体容器软边壁的边长为150 mm,料盒硬边界总体尺寸达到190 mm。使用样本颗粒密实填充总体尺寸为190 mm的无盖立方体料盒,使用石膏浸渍剂固化颗粒堆积体,固化后的堆积体如图2所示。因为颗粒粒度分布绝大部分在20~60 mm之间,在试验操作中,首先沿固化熟料体Z轴方向,使用切割机按20 mm等距切割堆积体,然后用相机采集切片图像并编号,切片图像如图3所示。其中乳白色部分为浸渍剂,黑色部分为水泥熟料。
在数据处理之前,先对所采集的图像进行预处理。利用ImageJ软件对图像尺寸进行标定,使计算机中图像的像素所代表的尺寸与试验标尺测定的切片真实长度相等,因采集到图像为RGB模式需进行二值化处理,处理后如图4所示。
在二值化处理结束后,使用ImageJ软件进行图像的定量分析,得到切片中某一颗粒截面面积。随后按面积等效原则求出相应的等效圆直径。将切片内颗粒编号,然后进行切片内所属各颗粒的粒度判断。在任一所切截面区域,颗粒的切片数量及其最大等效圆直径与标准粒度在Z方向上的关系如表1所示。按面积等效原则求出的最大等效圆直径应该接近标准粒度,当切片数相同时按最大等效直径确定标准粒度。通过某一颗粒所占切片数及最大等效直径确定颗粒粒度范围,并给出其所在区间的粒度初值。对于只占一个切面的颗粒或较小空白处,可按10 mm颗粒给定初值。

图2 堆积体等效图Fig.2 Plane equivalent image ofaccumulation body

图3 切片原始图Fig.3 Original slice image

图4 切片二值化图Fig.4 Slice binarization image

表1 颗粒的切片数量及其最大等效圆直径与标准粒度的关系Table 1 Relationship between the slice number and maximum equivalent diameter of particles and the normal diameter

图5 切片质心图Fig.5 Slice centroid image

图6 颗粒切片中的几何关系Fig.6 Geometric relationship of particle slices
在按上述方法处理之后,一些颗粒会出现过接触或悬浮状,需要对模型内颗粒进行接触化后处理。采用基于离散单元法(Discrete Element Method,DEM)开发的离散元软件EDEM支持的颗粒工厂编译方式,将模型内置到颗粒工厂中以EDEM依赖的颗粒接触理论重构堆积体。
试验共制作了10组熟料堆积体,每个固化熟料获得6~8个有代表性的切片,共获得65张有效图片,共统计到1 363个数据点。
3 预测模型建立
熟料堆积过程与神经网络中的时间序列问题较为符合,按这类问题的模式建立熟料堆积预测模型。堆积体一般由各个颗粒在一段时间内逐渐聚合而成,在颗粒堆积完成后,每一颗粒的终态都对应堆积过程中某个时间点,各个颗粒在时间上表现出明显的先后顺序,集合中颗粒Z坐标的逐渐增加就是一个有力支撑。因此可按照神经网络中的时间序列模式解决熟料堆积问题。为了获得足够长的序列,按照组别在Z方向上随机排列,组内顺序不变原则组合数据集。构建完成后颗粒集合体的输入向量是时间的函数,堆积体的半径与坐标数据如图7所示。

图7 堆积体的半径与坐标数据Fig.7 Radius and coordinate data of the accumulation body
按以上分析,可选择非线性自回归(Nonlinear Autoregressive with Exogenous Input,NARX)神经网络来构建预测模型。将颗粒的粒度值作为输入,质心三维坐标作为输出,颗粒质心三维坐标的下一个值可由颗粒坐标的先前值和粒度的先前值回归得到。将采集到的数据进行分割,然后利用贝叶斯正则化方法训练网络,以均方差为性能指标,训练完成后使用自相关函数和互相关函数进行验证。
3.1 网络结构
数据集收集完成后需进行归一化处理,网络结构选定后其中的输入和输出需要定义。
nm=2(n-nmin)/(nmax-nmin)-1
(1)
式中:nm为归一化后的输入向量;n为输入向量元素;nmin为输入向量每一维度上最小值的向量;nmax为输入向量每一维度上最大值的向量。首先将数据集按式(1)进行归一化。归一化后的数据通常在[-1,1]标准的范围内,便于网络的训练,归一化后的半径与坐标数据如图8所示。
NARX神经网络是一个带有外部输入的非线性自回归网络,广泛用于预测问题和动态建模[12]。选择其作为堆积体建模的网络结构。NARX网络结构如图9所示。
NARX模型的定义方程如下:
y(t)=f(y(t-1),y(t-2),…,y(t-ny),u(t-1),u(t-2),…,u(t-nu))
(2)
式中:y为因变量输入信号;t为时间;u为自变量输入信号;ny为跟因变量y相关的自然数;nu为跟自变量u相关的自然数。公式(2)可以这样理解,t时刻的输入信号与t-1到t-n时刻的自变量和因变量有关。
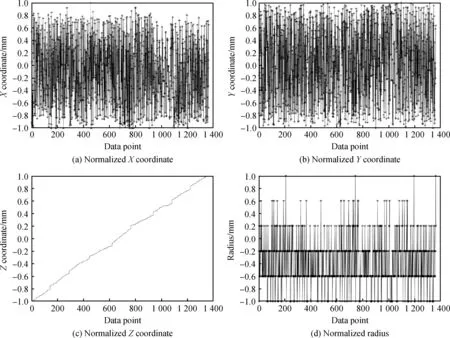
图8 归一化后的半径与坐标数据Fig.8 Normalized radius and coordinate data
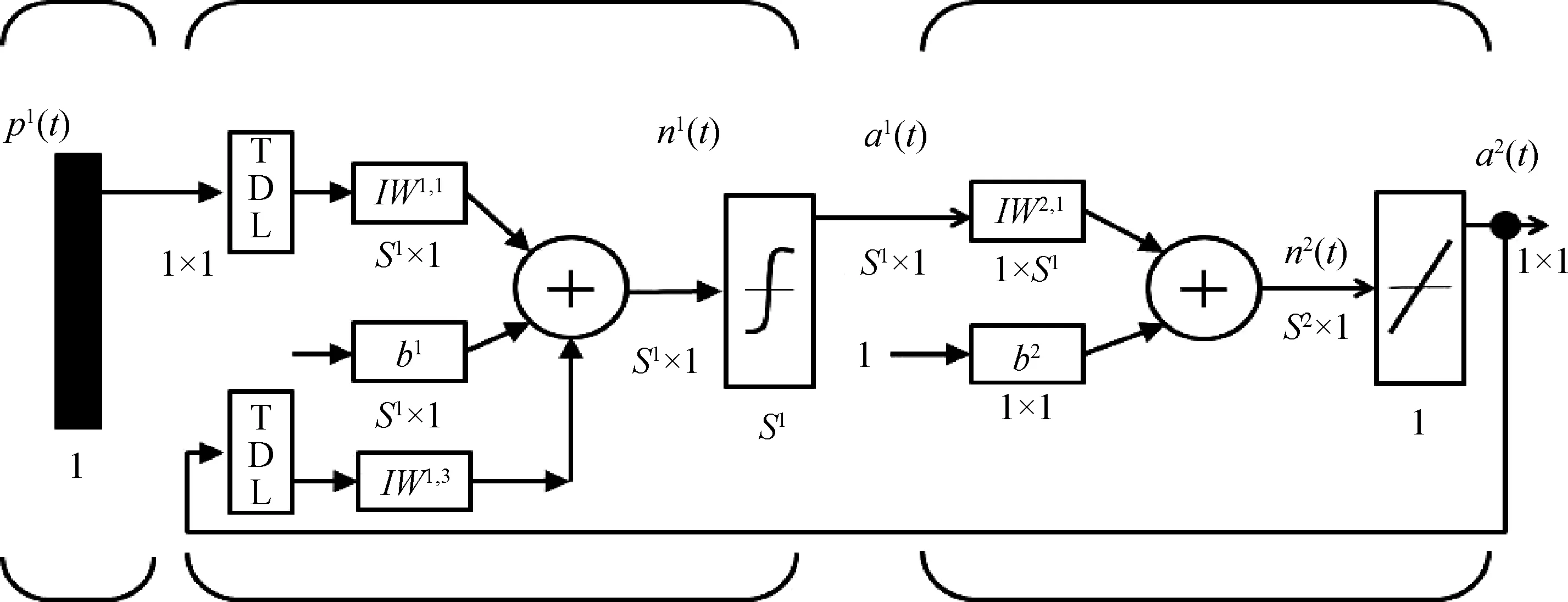
图9 NARX网络结构Fig.9 NARX network structure
网络训练时将颗粒半径R作为输入,将颗粒的质心三维坐标q作为输出。构造一个元胞数组p作为输入值,该元胞数组包含先前的输入和输出元素。任一颗粒的当前质心三维坐标既受其粒度值又受相接触颗粒的粒度值和质心三维坐标影响,在网络中表现为抽头延长线(Tapped Delay Line,TDL)[13]的长度,最终抽头延长线的长度需要根据训练效果而确定。使用串并联结构配置网络。
输入值p:
(3)
目标为下一个输出值t:
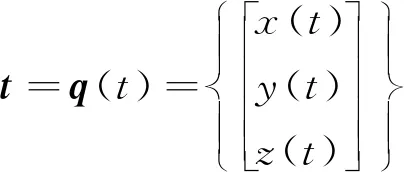
(4)
3.2 网络训练
训练时采用贝叶斯正则化方法,选择均方误差(MSE)作为性能指标。
训练之前需要将数据集进行分割,切片试验中共采集到1 363个有效数据,按式(5)进行数据集划分[14],其中ropt为最优划分率,m为网络结构参数[15],即网络结构中权值和偏置值的总和。因为训练时使用了贝叶斯正则化训练算法,所以不需要单独划分验证集,由于将熟料堆积问题处理为时间序列问题,选择最后连续的集合作为测试集。使用Widrow/Nguyen方法初始化权值[16]。

图10 均方误差随迭代次数的关系Fig.10 Relationship between mean square error and iteration number
使用贝叶斯正则化训练方法,该方法包含贝叶斯分析和正则化法两个概念,Mackay[17]对其进行过细致的研究,并提出了描述性改进。贝叶斯分析最早由Bayes提出[18],广泛应用于统计学,正则化法常用于提升网络的泛化能力。贝叶斯正则化方法在训练时会自动选择正则化参数[19],并将神经网络置于贝叶斯统计框架中。正确的正则化参数可使网络具备良好的泛化能力,正则化概念最早由Tikhonov提出[20]。另外,贝叶斯正则化方法在训练时会计算一个有效参数数量[21]。当网络结构参数总数接近有效参数数量时,说明网络规模太小,应该增大神经元数或者抽头延长线数;当网络结构参数总数远大于有效参数数量时,说明网络规模太大,可以适当减小网络规模。通过对两者进行比较可以帮助寻找到最简网络,最简网络可以避免数据过拟合并减少计算时间。
对网络进行多次训练发现性能函数MSE曲线相似,说明网络没有收敛到局部极小值。均方误差随迭代次数关系如图10所示。经验证网络中抽头延长线设为20,神经元设为10,此时网络最小,训练效果较好。这里网络中有843个结构参数,按式(5)计算,训练集取总数据的98%,测试集取2%。
(5)
3.3 网络验证
使用自相关函数和互相关函数验证网络。训练好的网络应该具备两个特性,预测误差应当在时间上不相关,预测的误差应当与输入序列不相关[22]。
自相关函数Re(τ):
(6)
式中:e(t)表示t时刻的误差;e(t+τ)表示t+τ时刻的误差;τ为时间增量;Q为总时间。
定义Re(τ)的置信区间:
(7)
网络在标准化后训练的预测误差的自相关函数如图11所示,虚线为置信区间范围。从图中可以看出自相关函数在0时是一个脉冲,其他情况下,函数值为0,所以预测误差在时间上不相关。
互相关函数Rre(τ):
(8)
式中:r(t)表示t时刻的输入;e(t+τ)表示t+τ时刻的误差;τ为时间增量;Q为总时间。
定义Rre(τ)的置信区间:
(9)
式中:Rr(0)表示输入r(t)的自相关函数。
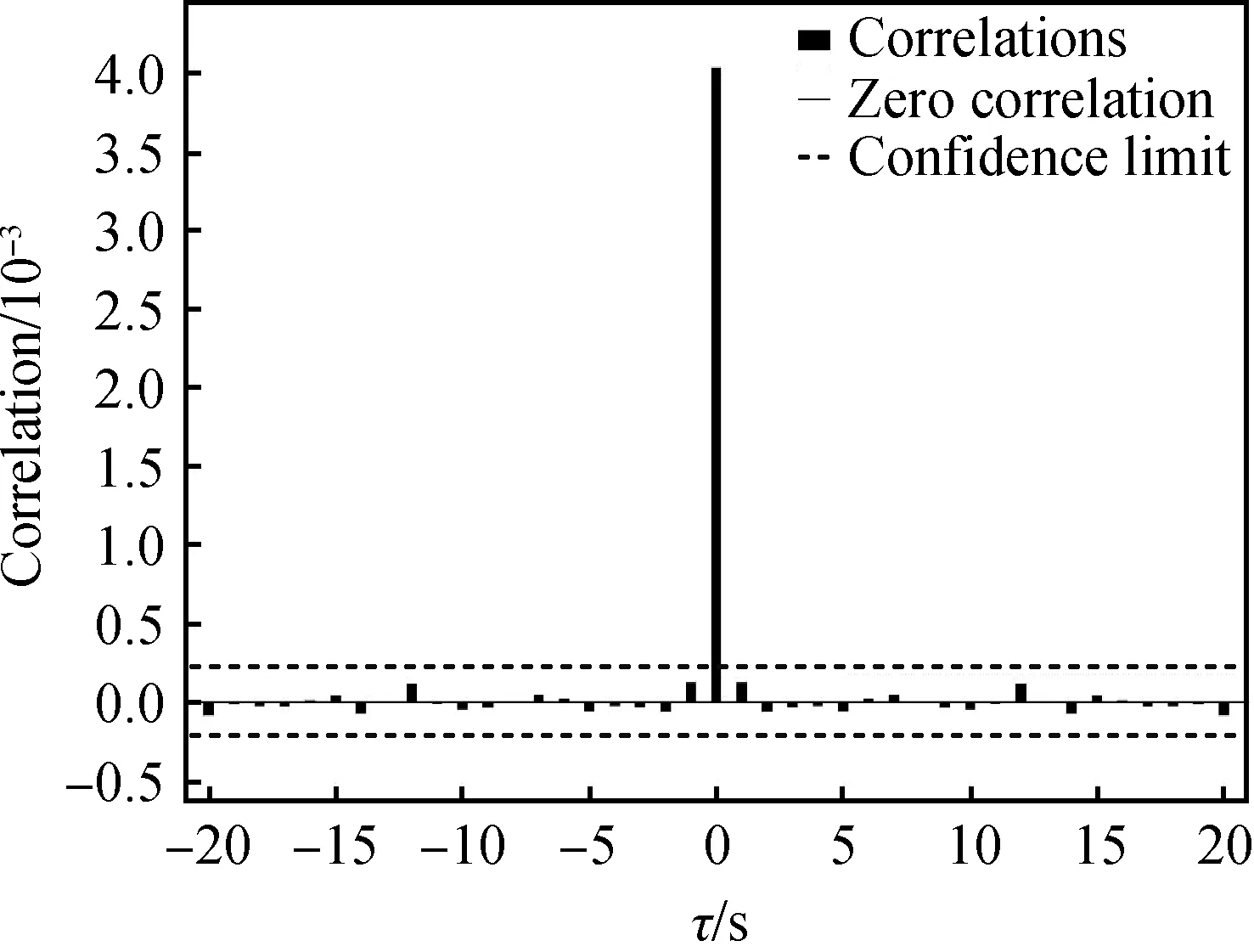
图11 自相关误差函数图Fig.11 Autocorrelation error function diagram
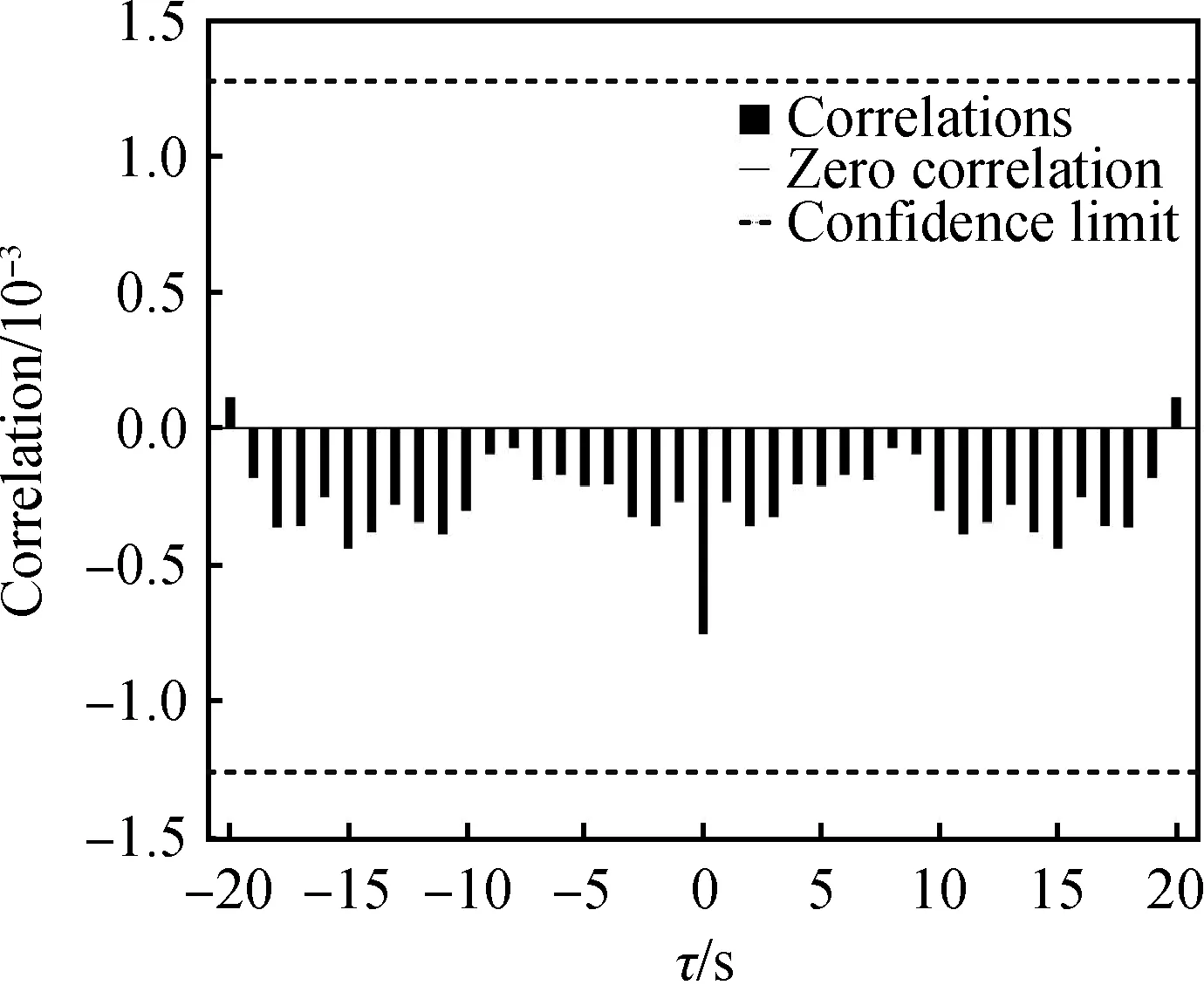
图12 互相关误差函数图Fig.12 Cross correlation error function diagram
网络在标准化后训练的预测误差的互相关函数如图12所示,虚线为置信区间范围。从图中可以看出互相关函数在置信区间内,所以预测误差与输入序列不相关。
通过以上分析表明已经建立完成一个精确的预测模型。最终预测模型的误差如图13所示。
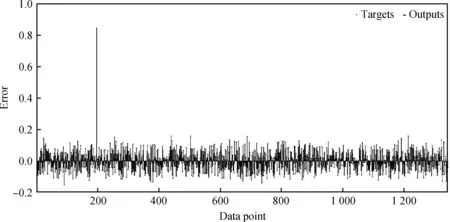
图13 预测误差Fig.13 Predictive error
从图13可以看出归一化后的训练集和测试集误差接近,说明网络没有进行外推,总体误差较小,在-0.2~0.2之间,说明网络能力足够。网络模型在一定程度上可以满足堆积体建模的要求。
4 结 论
(1)水泥熟料堆积体的模型比较复杂,神经网络功能强大且善于解决工业问题。熟料堆积过程与神经网络中的时间序列问题类似,按照时间序列模式处理熟料堆积过程。选择NARX网络结构,构建一个包含输入和输出元素的元胞数组,使用贝叶斯正则化方法训练网络,以均方误差作为性能指标。
(2)训练神经网络时需要先获取原始数据。为了获取熟料堆积体的结构信息,以工业生产的水泥熟料为材料进行了堆积试验,并制作了一系列熟料切片,通过对切片图像进行处理和统计获得了堆积体中颗粒集合的粒度和质心三维坐标。
(3)对训练后的神经网络进行验证分析,预测误差的自相关函数和互相关函数都位于置信区间内,说明误差与误差,误差与输入之间没有相关性,模型可以正确运行。归一化后预测模型的总误差在-0.2~0.2之间,网络模型在一定程度上可以满足堆积体建模的要求。

