遵循学生认知 让“深度学习”真实发生
——以“分数的基本性质”教学为例
浙江省东阳市六石中心小学 韦雅玲
有关教育家认为:深度学习是在理解学习的基础上,学习者能够批判性地学习新的思想和事实,并将它们融入原有的认知结构中,能够在众多思想间进行联系,并能够将已有的知识迁移到新的情境中,做出决策和解决问题的学习。强调深度学习要重在学生的理解、反思、建构以及迁移运用和问题解决。通过组织有效的教学活动,让学生把相同数学结构的问题统整起来,实现学生对已有知识的深度整理,才能让学生进行深度的学习,让学习真实发生。本人根据亲身经历的一堂课——五年级上册《分数的基本性质》与大家交流。
一、遵循认知起点,梳理关联,让深度学习有根可寻
(一)把握教材逻辑起点
逻辑起点是指根据数学知识之间的内在关联,学生学习新知时应具备的知识、技能和方法等基础,通过追根求源找到原有经验是学生主动建构的根基。在课堂教学中,教师常常会从学生熟悉的生活情境入手,通过一定的情境激活学生的已有生活经验和知识经验,进而帮助学生积累和形成新的活动经验,已有的知识经验就是这个新知的生长点。例如“分数的基本性质”一课,是在学生学习了分数的意义、分数与除法的关系、商不变的规律等知识的基础上进行教学的,这些经验就是学生学习分数基本性质的逻辑起点。
(二)基于前测分析学生的现实起点
学生已有的经验是学生数学学习的现实起点。新知的教学需要关注学生已有的认知起点,去进行有效的改造、唤醒与激发。为了更好地把握学生现实的知识起点,要在课前组织学生完成一份前测练习。
【教学片段1】
出示前测中收集到的正方形、线段图或数轴、文字表述等方法。
方法一:画图

方法二:画图
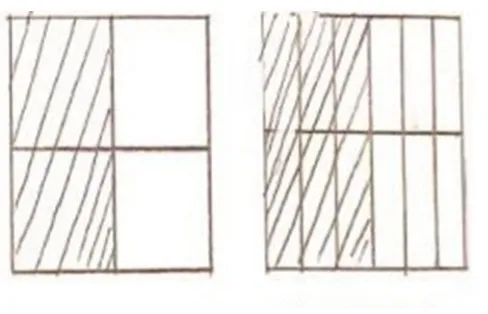
方法三:文字

方法四: 文字

方法五:分数与除法的关系
方法六:商不变的规律

教师:这些方法之间有什么相同的地方?有什么不同的地方?(结合学生汇报,适时点拨)
数学知识的逻辑起点和学生认知的心理起点是学生深度学习得以展开的先决条件。基于以上两个维度的分析,有利于学生在原生态的问题背景中展现真实的思维,让学生的数学思考看得见,抓得着,让学生的学习效果达到最大化,让学生的深度学习像呼吸一样自然,实现经验与数学知识的无缝对接,保证学生的认知朝着正确的方向生长。
二、遵循认知结构,迁移经验,让深度学习有枝可攀
结构主义教育家奥苏贝尔在有意义言语学习理论的基础上提出了认知结构迁移理论,其目的是塑造学生良好的知识结构体系。深度学习恰恰要求的便是让学生不仅要理解知识的本质,更要形成知识的结构体系。
【教学片段2】
教师:看到分数的基本性质,你想到了什么?
学生:商不变的规律。教师:是的,分数与除法,无论形式上,还是意义上,都是相通的。讲到这,老师不禁想到了小数的性质。我们以0.7为例,这是小数的性质,这是分数的基本性质,你能用分数的基本性质去解释小数的性质吗?学生:0.7就是7/10,0.70就是70%,0.700就是700%。教师:对啊,你看得真仔细。
小结:小数的末尾添一个0,就相当于分数的分子和分母乘10,小数的末尾添两个0,就相当于分数的分子和分母乘100。“商不变的规律”和“分数的基本性质”进行了类比,又用“分数的基本性质”理解“小数的性质”,尽管它们叙述的形式不一样,但本质是相同的。
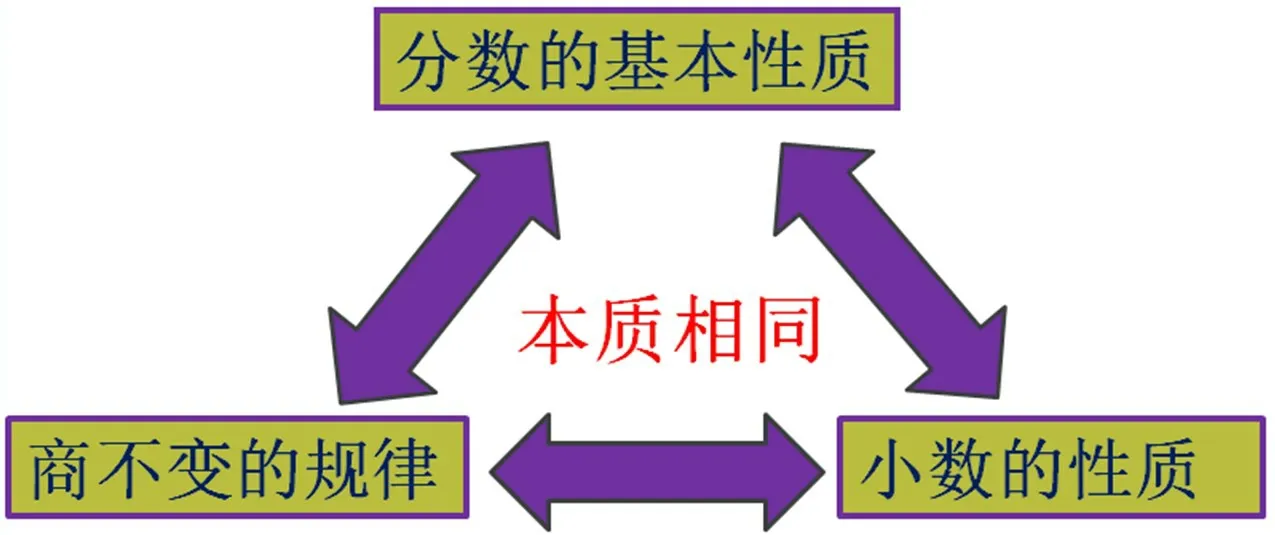
解决问题的方法是多样的,沟通这些方法之间的联系,帮学生理清各种知识之间的共同点,从而获得多种解决问题的方法。在探究过程中,教师着力帮助学生把积累的经验迁移到新的问题情境中,再融合各种方法,构建新的认知结构。这个过程是无痕的,看似轻松简单的对话,实则暗藏了经验间的无形碰撞,学生顺着交流的升华,让深度学习更加枝繁叶茂。
三、关注认知延伸,活用模型,让深度学习有果可获
数学家波利亚曾经主张,与其做大量的难题,不如把一道题的各个侧面研究理解透彻,让每一位学生主动参与去寻找答案,展示不同的思维层次,形成高阶思维。教学中制造认知冲突或合适的问题情境引导学生自主探究,获得对数学知识新的认识和理解。构建有序思维,活用模型,解决挑战性问题,这也是深度学习的特质。
总之,小学数学的深度学习,不是提升学生的学习难度,而是遵循学生认知起点,完善认知结构,重构知识网络,发展高阶思维,感悟数学思想,提升数学素养。引领学生深度参与、深度体验、深度发展,才能让学生真正在数学学习中乐此不疲,让深度学习真正发生。

