富水电地区电网低频振荡风险抑制策略
贺忠尉,向 勇,李大虎,袁志军,黄文涛,何 俊
(1 国网湖北省电力有限公司恩施供电公司,湖北 恩施 445000;2 湖北工业大学电气与电子工程学院,湖北 武汉 430068;3 国家电网湖北省电力有限公司,湖北 武汉 430077,湖北 武汉 430068)
随着我国区域电网供电规模不断扩大,多种形式能源并入到电网导致当前电网特性变得复杂。由于多种能源并网以及网架结构的改变使得电力系统开始呈现出不同程度的阻尼不足现象,导致了低频振荡现象的产生[1]。目前国内外的研究人员对低频振荡展开了一些研究[2],从机理分析的角度提出了各种低频振荡抑制手段,根据低频振荡发生的原因提出了各种理论和方法,当前分析方法中最为常见的方法包括两种[3-5],分别是小干扰分析以及信号分析法。结合当前振荡的情况并且结合发电机监测数据来确定振荡源是当前主要研究方法[6-7]。
对于富水电地区,小水电群点多面广、网架薄弱,存在地区之间弱互联导致的弱阻尼振荡模式[8],且小电网或以水电为主的电网调速器稳定问题突出,调速器的参数与系统稳定性关系尤为密切[9]。现有研究针对弱(负)阻尼低频振荡模式,可以通过增强系统阻尼加以抑制,如加强电网结构、采用直流输电技术、输电线路采用串联补偿电容、加装静止无功补偿器(static var compensator SVC)、附加电力系统稳定器(power system stabilizer, PSS)等[10]。但由于富水电地区本身存在的特性,低频振荡问题更为复杂,使得采用PSS装置时,参数整定的因素多变,不利于PSS参数选取,且PSS参数的适用性低。目前,富水电地区低频振荡风险影响因素及PSS参数优化相关的研究较少。
而恩施电网水电、风电等新能源电源众多,机组参数对恩施电网低频振荡特性密切相关。为构建川渝电网与西藏电网的联网,从而实现西南电网同步运行[11],国家电网公司于2019年上半年完成了渝鄂背靠背直流工程的投运,该工程中的施州换流站位于恩施境内,恩施电网属于富含小水电机组的电网,这种交直流耦合的富含大量小水电机组的电网存在着低频振荡风险,本文以恩施电网为案例展开仿真分析研究,并采用粒子群算法来进行优化,求出最佳发电机组参数,提升富水地区电网系统阻尼水平,降低电网发生低频振荡的风险。
1 富水电地区电网低频振荡影响机理
1.1 富水电地区网源结构影响
富水电地区以水电机组参与发电为主,常规火力发电占比较小,在研究富水电地区电网的低频振荡问题和电力系统稳定器的应用时,仍然以单机无穷大系统(图1)为例,研究系统的阻尼水平。

图 1 单机无穷大系统示意图
单机无穷大系统的控制系统采用图2所示的菲利普-海富隆模型[12-13]进行简化描述,本文通过附加原动机调速环节,进一步区别分析水电机组,火电机组参与下的富水电地区阻尼特性,系统阻尼水平由阻尼转矩系数KD表征。
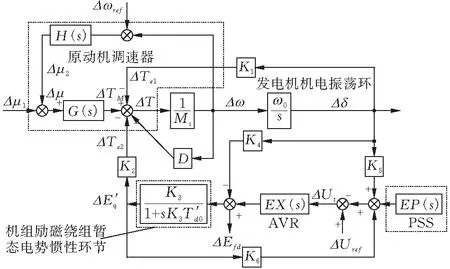
图 2 附加调速器的单机无穷大系统菲利普-海富隆模型
根据图2所示的单机无穷大系统菲利普-海富隆控制数学模型,发电机输出转矩
ΔT=ΔTM-(ΔTe1+ΔTe2)=
在无PSS情况下发电机励磁系统的电磁转矩
采用阻尼转矩法,取低频振荡频率ωd,令s=jωd,得:
KS=-K2K5KEXcosφEX
(1)
KEX和φEX为励磁控制系统的参数及系数K3、K6的函数;同步转矩系数KS,阻尼力矩系数KD既是励磁控制系数的函数又是同步电机运行工况(K2、K5、K6)的函数。
原动机调速系统传递函数有:
ΔTm=G(s)·Δμ
ΔPm=ΔTm·ω
(2)
Δμ为开度增量,在同步转速下,取ω=1,则发电机输入机械功率ΔPm=ΔTm,输出功率ΔP=ΔT。
1.1.1 富水电地区机组功率调节特性发电机组的功率调节特性通过发电机功角δ0影响系统阻尼水平,其功率调节则通过原动机调节机构控制。
1)水电机组的功率调节是根据水轮机通过改变导水机构开度μ来控制流量大小,从而改变输出机械转矩,进而控制发电机的输出功率。由于水锤效应影响,水轮机机械转矩大小随水轮机阀门的变化存在一定的时滞。考虑水锤效应,典型的水轮机功率调节传递函数为:
G(s)=(1-stw)/(1+0.5tw)
(3)
式中:tw为水锤时间常数,一般为0.5~5.0 s。
2)火电机组的功率调节是通过汽阀开度来调节进汽量,进而改变输出转矩。受汽容效应影响,汽轮机转矩变化将滞后于汽阀开度变化,典型的无再热型汽轮机功率调节传递函数为:
G(s)=1/(1+stt)
(4)
式中:tt为汽容时间常数,一般取0.1~0.3 s。
将式(3),式(4)分别代入式(2)可知,水轮机功率调节属于非最小相位环节,输出量比输入量存在较大的相位滞后,使得整个调速系统存在低频振荡的风险;而汽轮机功率调节属于最小相位环节,输出量比输入量也有一定的相位滞后,但滞后量比水轮机的要小。
由图1所示的单机无穷大系统为基础进行仿真分析,通过改变调速器的频率给定来研究水电机组和火电机组调速系统的功率调节特性。测试机组发电功率为800 MW,功率全部被无穷大母线吸收。调速器的频率选定为上阶跃特性,仿真时间t<2 s时,频率f=50 Hz;仿真时间t≥2 s时,频率f=50.2 Hz;式(4)、式(3)取极限状态,tt分别取0.1 s,0.3 s;tw分别取0.5 s,5 s。水电机组与火电机组的机械功率变化曲线如图3所示。
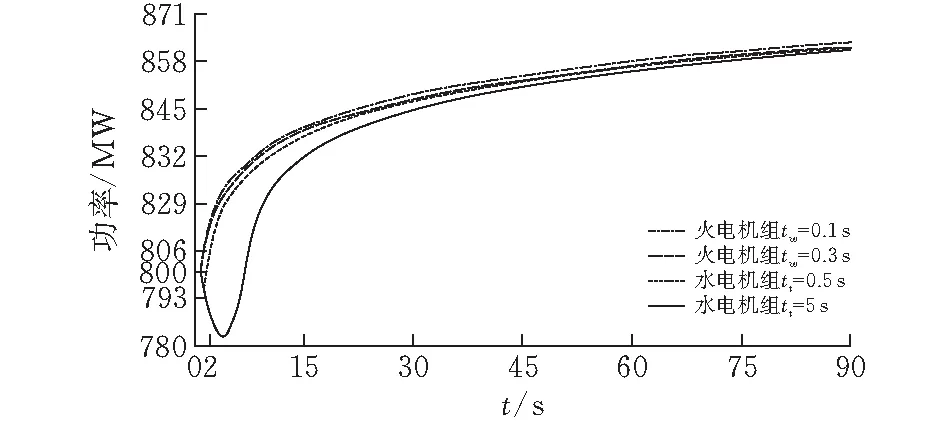
图 3 水电机组与火电机组功率调节特性对比曲线
从图3可以看出,水电机组的机械功率调节滞后于频率变化,且在初始阶段存在功率反调现象,并且随tw增大,机械功率反调强度和持续时间加剧;火电机组的机械功率调节虽然也存在滞后现象,但不存在功率反调现象,随着tt增大,火电机组的机械功率调节的滞后特性加剧。
机械功率调节导致的不平衡功率加大,电网将存在频率振荡风险。但在实际电网中,不同火电机组间由于tt相近,功率调节特性总体相差不大,阻尼仍呈正阻尼,而水电机组tw相差较大,功率调节特性存在较大差异,将呈现负阻尼现象,在富水电地区这种现象更为显著。
1.1.2 富水电地区联络线阻抗特性根据图1所示的单机无穷大系统,由其等值电路[14-15],可知图2的控制数学模型中传递函数:
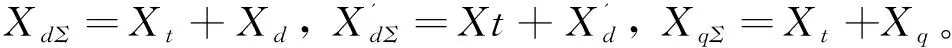
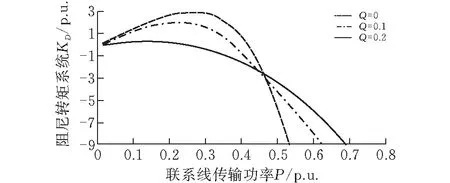
由式(1)可知,阻尼力矩系数KD主要通过对模型系数K2,K5的影响表现出来,富水电地区水电厂通常远离负荷区,长距离输电,具有联络线电抗Xt大的特点。不同发电机电抗XG下,阻尼转矩系数随联络线长度变化的关系如图4所示,因此,长链条、弱互联电力系统的低频振荡问题通常更为严重。
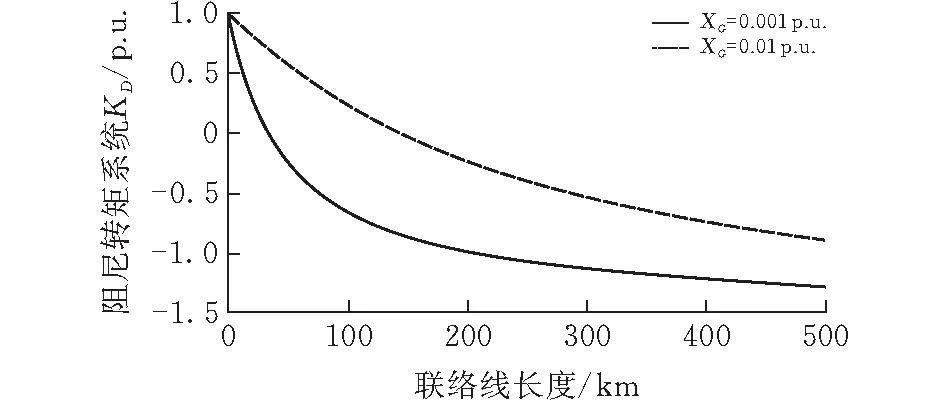
图 4 阻尼转矩系数与联络线长度关系
1.2 运行(开机)方式的影响
从上文分析已知阻尼力矩系数KD主要取决于K2,K5,由式(7)可知K2为正数,K5的数值除了与线路电抗Xt相关外,还与发电机功角δ0有关,即联络线功率传输相关。图5为富水电地区接入的三机链式系统对冲运行方式,由于对冲方式下联络线潮流最重,故系统动态稳定水平最低[16]。
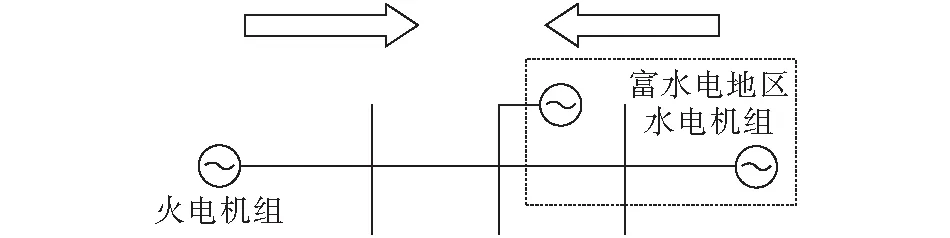
图 5 三机链式系统对冲运行方式示意图
对于富水电地区,通常水电占比70%以上,本文通过参与系数K水,K火对水电机组与火电机组的参与水平进行表征,采用线性加权表示系统阻尼水平,即:
KD=K水KD水+K火KD火,K水+K火=1
(5)
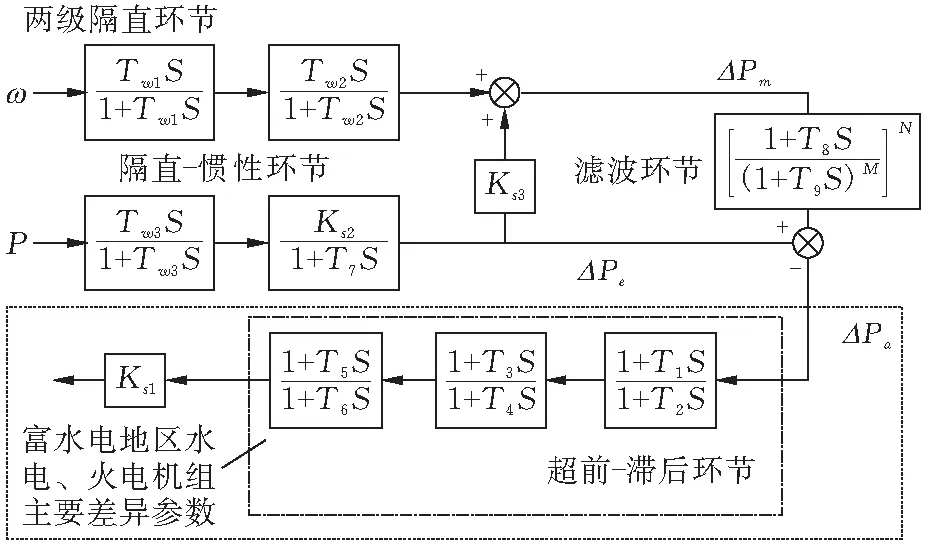
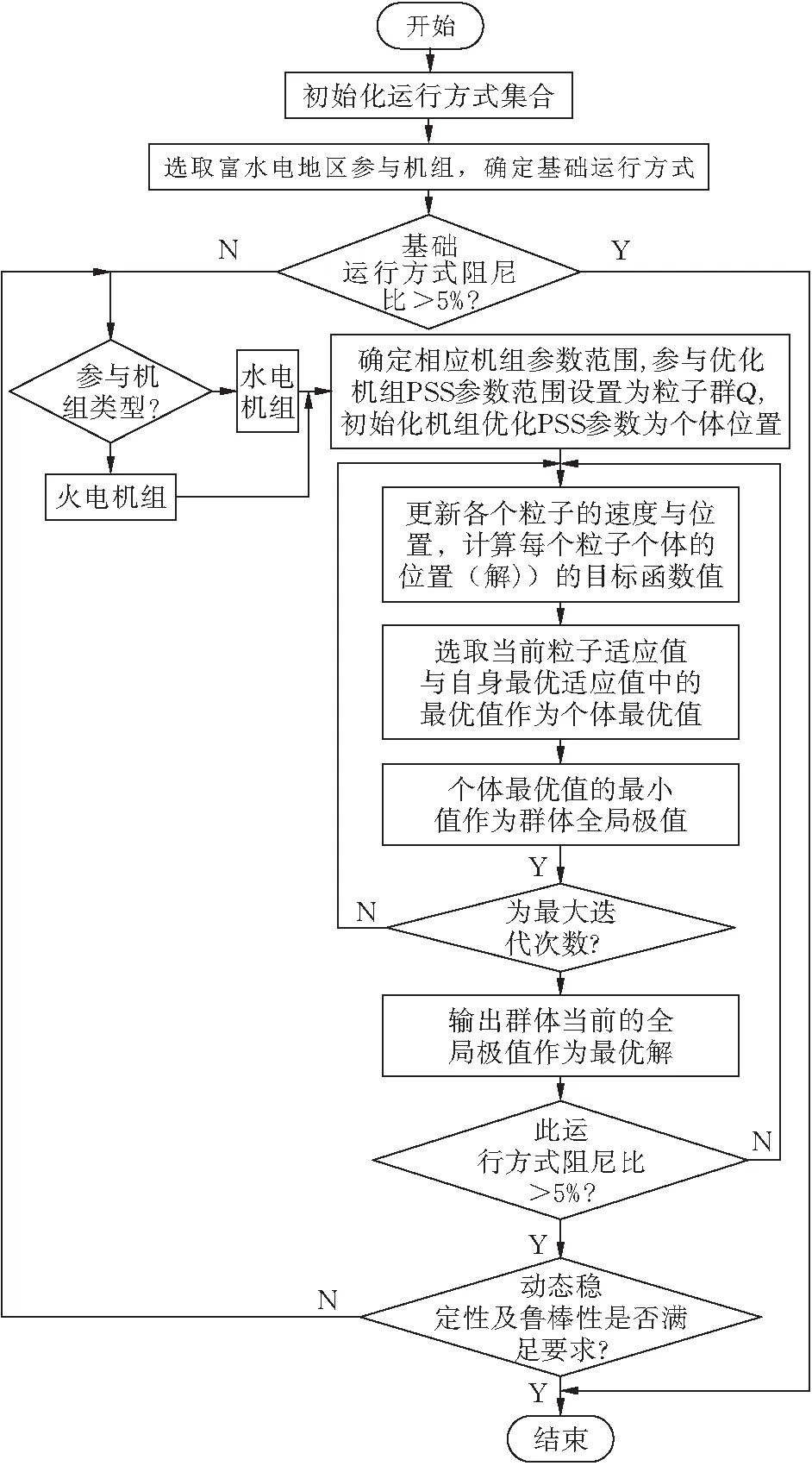
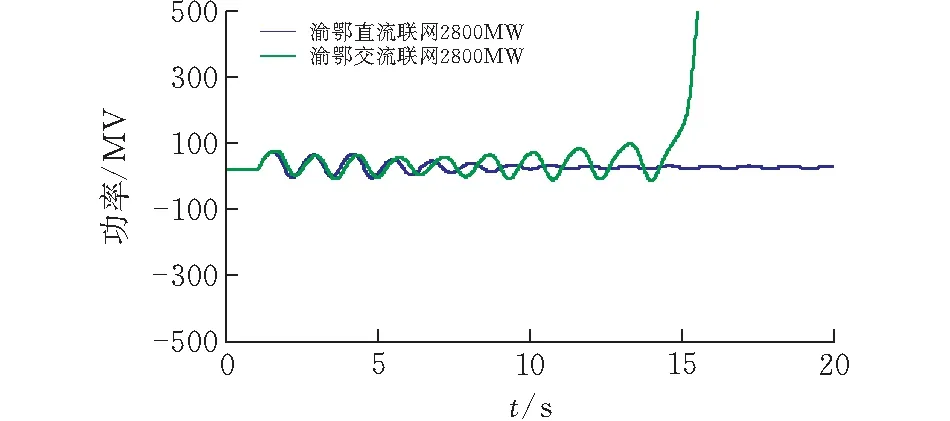
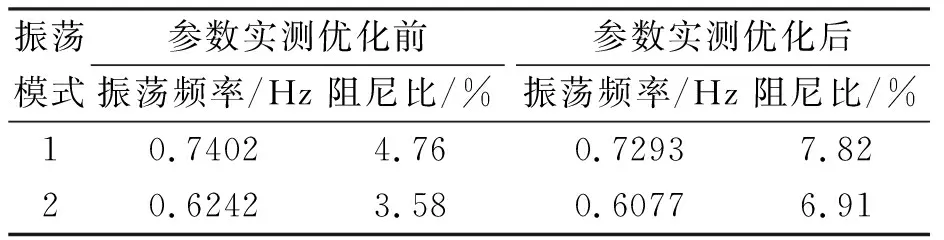
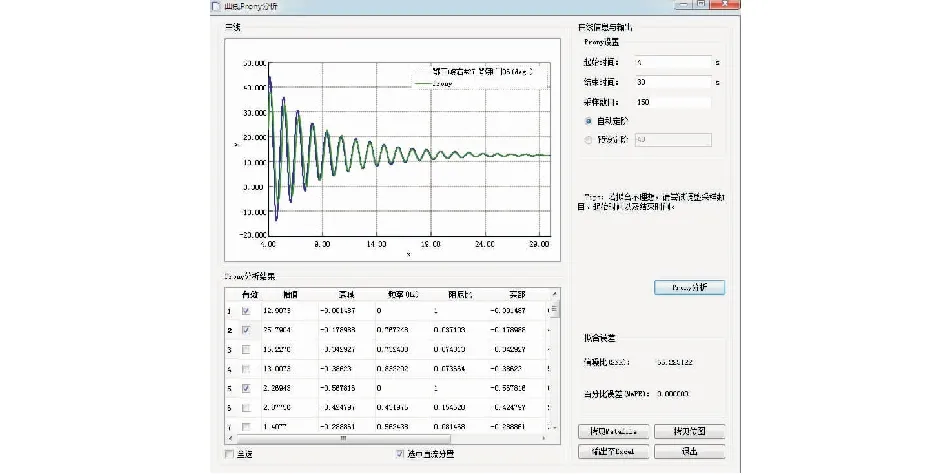
式中:富水电地区,水电占比70%以上,参与系数K水常取0.7以上,K火常取0.3以下,由上文分析的发电机机组功率调节特性可知,通常KD水 图 6 阻尼转矩系数与联络线功率关系示意图 富水电地区电力系统运行(开机)方式决定联络线输送功率: 1)在用电低谷时,离负荷中心较近的火电厂减少开机,功率由远方的水电机组送出,这时联络线功率增大,阻尼减弱。 2)丰水方式下,水电机组大量运行,富水电地区电力大量向主网输送,易造成潮流分布不均,联络线功率增大,阻尼减弱。 上述分析可知,富水电地区,高占比的水电机组是导致低频振荡的主要原因。电力系统稳定装置(PSS)是抑制低频振荡的有效手段之一,采取对发电机组的励磁系统配置电力系统稳定装置(PSS),尤适用于单机(或单个电厂),对电网之间的局部低频振荡效果最佳,且具有技术成熟和配置简单经济的特点。 电力系统稳定器(PSS)基本原理就是利用软件或硬件对附加控制信号ΔP、Δω等进行处理,使得输入信号产生一个相位移φPSS,以此达到增加系统稳定性的目的[14]。本文PSS采用加速功率型PSS2A,具体模型及相关参数如图7所示。 图 7 PSS模型及相关参数 ω为发电机轴的旋转角速度;P为发电机的有功功率;高频输入为机械功率;TW1、TW2、TW3为隔直时间常数;KS1为PSS增益系数;KS2、KS3分别为功率增益系数和功率及转速转换系数;T1~T6为超前-滞后时间常数;T7为惯性时间常数;T8、T9为高阶滤波器的时间常数;M、N为高阶滤波器的阶数。 由图7所示PSS参数模型,一般情况下,针对某一发电机其隔直、信号滤波、惯性补偿及滤波等信号处理环节的时间常数固定不变,富水电地区机组PSS主要通过调节增益系数KP以及超前-滞后环节的时间常数T1~T6来抑制电力系统的低频振荡现象。因此,富水电地区多机组的传递函数可简化为: (6) 特别的,由上文分析,水电机组为主的富水电地区,水电机组由于存在机组的反调特性,水电机组整定参数与火电机组参数存在差异,其导致的弱阻尼特性更强,需要相位补偿,大多针对超前时间常数优化,主要体现在超前时间常数T1,i、T3,i、T5,i上。应采取差异化参数优化。 式(6)中:针对富水电地区,参与机组类型不同,取i为水电、火电发电机组标识;Ri为PSS输入信号,如图7所示,选取为电磁功率偏差ΔP与转速偏差Δω叠加后的加速功率ΔPa;Ui为PSS输出信号;Ai(s)为信号处理环节的集合。 在对发电机PSS参数进行优化的过程中,需要遵守两个原则,首先第一个原则就是优化选择合适的相位补偿角φPSS,使得φEX+φPSS=-π/2,通过优化选择合适的Ai(s)参数来确保发电机PSS单元的阻尼分量足够大,来确保KD足够大;第二方面就是通过优化参数来提升相位补偿增益,达到较好的PSS阻尼效果。相位补偿可根据PMU装置及阻尼转矩分析计算得到,但整定参数还需进一步优化,以适应富水电地区。上文分析可知富水电地区存在高占比的水电机组,导致因弱阻尼产生的低频振荡。其振荡机理复杂,因素繁多,导致水电,火电机组PSS参数整定优化不易,为此提出基于粒子群的PSS参数优化方法。 2.2.1 基于粒子群的PSS参数优化粒子群算法是Kennedy于1965年提出的一种智能化算法,该算法能够通过建模目标函数并进行优化求解,粒子群算法能够建立目标函数,并且通过控制粒子的飞行方向来确定目标函数[17]。 假设在一个M维的目标搜索空间里,一个粒子群包含m个粒子,其中第i个粒子位置可由M维向量表示为vi=(vi1,vi2,…,viM),飞行速度表示为vi=(vi1,vi2,…,viM)。粒子群中,粒子在解空间中的个体最佳位置为gi=(gi1,gi2,…,giM);所有粒子所经历的全局最佳位置为gi=(gi1,gi2,…,giM)。在第n次迭代中,粒子i根据下式更新速度和位置。 vin=w·vin-1+c1·Rand·[pin-1-xin-1]+ (7) xin=xin-1+vin-1 (8) 式中:w为惯性因子;Rand为[0,1]范围内的随机数;c1和c2为加速因子;n为迭代次数;粒子数i=1,2,…,m。 1)PSS优化的目标函数和约束条件 多机组常规PSS参数优化以系统阻尼比为优化目标,富水电地区系统以高占比水电机组为主要特征。根据本文推导的式(1),以及定义的式(5),引入富水电地区参与机组比例,定义i运行方式下富水电地区主导低频振荡阻尼比 式中:ξ水i,j为i运行方式的主导振荡模式下,第j台水电机组的阻尼比;ξ火i,k为相应的第k台火电机组的阻尼比;K水i、K火i为i运行方式下参与主导振荡模式中的水电机组、火电机组占比;D、H分别为水电、火电参与主导低频振荡机组台数。 多运行方式下,PSS参数优化后的系统阻尼比应综合满足系统动态稳定性与鲁棒性[18]。当主导振荡模式阻尼比为0.015时,可视为系统临界动态稳定状态,按照电力系统稳定要求,系统主导振荡模式阻尼比应大于0.05。本文取动态稳定性指标Z,鲁棒性指标L,来指导富水电地区水电机组高占比下的PSS参数优化方向,并通过线性加权定义PSS优化目标f,引入式(12),综合考虑PSS与励磁系统的性能。 f=ω1Z+ω2L (9) (10) (11) 根据Pontryagin提出的极小值原理[12],可将PSS参数优化问题转化为求解如下带有约束的优化问题: (12) 式中:M为富水电地区参与优化机组的总台数,其中水电机组D台,火电机组H台;Kp,i为第i台参与优化机组的PSS增益;T1,i、T3,i、T5,i为超前-滞后环节中第i台机组的待优化时间常数。 由于火电机组与水电机组的差异,其参数的寻优范围有一定差异,并影响算法寻优范围。火电机组Kp火的典型取值范围是[0.1,100],T1火的典型取值范围是[0.01,1.0],T3火的典型取值范围是[0.01,1.0],T5火的典型取值范围是[0.01,1.0];水电机组Kp水的典型取值范围是[0.1,500],T1水的典型取值范围是[0.01,1.0],T3水的典型取值范围是[0.01,1.0],T5水的典型取值范围是[0.01,2.0]。 2)参与PSS优化机组的筛选 富水电地区参与机组PSS参数优化筛选,需要对该运行方式下主导低频振荡的发电机组进行参与主导模式分析,取出低频振荡影响较大的机组进行PSS参数优化。常规方式仅选取参与因子Pk,i=φk,i×ψi,k,表示模式i中第k个状态变量的相对参与程度,并未表现富水电地区弱阻尼转矩导致的低频振荡特性。本文通过动态响应因子ηDR,综合参与因子P与富水电地区阻尼转矩参数KD,惯性时间常数TJ,既反映参与度,又反映富水电地区低频振荡幅值的衰减。 式中:ηDR水(l,j)、ηDR火(l,k)为富水电地区l低频振荡模式下第j台水电、第k台火电机组的动态响应因子;P水(l,j)、P火(l,k)分别为该台水电、火电机组的参与因子。 动态响应因子越小,机组对该振荡模式的振荡衰减越快。本文拟选取动态因子前60%的机组进行PSS参数优化,即满足: 3)富水电地区基于PSO的PSS参数优化设计 按照电力系统稳定要求,为使系统具有较好的动态特性,系统阻尼比应大于5%,(此处系统阻尼比即为主导振荡模式阻尼比)。假设富水电地区需进行PSS参数优化的机组共M台,其中水电机组D台,火电机组H台,以式(12)作为系统的优化目标函数,每台机组优化参数为Kp,T1,T3,T5,则粒子群空间纬度为4,个体位置xi=(Kp,i,T1,i,T3,i,T5,i),流程及具体操作步骤见图8。 图 8 基于PSO算法的PSS参数优化流程 A)确定需进行PSS参数优化的运行方式集合,并进行初始化。 B)确定基础运行方式、主导振荡模式以及参与机组,对各方式进行小干扰分析,若基础方式阻尼比大于5%,结束优化过程;否则,进入下一步。 C)判断参与优化机组类型,火电机组还是水电机组。 D)根据初始粒子群的优化位置和优化速度,对每个粒子的初始值进行选择,并且通过合理布局来优化选择全局的极值,对目标函数进行优化选择得到结果。 E)判断迭代计算是否达到迭代次数上限,若是,则将当前的全局极值作为最优解;否则,继续进行迭代计算。 F)迭代结束后,判断本方式阻尼比是否满足条件,若是,进入下一步;否则,按式(7)和式(8)更新粒子的速度与位置,并返回步骤(3)。 G)将最优解代入所有运行方式,判断是否均满足动态稳定性及鲁棒性要求,若是,则PSS参数优化结束,否则返回步骤(2),重新选取基础方式,直至所有方式满足要求。 仿真算例采用2020年发布的恩施电网数据包进行计算,仿真工具采用PSASP(电力系统综合稳定分析程序),负荷水平采用恩施电网夏季大负荷方式,采用粒子群算法对恩施地区水电机组PSS参数进行优化,其中设定粒子群规模30,加速因子c1=c2=2.0,取迭代次上限为50次。经过30次的随机优化计算,得出优化后满足电力系统稳定要求的最优值,作为优化结果。机组参数实测及优化前后恩施相关小干扰稳定模式下的频率及阻尼比如下所示: 1)发电机组PSS参数优化前 对“三峡左一、右三~三峡右二、水布、江坪河、恩施”振荡模式进行大扰动分析,XL线路N-1故障后将激发出如图9所示的负阻尼振荡模式。 图 9 交直流联网方式下XL线路N-1故障后SX2机组功角曲线 分析结果显示,在渝鄂交流联网方式下,XL线路发生N-1故障后振荡频率约为0.75 Hz,阻尼比约为3.3%;在渝鄂柔直联网方式下,XL线路发生N-1故障后振荡频率约为0.73 Hz,阻尼比约为-1.47%,故障后约14 s,SX2机组对系统失步。系统为负阻尼,稳定性差。 2)发电机组PSS参数优化后 2019年,三峡左岸、右二电厂按照计划全部完成实测改造,恩施电网小水电机组大部分完成实测建模及动态参数优化工作,动稳问题不再是制约渝鄂柔直能力及恩施水电外送的因素。机组参数实测及优化前后恩施相关小干扰稳定模式频率及阻尼比如表1所示。 表1 机组参数优化前后恩施相关小干扰稳定模式对比 由表1可见,恩施地区机组参数优化后,恩施相关振荡模式的阻尼比均有所增加,仍对XL线路N-1故障进行大干扰稳定分析,XL线路N-1故障后功角曲线及Prony分析结果见图10。 图10 XL线路N-1故障后SX2机组功角曲线Prony分析结果 图10的Prony分析结果显示,参数实测及优化后,XL线路N-1故障后振荡频率约为0.76 Hz,阻尼比约为3.7%,为强阻尼振荡模式,系统保持稳定。 富水电地区电网电源类型众多,线路距离长,阻抗大,电源分布点较为分散,电网低频振荡特性复杂,传统方法难以很好控制低频振荡风险。本文针对富水电地区电网特点进行低频振荡影响因素分析,并提出了一种基于粒子群人工智能算法的富水电地区电网PSS参数优化方法,以恩施电网为例,仿真结果验证了本文方法的有效性,可为水电丰富地区电网控制低频振荡风险提供参考。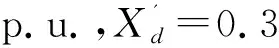
2 富水电发电机组PSS参数优化
2.1 PSS模型
2.2 富水电地区电网PSS参数优化方法
c2·Rand·[gin-1-xin-1]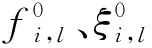
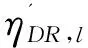
3 仿真算例
4 结论

