平面变压器电流均分的n∶1绕组布置方法

张 杰，周万东，赵小康

(1 湖北工业大学电气与电子工程学院，湖北 武汉 430068； 2 湖北中烟卷烟材料厂，湖北 武汉 430000)

磁性元件的高频损耗主要包括趋肤效应损耗和邻近效应损耗，研究趋肤效应和邻近效应产生的原因及其影响因素对控制平面变压器绕组高频损耗具有重要意义[1]。在高频工作条件下,铜箔绕组的交流阻抗、结构参数对平面变压器的损耗影响很大。针对此问题，文献[2]研究并联绕组结构的损耗特征及影响因素，提出高频工作条件下，几种低损耗平面变压器绕组的结构优化设计方案，但并没有将其进一步推广。对于PCB线圈涡流的损耗，文献[3]基于涡流场场控方程与回路电压平衡原理，建立了任意并联长形和环形PCB线圈涡流损耗解析模型。文献[4]提出一种方法来表达在高频开关电源中工作的平面变压器铜损，更精确地表达铜损特性。文献[5]研究每个绕组层内线圈电流分布对PT的漏感和交流电阻的影响，并给出基于变分法的分析推导。通过三维有限元分析模拟和物理实验，提出并验证最优电流分布。本文针对绕组损耗以及并联绕组电流均分问题，提出一种并联绕组的结构设计，以减少绕组损耗和实现并联绕组电流均分，并通过Maxwell 3D验证该结构的有效性。

1 绕组损耗

1.1 趋肤效应和邻近效应

趋肤效应产生过程如图1所示，导体电流方向与其表面涡流方向相同，与内部的涡流方向相反，这样就会导致导体表面的电流密度增大，内部的电流密度减小。一般趋肤效应用趋肤深度

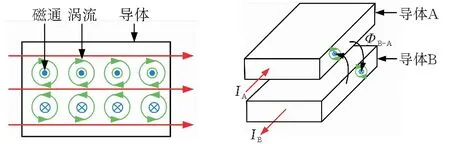
图 1 趋肤效应产生过程示意图

式中：γ为导体的电导率；μ为导体的磁导率；f为工作频率。

邻近效应的产生过程如图2所示，流过导体A、B的电流IA、IB方向相反，当电流变化时，导体A产生的突变磁通ΦA-B在导体B中产生涡流，使其下表面的电流增大，上表面的电流减小，同理，导体A中也会因为导体B产生的突变磁通ΦB-A而产生涡流，使上表面的电流增大，下表面的电流减小。

1.2 平面变压器单层绕组损耗计算

在电磁场方程中，有如下关系：

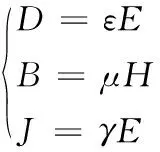
(1)

式中，H为磁场强度，J为电流密度，D为电通量密度，E为电场强度，B为磁感应强度，ε为电介质的介电常数，μ为导体的磁导率，γ为导体的电导率。将方程组(1)代入安培环路定律的微分方程，两边取旋度，根据矢量恒等式得

设场量波形为K=Kmcos (ωt+θ)，其中Km为幅值，θ为相角，有∂B/∂t=jωB，可得：

2B=jωμ(γ+jωε)B

(2)

平面变压器的绕组一般为铜箔绕组，则γ=5.8×107(S/m)，μ=4π×10-7(H/m)，ε=8.85×10-12(F/m)，有|ωε|≪γ，则jωμ(γ+jωμ)≈jωμγ，代入式(2)化简，又有ω=2πf和B=μH，则

2H=2πjfμγH

(3)

图3为单层铜箔，其中铜箔的宽度和厚度分别用w和h表示，且w远大于h，y为电流方向。

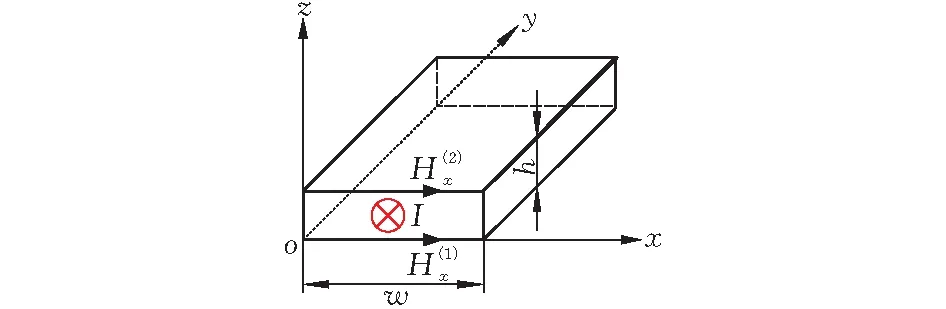
图 3 平面变压器单层铜箔示意图

由式(3)可得：

2Hx(z)=2πjfμγHx(z)=(1+j)2πfμγHx(z)

(4)

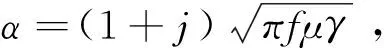
2Hx(z)=α2Hx(z)

根据边界条件Hx(z=0)=Hx(1)，Hx(z=h)=Hx(2)求解后代入电磁场关系Jy(z)=-∂Hy(z)/∂z得铜箔内的电流密度分布

Jy(z)=

则单位长度铜箔的功率损耗

其中，n=h/Δ，即把导体厚度表示为n个趋肤深度。根据一维条件下导体的趋肤效应和邻近效应的正交性，则绕组功率损耗还可表示为式(5)与(6)的和，Ps为导体的趋肤效应损耗，Pp为邻近效应损耗。

(5)

(6)

1.3 平面变压器初、次级绕组交叉排列对损耗的影响分析

如图4所示，匝比为2∶1的平面变压器，初级绕组为两层绕组串联，次级为一层绕组，绕组分别为图4a绕组无交叉排布和图4b初、次级绕组交叉排布两种绕组排布方式，绕组宽度均为w，绕组厚度均为h，初级电流为I1，次级电流为I2，方向相反，则2I1=-I2。

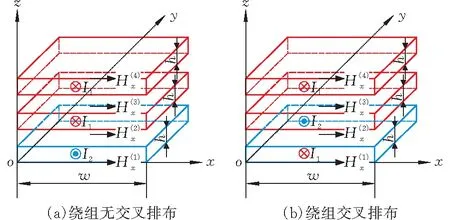
图 4 平面变压器绕组结构示意图

根据安培环路定理可得绕组无交叉排布单位长度的损耗

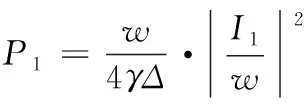
(7)

根据上述方法，求得绕组交叉排布单位长度的损耗

(8)

对比式(7)和式(8)可知：两种排布方式的趋肤效应损耗完全一致，但初、次级绕组交叉排布时的邻近效应损耗远小于绕组无交叉时的损耗。因为绕组交叉排布时初级电流在次级产生的磁场强度大小相等且方向相反，故可以相互抵消，采用交叉换位技术对绕组进行排布，减小绕组损耗的效果明显。

2 平面变压器次级绕组电流均分

通过前面的分析可知，采用初、次级交叉排布的方式能够减小绕组的损耗，但当平面变压器次级绕组并联层数过多时，由于相邻绕组间磁场的相互作用，各并联绕组中的电流可能会分布不均，导致平面变压器的绕组损耗增加。如何合理地布置绕组，使并联绕组电流均分，是平面变压器结构设计的一个关键问题。

2.1 平面变压器次级单绕组多层并联的布置方法

图5是一个匝比为2∶1的平面变压器绕组结构示意图，红色(深色)为2匝绕组串联构成的2匝初级绕组，蓝色(浅色)为2匝绕组并联构成的1匝次级绕组，保持初、次级绕组宽度及高度一致。

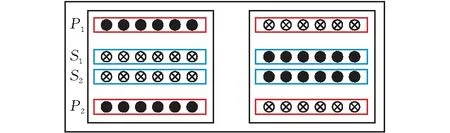
图 5 匝比为2∶1的4层绕组平面变压器结构示意图

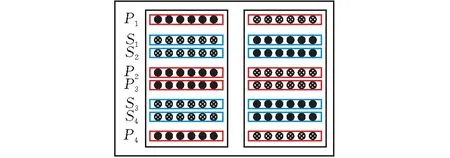
图 6 匝比为4∶1的8层绕组平面变压器结构示意图

根据绕组结构的对称性，并联绕组中的电流也是相同的，将图5中的绕组分别作为8层绕组布置的上、下两部分，得到如图6所示匝比为4∶1的平面变压器。其中，初、次级分别有4层绕组，每层绕组为1匝，初级绕组串联构成4匝，次级绕组并联构成1匝，初、次级绕组宽度及高度一致。根据绕组结构的对称性可知，绕组S1和S4中的电流相等，绕组S2和绕组S3中的电流相等，因绕组S1和S2中的电流相等，故次级各并联绕组实现电流均分。由此可以推论，以匝比为2：1的平面变压器的绕组布置方法为基础，可以实现2n层(n为大于1的正整数)的绕组布置方法，使电流在次级并联绕组中分布一致。

在理想变压器中，有：

NPIP=NSIS

其中，NP和NS分别为变压器的初级和次级绕组匝数，IP和IS分别为变压器的初级和次级绕组电流。在图6中，次级绕组电流是初级绕组电流的4倍。

绕组P4、S4中的电流大小相等，方向相反，故去掉绕组P4、S4后，并联绕组S1、S2、S3中的交流电阻保持不变，得到如图7所示的匝比为3∶1的6层绕组平面变压器结构示意图。

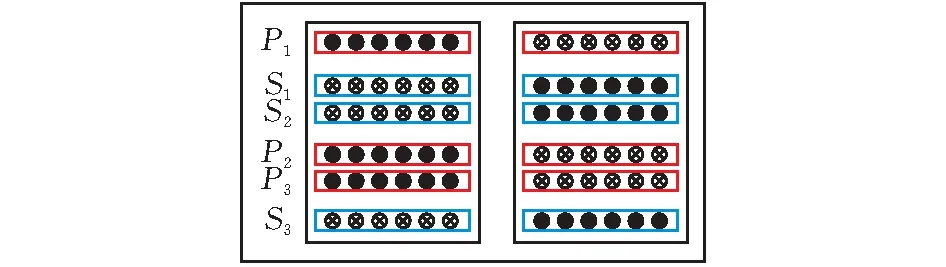
图 7 匝比为3∶1的6层绕组平面变压器结构示意图

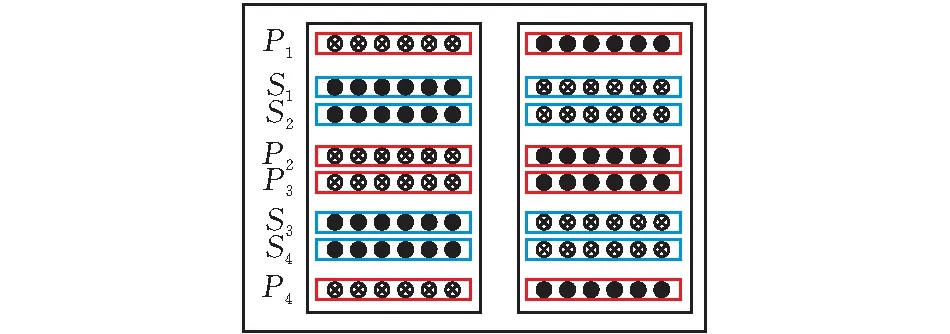
图 8 匝比为4∶1的8层绕组平面变压器结构示意图

同时，进一步可得到如图8所示的匝比为4∶1的平面变压器绕组结构示意图，且并联绕组中的电流一致。以此推广，可以实现绕组为2n层(n为大于1的正整数)匝数比为n∶1的绕组对称布置方法使电流在次级并联绕组中分布一致。

2.2 平面变压器次级多绕组多层并联的布置方法

为了实现高频开关电源的多路输出功能，在设计平面变压器时次级绕组的个数不止一个，次级各绕组同时工作时工作绕组电流可能存在差异，此时会相应地产生涡流损耗。

图9中，N1为初级匝数，电流为i1，N2、N3、N4、N5分别为次级绕组匝数，绕组电流分别为i2、i3、i4、i5，次级绕组同时工作。

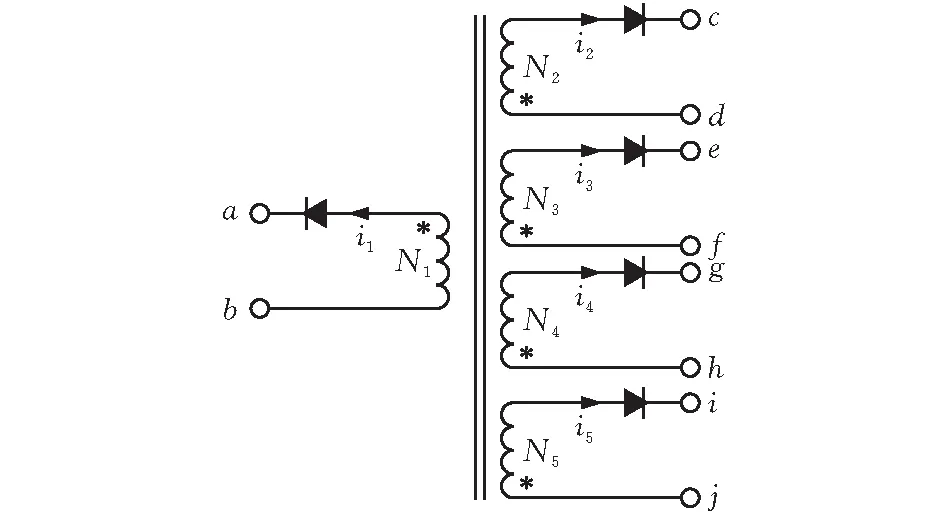
图 9 次级多绕组的反激变压器结构图

令N2=N3=N4=N5=1，在上面分析中，得出了次级单绕组多层并联电流均分的布置方法，对于次级多绕组平面变压器，可将其等效为次级单绕组多层并联，区别在于各层的连接方式不同，将初级的匝数设为4匝，即N1=4，根据上述次级单绕组多层并联的布置方法，可得如图10所示的两种绕组电流均分布置结构。

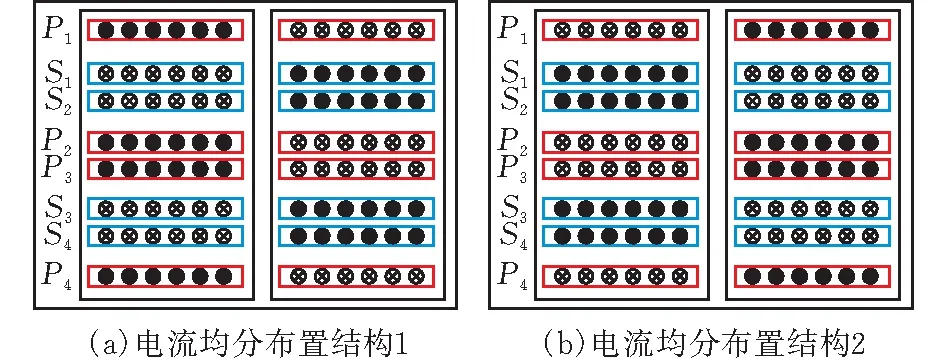
图10 次级多绕组电流均分布置结构示意图

3 仿真验证

3.1 平面变压器初、次级绕组交叉排列对损耗的影响

建立如图11所示的匝比为2∶1的交叉绕组平面变压器模型，初级绕组为2层绕组串联，次级绕组为单层绕组，绕组厚度均为0.035 mm，采用飞磁公司的ER14.5/3/7磁芯，气隙为0.01 mm，绕组内径为3.15 mm，宽度为2 mm，各层绝缘厚度为0.1 mm，绕组间采用空气绝缘，磁导率为4π×10-7H/m，介电常数为8.85×10-7F/m，激励源为电流源，原边绕组通过幅值为10 A的正弦交流电，副边绕组通过幅值为20 A的正弦交流电，电流源频率分别为1～10 MHz。选择瞬态场求解器对绕组涡流损耗进行解析，得到交叉绕组平面变压器绕组涡流损耗。结合无交叉绕组平面变压器涡流损耗得如表1所示的不同绕组结构的平面变压器涡流损耗。

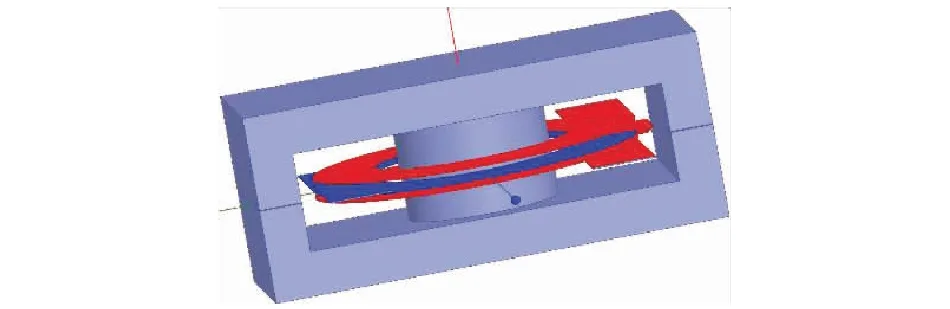
图11 匝比为2∶1的交叉绕组平面变压器模型

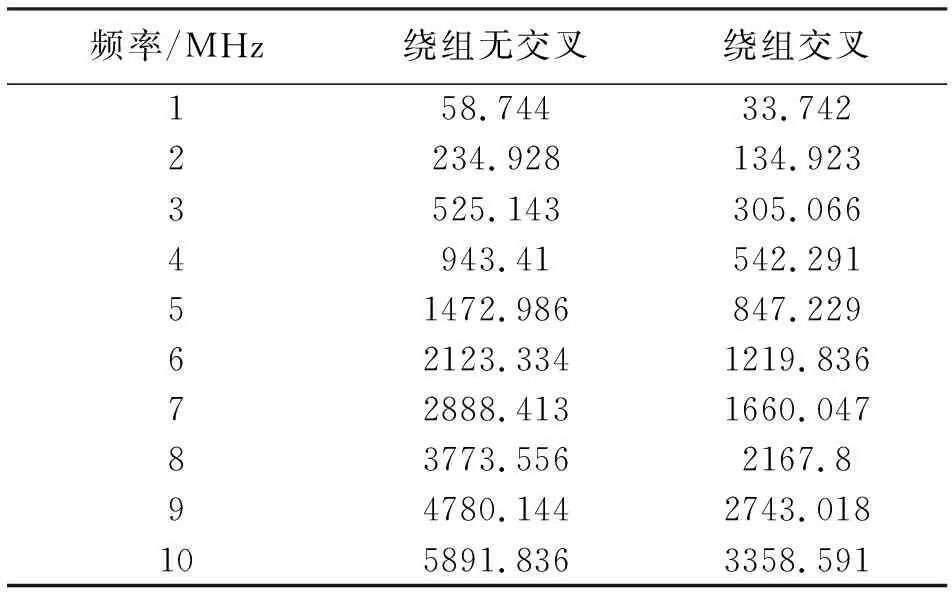
表1 不同绕组结构的平面变压器涡流损耗

由图12可知，当初、次级绕组交叉排布时能够大大减小平面变压器的涡流损耗，且工作频率越高，绕组交叉排列减小损耗的效果越明显，因此，在设计平面变压器时，初、次级绕组应采用交叉绕组结构，以减小由于高频效应产生的邻近效应损耗。

图12 不同绕组结构的平面变压器涡流损耗随工作频率的变化曲线

3.2 平面变压器并联绕组均流布置方法的仿真验证

根据上文分析，建立如图13所示的匝比为2∶1的交叉绕组平面变压器的两种绕组结构模型，初级绕组为2层绕组串联，每层1匝，次级绕组为2层绕组并联，每层1匝。初、次级绕组为铜箔，绕组厚度均为0.035 mm，其他条件与上节相同。选择静磁场求解器(magnetostatic magnetic)，边界条件为气体边界条件，在原边副边均给激励电流源，初级电流为10 A，次级电流20 A，处理可得到如图14所示的两种绕组结构的绕组电流密度分布图，可知两种绕组结构都可以实现次级并联绕组电流均分。

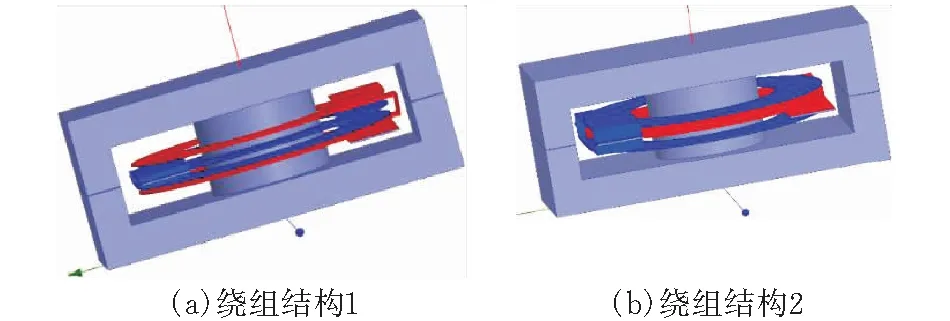
图13 匝比为2∶1的交叉绕组平面变压器模型

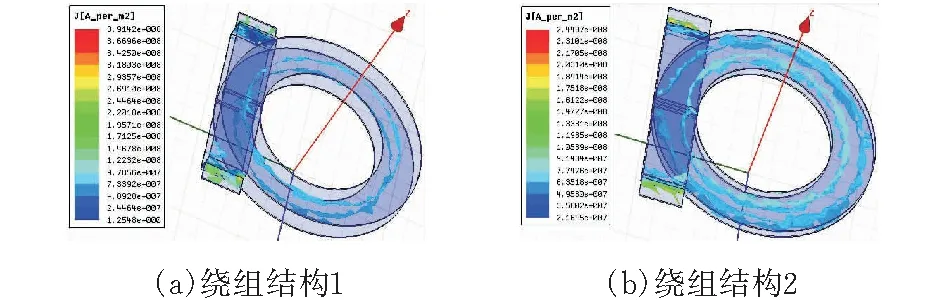
图14 次级并联绕组电流密度分布

建立如图15所示的匝比为4∶1的交叉绕组平面变压器模型，变压器初级由4层绕组串联组成，每层为一匝，次级由4层绕组并联组成，每层为一匝，激励源为电流源，初级电流为10 A，次级电流40 A，对应的次级并联绕组电流密度分布见图16，可知次级并联绕组电流均分。

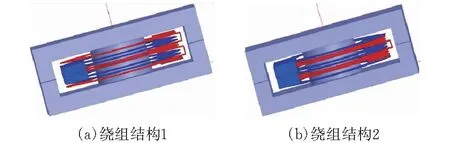
图15 匝比为4∶1的交叉绕组平面变压器模型

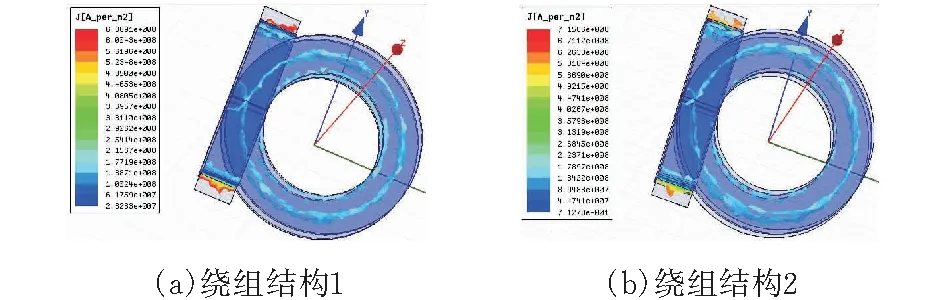
图16 次级并联绕组电流密度分布

建立如图17所示的匝比为3∶1的交叉绕组平面变压器模型，变压器初级由3层绕组串联组成，每层为1匝，次级由3层绕组并联组成，每层为1匝，激励源为电流源，初级电流为10 A，次级电流30 A，次级并联绕组电流密度分布图如图18所示，可知次级并联绕组电流均分。

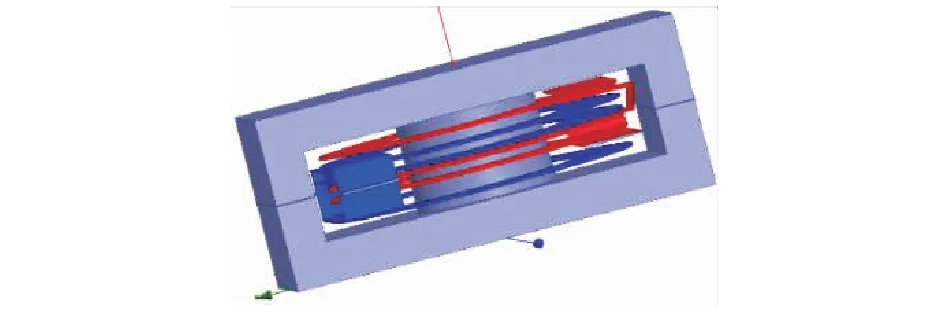
图17 匝比为3∶1的交叉绕组平面变压器模型

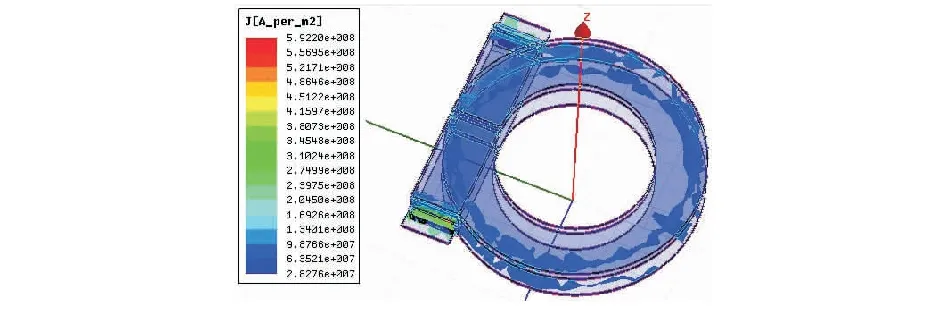
图18 次级并联绕组电流密度分布

建立如图19所示的匝比为4∶1∶1∶1∶1的交叉绕组平面变压器模型，变压器初级由4层绕组串联组成，每层为1匝，次级为4组绕组结构，每组为1匝，激励源为电流源，初级电流为10 A，次级电流均为10 A。次级绕组电流密度分布图如图20所示，可知次级绕组电流均分。

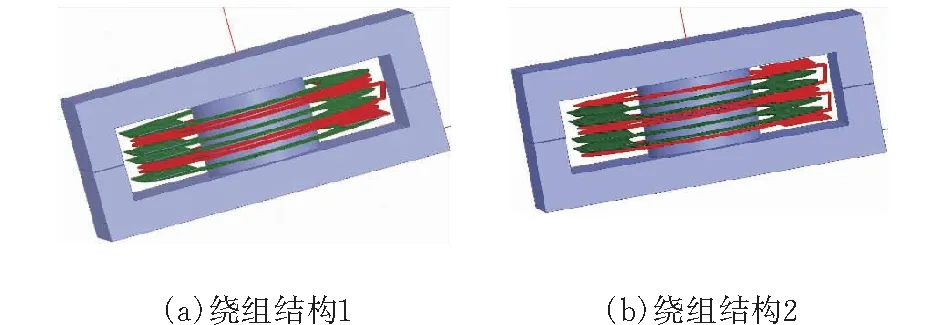
图19 匝比为4∶1∶1∶1∶1的交叉绕组平面变压器模型

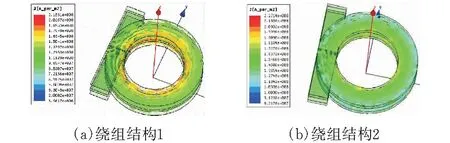
图20 次级并联绕组电流密度分布

4 总结

本文针对平面变压器中高频损耗的问题，利用一维条件下趋肤效应与邻近效应的正交性，推导出将初、次级绕组采用交叉换位技术能够有效减小绕组损耗。针对次级并联绕组电流分布不均的问题，根据平面变压器绕组结构的对称性以及并联绕组电流的关系，推导出了平面变压器电流均分的n∶1绕组布置方法。最终通过Maxwell电磁场分析软件验证了绕组电流均分的可行性。