热探针法测试颗粒多孔材料有效热导率的研究
马爱纯,蔡澄汉,周天,李力
(中南大学能源科学与工程学院,湖南长沙,410083)
碳化硅、石英砂与工程砂不仅可作为原料广泛应用于建筑、陶瓷、化工等行业,而且还是多种复合材料的基料,对其有效热导率进行研究可以为功能陶瓷的成型与性能改进、建筑保温材料的优化设计等提供重要参考。受颗粒热导率、颗粒间气相和(或)液相含量、粒径等因素影响,颗粒多孔材料的有效热导率难以通过理论计算得到,通过实验测量可以获取较准确的有效热导率。目前,适用于颗粒多孔材料有效热导率实验测试的方法主要有稳态防护热板法[1−2]、非稳态热线法[3−6]、热带法[7−9]及热探针法。防护热板法基于稳态导热,要求装置和试样达到热稳定后才能进行测试,故耗时较长[10]。热线法与热带法测试时间较短,可对砂土[4]、粉煤灰[4]、二氧化硅气凝胶[3,7−9]、水泥珍珠岩[4]和土壤[4,6]等颗粒多孔材料有效热导率进行有效地测量,但实验对测试环境与试样定型要求较高,易产生较大的系统误差。热探针结构坚固,整体测试装置简单,可从多方位对散体材料有效热导率进行测试。此外,热探针法耗时较短,对试样加工定型要求较低,且不易受环境变化影响,可应用于实地测试工作。人们对采用热探针法获取不同颗粒多孔材料有效热导率开展了较多研究[11−18],如:刘路路等[11]研究了不同含砂率、含水率及干密度对橡胶−砂颗粒混合物热导率的影响,发现试样的热导率均随含砂率与干密度的增大而增大,随含水率的增大先增大后趋于稳定;徐国稳等[12]采用热探针法测试了石英砂颗粒的有效热导率,并将实验结果与数值计算结果进行比较,发现孔隙率是影响干试样有效热导率的主要因素之一;张心怡等[13]研究了微细树脂颗粒在离子交换条件下,其有效热导率随粒径、孔隙率、流速的变化,发现热探针法的应用不受颗粒间是否发生离子变化影响。对于土壤类颗粒多孔材料,热探针法可用于研究其有效热导率随温度、含水率、干密度或孔隙率的变化规律[14−18]。可见,热探针法非常适合于获取颗粒多孔材料的有效热导率,但目前人们对孔隙率、含水率及粒径等多因素对颗粒多孔材料有效热导率的耦合影响研究较少。本文作者采用热探针法测试碳化硅、石英砂和工程砂颗粒在干燥(两相)及含湿(三相)状态下的有效热导率,研究孔隙率、含水率及粒径对其影响,并得到相关的拟合关系式。
1 测试原理
热探针法基于半无限大非稳态导热模型,其热流传导如图1所示。将1根功率恒定的热探针插入待测试样中,其表面温升速率受到试样热导率等因素影响,通过记录热探针温度随时间的变化规律,可以计算试样热导率。

图1 热探针法热流传导图Fig.1 Heat transfer diagram of thermal probe
假定试样具有颗粒分布均匀、尺寸无限大,且具有均匀稳定的初始温度;热探针无限长、热容量忽略不计,且初始温度均匀。可得到热探针壁面温升随时间变化的级数展开式[19]:

式中:下标μ,h 和a 分别表示试样、加热丝与空气;r0为热探针半径,m;τ为加热时间,s;T(r0,τ)为热探针表面在τ时刻的温度,K;T0为热探针的初始温度,K;θ为热探针表面的过余温度,K;q为单位长度加热功率,W/m;λμ为试样热导率,W/(m·K);αμ为试样热扩散率,m2/s;lnC=0.577 216,为欧拉常数;ϖ=2ρμcp,μ/(ρhcp,h);ρμ与ρh分别为试样和加热丝的密度,kg/m3;cp,μ与cp,h分别为试样和加热丝比热容,J/(kg·K);R=εh/(λar0),为单位长热探针与试样的接触热阻,(m·K)/W;εh为热探针与试样之间的接触间隙,m,λa为空气热导率,W/(m·K);L为级数展开式的余项和。
当r0足够小、τ足够大时,r0/(4αμτ)趋于0,忽略高阶小量,则式(1)可简化为

式中:e=q/(4πλμ);f=e·ln[4αμ/(r02C)]。
由式(2)可知,θ与lnτ呈线性关系。利用最小二乘法在有效时间段内进行线性拟合,可得θ−lnτ关系曲线的斜率e,进而计算出λμ:

在实验初期τ较小,r0/(4αμτ)不趋于0,忽略式(1)中高阶项会引起较大的截断误差;当测试时间过长时,热探针产生的热流会传递到试样边缘而与外界发生热交换,与半无限大非稳态导热模型相矛盾,两者均导致θ−lnτ曲线的线性变差。有效时间段是指在θ−lnτ曲线上开始进入线性时刻到开始偏离线性时刻之间的时间段。
2 实验系统设计
2.1 实验装置
测试系统由热探针、恒温槽、电源和数据采集装置组成,如图2所示。实验时,首先将待测试样装入底部密封的PVC 硬质管中,在待测试样中插入热探针后将PVC 硬质管置于恒温水浴中。待测试样在恒温水浴中达到热平衡后,在热探针加热丝两端加恒定电压。将热电偶测得的热探针温度通过无纸记录仪传输到计算机并进行数据处理,最终计算试样热导率。

图2 热探针法测试系统Fig.2 Thermal probe testing system
热探针作为测试系统的核心部件既是加热元件,又是测温元件。当热探针长径比大于25 时可大幅度降低轴向热损失引起的误差。实验采用外径为2.0 mm、内径为1.7 mm、长度为17.0 cm的不锈钢管作为套管,用导热硅脂填充,并在两端用环氧树脂均匀胶封,防止水分进入热探针内部。加热丝选用直径为0.13 mm的漆包镍铬丝,绕制14匝,单匝长28 cm。热探针结构如图3所示。
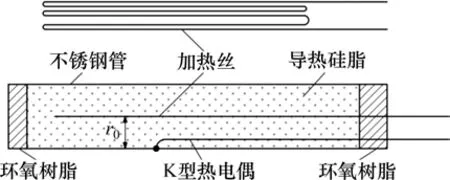
图3 热探针结构示意图Fig.3 Diagram of thermal probe structure
2.2 实验材料制备
实验材料为不同孔隙率、含水率及粒径的碳化硅、石英砂和工程砂颗粒。碳化硅的粒径分别为75,103,180,335 与700 μm,石英砂的粒径分 别 为75,[86,150],[180,425),[425,850)与[850,2 000]μm,工程砂的粒径分别为[150,250),[250,300),[300,425),[425,850)与[850,2 000]μm。针对每种粒径的试样,分别制备5种不同孔隙率和含水率的待测样品。
2.2.1 孔隙率测定与制备
实验采用密度法,通过测定试样的堆积密度ρη和表观密度ρg计算得出孔隙率n,其计算公式为

测定表观密度时,首先用恒温烘箱将待测试样烘干至恒质量,冷却后称100 g试样放入装有蒸馏水的李氏瓶中。预先将蒸馏水凹液面与1 mL 刻度线平齐。静置恒温至20 ℃后读取李氏瓶的刻度,其计算公式为
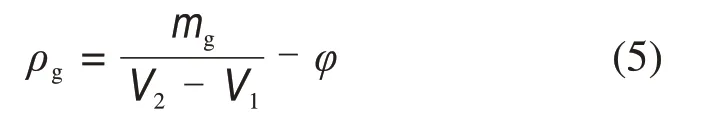
式中:mg为试样质量,g;V1为李氏瓶初始刻度对应体积,mL;V2为试样静置至20 ℃时的刻度对应体积,mL;φ为水温对水密度影响的修正系数,20 ℃时为0.005。
测定堆积密度时,首先将烘干后的待测试样放入质量为m1的空物料桶中,抚去物料桶顶部多余的试样,直至试样与内壁刻痕平齐,并记录下总质量m2,其计算公式为

式中:m1为空物料桶质量,kg;m2为试样与物料桶总质量,kg;Vh为物料桶容积,m3。
不同孔隙率的多孔材料可通过施加不同的压力来改变堆积密度制备。为保证试样孔隙率分布均匀,采用匀速正向与反向加载的方式制备不同孔隙率的试样[20]。
2.2.2 含水率测定与制备
采用质量含水率作为分析指标,首先在恒温烘箱中将待测试样烘干至恒重并称其堆积质量,然后使用小型喷雾器将所需用水量多次均匀喷入待测试样中,分别制备出含水率为0,5%,10%,15%和20%共5种待测试样。为保证试样含水率均匀分布,将试样装入PVC 试样管后用防水膜密封并盖上EPS盖分别正立和倒立6 h[20]。
2.3 实验装置标定
为验证实验装置的可靠性,实验前选用热导率已知的甘油作为标准物质对实验装置进行标定。将热探针插入装有甘油的试样管后一同放入恒温水槽中。待甘油整体温度均匀稳定后,对热探针施加不同的加热功率,并在有效时间段即10~240 s内重复测量3 次取平均值。实验数据中存在对θ−lnτ曲线拟合质量无益的数据点,采用基于斜率相对标准差的数据筛选法[21]剔除无效数据点,保留有效数据点,以便更精确地求出待测试样的有效热导率。
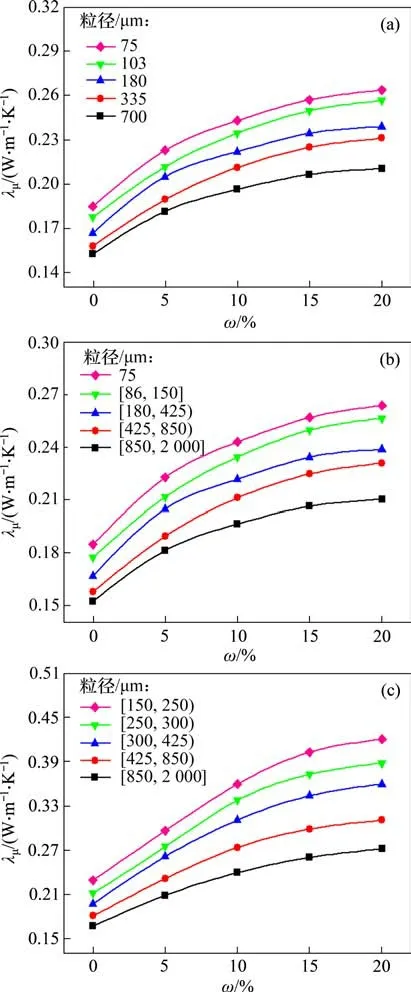
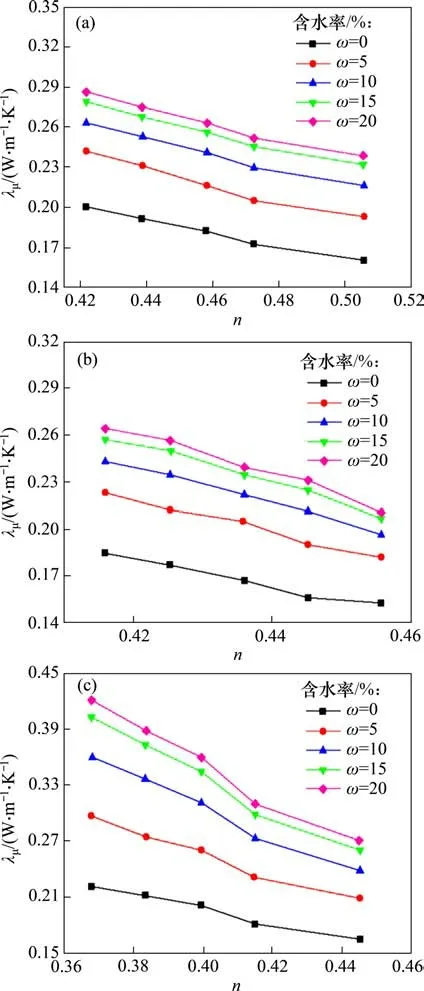
实验测得热导率如表1所示。根据文献[22]给出的标准甘油在温度6.85~106.85 ℃时的热导率测试结果,按线性插值估算出甘油在24.5~26.5 ℃内的热导率,发现甘油热导率随温度变化较小,偏差仅为0.1%。因此,取甘油在25.5 ℃时的热导率0.287 8 W·m−1·K−1作为参考值,计算各热导率测试值相对参考值的残差与误差,并进行误差分析。经计算得测试均值-x=0.287 3,标准差s=0.002 55。根据格拉布准则,当样本数为5个、显著性水平为0.005 时,格拉布临界值g0.005(5)=1.764,最大统计量g5=1.295 3.1.1 孔隙率及粒径对颗粒多孔材料有效热导率的影响 图4所示为不同粒径下孔隙率n对颗粒多孔材料有效热导率λμ的影响。从图4可以看出3 种颗粒多孔材料在不同粒径范围其有效热导率均随孔隙率增加而减小,这是因为两相颗粒多孔材料的有效热导率由固相和气相共同决定。一方面,随孔隙率n增大,空气占比增加,而空气热导率远小于固相物质热导率,所以,有效热导率随之减小;另一方面,孔隙率增大也造成颗粒间接触热阻增大,导致有效热导率减小。 表1 标准甘油热导率测量结果Table 1 Thermal conductivities of standard glycerol 图4 有效热导率λμ随孔隙率n变化规律Fig.4 Variation of effective thermal conductivity with porosity 此外,当碳化硅、石英砂、工程砂这3种材料的粒径范围分别在75~180,75~425 和150~425 μm 时,其孔隙率存在重合区间,分别为0.393 6~0.458 1,0.399 9~0.445 2 和0.364 0~0.399 6。在孔隙率重合区间内,这3种材料相同孔隙率不同粒径间有效热导率基本相同,最大偏差分别为1.0%,0.7%和0.6%。粒径对这3种颗粒多孔材料有效热导率的影响均较小。 3.1.2 两相颗粒预测模型 不考虑粒径影响,对碳化硅、石英砂、工程砂这3 种材料有效热导率实测值进行多项式拟合,得到两相颗粒多孔材料有效热导率与孔隙率的预测式,分别见式(7),(8)和(9)。图5所示为这3 种材料有效热导率预测结果与实测结果的对比。从图5可见:这3种材料有效热导率预测结果与实测结果相对误差均在3%之内,拟合优度分别为0.993 8,0.988 8与0.987 4。 图5 有效热导率λμ预测值与实测值对比Fig.5 Comparisons between predicted and measured values of effective thermal conductivity 3.2.1 含水率对颗粒多孔材料有效热导率的影响 图6 有效热导率λμ随含水率ω变化规律Fig.6 Variation of effective thermal conductivity with moisture content 在不同粒径下,碳化硅、石英砂、工程砂这3种颗粒多孔材料有效热导率随含水率ω的变化见图6。从图6可以看出:随含水率增大,这3 种材料在不同粒径下的有效热导率均不断增加,增幅开始较大,之后逐渐减小。这是因为水的热导率(0.599 W·m−1·K−1)约为空气的23 倍,随含水率增大,液相组分相对增加而气相组分相对减少,颗粒间形成液桥,使材料整体导热能力增强;当含水率超过15%时,颗粒间液桥数量趋于饱和,此时,有效热导率增速趋缓。 3.2.2 孔隙率对颗粒多孔材料有效热导率的影响 图7 有效热导率λμ随孔隙率n变化规律Fig.7 Variation of effective thermal conductivity with porosity 在不同含水率下,这3种颗粒多孔材料有效热导率随孔隙率的变化见图7。从图7可以看出:随孔隙率增大,这3 种材料有效热导率均不断减小;当碳化硅与工程砂颗粒的孔隙率分别增大至0.480与0.415时,空气占比的增加对材料整体导热性能的影响逐渐变弱,有效热导率降幅逐渐变小;当含水率小于等于5%时,石英砂颗粒有效热导率随孔隙率增大开始快速减小,当孔隙率大于0.445时,降幅逐渐变小,但当含水率为10%~20%时,降幅仍较大。这是因为随孔隙率增加,单位体积内空气占比增大,致使材料整体导热性能下降,但当孔隙率达到某个值时,空气占比增加对整个有效热导率的影响会逐渐减小。但对于本实验中含水率较大的石英砂颗粒,还未找到空气占比影响变小的拐点。 3.2.3 三相颗粒预测模型 碳化硅、石英砂和工程砂颗粒的三相有效热导率与含水率、孔隙率的预测关系式分别见式(10),(11)和(12),这3个预测式所得有效热导率的误差分别在5.2%,3.0%与5.0%之内,拟合优度分别为0.983 3,0.993 5与0.991 0。 1)孔隙率是决定颗粒多孔材料两相有效热导率的主要因素,颗粒多孔材料的两相有效热导率均随孔隙率增加而显著减小,粒径产生的影响可忽略。 2)颗粒多孔材料的三相有效热导率均随含水率增加而增大,但当含水率超过15%时增速趋缓;随孔隙率增加而减小,当孔隙率增大至一定程度时,降幅逐渐减小。这说明含水率与孔隙率对颗粒多孔材料三相有效热导率的影响均存在相应的饱和值。但对于本实验中含水率较大的石英砂颗粒,还未得到有效热导率降幅逐渐减小的拐点。 3)得到3种颗粒多孔材料的两相、三相有效热导率预测式,其中两相预测式所得有效热导率误差在3%以内,三相预测式所得有效热导率误差在5.2%以内。针对具有不同粒径、孔隙率和含水率的颗粒多孔材料,热探针法可用于测试其有效热导率,并可推广到类似硬质颗粒多孔材料的有效热导率测试。3 结果与讨论
3.1 两相颗粒多孔材料





3.2 三相颗粒多孔材料

4 结论

