含风电的综合能源系统源-荷滚动优化调度模型

郑志杰， 吴奎华， 綦陆杰， 王延朔， 梁 荣， 李 凯

(国网山东省电力公司经济技术研究院, 山东济南250001)

近年来，风电接入[1-2]的综合能源系统[3]已引起国内外学者的关注。系统消纳风电水平受限是风力发电快速发展过程中面临的主要问题，其结果是导致严重的弃风弃电现象[4]，进而使得综合能源系统运行成本提高[5]。同时，当冷热负荷需求较大且燃气机组无法满足用户需求时， 综合能源系统会利用电驱动设备补偿冷热负荷缺额，导致白天电负荷需求增加， 进一步拉大了负荷曲线的峰谷差，因此，促进风电消纳和减小负荷曲线峰谷差是综合能源系统亟需解决的2个问题。

上述问题出现的原因主要有2个：一是风电的反调峰特性[6]，即在负荷低谷时段风电出力较高，负荷高峰时段风电出力较低；二是风电具有随机波动性，现有的风电预测方法无法随时保证高精度，经常出现风电预测误差。国内外学者针对上述问题进行了广泛研究。文献[7]中在优化调度模型中加入了空调负荷，并将空调负荷视为需求响应资源，使得负荷曲线更平滑，但该需求响应模型只涉及一种资源。文献[8]中对多种柔性负荷进行建模，通过供需端的优化调度实现系统的经济合理运行，但没有考虑用户满意度。文献[9]中将分布式能源的不确定性加入到需求响应中，提高了电源侧与负荷侧的互动性，但没有涉及需求响应中负荷转移的衰减效应，导致最后的仿真结果偏离实际情况。在风电出力的随机波动特性分析方面，文献[10]中考虑风电预测误差满足的正态分布函数，将风电出力的不确定性转化为预测误差的不确定性，增加了风电预测值的准确度，并建立了风电调度模型。文献[11-12]中利用场景分析法对可再生能源出力进行建模，将风电出力固定值转化为一系列概率值，减弱了风电不确定性对风电消纳的影响。以上文献中系统的调度模型均基于供电侧或负荷侧，一般只调度单侧资源，风电的消纳水平仍然有限。

为了有效提升综合能源系统对风电的消纳能力和减少负荷峰谷差，并改善系统的经济性，本文中提出含风电的综合能源系统源-荷滚动优化调度方法。首先，以综合能源系统的框架为基础，分析需求响应与风电消纳的关系；其次，通过引入负荷的衰落效应[13]，构建柔性负荷需求响应模型，并采用场景分析法处理风电出力及需求响应模型中参数的不确定性；最后，以综合能源系统运行成本最小为目标，利用滚动优化的方法求解系统运行策略。

1 风电消纳机理

1.1 综合能源系统结构

综合能源系统是涵盖供冷、供热、供电的综合性供能平台，集成了多种形式的供能、能量转换和储能设备，在源、网、荷等不同环节实现不同类型能源的耦合。该系统主要由燃气轮机、燃气锅炉、吸收式制冷机、电制冷机以及分布式电源等设备构成，如图1所示。本文中仅考虑风力发电一种分布式电源。

图1 综合能源系统结构图

1.2 机理分析

风电具有明显的反调峰特性，即风电在白天用电高峰期出力较小，此时风电可以被系统完全消纳，而在晚上用电低峰期风电出力较大，此时，综合能源系统在没有任何措施的情况下不能完全消纳风电，从而导致弃风现象。本文中采用源-荷协调的优化方法，在晚间风电出力较大时，利用需求响应将部分负荷转移到该时段，同时降低系统发电机组的出力，提高系统风力消纳的能力，减少综合能源系统的弃风量。上述协调过程如图2所示。

图2 源-荷协调互动原理

2 需求响应与场景生成

2.1 考虑衰减效应的电负荷需求响应

用户参与需求响应遵循自愿原则，利用需求弹性系数表示用户对电价的响应程度。需求弹性系数通常通过对历史分时电价机制下的用户电量进行统计分析获知。计及需求弹性系数后的实时负荷需求计算公式为

(1)

用电量的减少不利于公共事业的利益。为了弥补需求响应对公共事业造成的损失，用户会有意识地增加其他时段的需求，这种现象称为负荷恢复。负荷恢复通常利用需求回收率建立模型，均匀分布在负荷减少的时间段内。由于负荷本身的属性，用户满意度在需求响应前达到最大值，随着等待时间的延长，用户满意度逐渐降低，因此，在需求响应建模中必须考虑衰减效应，才能进行准确地仿真分析。根据控制策略的不同，需求响应中总回收率计算公式为

(2)

式中：Pcov(t,t′)为恢复区间[t,t′]内的负荷恢复量，t′为恢复区间内的时刻；υ为需求恢复量与减少量的比值，υ≥1；T为恢复过程的持续时间；rt为t时刻的负荷衰减系数。

衰减效应的影响使得Pcov(t,t′)不是常数，而是一个时间变量。假设需求随时间线性恢复，恢复速率为ϖ，表示需求恢复随时间递减的程度。用户进行需求响应时，不仅可以选择延迟用电，也可以提前调度用电，因此恢复区间的需求回收量用对称的分段函数表示，即

(3)

将式(1)—(3)结合，得到综合负荷需求的表达式为

(4)

式中：D(t)为t时刻的综合负荷；Dure(t)为时刻t的刚性负荷；Tr为恢复区间内的时刻的集合。

2.2 热负荷需求响应模型

热负荷主要包括供暖和热水，本文中以供暖为主建立热负荷模型。由于用户对供热舒适度的感知具有一定的模糊性，在一定范围内改变温度值对用户并没有太大影响，因此可以在保证用户舒适的区间内，通过调节供暖温度来降低热负荷量。在保证用户温度舒适区间内对温度进行适度的调节，可实现调度负荷需求的目标。考虑到热负荷具有一定的时间延续性，改变供热温度后建筑物的温度不会立即发生突变，即热负荷的计算模型是非线性的，即

Htload=VS(Ttn-Ttw)-(Tt-1n-Tt-1w)exp-Δtτ ,ΔHtload=f(Ttn)-f(Ttn-Δt) , (5)

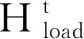
冷负荷需求响应模型与该模型机理相同，不再赘述。

2.3 综合场景生成

式(4)的输出结果是理想情境下的需求；但是，由于设备组成和其他不可预测因素的影响，用户对实时电价的响应程度在现实中存在很大差异，因此很难得到所有用户准确的需求曲线。此外，用户是否愿意透露他们的用电隐私也存在疑问。这些不确定性使得参数ε(t)、υ、ϖ具有很强的随机性。

对于包含大量独立负荷的配电系统，特别是在中压水平，需求响应的聚集形式表现出统计规律性。一些先进的预测技术可以用来估计与价格响应相关的参数的概率密度函数。通常认为ε(t)服从高斯分布[14]，考虑到需求弹性系数有上、下限的约束，ε(t)的概率密度函数表示为

g[ε(t)]=

(6)

式中:εmin(t)、εmax(t)分别为需求弹性系数取值的最大和最小值；μ(t)、σ(t)分别为需求弹性系数正态分布中的均值和标准差。

υ均匀分布在区间[1,υmax]，ϖ均匀分布在区间[1,ϖmax]，υmax、ϖmax分别为υ、ϖ的上限。

本文中主要考虑风电、需求弹性系数、需求恢复量3种不确定性因素，设计每个场景表征系统可能出现的运行状态。将上述不确定性综合成一组场景[15]，纳入规划模型，即

(7)

采用拉丁超立方抽样方法生成场景，初始场景数量较大，为了减少计算量，利用同步回代削减法[16]缩减其数量。总场景n为风电、需求弹性系数与需求恢复量的随机组合，即

n=nwinnεncov，

(8)

式中nwin、nε、ncov分别为风电、需求弹性系数、需求恢复量样本个数。

3 考虑风电消纳的综合能源系统滚动优化模型

在k时刻将得到的混合场景带入优化模型，滚动优化得到未来M时域内的控制输入序列，但只实现k+1时间区间的调度。在下一个优化时段，M向后移动一个时间区间Δt，这就是滚动优化[17]的思想。再次根据最新信息进行优化，滚动优化模型的时间窗口如图3所示。

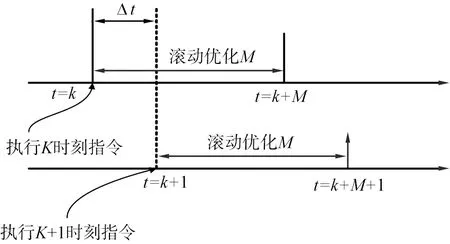
Δt—2次指令之间的时间间隔； K—执行指令的时刻；t—时间变量； M—滚动优化的时长。

需求侧的负荷曲线是进行电力系统优化调度的依据。本文中考虑负荷需求响应机制，加入符合用户消费心理的衰减效应，使得需求响应后的负荷曲线更接近实际情况。风电出力具有明显反映调峰特性，需求响应的削峰填谷作用恰好改善了风机的弃风弃电现象[18]。

风电机组比燃煤机组发电成本小，但受风电不稳定性的影响，风电机组大规模并网会造成系统原有机组被迫参与大规模调峰调频工作，增加电力系统调度成本[19]，因此，为了提高综合能源系统的风电消纳能力，同时满足经济性要求，本文中以系统运行成本C0期望值E(C0)最小为目标函数。

3.1 目标函数

(9)

(10)

(11)

(12)

3.2 约束条件

1)功率平衡约束。

(13)

式中：Ui,s,t为机组i在场景s下t时刻的状态变量；θi、θw分别为机组i和风电场的厂用电率。

2)旋转备用约束。

(14)

(15)

(16)

(17)

3)设备出力约束。

gw,s,t≤λtgw，

(18)

(19)

式中：gw,s,t为风电在t时刻场景s下的出力；λt为t时刻风电最大等效利用系数；gw为风电总装机容量。

4)机组爬坡约束。

(20)

式中gi,s,t-1为机组i在t-1时刻场景s下的出力。

5)最短启停时间约束。

(21)

(22)

综合考虑用户需求响应和风电出力的不确定性，提出区域级综合能源的源-荷联合滚动优化模型。优化步骤如下：

1)利用风电出力、需求弹性系数、需求恢复量的历史数据预测得到未来特定时域M内的预测值；

2)对各单元预测误差服从的概率分布函数运用拉丁超立方抽样生成初始场景集，并采用同步回代削减法缩减场景数量直至满足设定场景数；

4)根据滚动优化出的粒子的适应度值，对粒子的个体最优位置和全局最优位置进行更新；

5)更新第1层优化中各粒子的位置和速度；

6)将实际的风电、需求弹性系数、需求恢复量反馈到预测模块，以更新相关参数[17]；

7)若迭代次数达到最大值Tmax，输出最优方案，否则转至步骤2)。

4 算例分析

4.1 数值设置

本文中优化求解未来24 h的调度策略，取滚动优化中Δt为15 min，M为1 h。电负荷功率、风电出力值参考我国北方某市某楼宇的夏季典型日历史数据，采用智能预测方法对未来24 h内的电负荷及风电出力进行预测，如图4所示。

图4 风电出力和电负荷预测数据

设定风电出力、需求弹性系数和需求恢复初始场景为2 000，将风电出力样本数削减为6，需求弹性系数和需求恢复样本数削减为5，最终得到150个混合场景。以风电出力为例说明典型场景选取过程，如图5所示。其中场景s1—s6为在优化周期开始的1 h内削减后风机可能出力的6个场景。

图5 第一优化周期风电出力样本

将每一天分为峰、平、谷3个时段，表1所示为每天各时段的电价参数。由表可知，实施分时电价后峰时段电价提高25%，谷时段电价降低25%，平时段电价保持不变。

表1 每天各时段的电价参数

4.2 仿真结果

为了研究分时电价与滚动优化对风电消纳的影响，本文中对4种不同案例进行对比，如表2所示。

表2 4种不同案例的对比

表3所示为4种案例最大负荷和最小负荷分布情况。对4种不同案例的优化结果进行对比可以看出，考虑需求响应和滚动优化方法后，需求侧的负荷分布状况改变非常明显。案例1的负荷峰谷比最大，原因是既没有考虑需求响应，也没有加入滚动优化方法。案例2、 3的峰谷比都小于案例1的，这是因为考虑负荷的需求响应后可以转移负荷， 在负荷高峰时段提高电价或天然气价格，负荷低谷时段降低价格鼓励用户进行负荷转移，所以削减了峰谷差，并且滚动优化也对减小峰谷差有积极影响。滚动优化出未来M时间段内的控制序列后只下发第1个时间段内的指令，下一次优化要根据最新预测信息进行重新优化， 使得优化结果更贴近于实际， 减少了风电出力不确定性的影响， 减小了负荷峰谷差。 从表3可以直观地看出， 案例4在平滑负荷需求曲线方面优于其他3种案例， 低谷电价时负荷水平的提高抵消了风电出力反调峰特性对系统优化调度影响。

表3 4种不同案例的负荷峰谷比

表4所示为4种案例的风电上网电量和消纳比例。从表中可以看出，案例4的风电上网电量和消纳比例都高于其他3种案例的，结合表3中4种案例的负荷峰谷差可知，考虑负荷需求响应和滚动优化后，减少了负荷峰谷差，增加了负荷低谷时的负荷需求，系统在谷时段会消纳更多的风电，提高了风电上网电量的比例，降低了因风电的反调峰特性产生的弃风弃电水平。

表4 4种不同案例的风电消纳优化结果

表5所示为4种案例下系统的运行成本。结合表4中的数据可以看出，本文中提出的考虑负荷需求响应并基于滚动优化方法的综合能源系统源-荷联合优化模型能够以最小的运行成本换取系统最高的风电消纳比例。

表5 4种不同案例的系统运行成本

5 结论

本文中针对综合能源系统风电消纳能力不足的问题，将用户侧的需求响应作为主要的消纳方法并与能源侧各设备相协调，提出了源-荷互动综合能源系统优化方法。仿真结果表明：

1)在综合能源系统源-荷配合优化中考虑分时电价需求响应，可以提高柔性负荷削峰填谷能力，使用户负荷曲线更平滑。

2)引入场景树的概念，通过滚动优化求解设备的运行策略减小了风电、负荷的预测误差，减弱了风机出力不确定性对系统的影响。

3)在风电并网问题中考虑需求响应和滚动优化可以明显降低负荷的峰谷差，使得负荷需求与风电出力更匹配，可以消纳更多的可再生能源，减少弃风弃电现象的发生，并且提高了风电的利用效率和高效率燃煤机组的利用水平。