基于遗传算法和非线性规划求解信息交互的光伏阵列模型鲁棒参数辨识方法
郑银燕,胡桂廷,张正江,闫正兵,朱志亮
(温州大学 电气数字化设计技术国家地方联合工程实验室,浙江 温州 325035)
0 引言
太阳能光伏发电由于不受能源资源、原材料和应用环境的限制,具有最广阔的发展前景,是各国最着力发展的可再生能源技术之一[1],其主要优点是能够将太阳能直接转化为电能[2],光伏阵列作为其中的一部分,发挥着越来越重要的作用。
光伏阵列模型在可用性和经济性方面会影响耗电系统的性能[3]。此外,对光伏阵列建模可以推动最大功率点跟踪技术的发展。因此,对光伏阵列建模是十分有必要的。
参数辨识是根据实验数据和建立的模型来确定一组参数值,使得由模型计算得到的数值结果能最好地拟合测试数据,从而可以为生产过程进行预测,提供一定的理论指导[4]。
国内外许多学者都对光伏阵列建模和参数辨识做了相关的研究。师楠[5]等在单二极管电路模型的基础上,提出了光伏电池的Bezier函数建模方法,借助Bezier函数对光伏电池的输出特性曲线进行拟合。李宗鉴[6]等提出了使用有限测量信息构建光伏组件,并用加权最小二乘法进行参数辨识。但当数据存在显著误差时,用该方法进行参数辨识所得的结果会整体上移或整体下移,并不精确。在此基础上,陈倩[7]等提出了基于相关熵的鲁棒参数辨识方法,将非线性规划方法与相关熵的鲁棒参数辨识方法结合,当测量数据仅存在随机误差或存在显著误差时,所得模型输出值与实际光伏阵列的测量值偏差很小。但该方法中的非线性规划容易使所得解陷入局部,不能很容易得到最优解。程泽[8]等利用自适应混沌粒子群算法对光伏电池模型进行参数辨识,增强了算法在全局搜索与局部搜索的平衡性,提高了参数辨识的准确性和可靠性。但该方法存在优化时间长、实现较为复杂等问题。
针对以上方法的优缺点,本文提出了遗传算法与非线性规划结合的鲁棒参数辨识方法。将遗传算法与非线性规划求解信息交互,不仅可以进行全局搜索,还可以进行局部搜索,更易得到问题的全局最优解。同时,使用鲁棒参数辨识方法,使数据在含有显著误差的情况下不受影响,得到较好的结果。通过仿真测试,表明了该方法在光伏阵列模型参数辨识方面具有较高的准确性和可靠性。
1 光伏电池和光伏阵列的数学模型
1.1 光伏电池的数学模型
光伏电池是利用光生伏特效应(Photovoltaic Effect,简称光伏效应)把接收到的光能直接转变为电能的器件。
在实际应用中,为了简化计算,光伏电池在理想情况下的等效电路如图1所示[9]。

图1 光伏电池的等效电路
根据二极管特性及基尔霍夫电流定律可得:
Ipv=Iph-Id=
Iph-I0(eq(Vpv+IpvRs)/(AkT)-1)
(1)
式中,Ipv为光伏电池输出电流(A);Iph为光生电流(A);Id为二极管正向电流(A);I0为二极管反向饱和电流(A);Rs为串联电阻值(Ω);q为单位电荷(1.6×10-19C);Vpv为光伏电池输出电压(V);A为二极管品质因数;k为玻耳兹曼常数(1.3×10-23J/K);T为绝对温度(K)。
当电路短路时,电池在工作温度T,光照强度G下的参数可用以下式子计算[10]:
Iph-ref=Isc-ref
(2)
(3)
(4)
(5)
(6)
(7)
(8)

1.2 光伏阵列的数学模型
光伏阵列是由若干个光伏电池串并联组成的。2×2的光伏阵列简化图如图2所示,其中包含旁路二极管,主要作用是保护光伏电池。
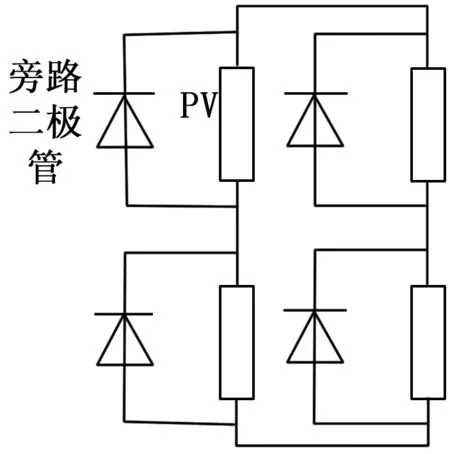
图2 2×2的光伏阵列简化图
根据基尔霍夫定律,在理想情况下,当光伏电池串联个数为Ns、并联个数为Np时,该光伏阵列的输出特性表示如下:
VA=NSVpv
(9)
IA=NPIpv
(10)
PA=NSNPPpv
(11)
其中:VA、IA、PA分别为光伏阵列输出电压、输出电流、输出功率;Vpv、Ipv、Ppv分别为光伏电池的输出电压、输出电流、输出功率。
综上,光伏阵列数学模型可表示为:
IA=NP(Iph-I0(eq(VA/NS+IA/NP*RS)/(AKT(G))-1))
(12)
虽然已经得到光伏电池和光伏阵列的数学模型,但仍存在一些问题:模型参数未知;测量数据有随机误差和显著误差。因此需要分别在随机误差和显著误差情况下,通过参数辨识方法将模型所得结果与实际测量值进行参数辨识,以便得到更精确的模型参数。
2 鲁棒参数辨识问题构成
在实际过程中,由于测量仪器存在一定的误差,光伏电池输出电压和输出电流的测量值与实际值之间会存在偏差,可利用模型信息校正测量值来提高测量的精度。由于太阳能电池板的结板温度T、光照强度G、串联电阻值R和二极管的品质因数A是影响光伏电池建模的主要因素,因此本文主要对该四个参数进行辨识。光伏电池模型参数辨识方法对光伏电池模型参数的确定有非常重要的意义,本文使用的是相关熵鲁棒参数辨识方法。
构造的光伏电池模型参数辨识问题如下:

(13)

(14)

该方法鲁棒性非常强,可以减少随机误差和显著误差对参数辨识的影响,但其也存在一些问题:当遇到较为复杂的问题时,求解会比较困难、计算时间较长;若问题存在多个局部极小点时,可能得到的解并不是实际的最优解。
3 遗传算法与非线性规划求解信息交互优化算法
非线性规划研究一个n元实函数在一组等式或不等式的约束条件下的极值问题[11]。该方法对简单凸函数进行极值求解非常快速方便,但遇到复杂非凸函数时求解比较困难,且易于陷入局部最小值。由于遗传算法的全局搜索能力较强,因此本文采用遗传算法与非线性规划结合的优化算法,全局搜索能力和局部搜索能力都较强,可以得到问题的全局最优解。
遗传算法与非线性规划求解信息交互优化算法流程图如图3所示。该优化算法步骤如下。
步骤1:对种群进行初始化,得到第一代种群,并按式(15)计算其适应度值F。
F=of+λ|ceq|
(15)
其中:of为目标函数,即式(13);λ为常数,本文中取10 000;|ceq|为模型所得值与实际值之差的绝对值。
步骤2:进行选择操作:根据与目标函数相关的一些标准,存活的概率与每个个体相关。
步骤3:进行交叉操作:在交叉过程中,新的个体被创造出来,这些新个体继承了上一代的基因。
步骤4:进行变异操作:每个新个体的基因有变异的可能性。当一个基因发生变异时,与这个基因相关的值也随之改变。
步骤5:判断进化次数是否为N的倍数,本文中N取10。若是,则将遗传算法得到的信息作为初值点,代入非线性规划方法中进行求解,否则跳至步骤6。
步骤6:非线性规划求解信息代入适应度函数中,进行适应度值计算。
步骤7:判断是否满足终止条件,若是,则结束进程;否则跳至步骤2。

图3 遗传算法与非线性规划求解信息交互优化算法流程图
4 仿真及分析
4.1 光伏电池仿真及分析
根据上文内容,建立Rs为0.1 Ω,A为57.485的光伏电池理论数学模型。基于该模型,在T为28℃,G为300 W/m2的条件下产生45组测量电压和测量电流数据。考虑测量数据仅含随机误差和含显著误差两种情况,使用基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法进行参数辨识。
当测量数据仅含随机误差时,所得V-I特性曲线如图4所示。
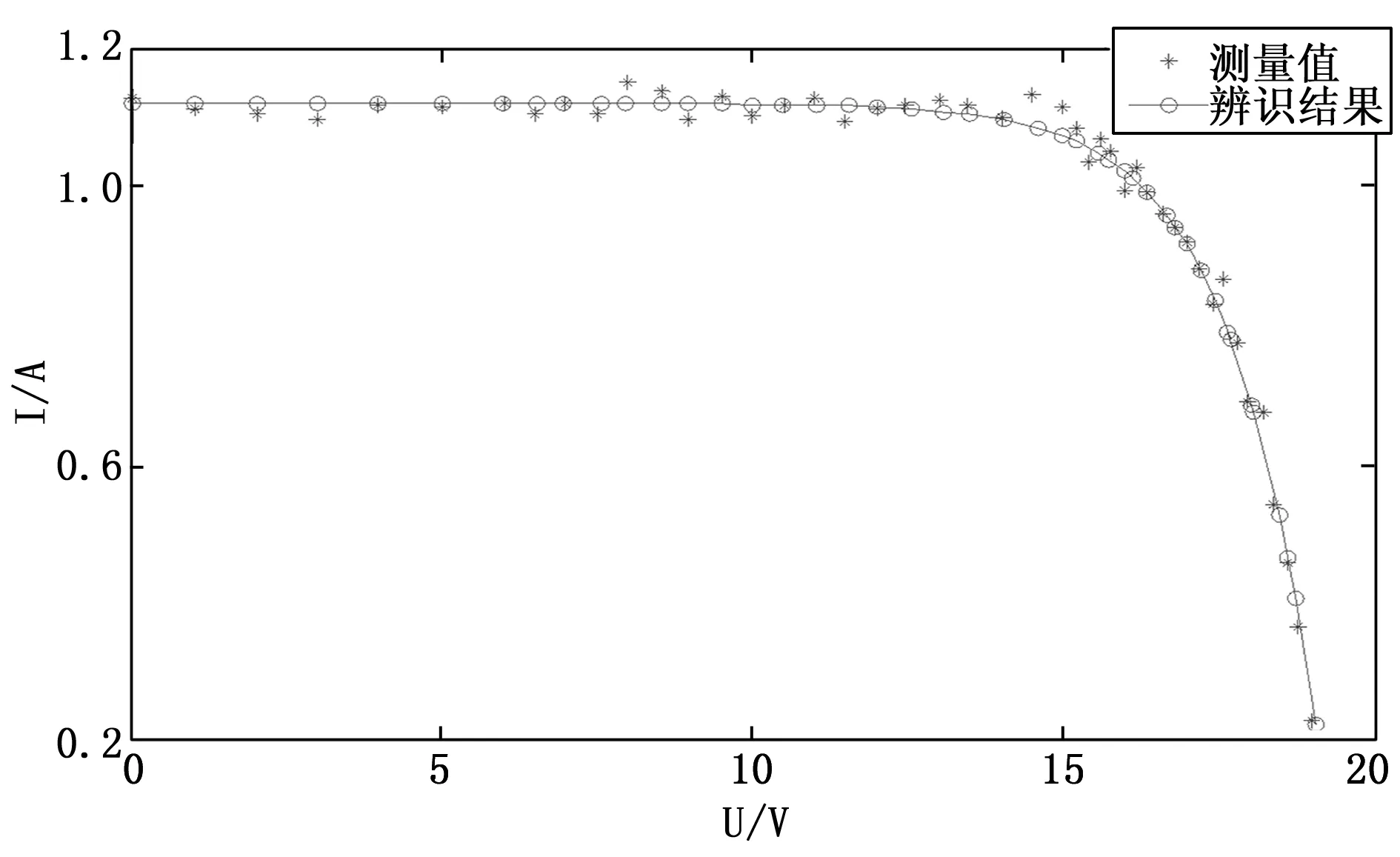
图4 测量数据仅含随机误差时V-I特性曲线
从图4可知,当测量数据仅含随机误差时,使用基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法后所得模型输出值和测量值大体上是重合的。该方法辨识后的光伏电池板的结温为27.995 2℃,光照度为299.317 1 W/m2,Rs和A分别为0.080 4 Ω和55.998 4。
在该情况下分别用非线性规划方法及其结合遗传算法进行求解信息交互对光伏电池进行参数辨识,所得结果如表1所示。

表1 非线性规划方法及其结合遗传算法对光伏电池>进行参数辨识所得结果(仅含随机误差)
从表1可知,当数据仅含随机误差时,基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法所得结果均优于非线性规划所得结果。
在45组测量数据中随机选择3组引入显著误差,显著误差的幅度大小为0.3A,基于遗传算法和非线性规划的参数辨识方法所得结果如图5所示。

图5 测量数据含随机误差和显著误差时V-I特性曲线
从图5中可知,加入显著误差后,使用基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法后所得V-I特性曲线基本与仅含随机误差情况下重合。该方法辨识后的光伏电池板的结温为28.0136℃,光照度为302.137 4 W/m2,Rs和A分别为0.080 1 Ω和53.719 0。
当数据含显著误差的情况下,分别用非线性规划方法及其结合遗传算法进行求解信息交互对光伏电池进行参数辨识,所得结果如表2所示。
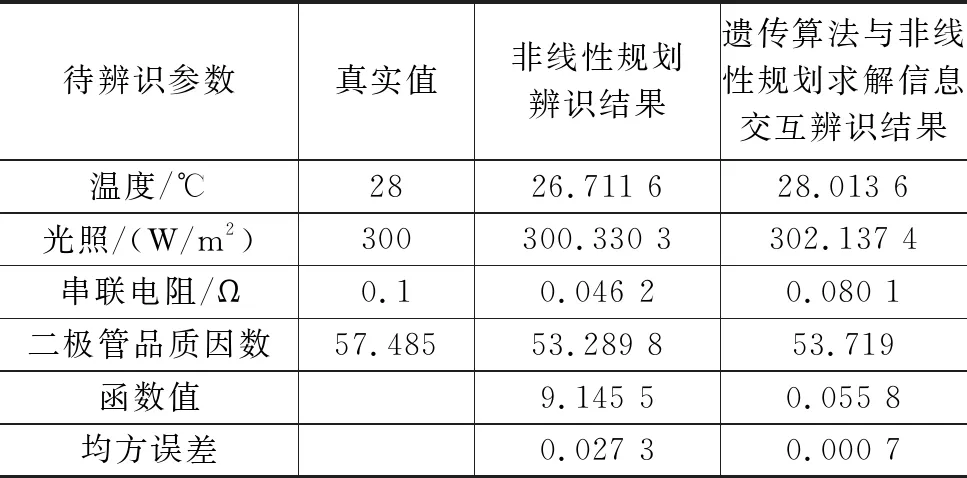
表2 非线性规划方法及其结合遗传算法对光伏电池>进行参数辨识所得结果(含显著误差)
从表2可知,当数据含显著误差时,基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法所得结果除光照之外,也均优于非线性规划所得结果。可以说明基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法有较高的精确度。
4.2 光伏阵列仿真及分析
根据上文内容,建立2×2的光伏阵列理论数学模型,其中Rs为0.1 Ω,A为60.685 4。基于该模型,在T为15℃,G为180 W/m2的条件下产生50组测量电压和测量电流数据。考虑测量数据仅含随机误差和存在显著误差两种情况,使用基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法进行参数辨识。
当测量数据仅含随机误差时,所得V-I特性曲线如图6所示。

图6 测量数据仅含随机误差时V-I特性曲线
从图6可知,当测量数据仅含随机误差时,使用基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法后所得模型输出值和测量值大体上是重合的。该方法辨识后的光伏电池板的结温为14.996 8℃,光照度为178.209 8 W/m2,Rs和A分别为0.102 0 Ω和58.517 2。
当测量数据仅含随机误差的情况下,分别用非线性规划方法及其结合遗传算法进行求解信息交互对光伏阵列进行参数辨识,所得结果如表3所示。
从表3可知,当数据仅含随机误差时,基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法所得结果除光照外均优于非线性规划所得结果。

表3 非线性规划方法及其结合遗传算法对光伏阵列>进行参数辨识所得结果(仅含随机误差)
在50组测量数据中随机选择3组引入显著误差,其幅度大小为0.3 A。基于遗传算法和非线性规划求解信息交互的参数辨识方法所得结果如图7所示。

图7 测量数据含显著误差时V-I特性曲线
从图7中可知,加入显著误差后,使用基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法后所得V-I特性曲线基本与仅含随机误差情况下重合。该方法辨识后的光伏电池板的结温为14.996 4℃,光照度为180.837 6 W/m2,Rs和A分别为0.083 8Ω和58.960 5。
当数据含显著误差的情况下,分别用非线性规划方法及其结合遗传算法进行求解信息交互对光伏阵列进行参数辨识,所得结果如表4所示。

表4 非线性规划方法及其结合遗传算法>对光伏阵列进行参数辨识所得结果(含显著误差)
从表4可知,当数据含有随机误差和显著误差时,基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法所得结果除光照和串联电阻之外,也均优于非线性规划所得结果。基于遗传算法和非线性规划求解信息交互的鲁棒参数辨识方法所得结果中光照和串联电阻与非线性规划所得结果相差不多,且该方法所得误差远小于非线性规划所得结果的误差。
5 结束语
光伏阵列的建模和参数辨识是一个重要的理论课题,国内外都有很多专家学者对此进行了研究并提出了各自的方法,但很多方法仍存在一些问题,比如容易陷入局部、实现较为复杂等。针对这些问题,提出了基于遗传算法和非线性规划求解信息交互的光伏阵列模型鲁棒参数辨识方法,将遗传算法与非线性规划相结合,利用求解信息交互,很好地平衡了全局搜索和局部搜索,同时使用相关熵的鲁棒参数辨识方法,当数据在含有显著误差时也可以得到精度更高的解。最后,通过仿真测试,验证了该方法在参数辨识方面具有较高的准确性和可靠性。

