操作目标利率的选择与传导
童晶 汤春玲
摘 要:依据2014-2018年月度数据,运用VAR模型考量MLF利率与隔夜利率对贷款加权利率、商业银行行为以及金融市场利率与金融市场波动的影响。结果表明:MLF利率对贷款加权利率和商业银行行为的影响较大,隔夜利率对金融市场利率和金融市场波动的影响较大。鉴此,应利用MLF利率调节贷款加权利率与商业银行行为,利用隔夜利率调节金融市场利率与金融市场波动,当两种利率的调节效果收敛接近时,再最终确定唯一的操作目标利率。
关键词: 操作目标利率;MLF利率;隔夜利率
中图分类号:F831.6 文献标识码: A 文章编号:1003-7217(2021)01-0026-07
一、引 言
中国人民银行从2015年开始,试行利率走廊调控机制,将常备借贷便利利率(SLF)作为利率走廊的上限,超额准备金存款利率作为利率走廊的下限。目前,利率走廊初具雏形,但操作目标利率传导的有效性尚有待进一步提高。因此,讨论操作目标利率能够在多大程度上引导贷款利率与金融市场利率,对于拓展发展中国家的利率市场化理论,建立有中国特色的利率走廊,深化利率市场化改革,引导商业银行的行为选择,降低金融体系的整体风险有重大意义。
国外学者对操作目标利率选择与传导研究较多。有学者论证了利率走廊的可行性,比如Binici等(2013)认为利率走廊可以调节信贷利差,有潜力作为一种宏观审慎工具调节经济[1]。Bulut(2015)认为利率走廊可以显著影响信贷和总需求[2]。Aysan等(2015)认为利率走廊显著地降低了跨境资本的敏感性[3]。Kurum和Oktar(2020)认为利率走廊对经济增长、外商直接投资和汇率变量均有影响[4]。随着利率市场化改革的深入推进,越来越多的国内学者开始关注在中国实施利率走廊的可行性,牛慕鸿等(2017)认为我国可以建立一个以常备借贷机制利率为上限、超额存款准备金利率为下限的利率走廊机制[5]。徐忠(2017)研究了危机以来国内外货币政策的变化,认为我国银行体系利率已经具备构建利率走廊的条件[6]。刘澜飚等(2017)认为SLO、SLF、MLF和PSL可以作为利率走廊的上下限[7]。
有学者则研究了利率走廊模式中,操作目标利率引导市场利率的重要性。Fleming等(2010)认为常备借贷便利缩小了利差,能够有效调控市场利率[8]。Christensen等(2014)认为美联储所采取的一系列操作目标利率显著地稳定了短期利率波动[9]。Lee(2016)认为央行可以降低利率的波动性,并且由于存在扭曲,一些看似对称的走廊可能是非对称的[10]。国内学者中,潘敏等(2018)认为借贷便利能够有效地引导市场利率,平抑利率波动[11]。张炎涛和王溪岚(2019)研究了关键政策利率对市场基准利率的引导效应,认为操作目标利率与市场利率之间存在协整关系,能够引导市场利率调整[12]。
有学者检验了操作目标利率传导的有效性。Giannone等(2011)研究了ECB在金融危机时期所采取的政策,认为常备借贷便利这一操作目标利率有效地抑制了衰退[13]。Hrung和Seligman(2015)研究了短期货币市场对国债的影响,认为美联储的SLF显著地影响了回购利率[14]。 AHN和EK(2018)研究了多种政策利率对零售利率的非对称作用,认为土耳其央行平均融资利率和银行间回购利率是非常规利率时期改变零售利率的主要驱动因素[15]。国内学者中,中国人民银行长沙中心支行课题组(2015)研究了我国利率调控体系,认为在利率走廊模式下,央行的操作利率对宏观经济具有有效的预测能力[16]。马理等(2017)研究了在零利率下限背景下的货币政策传导,认为当利率触及零利率下限时经济会出现巨幅波动[17]。徐忠和李宏瑾(2019)研究了隔夜利率作为目标利率的合理性,认为隔夜利率有助于完善利率走廊机制[18]。
由此可见,关于利率走廊的可行性以及操作目标利率的重要性,学者们基本达成了共识,但关于操作目标利率的选择与有效性,目前还并没有相对一致的结论。我国当前正处于从数量型货币政策调整方式向价格型货币政策调整方式转化的过渡时期,在商业银行与金融市场相对割裂的现实环境中,实施单一制的操作目标利率制度可能难以充分有效地达到精准调控的货币政策目标。
二、理论基础与实证模型
(一)理论基础
在货币经济学中,货币政策传导机制是指央行的货币政策,经过信贷、汇率、利率或非货币资产等渠道传导到实体经济,通过影响社会经济活动,进而实现货币政策目标的全过程。其中,利率渠道是市场经济条件下最常规使用的货币政策传导渠道。利率渠道的常规传导机理是,利率降低意味着厂商的生产成本下降,居民的现期消费成本降低,于是厂商支出与消费者支出增加,从而降低失业率并增加就业机会;反之则会降低厂商支出与消费者支出,给经济降温。随着市场经济改革的推进,我国的货币政策正在从传统的以货币供应量为核心的数量型货币政策调整方式,向以利率市场化为核心的价格型货币政策调整方式进行转变。从国际上看,利率走廊是利率市場化的主流模式,央行确定利率走廊的上下限,再通过操作目标利率引导市场利率在利率走廊内部进行波动。如果市场利率超出了利率走廊的上下限,中央银行会调整操作目标利率,引导市场利率回到利率走廊中来。而中国人民银行主要是利用存贷款的基准利率来调节市场利率,这可能会存在一些缺陷:比如与商业银行行为调整和金融市场的实际波动脱节等。在此背景下,货币当局需要寻找到一个有效的操作目标利率来引导市场利率,它是利率市场化的核心指标与关键环节。
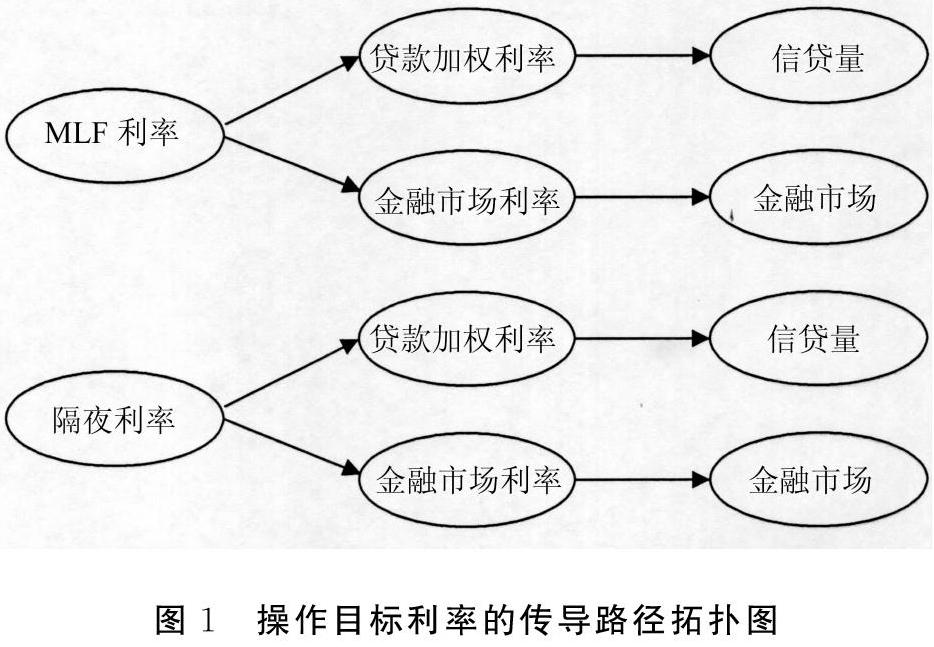
基于以上分析,结合我国金融发展的现状与特点,我们尝试分析可能存在的两组共四条货币政策传导路径。图1为操作目标利率的传导路径拓扑示意图。
(二)模型选择
由于需要检验的变量之间存在着交互影响与滞后影响,而向量自回归(VAR)的统计技术擅于处理变量间的交互与滞后影响,因此,我们使用VAR来检验利率调整的货币政策的传导效果。向量自回归统计模型的标准形式为式(1):
设计两组VAR模型并进行对比检验。第一组包含图1的第一幅子图的两条路径,变量向量集为Yt =(r, wr,C,mr,A)-1;第二组包含图1的第二幅子图的两条路径,变量向量集为Yt =(Shibor, wr,C,mr,A)-1。其中,r为MLF利率,Shibor为隔夜利率,wr为贷款加权利率,C为信贷量,mr为金融市场利率,A为金融市场波动。首先,在第一组VAR模型中,对比检验MLF利率的哪条路径更有效;其次,在第二组VAR模型中,对比检验隔夜利率的哪条路径更有效;再次,将两组VAR模型的结果结合起来,对比检验MLF利率与隔夜利率的传导效果。
由于MLF创设于2014年9月,为了统计检验的统一性,变量数据选取2014年10月至2018年12月的月度数据。其中,MLF利率按中国人民银行每月发放的中期借贷便利金额进行加权得到平均利率,具体做法是用本月不同期限的MLF利率和对应的MLF操作金额的乘积求和,再除以本月总的MLF贷款金额;贷款加权利率来源于人民银行的货币政策执行报告,由于货币政策执行报告只有季度数据,所以,我们使用Eviews的Linear-match last方法将样本空间里的贷款加权利率转变为月频数据;信贷量的数据来源于中国人民银行网站的公开材料;金融市场利率来源于上海银行间同业拆放利率网站的公开材料,将每个月的Shibor的3个月利率的日利率求平均得到该月的Shibor的3个月利率;金融市场波动使用上证指数替代,数据来源于东方财富网,具体见表1。
三、数据处理
(一)平稳性检验
VAR模型需要使用平稳性数据,所以先对各数据序列进行平稳性检验。由于各数据均为时间序列数据,因此使用ADF法检验,检验结果如表2所示。在显著性水平为5%的前提下,变量r、Shibor、C、mr、A为一阶单整序列,变量wr是二阶单整序列。为了保证数据的平稳性以及模型估计的有效性,采用变量的二阶差分序列进行统计检验①。
(二)协整检验
在序列平稳的前提下,协整检验的结果如表3所示。对第一条传导路径“MLF利率—贷款加权利率—信贷量”而言,变量d(r,2)与变量d(wr,2)、变量d(wr,2)与变量d(C,2)存在协整关系;对第二条传导路径“MLF利率—金融市场利率—金融市场”而言,变量d(r,2)与变量d(mr,2)、变量d(mr,2)与变量d(A,2)存在协整关系;对第三条传导路径“隔夜利率—贷款加权利率—信贷量”而言,变量d(Shibor,2)与变量d(wr,2)、变量d(wr,2)与变量d(C,2)具有协整关系;对第四条传导路径“隔夜利率—金融市场利率—金融市场”而言,变量d(Shibor,2)与变量d(mr,2)、变量d(mr,2)与变量d(A,2)存在协整关系。上述结果说明四条操作目标利率的传导路径中的各相邻变量之间均具有长期的均衡关系,因此可以进行后续的量化分析。
(三)确定最优滞后阶数
在建立VAR模型之前,还需要对模型进行最优滞后阶数的判断。结果如表4所示,根据FRE、AIC和HQIC准则,得到第一组变量与第二组变量的最优滞后阶数均为2阶。
四、脉冲响应
(一)MLF作为货币政策操作目标利率的传导路径的脉冲响应
如图2所示,MLF利率增加很快推高了贷款加权利率,在第3期达到正向的峰值,说明MLF利率对贷款加权利率的引导作用快速而有效,如图3所示,贷款加权利率的增加,迅速导致了信贷量的下降,原因是利率上涨增加了企业的融资成本,所以信贷量会下滑,符合经济学预期,随后信贷量出现宽幅震荡最终落在坐标轴下方。图4显示,MLF利率上涨与金融市场利率的上涨成正比,金融市场利率在第2期达到正向的峰值,说明MLF利率对金融市场利率有引导作用;图5显示,金融市场利率的调整与金融市场波动体现出较强的相关性②。
仔细考察MLF利率传导的两条路径的强度:在图2和图3中,MLF利率正向调整一个单位将导致贷款加权利率最多增加0.008848个单位,贷款加权利率正向调整一个单位将导致信贷量最多减少-1011.682个单位,所以MLF利率通过贷款加权利率传导至信贷量的政策强度的最大效果单位为0.008848×(-1011.682)= -8.9514;在图4和图5中,MLF利率正向调整一个单位将导致金融市场利率最多增加0.128413个单位,金融市场利率正向调整一个单位将导致金融市场最多降低31.66179个单位,所以MLF利率通过金融市场利率传导至金融市场的政策强度的最大效果单位为0.128413×(-31.66179)=-4.0658。以上计算结果显示,图2和图3的传导效果(数值为-8.9514)要强于图4和图5的传导效果(数值为-4.0658),据此:得到以下结论:
结论1 现阶段,MLF利率对贷款加权利率与信贷量的影响强于其对金融市场利率与金融市場波动的影响,即MLF利率对商业银行信贷行为的影响更大。
(二)隔夜利率作为货币政策操作目标利率的传导路径的脉冲响应
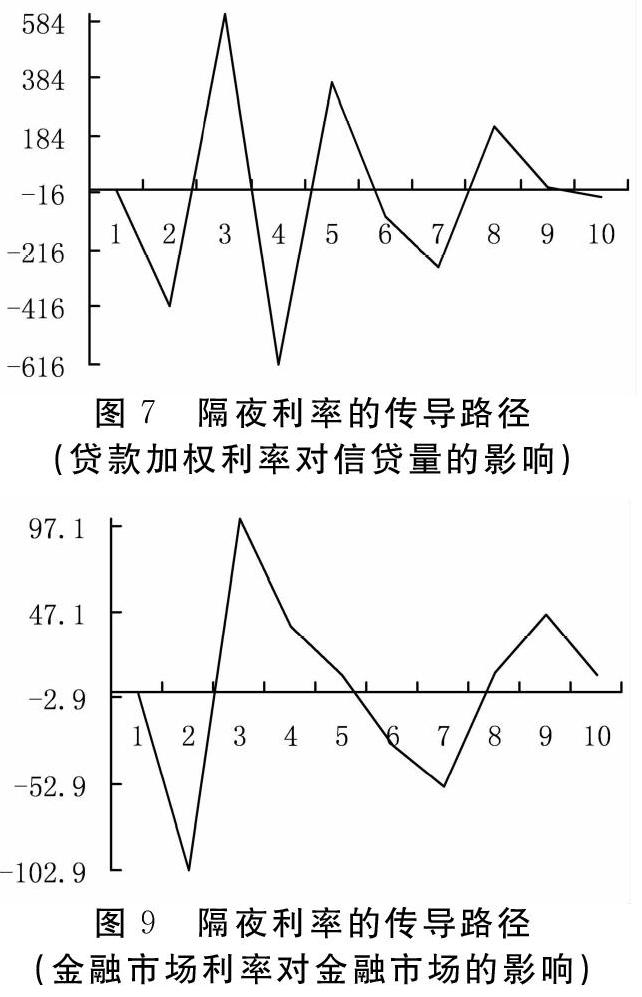
图6显示,隔夜利率增加虽然在初期增加了贷款加权利率,但贷款加权利率随后迅速下降,并在第3期达到负向的峰值,这说明隔夜利率对贷款加权利率的长期引导作用并不理想,隔夜利率与贷款加权利率没有出现预期的同向调整;图7显示,贷款加权利率的增加,导致了信贷量的宽幅波动,但在隔夜利率调整的背景下信贷量波动特征不明显。图8显示,隔夜利率上涨在初期导致了金融市场利率的上涨,经过两期的下跌之后,金融市场利率重新回到正方向并大幅上涨;图9显示,金融市场利率的调整与金融市场波动也体现出较强的相关性。
仔细考察隔夜利率传导的两条路径的强度:在图6和图7中,隔夜利率正向调整一个单位将导致贷款加权利率最多增加0.010295个单位,贷款加权利率正向调整一个单位将导致信贷量最多减少-616個单位,所以隔夜利率通过贷款加权利率传导至信贷量的政策强度的最大效果单位为0.010295×(-616)= -6.34172;在图8和图9中,隔夜利率正向调整一个单位将导致金融市场利率最多增加0.090954个单位,金融市场利率正向调整1个单位将导致金融市场最多降低-102.8965个单位,所以隔夜利率通过金融市场利率传导至金融市场的政策强度的最大效果单位为0.090954×(-102.8965)=-9.3588。计算结果显示,图8和图9的传导效果(数值为-9.3588)要强于图6和图7(数值为-6.34172)的传导效果,据此得到:
结论2 现阶段,隔夜利率对金融市场利率与金融市场波动的影响强于对贷款加权利率与信贷量的影响,即隔夜利率对金融市场波动的影响更大。
再将图2、图3与图6、图7的数据进行比较:“MLF利率-贷款加权利率-信贷量”的货币政策传导强度为-8.9514,“隔夜利率-贷款加权利率-信贷量”的货币政策传导强度为-6.34172,前者大于后者,再次证明了结论1,说明当前对商业银行行为的影响更多来源于MLF利率调整。然后,把图4、图5与图8、图9的数据放在一起比较:“MLF利率-金融市场利率-金融市场波动”的货币政策传导强度为-4.0658,而“隔夜利率-金融市场利率-金融市场波动”的货币政策传导强度为-9.3588,后者要大于前者,再次证明了结论2,说明当前对金融市场波动的影响主要来源于隔夜利率的调整。
但是,数据同时也显示,MLF利率传导到贷款加权利率、MLF利率传导到金融市场利率、隔夜利率传导到贷款加权利率,以及隔夜利率传导到金融市场利率的效率并不太高,数值分别只有0.008848、0.010295、0.128413,以及0.090954个单位,计算的结果意味着:
结论3 我国现阶段利率传导的效果尚不十分突出,还需要进一步深入推进利率市场化改革。
五、方差分解
方差分解的主要作用是分析一个变量对另外一个变量的解释力度,因此,可以通过方差分解的数据,研究MLF利率与隔夜利率能在多大程度上解释其他经济变量的变化,同时也可检验与对比MLF利率与隔夜利率的传导有效性,判断不同的操作目标利率传导的主要途径。
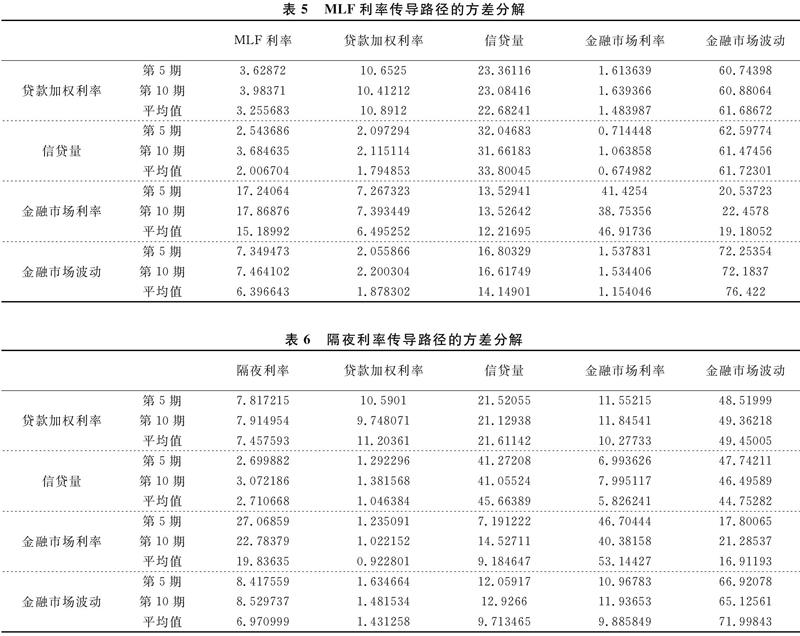
表5与表6是MLF利率与隔夜利率的传导路径的方差分解结果。由于在图1的拓扑示意图中,给出了MLF利率与隔夜利率可能存在的四条传导路径,所以下面结合表5与表6方差分解的结果对这四条传导路径进行对比分析。
第一条传导路径“MLF利率→贷款加权利率→信贷量”:从MLF利率至贷款加权利率传导的解释力度为3.26/(100-95.26),从贷款加权利率至信贷量传导的解释力度为1.79/(100-33.80),两者相乘得到该传导的全路径的解释力度为0.0186③。
第二条传导路径“MLF利率→金融市场利率→金融市场波动”:从MLF利率至金融市场利率传导的解释力度为15.19/(100- 78.31),从金融市场利率至金融市场波动传导的解释力度为1.15/(100-76.42),两者相乘得到该传导的全路径的解释力度为0.034。
第三条传导路径“隔夜利率→贷款加权利率→信贷量”:从隔夜利率至贷款加权利率传导的解释力度为7.46/(100-82.27),从贷款加权利率至信贷量传导的解释力度为1.05/(100-45.66),两者相乘得到该路径的全路径的解释力度为0.0097。
第四条传导路径“隔夜利率→金融市场利率→金融市场波动”:从隔夜利率至金融市场利率传导的解释力度为19.84/(100- 79.24),从金融市场利率至金融市场波动的解释力度为9.89/(100-72.00),两者相乘得到该路径的全路径的解释力度为0.338。
数据分析的结果显示,由于第一条传导路径的效果(0.0186)要强于第三条传导路径的效果(0.0097),说明当前影响贷款加权利率与信贷量的主要是MLF利率,而不是隔夜利率,再次证明了结论1,即MLF利率对信贷量的影响要强于隔夜利率对信贷量的影响。由于第四条传导路径的效果(0.338)要大于第二条传导路径的效果(0.034),说明当前影响金融市场的主要是隔夜利率,而不是MLF利率,再次证明了结论2,即隔夜利率对金融市场的影响要强于MLF利率对金融市场的影响。同时,由于四条传导路径的数据结果都偏小,所以也再次证明了结论3,即现阶段的利率传导效果尚有待加强,我国还需要进一步深化推进利率的市场化改革。
六、结论与启示
以上研究表明:(1)MLF利率对信贷量的影响要强于隔夜利率对信贷量的影响,若用MLF利率做操作目标利率来调节商业银行行为,会比用隔夜利率做操作目标利率调节商业银行行为更加有效。(2)隔夜利率对金融市场的影响要强于MLF利率对金融市场的影响,若以隔夜利率作为操作目标利率来调节金融市场波动,会比以MLF利率作为操作目标利率来调节金融市场波动更加有效。(3)虽然MLF利率能更加有效地调节信贷量,隔夜利率能更有效地调节金融市场,但无论以MLF利率还是隔夜利率作为操作目标利率,它们的调节效果都偏弱,这一定程度上说明中国利率传导途径尚不十分完善,利率市场化改革还有待进一步加强与深化。
由此得到以下启示:第一,现阶段实施单一制的操作目标利率难以充分达到央行的利率传导的政策意图,在推进利率市场化的进程中,可能需要双操作目标利率的中间过渡阶段。第二,建议同时设置两个操作目标利率,利用MLF利率调节贷款加权利率与商业银行行为,利用隔夜利率调节金融市场利率与金融市场波动。第三,建议当MLF利率和隔夜利率这两种利率的调节效果收敛接近时,再最终确定唯一的操作目标利率。
注释:
① 在使用VAR统计技术进行实证检验之前,应当检验数据序列是否平稳。如果数据序列非平稳,则通过差分转化成平稳序列,进行后续的VAR检验。已有研究证明,对所有变量进行差分后得到的模型與原模型一致,不会影响核心解释变量的估计系数。
② 数据序列主要是原始数据,脉冲图中的信贷量与金融市场的振幅对应着利率冲击下的相关变量的波动幅度,不再对数据进行统一量纲的处理,可以尽最大可能保持数据的原始真实性。
③ 具体的计算过程:以第一条传导路径“MLF利率—贷款加权利率—信贷量”为例,这是一个三层级的传导过程,第一层级变量是MLF利率,第二层级变量是贷款加权利率,第三层级是信贷量。结合货币经济学的理论,影响第二层级变量贷款加权利率的主要是上级变量与同级变量,所以计算时首先要除去自回归影响和其他变量的影响得到分母基数,具体为100-10.8912-22.68241-61.68672=100-95.26,然后再拿上级变量MLF利率的影响除以该影响得到3.26/(100-95.26)。信贷量是第三层级变量,第一层级、第二层级变量以及第三层级的同级变量对它都会有影响,所以计算时首先除去自回归影响,得到分母基数100-33.80,然后再拿上级变量贷款加权利率的影响除以该影响得到1.79/(100-33.80)。综合两步计算,第一条传导路径的全路径的解释力度为两者相乘的结果0.0186。其余的几条传导路径的全路径的解释力度可以依次类推,为节省篇幅不再赘述。
参考文献:
[1] Binici M, Erol H, Hakan A K, et al. Interest rate corridor: A new macroprudential tool?[J].CBT Research Notes in Economics,2013,7(20):1-16.
[2] Bulut U. The interest rate corridors as a macroprudential tool to mitigate rapid growth in credits: Evidence from turkey[J].Theoretical and Applied Economics, 2015, 605(4):133-144.
[3] Aysan A F, Fendolu S, Kilin M. Macroprudential policies as buffer against volatile cross-border capital flows[J]. The Singapore Economic Review, 2015,60(1), 1550001(1-26).
[4] Kurum E , Oktar S . The role of central bank in competitive environment :A study for interest rate corridor systems[M].Hasan D, Serhat Y.Handbook of research on decision-making techniques in financial marketing.Pennsylvania: IGI Global,2020:383-411.
[5] 牛慕鸿,张黎娜,张翔.利率走廊、利率稳定性和调控成本[J].金融研究,2017(7):16-28.
[6] 徐忠.中国稳健货币政策的实践经验与货币政策理论的国际前沿[J].金融研究,2017(1):1-21.
[7] 刘澜飚, 尹海晨, 张靖佳. 欧元区非传统货币政策的发展及对中国的启示[J]. 国际金融研究, 2017,359(3):35-44.
[8] Fleming M J, Hrung W B, Keane F M. Repo market effects of the term securities lending facility[J].American Economic Review, 2010, 100(2):591-596.
[9] Christensen J H E , Lopez J A , Rudebusch G D . Do central bank liquidity facilities affect interbank lending rates?[J]. Journal of Business & Economic Stats, 2014, 32(1):136-151.
[10]Lee J. Corridor system and interest rates: Volatility and asymmetry[J]. Journal of Money Credit & Banking, 2016, 48(8):1815-1838.
[11]潘敏,周闯,刘姗.预调微调、货币市场利率波动与利率走廊机制[J].国际金融研究,2018(12):21-30.
[12]张炎涛,王溪岚.利率市场化改革与关键政策利率的选择——基于国际经验及两区制阈值误差修正模型的分析[J].金融监管研究,2019(2):16-28.
[13]Giannone D, Lenza M, Pill H, et al. Non-standard monetary policy measures and monetary developmentst[M]. Cambridge: Cambridge University Press, 2011: 195-221.
[14]Hrung W B,Seligman J S. Responses to the financial crisis, treasury debt, and the impact on short-term money markets[J]. International Journal of Central Banking, 2015, 11(1): 151-190.
[15]AHN S, EK S. Interest rate pass-through in turkey during the period of unconventional interest rate corridor[J].Quantitative Finance and Economics, 2018, 2(4): 837-859.
[16]中国人民银行长沙中心支行课题组,肖杰.利率市场化背景下我国利率调控体系构建研究[J].金融监管研究,2015(2):10-32.
[17]马理,娄田田. 基于零利率下限的宏观政策传导研究[J].经济研究,2017(11):94-105.
[18]徐忠,李宏瑾.货币价格调控模式下政策目标利率的期限选择[J].国际金融研究,2019(3):3-12.
(责任编辑:钟 瑶)

