下游障碍物位置对溃坝洪水流动特性的影响分析

林晓惠，付成华，王兴华，白 帅，罗天玺

(西华大学能源与动力工程学院，四川 成都 610039)

0 引 言

受水文、地质、施工等不确定因素以及暴雨、洪水、地震等自然灾害的影响，溃坝事故时有发生，溃坝带来的损失也是非常惨痛的。随着计算机技术的发展，数值模拟越来越多地应用到溃坝问题的研究中。王晓玲等[1]针对溃坝洪水在复杂淹没区域的演进，建立了耦合VOF法的三维k-ε湍流数学模型；Marrone等[2]采用delta-SPH模型分析溃坝水流冲击不同形状障碍物时的冲击压力，结果有较高的精度；Biscarini等[3]比较了浅水流动和三维模拟在不同溃坝条件下的计算结果。由国内外研究现状可知，三维数学模型能更精细地模拟自由水面变化强烈的溃坝水流运动过程[4]，是现阶段研究溃坝洪水泛滥区域、洪水深度、流速、洪水波传播时间的热门方法。

由于气候变化，洪水泛滥区频繁引起潜在伤亡和破坏，水流与障碍物间的相互作用导致灾害等级增加，尽管存在这种相关性，但是文献相对较少。本文利用FLUENT软件建立溃坝洪水三维数值计算模型，耦合VOF法和RNGk-ε模型求解RANS方程，并采用PISO算法求解数值计算，模拟溃坝洪水在演进过程中的流动特性，进而研究障碍物位置变化对溃坝洪水流动特性的影响。

1 数学模型及计算方法

1.1 数学模型

1981年，Hirt和Nichols[5]提出了完整的VOF法理论体系和实现方法，广泛应用于多种不混溶流体流动过程的截面捕获。通过求解流体相体积分数方程，完成对各相之间界面的追踪，从而实现对自由表面的追踪[6]。方程如下

(1)

式中，相体积分数F=F(x，y，z，t)，定义为离散网格中各相流体的体积与网格体积的比值，且F∈[0，1]。

RNGk-ε湍流模型是由Yakhot等[7]使用重新归一化组(RNG)方法开发的。

湍流动能k输运方程

(2)

耗散率ε输运方程

(3)

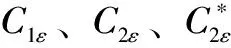
1.2 计算方法

基于有限体积法离散控制方程，包括连续方程、运动方程和能量方程[8]。对于黏性不可压缩均质流体，ρ、μ、k均视为常数，于是控制方程组为

连续方程

水利现代化绘河清湖晏蓝图——访江苏省淮安市水利局局长、党委书记黄克清……………………………… 韦凤年，江 芳，郭 纯等(16.59)

∇u=0

(4)

N-S方程

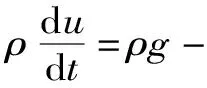
(5)

能量方程

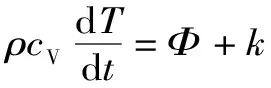
(6)

式中，ρ为密度；t为时间；u为流速；g为重力加速度；p为压力；μ为流体黏度；cV为比定容热容；T为热量；Φ为耗散函数；k为热传导系数；q为辐射或其他原因单位时间传给单位质量流体的热量。

对于离散后的代数方程，选用FLUENT压力速度耦合算法中收敛性较好的PISO算法进行求解。PISO算法适合瞬态不可压缩流体，是典型的两步校正算法[9]，主要实施步骤包括预估步、第一校正步、第二校正步。

(1)预估。假设压力场p*，利用p*求解动量离散方程，得出速度场u*、v*。

(2)校正1。修正p*，求解压力修正方程得到p′，计算压力修正量、速度修正量为u′、v′，得到压力修正值和速度修正值p**、u**、v**。

(3)校正2。对压力修正方程进行修正得到p″，计算压力修正量、速度修正量为u″、v″，得到压力修正值和速度修正值p***、u***、v***。设p=p***，u=u***，v=v***，若修正后压力场对应的速度场能满足连续性方程，则p、u、v为正确的压力速度分量，否则令p*=p，u*=u，v*=v，继续迭代。

2 数值模拟模型及计算条件

2.1 数值模拟模型建立

基于文献[10]的试验模型，在水库下游距闸门1.167 m处布设一45°弧形障碍物，距离左右岸均为0.295 m，初始水位H=0.55 m，简化模型如图1a所示。利用UG建立模型、ICEM划分网格，导入FLUENT进行求解。采用结构化网格，最大网格0.005 m，最小网格0.001 m，网格总数为122 021个。

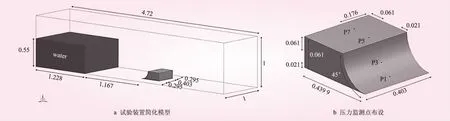
图1 计算模型及测点布设(单位：m)

2.2 边界条件

(1)进口边界条件。重点关注水体自由跌落对障碍物的冲击作用，故进口设置为墙(Wall)，以防止水流从进口处流出。

(2)出口边界条件。在模型顶面和模型出口处设置为压力出口边界条件，参考压力为一个标准大气压值，其中出口处压力值与水深有对应关系，压力值采用用户自定义函数UDF给出。

(3)固壁边界条件。障碍物及模型底部设置为固壁边界(Wall)，采用无滑移边界。糙率取值为0.012。

2.3 模型验证

图2为4个压力测点处的压力模拟值与试验值的对比。从图2可以看出，模拟的压力值随时间变化曲线与试验值吻合程度较好，压力分布能够完全描述实验并且充分模拟压力峰值，可以使用该模型计算分析障碍物位置对溃坝洪水流动特性的影响。

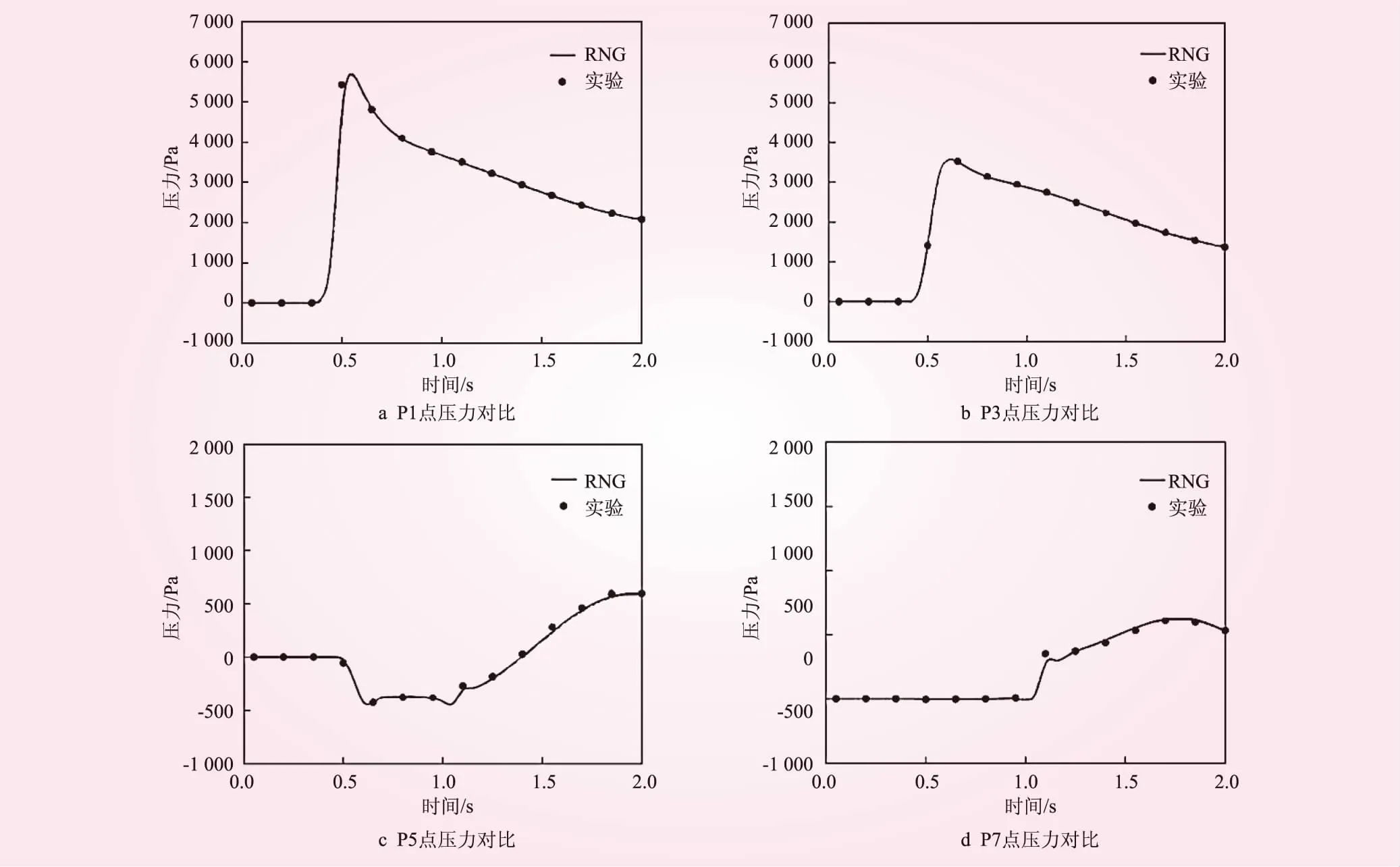
图2 各测点处的压力模拟值与试验值对比

2.4 计算工况

障碍物为45°弧形障碍物，初始水位为H=0.55 m，设置3种工况进行对比分析，即分别设置闸门与障碍物之间的距离L为0.583 5、1.167 m和1.750 5 m。

3 模拟计算结果及分析

3.1 压力分析

对3种工况下的泄洪情况进行模拟，得出各监测点压力随时间的变化，如图3所示，各监测点最大压力对比见表1。由图3、表1可以看出：3种工况下P1点最大压力对比情况为工况3<工况2<工况1，到达时间为工况1<工况2<工况3；P3点压力随时间变化趋势与P1点大致相同；P5点由于挑流作用出现负压；P7点压力值变化不明显。此外，工况3下各监测点处的压力比工况1减少14%～42%，比工况2减少4%～28%。计算各个工况下洪水流过障碍物前后的压力对比情况为：工况1压力减小74%，工况2压力减小73%，工况3压力减小84%。

表1 监测点压力最值对比

图3 不同监测点压力随时间的变化

下游障碍物位置距离溃坝闸门越远，障碍物上各监测点的压力峰值、均值越小，前后变化值相对越大。障碍物各监测点所受压力负值的峰值与距离没有明显的对应关系；障碍物各监测点压力最大值出现时间与距离成正比，即距离越远，压力峰值出现时间越晚。

3.2 水面线分析

3种工况下水面线随时间的变化如图4及表2所示。本次分析将溃坝洪水演进过程分为水流刚到达障碍物底端阶段、水流到达障碍物顶面阶段、水流完全越过障碍物阶段、障碍物下游两端包围的无水区域被淹没阶段、水流到达出口阶段5个阶段。

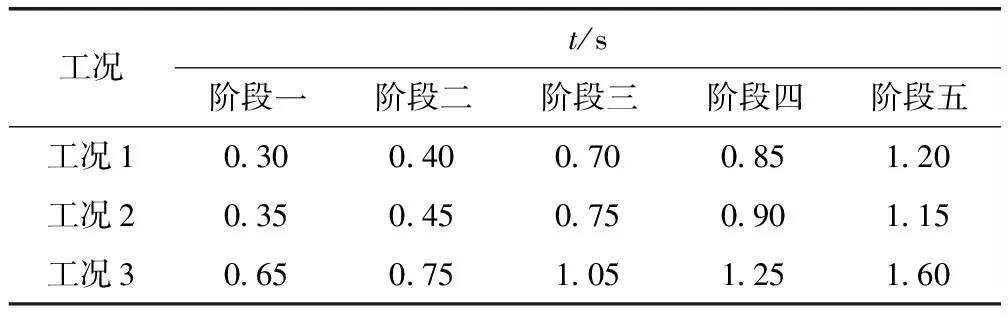
表2 不同工况下水流到达各阶段的时间对比

图4 水面线随时间的变化

从图4及表2可以看出，工况3的挑流时长比工况1增加0.35 s，比工况2增加0.3 s。随着间距的增加，水流到达障碍物各监测点的时间逐渐延后，当间距增大到一定程度时，第四阶段与第五阶段重合，并且间距越大，水流的挑流作用越明显，通过障碍物时向前跃升高度越高。

3.3 流速分析

溃坝洪水向下游演进的过程中，遇到障碍物干扰，由于弧形障碍物对水流有跃升作用，导致水流越过障碍物后水流能量减少，速度明显降低，之后再流向出口。计算3种工况下障碍物前、障碍物后以及出口平均流速变化的对比，见表3。

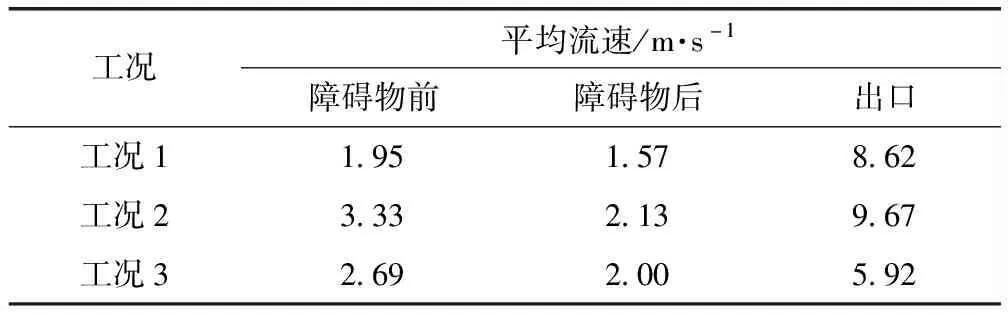
表3 平均流速变化对比

对比3种工况下障碍物前后平均速度的变化情况：工况1减小19.3%，工况2减小36%，工况3减小23.7%。考虑到L的不同，故对比3种工况下洪水出口处平均速度的关系，即工况2的平均速度比工况1增加12.2%，工况3的平均速度比工况1减小33.7%。因此，下游障碍物对水流流速有较大影响，且远端障碍物更能有效地减缓水流流速，消能作用更强。

3.4 影响分析

下游障碍物对溃坝洪水的影响较大，溃坝洪水下泄越过障碍物时会发生挑流现象，且这个挑流的时间、距离随着障碍物与闸门的间距发生变化。在洪水泛滥区，不同位置的障碍物，对溃坝洪水演进过程的影响不同，消能阻水的效果也不同。从模拟结果可见，离闸门远端的障碍物对洪水冲击力的减缓作用大于近端的障碍物。对于实际应用来说，下游障碍物削减的水能远大于模型数据。因此，为达到良好的消峰消能目的，应当考虑下游障碍物的合适位置。

4 结 语

在已有试验模型基础上，本文利用溃坝洪水三维数学模型，模拟计算下游设置45°弧形障碍物的3种工况，得到了溃坝洪水在演进过程中的流动特性，以及障碍物位置变化对溃坝洪水流动特性的影响，对下游消能减灾和防洪设计具有一定的参考意义。后续将结合溃坝方式、溃口变化、地形地貌影响、障碍物形状大小变化等进一步研究溃坝洪水演进特性。