考虑租箱返还限制的集装箱船舶调度优化①

张天宇 杨 硕 郑红星

(大连海事大学交通运输工程学院 大连116026)

0 引言

随着航运市场的竞争加剧,提高竞争力越来越引起航运企业的重视,而日常的船舶调度是提高该类企业竞争力的有效手段之一;就经营班轮航线的航运企业而言,考虑到期租箱返还的船舶调度优化,不仅可以降低企业运营成本,还可部分缓解企业辐射网络中的缺箱和舱位过剩等问题,船舶调度已经引起了越来越多企业的重点关注。

针对船舶调度的相关问题,国内外学者进行了大量的研究,根据研究的侧重点不同,可以分为考虑时间窗的船舶调度问题、空箱调运的船舶调度问题和租箱策略的船舶调度问题三方面。

在考虑时间窗的船舶调度方面,文献[1]研究了时间窗、航速影响的船舶调度问题,建立了船舶成本、总服务成本最小和总利润最大的多阶段模型,并利用仿真进行求解。文献[2]研究了受恶劣天气影响的船舶调度问题,以总成本最小为目标函数建立模型,并设计了嵌入基因修复算子的改进遗传算法进行求解。文献[3]研究了基于船期表、航速及受泊时间窗的船舶调度问题,以总成本最小为目标函数建立非线性数学模型,并用嵌入基因修复的改进遗传算法进行求解。

在空箱调运方面,文献[4]研究了新的空箱调运策略,即不确定目的港策略,以总调运费最小为目标函数建立非线性规划模型,并用Matlab 遗传算法工具箱求解。文献[5]研究了空箱调运路径和空箱重派的联合优化,以成本最低为目标函数构建网络流模型并求解。文献[6]研究了将空箱抽象成资源的空箱调运问题,以费用最低为目标函数构建混合整数模型,并用基于免疫的进化算法进行求解。文献[7]研究了基于动态规划的空箱分配问题,以两港口两航线调运系统建立动态随机模型,并利用模拟仿真验证其有效性。文献[8]研究了结合库存策略的空箱调运问题,以成本最低为目标,基于罚函数建立库存模型,并用启发式算法进行求解。

在租箱策略方面,文献[9]研究了可折叠空箱的适用范围的租箱问题,以成本流最小为目标函数建立网络流模型,用网络单纯形法计算。文献[10]研究了考虑弃货成本及租箱成本的空箱调运问题,以运输系统总收益最大为目标函数建立数学模型,并设计了遗传算法与动态规划的组合算法进行求解。文献[11]研究了基于不同角度的租箱策略问题,建立数学优化模型,并运用数字仿真技术揭示策略运用中的潜在规律。文献[12]研究了新港口的租箱空箱分配问题,以总成本最低为目标函数建立数学模型,并利用Matlab 结合模型特点进行求解。

综上所述,针对考虑时间窗的船舶调度问题的研究,大多以总成本最低为目标,罕有考虑利用船舶调度提高收益而覆盖新增成本的问题;在空箱调运问题的研究中,大多文献以收益最高为目标进行空重舱位分配,但无法在短周期之内改善航运企业空箱分布不均匀的状况;在租箱策略方面,上述文献以租箱成本最低为目标,进行租箱策略选择,但鲜有考虑租箱返还问题的文献。租箱返还问题涉及到时间窗、租箱策略、空箱调运等问题。因此,本文重点考虑租箱的还箱成本控制问题,兼顾空箱调运过程中的船舶调度问题及待还租箱所搭载的船舶方案设计。本文与已有文献不同之处主要有以下两点。

(1)考虑了待还租箱放弃直接归还,选择再次被利用,利用与否取决于收益与所产生的超期费之差。

(2)设计了考虑待还租箱再次被利用的船舶实际航行线路的船舶调度方案。

1 问题描述

随着航运企业的快速发展,租箱策略愈发被广泛应用。在所租空箱的还箱过程中,会造成舱位资源和高利润航线资源的浪费,因此宏观调度各集装箱船舶以及各个待还租箱的运输方案可成为减少此类成本的重要手段,即再次利用待还租箱资源,将空转重,创造更多利润以减少还箱成本。

本文中,班轮公司的辐射点已知,租箱公司所要求的还箱点固定。首先,班轮公司可根据船舶舱位数量及各港口需要运输的集装箱数量自由选择航线;其次,依据待还租箱的还箱路径及到期时间判断租箱是否可以再次被利用;最后,待还租箱可视不同港口的缺箱情况搭载不同的船舶到达缺箱点,由空转重或者由重转空。

本文的问题可描述为:针对某个航运企业的航线辐射网络,在一个运营周期内(从第一条船舶出发时刻开始计时,截止到整个航线网络中最后一条船舶达到目的港的时刻为一个运营周期),已知各船舶进出港时间、港口之间距离、重箱运输量及运费、空箱运输量及运费、待还租箱还箱期限、超期费收费标准、还箱点等相关信息后,以单个周期所有船舶的运输成本最小为目标,建立协同优化模型,研究考虑待还租箱再次被利用的条件下的租箱返还问题,最终给出各条船舶所选航线以及各个待还租箱所搭载的船舶计划方案。航线网络图如图1 所示。

图1 航线网络图

2 数学模型

2.1 基本假设

为切合航运企业运营的实际情况,本文做出如下假设。

(1)所有船舶均可航行于航运企业辐射的各类航线;在航运企业的实际运营过程中,为应对实际的需求变动或各种突发状况一般仅定线不定船,航运企业实际营运的船舶需在该公司辐射的各类航线间跨航线调度。

(2)假设船舶到港等待时间和船舶装卸作业时间已知;在船舶抵港之前,大多数会将该船的预计抵达时间段并连同实际配载信息发送给港口,且港口一般都已提前制定了船舶排队规则和泊位作业计划。

(3)假设待还租箱超期返还只会产生超期费,无其他费用;在待还租箱返还过程中,可能还会产生折旧、清洗等费用,但相对超期费来说,这些费用较低,可忽略。

(4)假设在一个航运周期运营过程中,不考虑再次租赁集装箱;一般来说,航运企业的租箱计划和还箱计划分开,租箱业务属于箱管部门,还箱业务属于航线部分。

2.2 符号说明

(1)集合

N:船舶集合,n=(1,2,…,N)∈N;M:集装箱集合,m=(1,2,…,M)∈M;P:挂靠港集合,i,j=(1,2,…,I,J)∈P;T:目的港集合,k=(1,2,…,K)∈T。

(2)参数

Ri:i港所需归还的集装箱箱量,Ri＞0;Li:i港的缺箱量,Li＞0;Cij:表示从i港到j港的货运量,Cij＞0;Sn:船舶n的容量,Sn＞0;tij:从i港到j港的航行时间,tij＞0;Di:i港的待还租箱的还箱期限,Di为整数;hin:第n条船到i港的载货量(包含空箱),hin＞0;ri:i港的重箱量,Ri:i港的还箱数量,Ri＞0;tin:第n条船航行至i港的时间,tin＞0;din:第n条船所装i港的租箱的超期天数,din＞0;tin:第n条船航行至i港的时间,tin＞0;Cm:第m个箱子的运输成本,Cm＞0;RDm:第m个箱子的产生的超期费,RDm≥0;CRm:第m个重箱产生的收益,CRm＞0;CLi:船舶在i港的装卸成本,CLi＞0;CSm:第m个箱子在停泊时产生的平均成本,CSm＞0;CSijn:第n条船从i港到j港的运输成本,CSijn＞0。

(3)决策变量

xijn:表示第n条船从i港到j港的载货量;fijn:表示第n条船在i港装上来自j港的集装箱箱量,i可以等于j;sijn:表示第n条船在i港卸下来自j港的集装箱箱量;yijn:为0 -1 变量,表示船舶的航行路线信息,若第n条船从i港驶向j港,yijn=1,否则yijn=0。

2.3 模型构建

集装箱调运过程中,为使成本最低,基于整体航线网络,各集装箱船舶根据船舶特点选择不同航线、不同挂靠港口,因而会产生互不相同的各项成本,其中ΣmΣnΣijCm +ΣmΣijRDm -ΣmΣijCRm表示因待还租箱的由空转重或者由重转空所产生的超期费与新增利润之差;ΣmΣnΣijCm × fijn表示集装箱运输成本;ΣnΣijCSijn × yijn表 示 集装箱船舶 的 航行成 本;ΣmΣnΣijCSm × yijn表示船舶停泊所产生的成本;ΣmΣnΣijCLi ×(fijn+sijn) 表示船舶在港的装卸成本。

本文以整体航线网络中所有集装箱船舶运输过程中还箱成本最小为目标,因航线需重新整合,故集装箱船舶运输及作业所产生的成本计入目标函数中,从第一条船舶在始发港作业开始计费,至最后一条船舶在目的港停止作业为止。式(2)表示集装箱船舶所装卸的集装箱数量不得多于个港口的集装箱总数,即维护集装箱船舶的装卸平衡;式(3)表示在各个港口中,待还租箱的总数保持平衡;式(4)表示在一次运输周期内,满足所有待运输的重箱及空箱的总量均可在本次运输活动中全部运输;式(5)表示所有集装箱船舶的舱位数量应容纳待运输集装箱的总数;式(6)表示各港口的缺货情况应保证集装箱船舶驶来或驶去的必要性;式(7)表示待还租箱是否有必要承担超期费而选择再次利用的约束;式(8)表示超期费的计费规则;式(9)～式(10)表示整个活动过程运行的逻辑约束;式(11)～式(12)表示船舶路径选择约束,若xijn＞0 说明船舶n从i港到过j港;式(13)表示待还租箱的路径选择约束,若fipn＞0 说明船舶n从i港装过来自p港的集装箱;若sipn＞0 说明船舶n从i港卸下来自p港的集装箱;式(14)～式(15)表示待还租箱在各个港口装卸数量限制的约束,即m船在i港装的p港集装箱数量要小于其他船舶在i港卸下的p港的集装箱数量,m船在i港装的j港集装箱数量要小于其他船舶在i港卸下的j港的集装箱数量与还箱量的和。

3 算法设计

由于本文重点考虑了待还租箱再次利用的影响因素,因此,目标函数中新增了利润与超期费之差的多项式,并且新增多个约束条件,故本文模型更加复杂化。考虑到本文计算量较大,依据模型的特点,设计了改进遗传算法,建立了虚拟港口,即若待还租箱在某一港口被再次利用,则经过这一虚拟港口,再多次进行交叉变异,得到精确解。这一过程的具体执行流程图如图2 所示,设计了基于混合整数规划的启发式算法(MATHEURISTIC),即将启发式算法与混合整数规划方法(mixed-integer programming,MIP)集成进行模型求解。

图2 算法流程图

3.1 解的表示

依据船舶的装卸货物量对船舶进行编号,如表1,染色体表示船舶编号。

表1 染色体编码示例

3.2 初始解的生成

基于模型中的约束,设计了如下的初始解生成策略。

初始化参数,生成染色体第一行。具体步骤如下。

步骤1计算染色体中包含优先船舶的各艘船舶的进港时间、重箱运输成本、空箱运输成本及航行时间。

步骤2对于每条航线,若优先船舶的航行时间小于备选船舶的航行时间并进港时间优先,且成本小于紧前船舶,转到步骤5;若优先船舶航行时间大于备选船舶的航行时间,或成本大于备选船舶,转到步骤3;若优先船舶进港时间晚于备选船舶进港时间,且成本小于备选船舶,转到步骤4。

步骤3将优先船舶与紧前船舶的位置互换,转到步骤2。

步骤4重新随机生成染色体并转到步骤1。

步骤5保留此层染色体。

3.3 适应度函数的确定

本文模型的目标函数为运输整体成本最小。目标函数越小,解就越优良,因此,本文的适应度函数为:f(x)=Cmax-r(x),r(x) ＜Cmax,if:f(x)=0,r(x) ＞Cmax,其中r(x)为目标函数,Cmax为本代个体解得目标函数的最大值。

3.4 选择过程

选择是为了选出优秀的个体组成一个新的群体,本文采用轮盘赌选择优秀个体,每个个体i被选中的概率为,具体的选择过程如下。

步骤1计算个体的选择概率,将其进行从小到大的排列。

步骤2按照数组的排列顺序将其累加,第n个数变成前n项之和。

步骤3生成一个0～1 之间的随机数,计算其落到的区间。找到这个区间对应的个体,重复多次,直到产生了一个数量相同的种群。

步骤4按照交叉概率对新种群进行交叉操作,每一个个体与下一个个体概率交叉,直至所有个体遍历完毕。

3.5 实数交叉与变异过程

本文设计了实数交叉算子,即将种群中的第1个染色体m1和第a个染色体ma在j位进行交叉,从而生成新个体,即,其中n为[0,1]区间的随机数,具体交叉变异过程如下。

步骤1生成一个0～1 的随机数,检测该数是否小于交叉概率,若是转到步骤2,否则转到步骤3。

步骤2若该数小于变异概率,则转到步骤5,否则转到步骤4。

步骤3保持这条染色体不变,保留到下一代。

步骤4对此条染色体与相邻的下一条染色体进行实数交叉,将新生成的染色体保存至下一代。

步骤5对此条染色体进行变异操作,具体操作步骤为:任选一条装有待还租箱的船舶,将其随机分配到其他符合船舶容量的运输航线上。

3.7 基因修复算子

在交叉变异生成新个体时,会出现某个场区的待装载集装箱的数量大于船舶容量的情况,采取以下步骤修复。

步骤1依次检查个体,如果某个场区的待装载集装箱的数量大于船舶容量转到步骤2,否则转到步骤3。

步骤2在更多舱位的船舶中随机选取一个基因与之交换位置。转到步骤1。

步骤3输出新个体,经过基因修复的个体,要符合本算法的生成策略,对新个体依照3.1 节的方法来调整。

3.8 算法终止条件

终止条件为计算到预设的最大进化迭代次数时停止,然后输出各代种群中最优的染色体,评价每个染色体的最终得分值,得出最大利润。

4 算例实验

4.1 算例描述

以某内贸航运公司为例,该公司经营的北-南航线的始发港为营口港,依据合同规定,该公司租借的集装箱遵循何地借、何地还的规则。已知始发港为营口港,还箱点所在港口为广州新港,航线示意图如图3 所示。

图3 航线运营网络图

假设各港口装卸效率统一,为150 TEU/h,以及各港口待装货物全部上船,根据模型中船舶的约束,对船舶航线选择进行了计算。在保证货物全部装走的情况下,可优化其船舶调度情况如表2～表10 所示。

表2 船舶编号与实际航线

表3 某内贸船公司船期表

表3 续

表4 船舶容量与适用航速

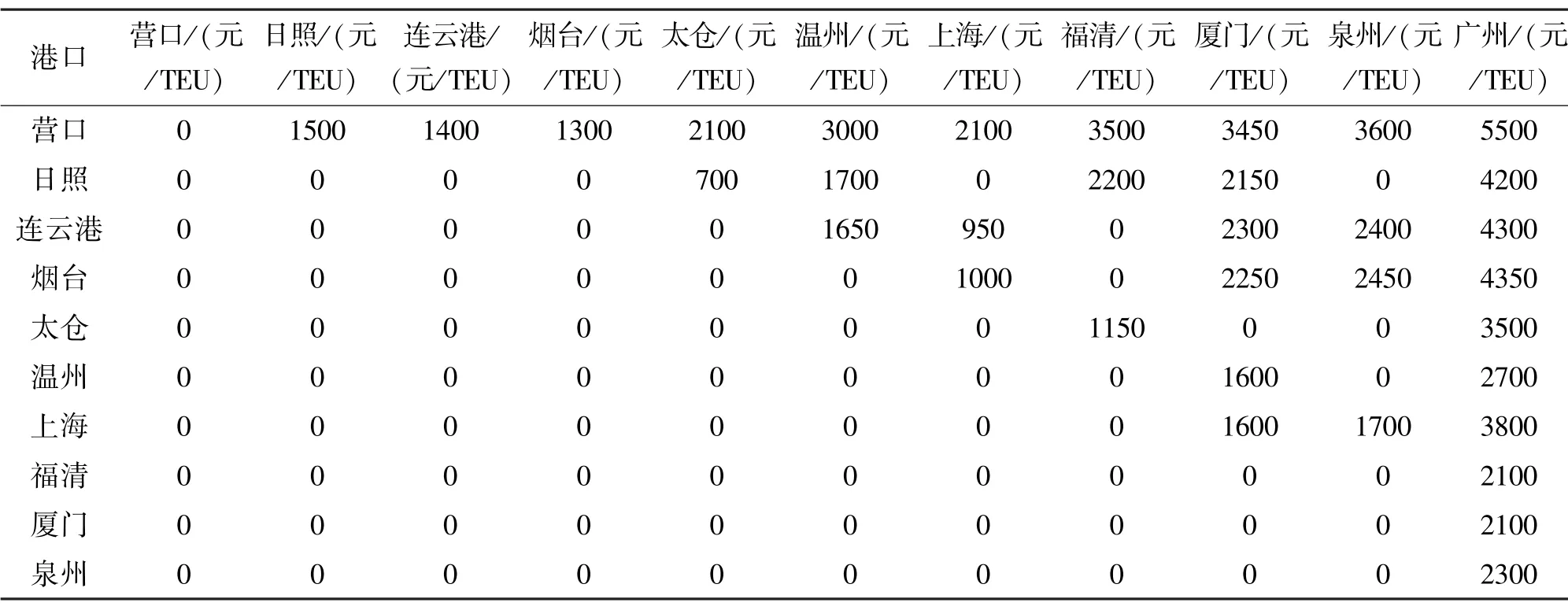
表5 运价表

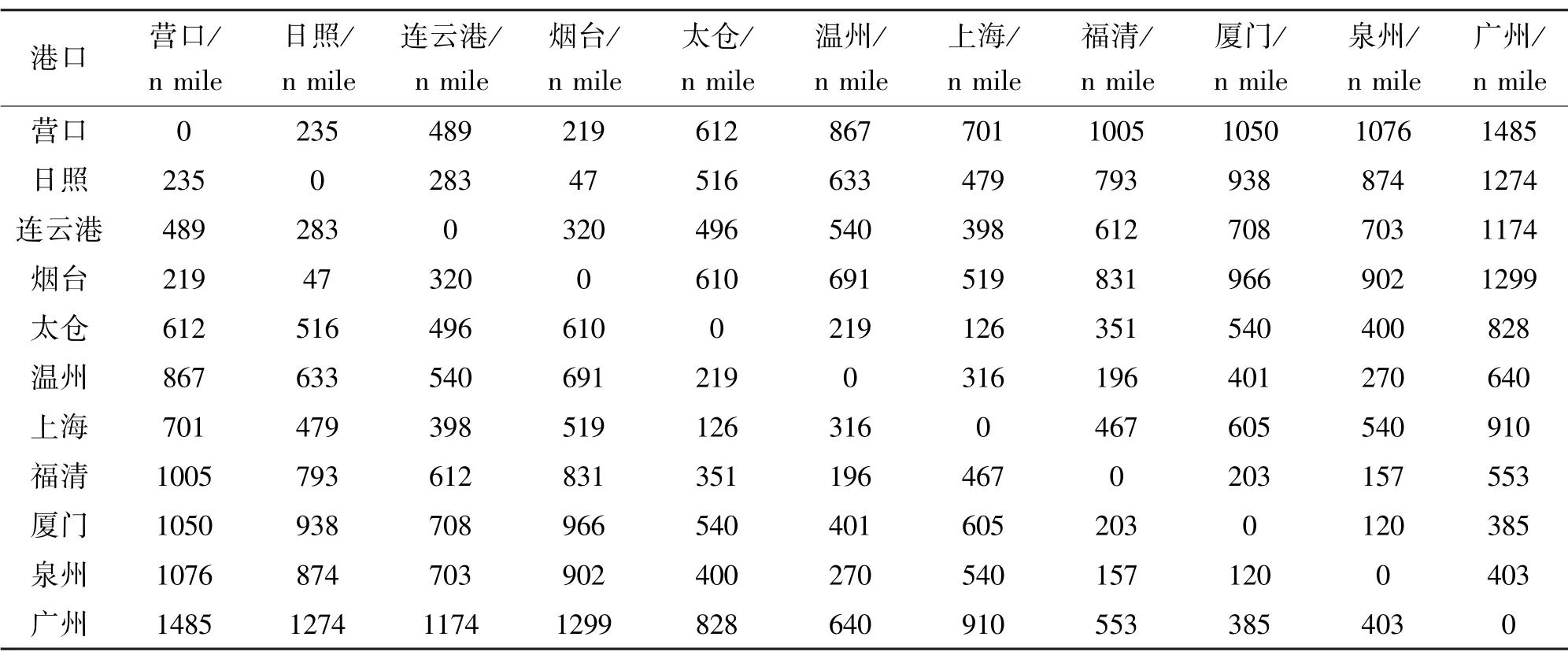
表6 港口间距离

表7 各港口待运货物可装箱量

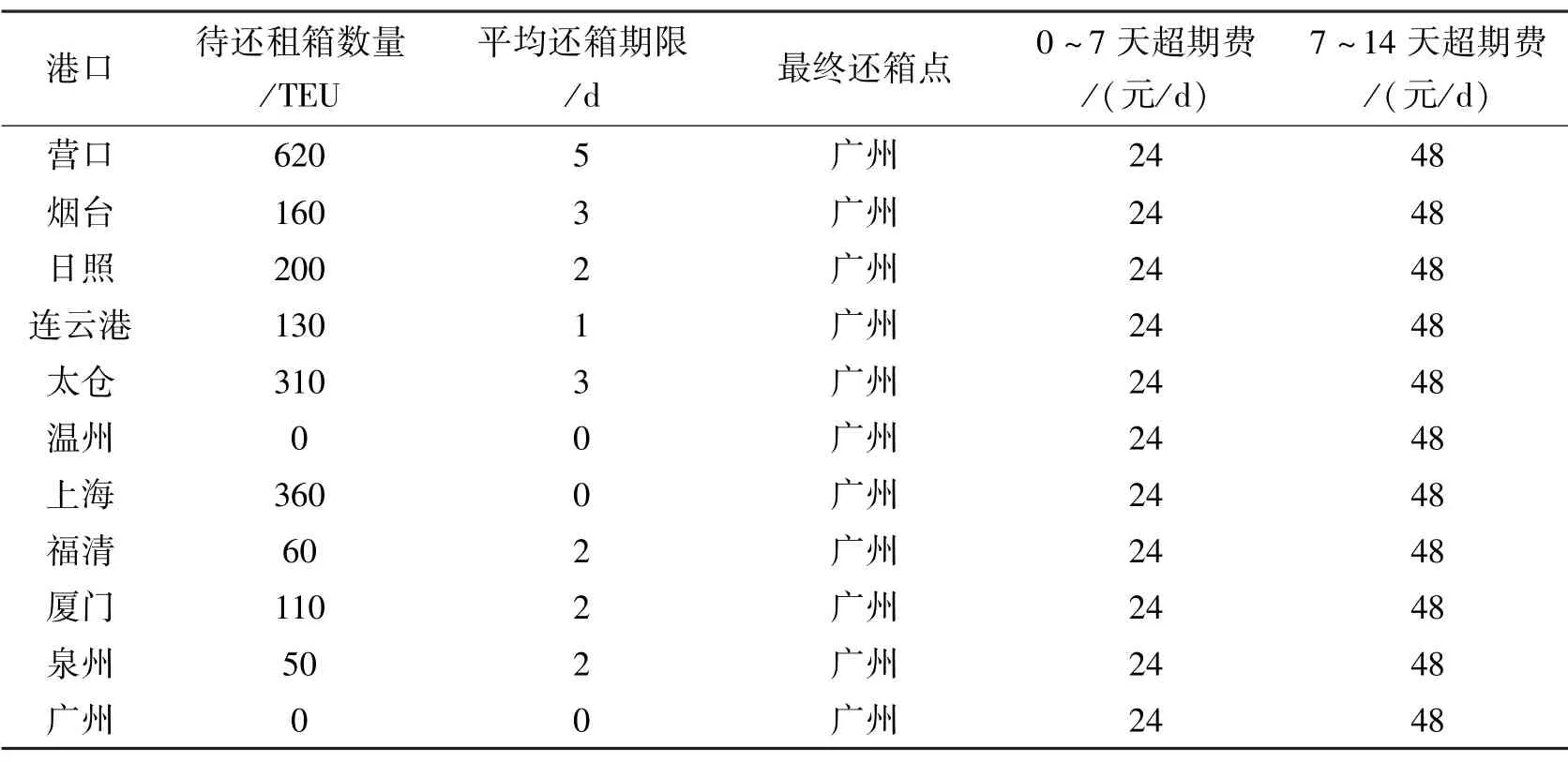
表8 各港口待还租箱数量及还箱截止期限

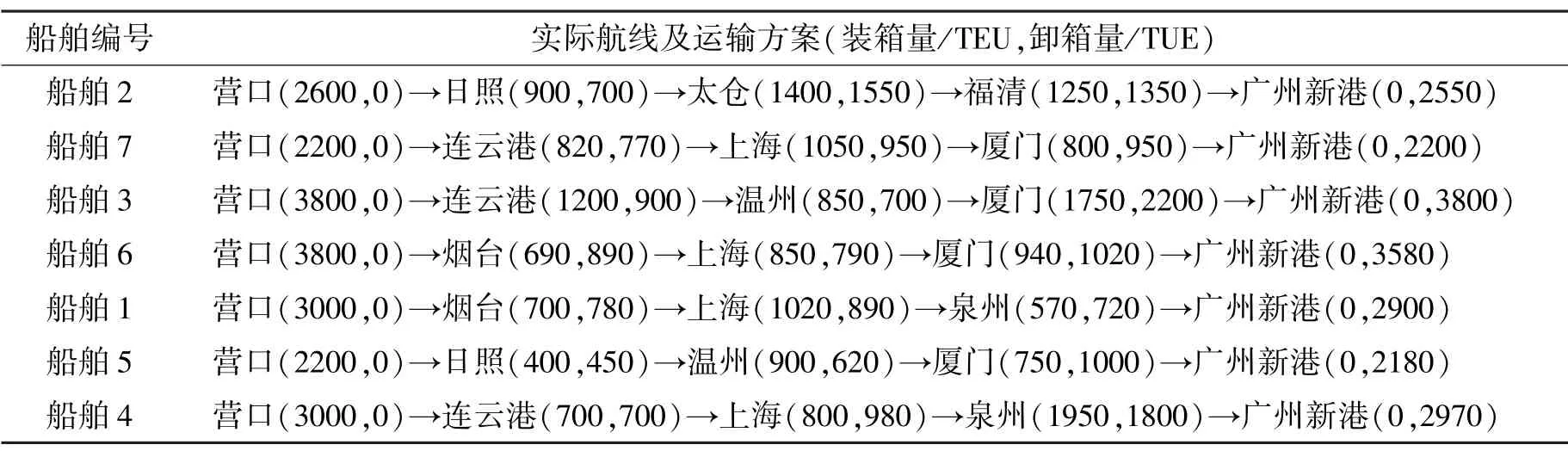
表9 船舶调度情况

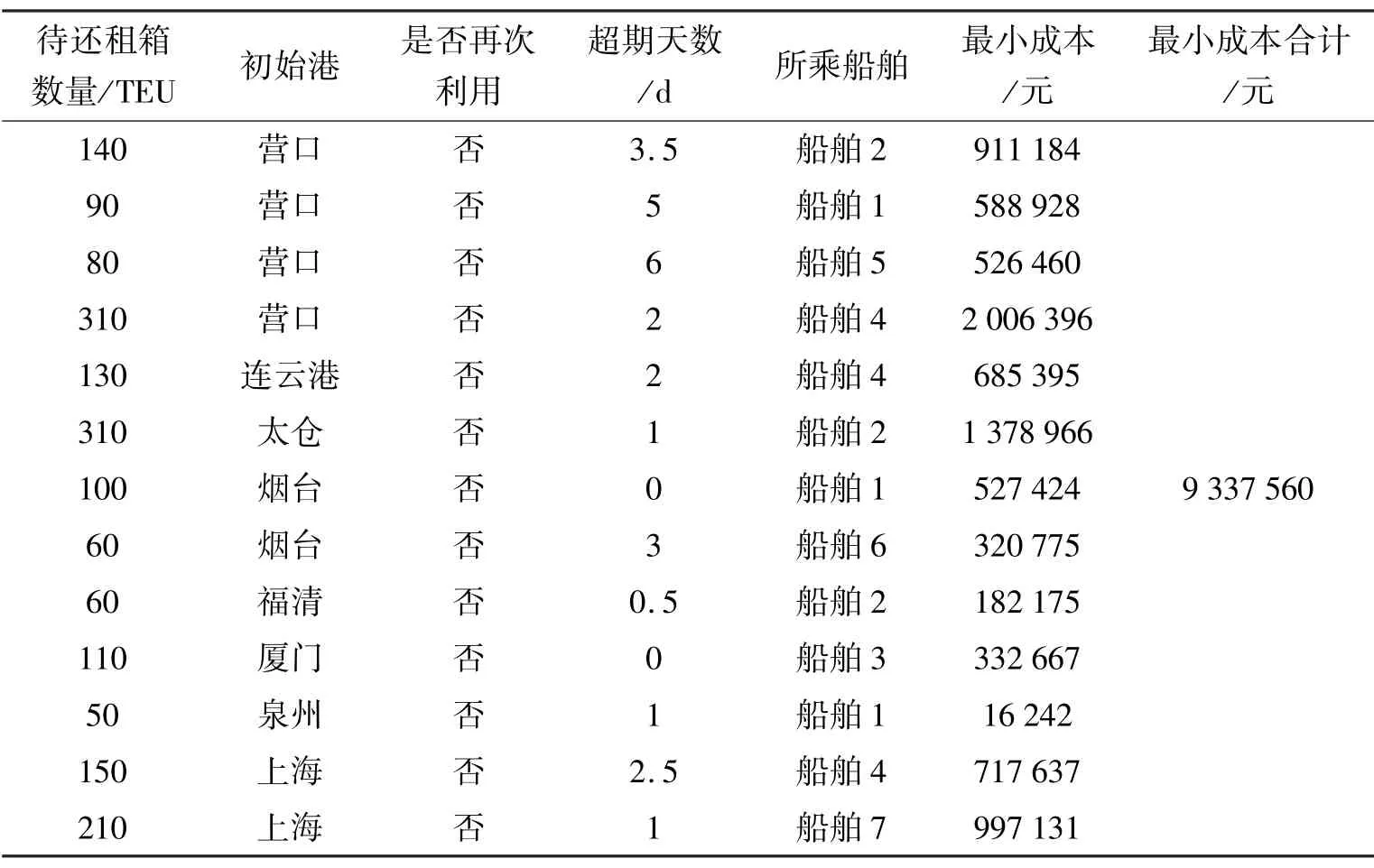
表10 航运企业实际船舶调度成本

因各个港口空箱需求量不同,故本文着重考虑待还租箱再次利用,以减少还箱成本。因此,假设待还租箱运到用箱港口之后,需等下一个周期的船装走,所以超期天数应以租箱第一次上船开始计时,截止到租箱到达还箱点的时间与待还租箱返还期限之差。假设每个集装箱运输成本为60 元/d,各港口停泊及装卸单位成本统一。采用启发式算法与MIP方法集成进行模型求解。各港口待还租箱路径如表11所示,最优方案收敛图如图4。

表11 考虑各港口待还租箱所乘船舶调度成本

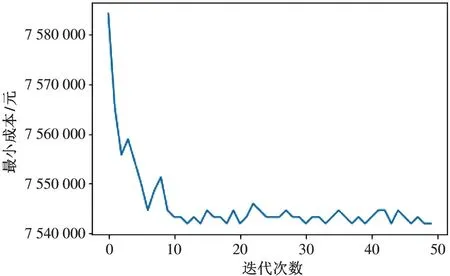
图4 最优方案收敛图

4.2 方案有效性验证

在船舶实际运营的过程中,采用待还租箱再次利用的措施,本周期航线网的运营成本为7 542 460.5 元。通过比较表10 和表11,可看出成本可降低19%,虽待还租箱再次利用会产生额外成本,但所增加的利润可完全覆盖并超出额外成本。另一方面,从长期运营的角度看,待还租箱的再次利用,可在一个或几个周期内减少租箱次数,可有效降低租箱成本,从而验证了本文方案的有效性。

4.3 算法科学性验证

(1)算法有效性

现将本文数学模型用CPLEX 软件求解,因本文数学模型均是线性,故可直接求解。CPLEX 运行时间上限设置为4 h,再与MATHEURISITIC 计算结果进行比较,各组对比结果见表12。

从表12 可以看出,单独利用CPLEX 求解时,用时较长,在求解大规模数据时,短时间内无解。而采用启发式算法与CPLEX 相结合进行求解,不单利用了改进遗传算法计算速度较快的优点,而且也利用了CPLEX 精确求解的优点,得到的最优解的所有偏差值都控制在5%以内。综上,本文采用的算法可有效地在短时间内解决问题。

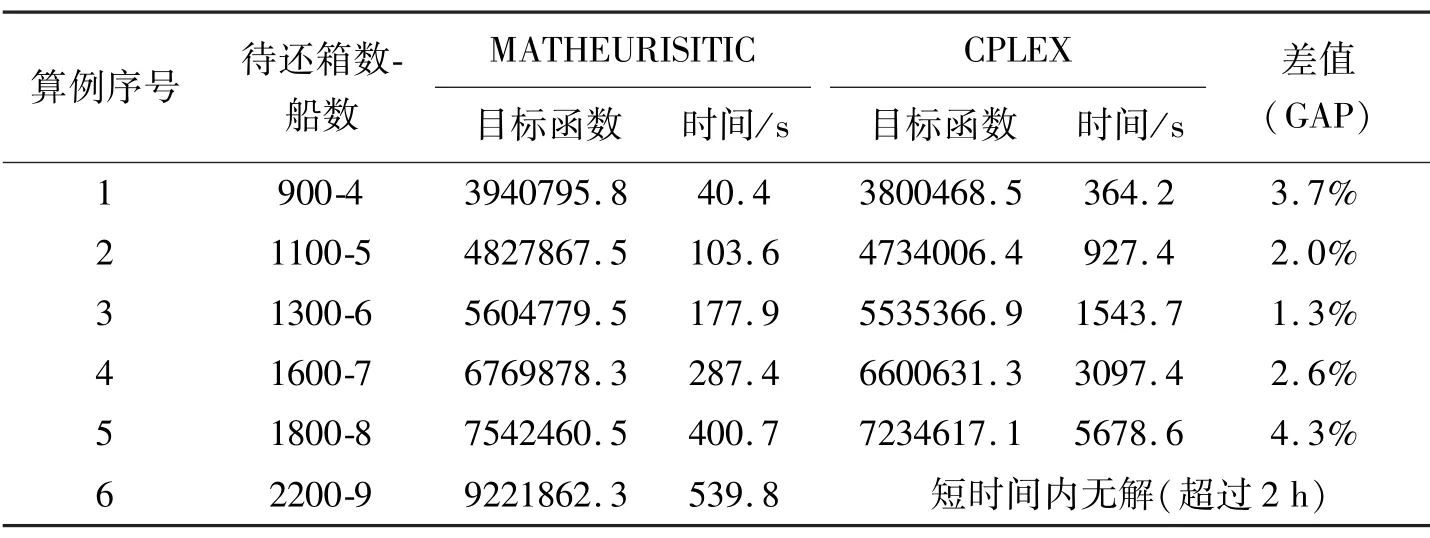
表12 算例比较结果

(2)算法优越性

为验证算法的优越性,本文同时针对此问题,分别用量子差分进化算法(quantum differential evolution,QDE)[13-14]、蚁群算法(ant colony optimization,ACO)、元遗传算法(meta-heuristic algorithm,MHA)[15]进行求解并与本文算法进行比较。QDE参数设定最大迭代次数500,种群规模为200,收缩因子为0.8,量子交叉为0.2;ACO 参数设定最大迭代次数500,种群规模为200;MHA 参数设定最大迭代次数为500,种群规模为200。算法比较结果如表13所示。

其中表13 中QTIC、ATIC、MTIC 分别表示MATHEURISIT 与QDE、ACO、MHA 求解本文问题时所得目标函数值之差占目标函数值的比例,表14 中QTIC、ATIC、MTIC分别表示MATHEURISIT 与QDE、ACO、MHA 求解本文问题时CPU 耗时之差占MATHEURISIT 求解时CPU 耗时的比例。经比较可知,蚁群算法(ACO)和元遗传算法(MHA)计算时间短,但目标函数值相差较大;量子差分进化算法(QDE)计算时间及结果与MATHEURISIT 相近,但速度慢,且结果有偏差,因此,本文算法存在优越性。

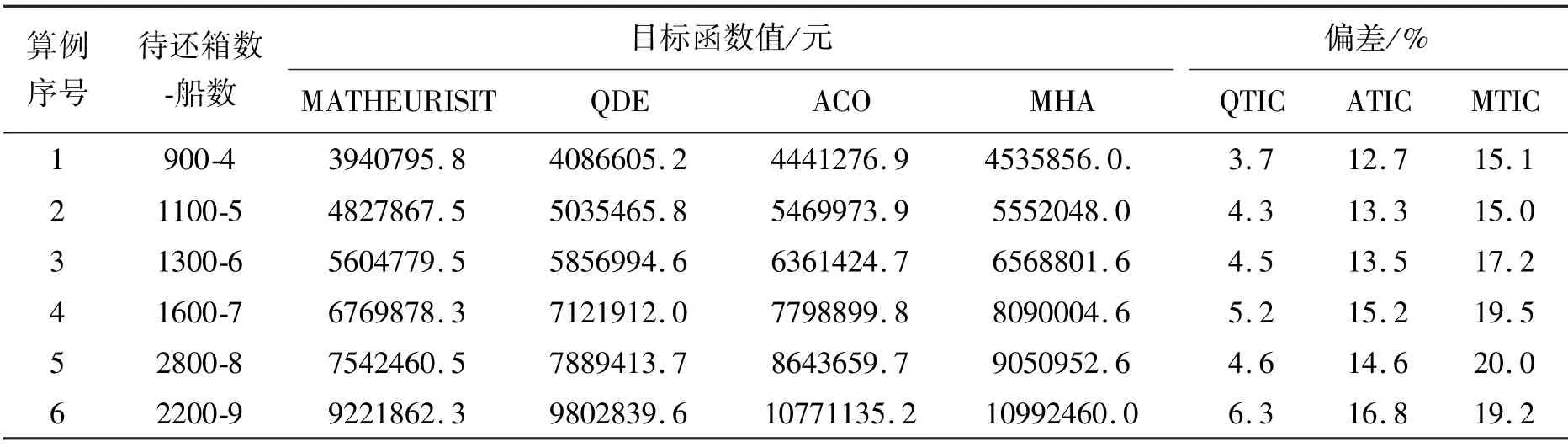
表13 改进遗传算法和其他算法目标函数值比较

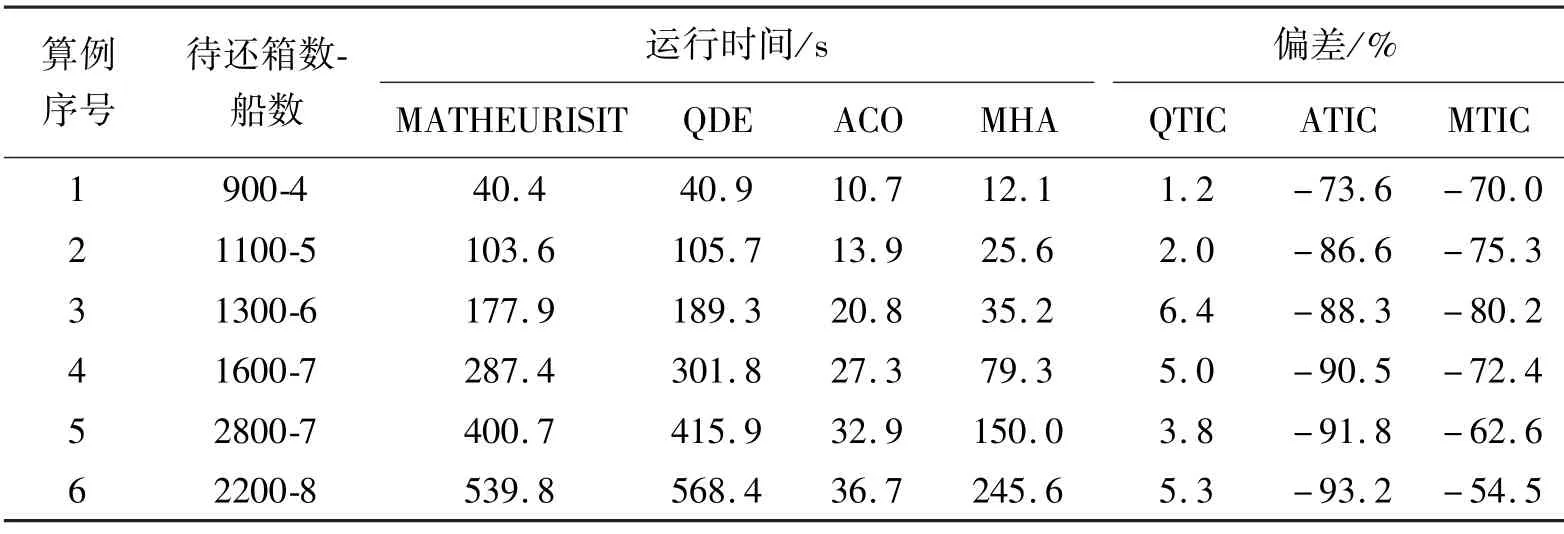
表14 改进遗传算法和其他算法CPU 耗时比较

4.4 灵敏度分析

待还租箱的数量波动会影响船舶航线的规划,从而进一步影响成本。从表15 中可以看出,待还租箱数量上的波动对成本的影响中,前者较后者的成本增加趋势显著。在待还租箱逐渐增加的状态下,选择待还租箱再次被利用,可有效缩小成本。

表15 待还租箱数量变化灵敏度分析

因集装箱超期费是探究租箱是否可以再次利用的关键成本因素,而待还租箱利用率是探究待还集装箱是否可以再次利用的关键利润因素,为了进一步探究待还租箱在返还过程中再次被利用的可行性,本文针对以上两个变量进行了敏感性分析,结果如图5 所示。

图5 还箱成本波动图

通过对比以上两组数据可以看出,超期费率的变化对成本的波动情况影响较小,而待还租箱再次利用所创造的收益随着利用率的增加变化趋势明显。故可在本文的约束条件下,选择待还租箱再次被利用,尽管会产生更多的超期费,但利用此类箱所产生的利润可将其完全覆盖,并缩小其余成本,这也验证了本文研究的有效性。

5 结论

本文以内贸定期航线的航运企业为研究对象,研究在航运企业的实际运营中,租箱返还影响的船舶调度问题。以运输成本最小为研究目标,着重考虑待还租箱的资源利用、船舶航线选择问题,最终给出了各集装箱船舶运输的最优路径以及待还租箱的最优搭载船舶方案,减少了船舶运输成本,表明通过船舶航线的整合以及待还租箱的合理利用可有效降低租箱次数及还箱成本。

结合问题特点,构建混合整数模型,并设计了改进遗传算法与CPLEX 集成进行求解。为类似问题的解决提供了思路。

通过敏感性分析发现,待还租箱数量的波动对船舶运营成本的影响较大,但经过本文优化后的运输方案,可适当降低成本。再次利用率的变动对还箱成本有显著影响,但超期费率的变动影响不大,因此,将待还租箱由空转重或者由重转空所产生的利润与需支付的超期费之差会越来越大,这既可有效减轻直接还箱带来的成本负担,也可减少租箱次数。本研究为航运企业的实际调度决策起辅助支持作用,对于企业的集装箱管理有很强的借鉴意义。