2D 伺服阀电-机械转换器参数实时优化的自抗扰同步跟踪控制①

陈滋凯 李 胜 阮 健 张天聪 陈鹏志

(浙江工业大学特种装备制造与先进加工技术教育部重点实验室 杭州310014)

0 引言

电-机械转换器是电液伺服阀的电-机械转换接口,它将系统输入的电信号转换成机械信号,实现信号的转换和放大。作为电液伺服阀的核心部件,其特性将直接决定整个电液伺服阀的动静态性能。所以电液伺服阀能否进一步发展,扩宽其应用场合将与电-机械转换器的研究现状有着不可分割的关系。目前,电-机械转换器发展趋势主要分为结构优化和应用新型材料等方面[1]。在结构优化上,文献[2]提出了一种基于动圈式音圈电机的高频响直接驱动阀,阀的频宽可达到350 Hz,具有良好的动态性能,但由于结构限制了动圈的散热性,电机在大电流工作时必须采取冷却措施。文献[3]提出了一种耐高压的旋转比例电磁铁结构,基于该结构的电-机械转换器结构紧凑、响应快,频宽约为190 Hz,可用于直接驱动电液伺服转阀。但是该结构形式的比例电磁铁依赖于复杂的激光焊接工艺和昂贵的设备,若降低生产成本又会存在加工精度的问题。在应用新型材料方面,文献[4-6]研制的电-机械转换器是利用智能材料“逆压电效应”完成电-机械转换的,其中文献[4]将多层压电陶瓷驱动器集成到伺服阀中并对其进行实验测试,得到压电驱动伺服阀时间响应为0.9 ms,频宽为284 Hz,性能优于传统伺服阀,适用于高速应用。但是作为电-机械转换器,压电陶瓷材料也会带来行程小、滞环大且高压容易击穿等问题。文献[7]利用形状记忆合金致动器中镍钛诺的“形状记忆效应”工作,但其存在响应速度慢、变形不连续且无法精确控制等缺陷。如上所述,电-机械转换器可以通过改进结构来提高性能,但也会出现新的问题,比如加工工艺变复杂带来成本的提升[8]。此外,将新型材料应用于电-机械转换器的技术还不够成熟,实用性也不强。

随着电液控制技术的数字化,为了便于直接数字控制,2D 伺服阀把步进电机作为电-机械转换器。文献[9]利用步进电机作为电-机械转换器并开发了一种新型的直接驱动数字伺服阀,该阀可以直接由计算机驱动,无需D/A,其结构简单、抗污染能力强。但传统上步进电机以步进的方式工作,使得阀的分辨率有限,工作精度不高。为了提高阀的分辨率,文献[10]采用正弦细分驱动与数字式反馈相结合的控制方式提高了步进电机式电-机械转换器性能和其控制的数字阀的控制精度,但采用细分驱动方式提高阀的分辨率的同时也降低了阀的频响,存在着阀的分辨率和响应速度之间的矛盾[11]。针对上述问题,本文提出了同步跟踪控制算法,该算法通过控制步进电机绕组的电流来控制步进电机内部的旋转磁场从而控制了步进电机的转子位置,实现了转子在任意位置快速精确定位。

在同步跟踪控制中,为了消除电-机械转换器转子跟踪误差,常采用结构简单、技术成熟的比例积分微分(proportion integration differentiation,PID)控制器。但对于复杂的被控对象,尤其是模型未知或慢时变系统,PID 往往难以满足控制系统的性能要求且参数确定困难。自抗扰控制(active disturbance rejection control,ADRC)[12]是一种新型非线性控制器,可以实时估计并补偿系统内外扰动,不依赖于被控对象准确的数学模型,对系统参数的变化不敏感。文献[13,14]成功地将自抗扰控制器应用于电机控制领域,提高了系统的鲁棒性。但是,这些研究常规自抗扰控制器的文献都没有对如何整定控制器参数做说明,而参数整定又是系统设计中的重要步骤,它将直接且显著地影响系统的响应性能。一般情况下,自抗扰控制器都是采用试错的方法调试,这种人工整定参数的过程费时费力且难以获得满意的控制效果。而且根据被控对象不同,参数的取值范围也会相应改变,这限制了自抗扰控制方法的推广和使用,因此有必要找到一种调参方法来解决这一困境。而自适应遗传算法(adaptive genetic algorithm,AGA)[15]适用于求解复杂的优化问题,有并行性、多点寻优、应用方便且易于获得最优解等优点,故本文采用AGA 来对自抗扰控制器参数在线优化。

综上所述,本文提出了2D 伺服阀步进电机式电-机械转换器参数实时优化的自抗扰同步跟踪控制算法,该算法不仅解决了伺服阀分辨率和响应速度之间的矛盾,而且可以提升阀的鲁棒性和抗扰动能力,同时对系统控制器参数进行优化,从而获得了良好的控制效果。

1 参数实时优化自抗扰同步跟踪控制算法

1.1 同步跟踪控制原理

本文将两相混合式步进电机作为2D 伺服阀电-机械转换器。实际上,混合式步进电机从原理上讲是永磁子式同步电动机,因此可以采用同步电机的工作原理实现对该步进电机的同步控制,其工作原理如图1 所示。通过控制两相混合式步进电机A、B两相绕组中的正弦电流、QUOTE 的大小和方向,使它们相位差为π/2,则在步进电机内部就产生一个稳定的旋转磁场θm,转子在θm作用下同步运动并输出角位移θ。故只要能控制步进电机绕组电流ia、ib,就能控制步进电机内部的旋转磁场θm,也就控制了步进电机的转子角位移θ,实现转子在任意位置快速精准定位。

图1 同步跟踪控制原理[16]

1.2 电-机械转换器的数学模型

(1) 电-机械转换器相绕组的电压平衡方程表示为

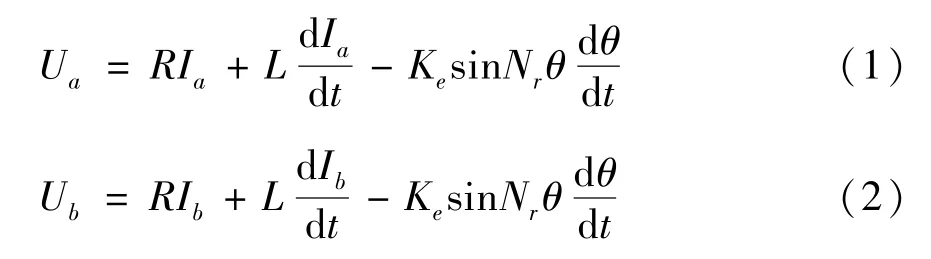
式中,R、Nr、θ分别为绕组电阻、电机齿数、电机转子角位移,L、Ke分别为电感系数和电机绕组的反电动势系数,Ia、Ib分别为绕组a、b的电流,Ua、Ub分别为绕组a、b的电压。

(2) 电-机械转换器输出电磁力矩为

式中,Tm为绕组产生电磁力矩的峰值,θm、θ分别为理论旋转磁场的角位移和电机转子角位移,Nr为电机齿数。

(3) 电-机械转换器转子动力学方程为

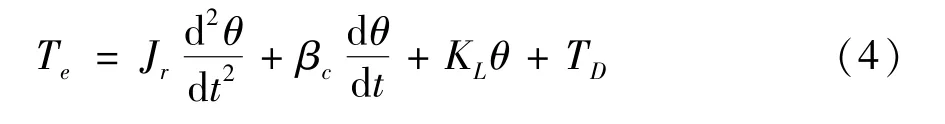
式中,TD为电机负载转矩,KL为电机外加弹性刚度,βc为电机摩擦阻尼系数,Jr为转子等效转动惯量。

式(1)～(4)构成了电-机械转换器的数学模型。

1.3 实时优化自抗扰同步跟踪控制算法

为了提升电-机械转换器性能,保证其转子在任意角位置实现精准快速的定位并避免转子位置受到电-机械转换器内部参数变化以及外界负载波动等扰动的影响,结合前述同步跟踪控制原理,本文提出步进电机式电-机械转换器参数实时优化的自抗扰同步跟踪控制算法,算法框图如图2 所示。这是带有前馈控制的双闭环控制算法,主要由ADRC 位置控制器、前馈补偿、失调角限制、电流闭环和AGA 在线优化模块等组成。

图2 虚线框内是AGA 在线优化算法,其主要利用电-机械转换器的转子角位移θ(t) 输出特性对电-机械转换器位置闭环ADRC 控制参数进行评估并在线实时优化。每当系统工作环境或结构参数发生变化时,由该算法在线实时给出的控制参数总能使系统取得最优的控制性能。同时,该算法也解决了人工整定ADRC 控制器参数费时费力的问题,其还可对绕组电流闭环PI 控制器参数同步进行优化以获得更好的闭环反馈控制品质。

图2 参数实时优化的自抗扰同步跟踪控制算法框图

算法最外环的位置闭环是为了确定步进电机内部所需要的理论旋转磁场θm,从而控制电-机械转换器的转子位置θ(t),使其在输入控制信号θi(t)作用下在任意位置快速精确定位。由于步进电机是一种非线性时变系统,根据前述二阶数学模型,该位置闭环采用鲁棒性更好的二阶ADRC 位置控制器,其能估计出作用于系统的除控制量之外的加速度部分的扰动并补偿,而一阶ADRC 只能估计到速度部分的扰动。二阶ADRC 位置控制器不仅可以保证电-机械转换器在电感、摩擦力等内部参数变化、外部负载干扰及系统工作压力波动等干扰下仍有良好的控制效果,而且减少了步进电机的磁滞和磁饱和等非线性因素对电机转子输出特性的影响。

考虑到位置闭环的作用是消除转子位置和输入信号的跟踪误差,消除失调角,而电机转子的运动又必须由失调角来牵引,故引入前馈控制,让其与位置控制器的输出共同确定所需要的理论控制磁场θm(t)。

当失调角大于π 时,电机开始处于不稳定的位置并出现失步现象。为了防止失步现象发生,需要对转子位置θ(t) 实时跟踪,并通过限制理论旋转磁场θm(t) 使失调角在±π(半个齿距角)之间。

算法内环是电流闭环,主要是为了控制两相绕组的实际电流iaf、ibf(通过电流传感器检测得到)从而控制其所产生的实际旋转磁场,保证步进电机内部实际旋转磁场与所需的理论旋转磁场θm′(t) 相一致,从而保证转子的同步跟踪运动。其中,电流闭环的理论控制电流ia、ib是根据θm′(t) 分解得到的。

综上并根据同步跟踪控制原理,电-机械转换器控制流程如下。首先,理论转子角位移信号θi(t)和步进电机实际转子角位移信号θ(t) 通过AGA 优化的二阶ADRC 位置控制器运算后产生理论控制磁场θm(t),该信号在失调角限制下再经电流分解产生电机两相绕组理论控制电流ia、ib;然后将ia、ib和步进电机两相绕组实际控制电流iaf、ibf相比较产生的偏差信号经AGA 优化的PI 控制器运算后产生SPWM 占空比信号,该信号通过控制驱动电路中开关管和功率管的工作状态来控制实际绕组电流和其产生的旋转磁场;最后完成对电机转子转角位置的精确控制。

2 ADRC 位置控制器设计

ADRC由跟踪-微分器(tracking differentiator,TD)、扩张状态观测器(extended state observer,ESO)和非线性反馈控制律(nonlinear state error feedback,NLSEF)构成。这三部分可以有多种不同的组合形式,本文针对电-机械转换器的二阶数学模型,综合考虑了控制精度、响应速度等多方面性能因素,采用了二阶ADRC 控制器,结构框图如图3 所示,其中M为被控电-机械转换器。

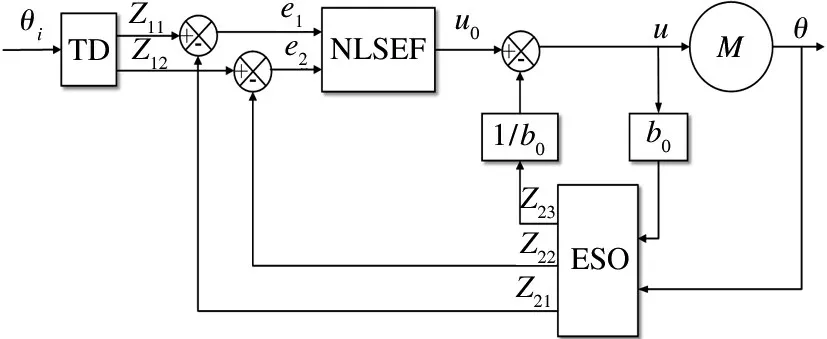
图3 二阶位置自抗扰控制器结构框图

2.1 跟踪-微分器设计

为了避免电机系统在阶跃信号的直接作用下产生振荡,用TD 来对输入控制信号θi(t) 进行改造,其输出Z11将在短时间内跟上阶跃信号来实现过渡,同时给出跟随过程的微分信号Z12,TD 形式如下:

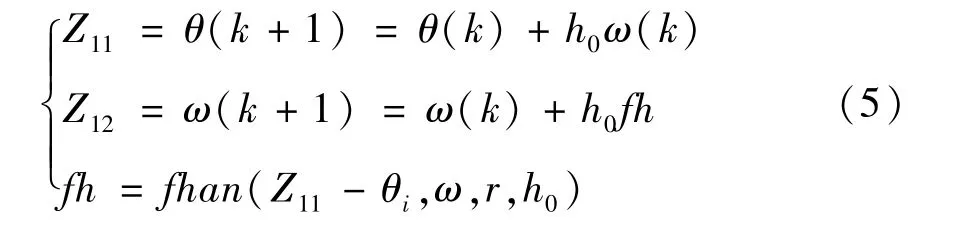
式中,θ为电机转子角位移信号,ω为角速度信号,Z11、Z12分别是θ和ω的跟踪信号,r为跟踪速度因子,h0为控制器滤波因子,k为时间t与时间步长的比值,函数fhan表达式为

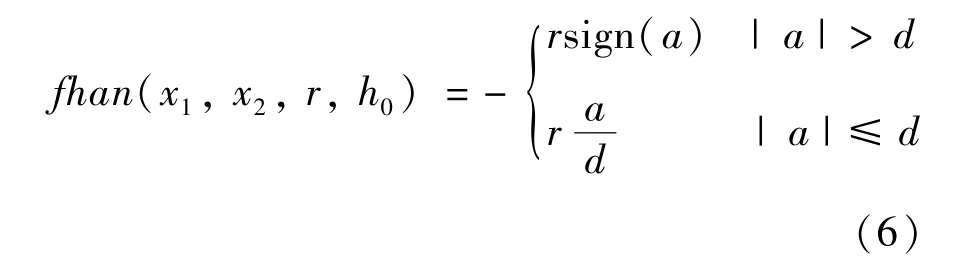
其中a的表达式为

式中,d=rh0,d0=h0d,y=x1+h0x2,a0=

2.2 扩张状态观测器设计

为了观测电-机械转换器的角位移信号、角速度信号及扰动信号并实时反馈和补偿,设计了ESO,它是整个自抗扰位置控制器的核心部分,其性能将直接影响ADRC 控制器的性能,表达式为

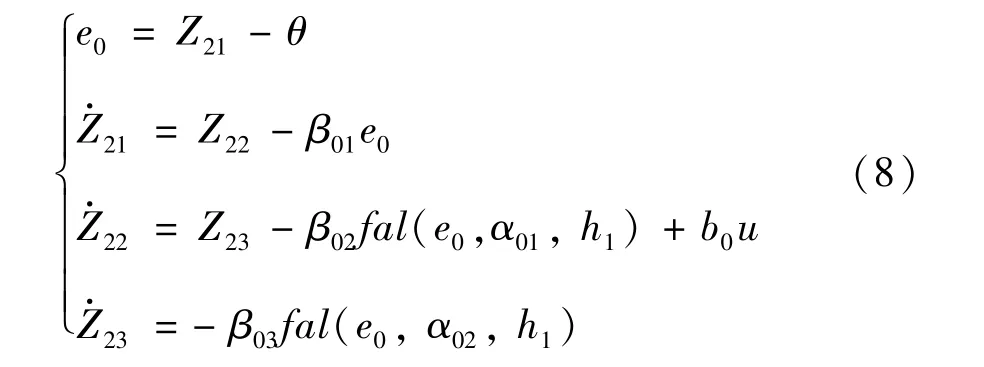
其中非线性函数fal(e,α,h) 的定义为

式中,Z11、Z12和Z13分别为ESO 对电机实际角位移θ(t)、角速度ω(t) 以及总和扰动的观测值,β01、β02、β03是误差校正增益,α01、α02、h1是非线性参数,e0是状态变量误差。

由于ESO 的设计是关键部分,为了减轻ESO 运算负担,减少控制器CPU 的存储容量并缩短信号处理时间,同时使电机扰动估计更准确,补偿更到位,完成对电机的实时控制,本文根据电-机械转换器的已知模型,将电机转子动力学方程用二阶ADRC 控制对象模型表示,得到电-机械转换器的总和扰动,无需再根据系统的输入信号、状态变量和特殊的非线性效应去估计作用于系统的加速度的实时作用量(扰动),推导过程如下:

式中,u为系统控制量,b为u的系数,f(θ,ω) 为系统总扰动。根据式(4)和式(10),将电-机械转换器数学模型转化为

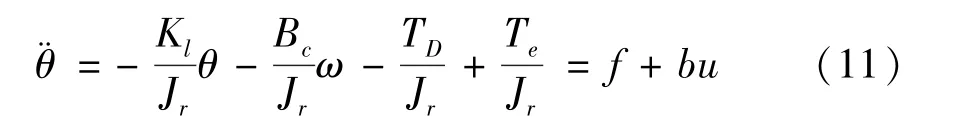
,Te是电-机械转换器输出电磁力矩。

2.3 非线性反馈控制律设计

为了提高ADRC 的动态性能和鲁棒性,设计了NLSEF,仅用一个简单的非线性函数的数学拟合即可完成,表达式如下:

式中,α1、α2、h2是非线性参数,β1、β2为非线性误差反馈增益参数。

3 基于AGA 的ADRC 和PI 参数优化设计

本文提出的实时优化自抗扰同步跟踪控制算法中,AGA 主要完成对ADRC 位置控制器中ESO 的误差校正增益β01、β02、β03,NLSEF 的反馈增益β1、β2及PI 控制器中的比例增益kp1、kp2,积分增益ki1、ki2的优化。图4 为ADRC 与AGA 参数交互路径示意图。

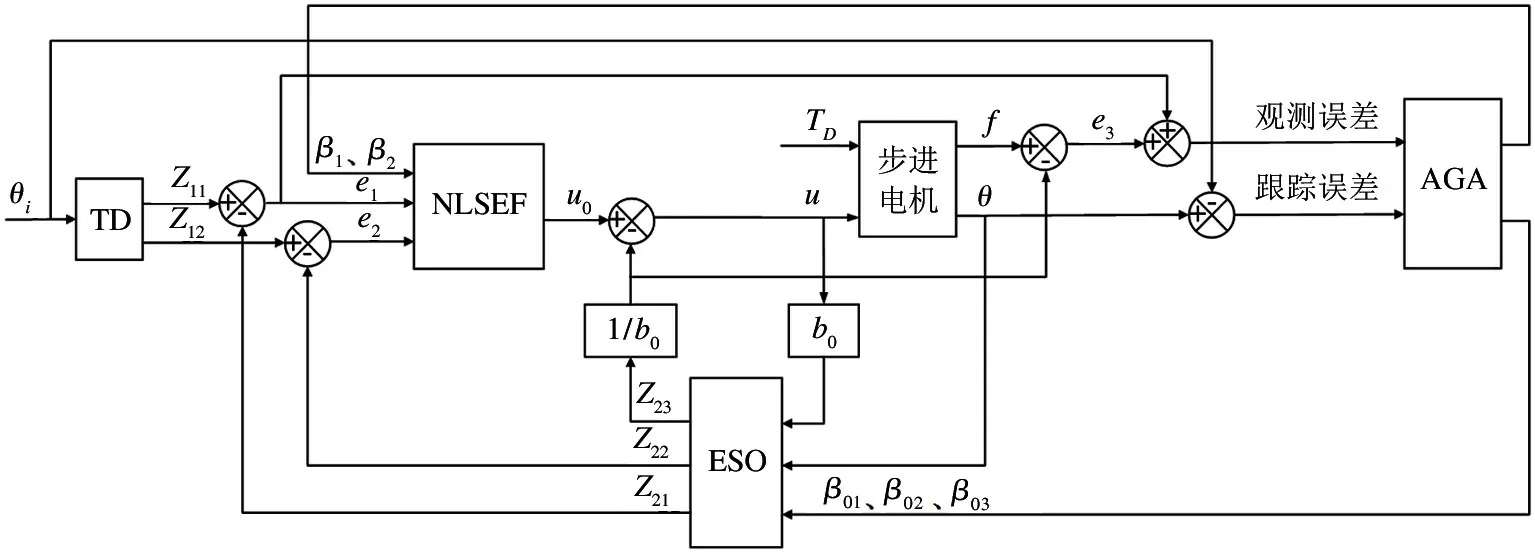
图4 ADRC 与AGA 参数交互路径示意图

如图4 所示,为了使ESO 观测值尽可能接近系统的实际状态,设定AGA 优化目标为提高ESO 的跟踪精度,通过设计一个求观测误差最小值的目标函数J来实现:

其中,e1、e3分别是ESO 观测的位置和总和扰动的误差,权重w1、w3分别为0.7 和0.3。

AGA 工作时不断利用JESO对ESO 性能进行评估并根据自适应遗传机制运算得到最优ESO 参数β01、β02、β03。在AGA 开始前,需预设ESO 误差校正增益β01、β02、β03的遗传代数Gen=100 和种群规模N=60。工作流程如下所述。

(1) 编码和初始化。对参数β01、β02、β03进行实数编码,并设定取值范围分别为[800,1600]、[50 000,55 000]、[1 450 000,1 500 000]以保证ESO稳定,根据随机函数产生初始种群[βa0、βb0、βc0],规模为N×3。

(2) 在AGA 进化机制中,往往以大的适应度值作为优秀基因的评定标准。在式(13)中,目标函数追求最小值的运算,若把JESO放在分母中的子项构造适应度函数F,就可以转化为追求最大适应度值的运算,进化得到的最大适应度值对应的个体编码值即为ESO 参数β01、β02、β03的最优解。F的表达式为

其中,ε取一个较小的实数,目的是避免除零运算。

计算适应度值操作,先用F求出种群中每个个体的适应度值feve,然后计算出当代种群中平均适应度值favg、最大适应度值fmax和要交叉的两个体之间更大的适应度值fb。

(3) 选择和自适应遗传操作。用轮盘赌算法(个体被选中的概率与其适应度大小成正比)选择出当代种群中的优良个体,再根据自适应交叉概率Pc,从选出的优良父代个体中再选两个个体进行单点交叉,然后根据自适应变异概率Pm对交叉后的个体进行变异操作即可得到新一代种群[βa1、βb1、βc1]。自适应交叉概率Pc和自适应变异概率Pm表达式如下:

式中,Pc1=0.9,Pc2=0.6,Pm1=0.1,Pm2=0.01。

(4) 判断终止条件。遗传代数达到设定值时,结束AGA,得到参数β01、β02、β03的最优值。否则,返回步骤(2)循环执行直到AGA 结束,全局收敛。

进化过程中,β01、β02、β03种群中的最大适应度值fmax与进化代数的关系如图5 所示。

图5 β01、 β02、 β03的fmax与进化代数关系图

同理,为了获得更好的闭环反馈控制品质,还需用AGA优化NLSEF和PI控制参数,由于该优化工作同AGA 优化ESO 的主要步骤相同,这里不再赘述,仅对有区别的目标函数设计部分进行简述。在优化NLSEF 和PI 控制参数时,需考虑到电-机械转换器的动态性能对电液伺服阀的重要性。为了追求系统优良的动态性能,应让电-机械转换器输出的转子角位移θ与输入的控制信号θi(t) 的误差尽可能小,故以工程中应用最广泛的时间乘绝对误差积分准则(integrated time absolute error,ITAE)作为目标函数J,并做求最小值的运算,J的表达式为

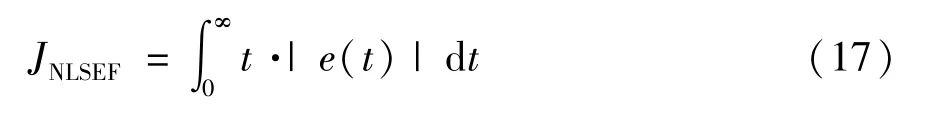
式中,e为电-机械转换器输出的转子角位移θ与输入的控制信号θi(t) 的误差,按此准则设计的控制系统,不仅动态特性好而且瞬态响应的振荡小。同样还需将其作为子项以式(14)的形式构造适应度函数,然后通过AGA 运算得到最优的NLSEF 参数β1、β2和最优的PI 控制参数kp1、kp2、ki1、ki2。

AGA 优化ESO 工作流程图如图6 所示。

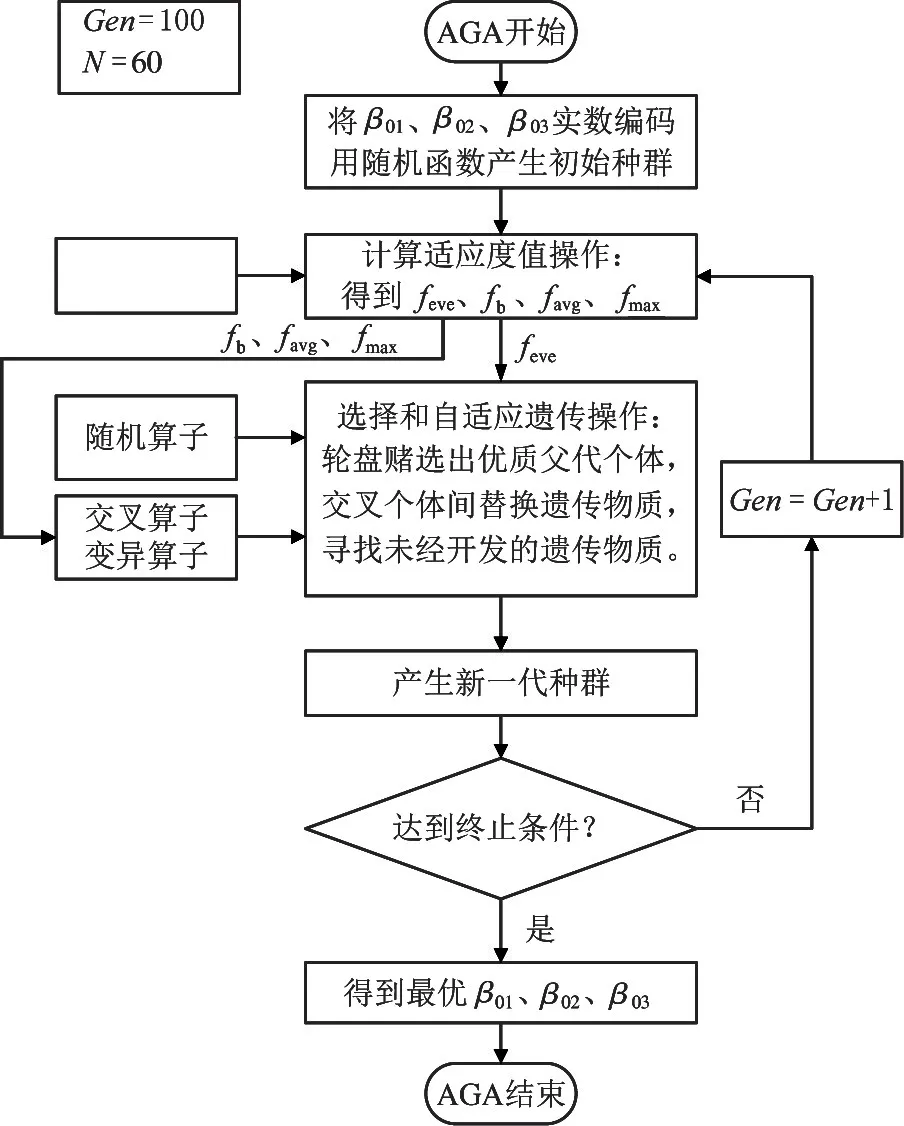
图6 AGA 优化ESO 工作流程图

4 仿真分析

为了验证本文所提方法的有效性,先根据电-机械转换器(FL28STH45-0674B)样机参数设置了Matlab/Simulink 的仿真参数,然后用传统PID 算法和基于AGA 的ADRC、PI 算法(AAP 算法)分别控制电机并对控制效果进行对比分析。表1 为电-机械转换器各项参数,表2 为经AGA 运算后得到的电-机械转换器控制器最优参数。

表1 两相混合式步进电机参数

表2 电-机械转换器控制器最优参数

4.1 时域分析

4.1.1 静态特性分析

在阀满开口幅值条件下,输入一频率为0.1 Hz的正弦波控制信号,得到电-机械转换器的输出信号,过程如图7 所示。然后根据输入、输出的关系得到输入-输出特性如图8 所示。

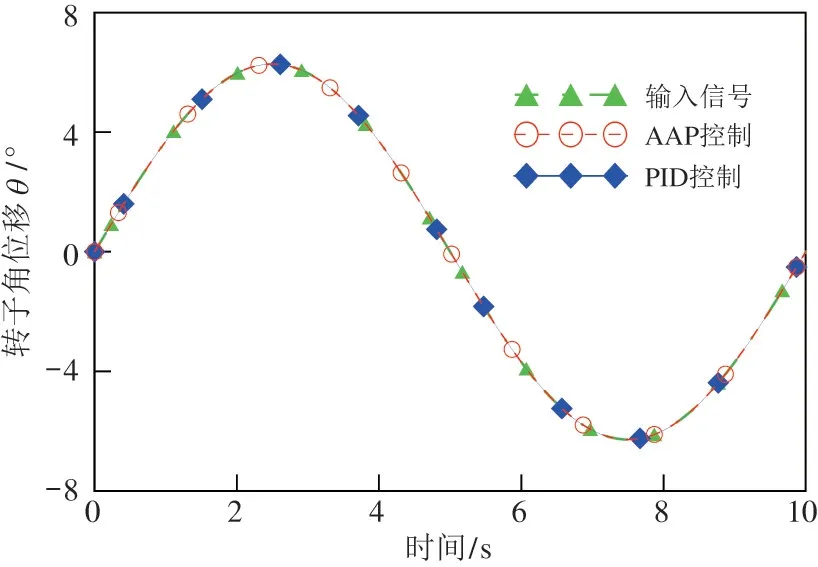
图7 0.1 Hz 下电-机械转换器的输出特性

图8 电-机械转换器的输入-输出特性

图7 和图8 表明在0.1 Hz 下,两种控制算法的输出都很好地跟随输入信号,且滞环和非线性度几乎为0,具有很好的静态特性。

4.1.2 动态特性分析

阶跃响应的上升时间是衡量电-机械转换器动态性能的一个重要指标,在阀满开口幅值阶跃信号的作用下,得到其响应曲线如图9 所示。

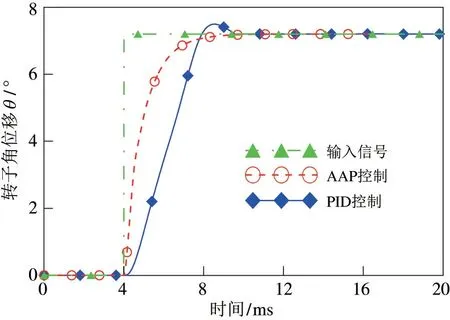
图9 阶跃响应

从图9 可以看出,电-机械转换器在PID 控制时,阶跃响应的上升时间为3.4 ms,出现小幅度的超调现象,而其在AAP 算法控制时,上升平稳无超调,且具有更快的响应速度,上升时间为2.6 ms。

4.2 频域分析

根据电-机械转换器在不同频率的25%阀满开口幅值正弦信号控制下的频率响应,得到其频率特性如图10 所示。

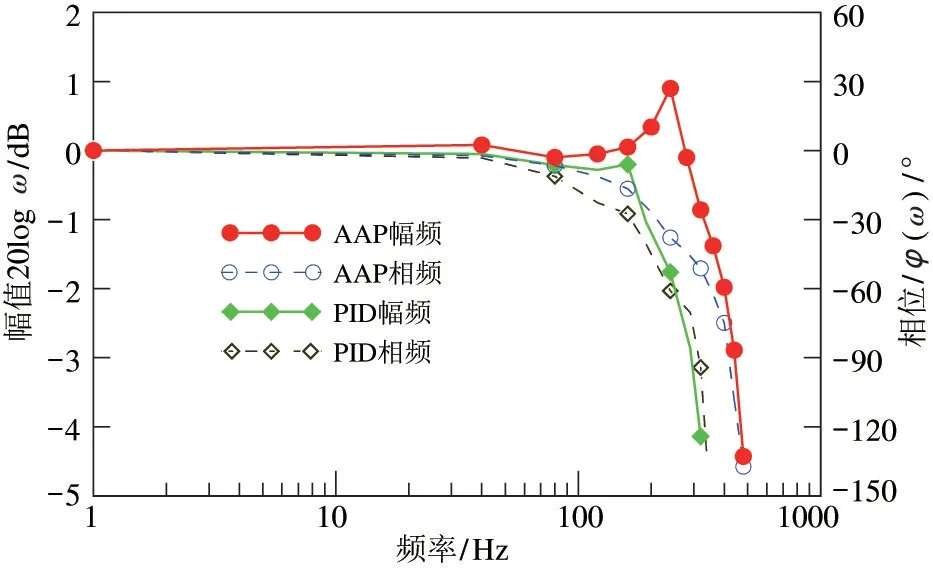
图10 频率特性

从图10 可以看出,电-机械转换器在PID 控制时,对应-3 dB、-90 °的截止频率为290 Hz,而在AAP 控制下的截止频率为410 Hz,可见采用AAP 算法的电-机械转换器具有更大的频宽,频率特性提升显著。

4.3 内部参数变化下系统鲁棒性分析

其他条件不变,仅将电-机械转换器的电感参数增大至20 mH,然后输入阀满开口幅值的阶跃信号,得到第1 组响应曲线如图11 虚线部分所示。同理,仅将电-机械转换器的内部总摩擦力参数增大至3 kg·cm/s2,输入阀满开口幅值的阶跃信号得到第2 组响应曲线如图11 实线部分所示。

图11 电-机械转换器内部参数变化后的阶跃响应

从图11 可以看出,电-机械转换器若受到内部电感变化的干扰,用PID 控制时,其阶跃响应的上升过程出现了抖动及超调加剧的现象,上升时间为4.7 ms,延缓了1.3 ms;而用AAP 算法控制时,电机的阶跃响应不仅上升平稳,而且上升时间为3.2 ms,仅延缓了0.6 ms,受电感变化影响较小。从图11 还看出,电-机械转换器若受到内部摩擦力变化的干扰,用PID 控制时,其阶跃响应的上升过程仍会受到严重影响,上升时间为6.7 ms,延缓了3.3 ms;而用AAP 算法控制时,电机的阶跃响应上升时间为3.9 ms,仅延缓了1.3 ms,受总摩擦力变化影响较小。

综上所述,电-机械转换器在电感、摩擦力这些内部参数变化时,传统PID 算法的动态控制会受到严重影响,存在上升过程不稳定和超调量增大的情况,同时响应速度也受到严重影响;而本文提出的AAP 算法不仅能减轻电机电感、摩擦力变化给控制带来的影响,而且其控制下的电-机械转换器,动态性能依旧良好,具有优异的鲁棒性。

4.4 抗干扰特性分析

在电-机械转换器实际工作过程中,其外部负载并非为固定值,甚至可能出现与理想偏差很大的情况,这些变化对于系统而言是严重的干扰,故本文又对电机受到外部负载干扰的情形进行仿真分析。首先在电机负载端添加一个力矩为4 N·cm 的连续脉冲干扰信号,然后在系统输入端输入一个25%阀满开口幅值的恒定信号,得到电-机械转换器的抗干扰特性曲线如图12 所示。

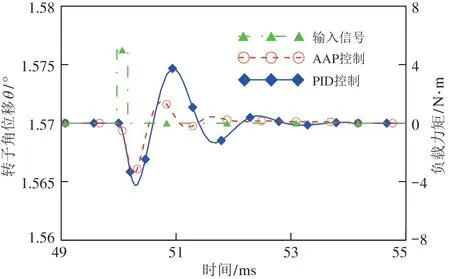
图12 抗外部负载干扰实验局部图

从图12 可以看出,在抗外部扰动实验中,电-机械转换器在两种不同算法控制下,其转子角位移都能在短时间内跳动4 次尖峰后再次稳定且都没超过系统稳态值的±1%,但在AAP 算法控制下,电机输出尖峰值仅为PID 控制下的65%,而且在2 次跳动尖峰后就已经基本稳定,显然,AAP 算法对扰动的抑制效率更高,具有更优异的抗外部扰动特性。

5 实验研究

5.1 电-机械转换器静动态特性及抗扰动特性测试

图13 是电-机械转换器实验平台。信号发生器输出静态特性实验和频率特性实验所需的正弦信号、阶跃响应所需的方波信号;控制器是根据电机控制原理设计的DSP 嵌入式控制器,既用来采集来自信号发生器的控制信号,也实时接收固定在电机上的转子角位移传感器的信号,同时在实验时会保存信号,在实验结束后将信号送于工控机处理。

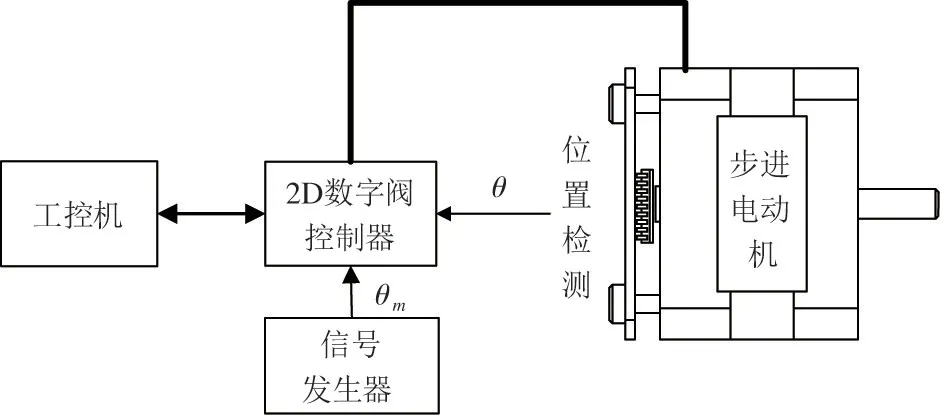
图13 电-机械转换器实验平台

电-机械转换器在0.1 Hz 正弦信号控制下的输入-输出特性如图8 所示呈线性关系,看出其具有良好的静态特性;电-机械转换器的阶跃响应曲线如图14实线部分所示,电感变化后的响应曲线如图14虚线部分所示。后者实验时控制其他条件不变,在两相绕组上各串联一个10 mH 电感再接入DSP 控制器电流输出端口。图15 是电-机械转换器频率特性。

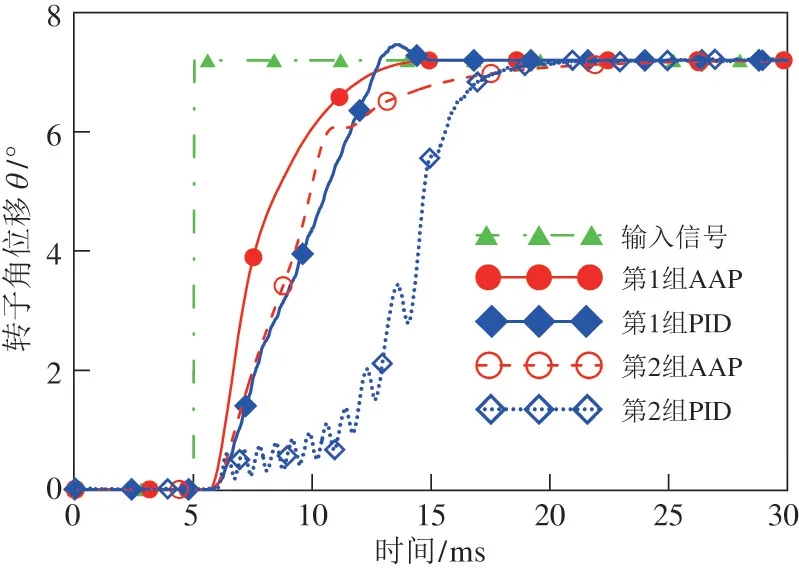
图14 电感参数变化前后的阶跃响应

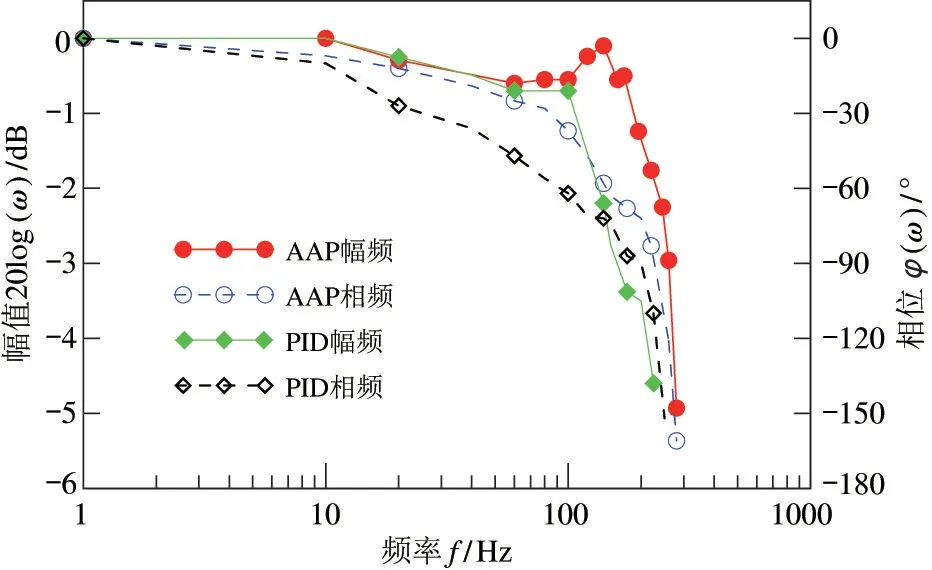
图15 电-机械转换器频率特性

从图14 可以看出,电-机械转换器在PID 控制时,阶跃响应的上升时间约为5.6 ms,出现超调;而采用AAP 算法控制时,上升时间为4.4 ms,且上升平稳无超调。在电感变化后,AAP 算法控制的阶跃响应上升时间为6.4 ms,比PID 控制的8.2 ms 快且稳定,更没有震荡,可知其在电感扰动时具有更好的扰动抑制能力,与仿真结果基本吻合。

从图15 可以看出,电-机械转换器在PID 控制时,对应-3 dB、-90 °处的频宽约为170 Hz,而在AAP 算法控制时,频宽增大42%至240 Hz。虽然在实验中不可避免电机的涡流和磁滞效应等因素造成实验结果低于仿真结果,但显然AAP 控制的电-机械转换器频率特性得到改善,具有更好的动态特性。

5.2 2D 伺服阀频率特性及抗扰动特性测试

图16 为2D 伺服阀性能测试实验平台示意图,在电-机械转换器实验平台基础上增加了液压加载子系统、阀体、示波器、激光位移传感器和压力传感器。其中,激光位移传感器检测阀芯的轴向位移,压力传感器检测系统压力,示波器用于显示和保存输入控制信号和阀芯位移信号。

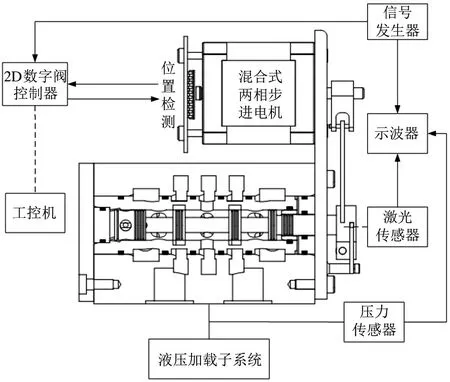
图16 2D 伺服阀实验平台

图17 是实验测得的2D 伺服阀的阶跃响应。图18 是2D 伺服阀的频率特性。图19 是2D 伺服阀抗系统压力扰动特性曲线。

图17 2D 伺服阀的阶跃响应

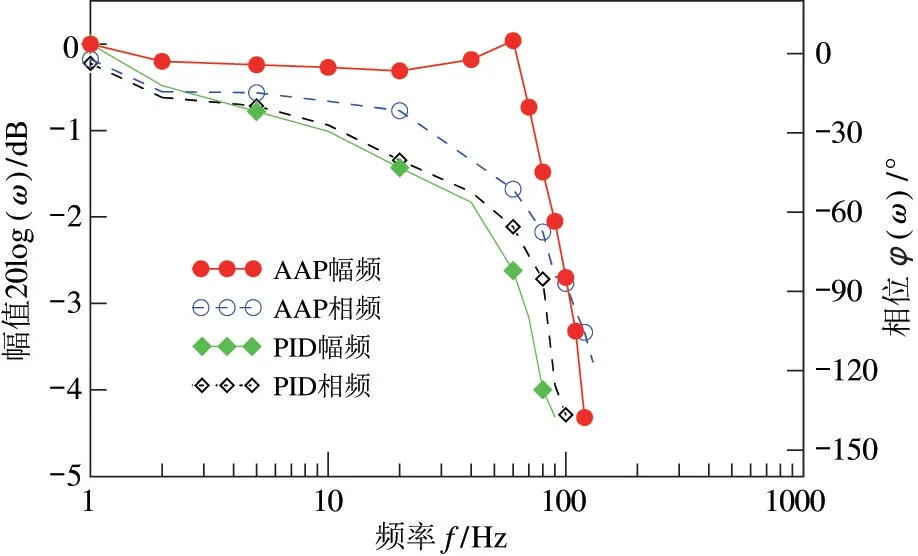
图18 2D 伺服阀的频率特性

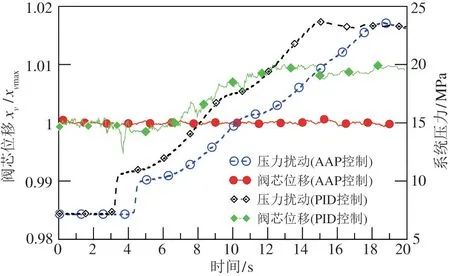
图19 阀芯位移抗系统压力扰动实验

由图17 看出,2D 伺服阀在PID 算法控制时,阶跃响应的上升时间约为8.6 ms,超调量约5%;而采用AAP 算法控制时,上升时间为6.9 ms,上升平稳无超调。由图18 看出,2D 伺服阀在PID 算法控制时,对应-3 dB、-90 °处的频宽约为65 Hz,而在AAP 算法控制时的频宽增大62%至105 Hz,虽然2D 伺服阀受限于圆孔形的高、低压小孔结构,使得初始导控流量较小,导致了频宽与测得的电-机械转换器的频宽相比大幅度下降,但是通过AAP 算法可以使其频率特性得到改善,又较大幅度提升了其动态性能。

由图19 可以看出,突然升高系统压力来对2D伺服阀的工作进行干扰时,若其在PID 控制下,阀芯位移则会出现偏移,最大偏差量是稳态值(阀芯满开口)的2.03%,明显受系统压力影响;而若让其在AAP 算法控制下,阀芯位移的最大偏差量仅为稳态值(阀芯满开口)的0.28%,可知AAP 算法对系统压力扰动具有很好的适应性,可以提升阀的鲁棒性和抗扰动能力,取得了更好的控制效果。

6 结论

本文提出了2D 伺服阀电-机械转换器参数实时优化的自抗扰同步跟踪控制算法,其能有效优化系统控制器参数。仿真和实验表明,基于该算法的电-机械转换器的动态性能和频率特性显著提升,并且在电感、摩擦力等电机内部参数变化以及外部负载干扰的情况下,比传统PID 控制算法具有更好的动态控制效果和抗扰动性能。采用AAP 算法成功解决了伺服阀分辨率和响应速度之间的矛盾,实验结果表明,基于该算法的2D 伺服阀其动态性能和频率特性得到有效提升,而且具有更好的鲁棒性、抗扰动能力,即使在系统压力变化时也具有良好的控制效果。