基于偏差的纯追踪双舵轮停车AGV 全向运动轨迹跟踪①

夏韵凯 张 征 蔡颖杰 戚鸿斌 姚富林 周圣云

(*浙江工业大学机械工程学院 杭州310023)

(**深圳怡丰机器人科技有限公司 深圳518116)

0 引言

随着国民生活水平的提高,城市的交通问题日益突出,特别是人员密集的大城市,停车难成为一种社会问题,一定程度上影响了社会的发展。近年来,自动导引车(automated guided vehicle,AGV)得到了快速发展,在自动化工厂与物流行业得到了广泛应用[1]。目前停车AGV 作为智能停车库的组成部分,越来越受到社会的广泛关注[2]。

定位、轨迹跟踪与运动控制是AGV 的核心技术[3-5]。轨迹跟踪是指移动机器人从已知的初始位姿状态开始,通过运动控制,使其能以预设的速度沿着已规划的一条几何路径行驶。常见的轨迹跟踪方法可分为预瞄式和非预瞄式[6-8]。预瞄式路径跟随通过比较机器人当前位姿与期望路径上预瞄点坐标的几何关系,对机器人转向系统进行控制从而使得AGV 能沿着规划的路径行驶。非预瞄式控制方法主要根据机器人的当前位姿状态与理论的坐标点的偏差进行控制,从而使得移动机器人沿着规划的路径行驶。常见的非预瞄式控制方法主要有比例积分微分(progortional integral derivative,PID)控制、前馈-反馈控制[9]和模型预测控制[10-12]等。PID 是工业上常用的线性控制器,控制方法简单,但其控制参数需要经过大量实验试凑法获得,而且不同机器人的PID 参数还有所区别,不适宜工业机器人的大量部署。前馈-反馈控制通过移动机器人运动参考路径曲率变化的干扰量进行运动控制量的补偿,但是该方法不适合在高速运动下的机器人,因为随着速度的提高,机器人将无法跟踪弯曲的道路[13]。纯追踪[14]是基于预瞄式系统控制,由于其稳定的性能,常用于无人驾驶汽车的轨迹控制。

目前的轨迹跟踪算法都是针对无人驾驶汽车或简单运动形式的移动机器人,无法直接应用于全向运动的双舵轮停车AGV 轨迹跟踪。因此本文基于纯追踪预瞄式系统控制思想,提出了基于偏差的纯追踪双舵轮停车AGV 全向运动轨迹跟踪。本文的主要工作内容包括以下四方面。

(1) 针对双舵轮停车AGV 建立了对应的运动模型,设计了双舵轮AGV 的全向运动控制律。

(2) 在纯追踪算法的基础上提出了基于偏差的纯追踪双舵轮AGV 全向运动轨迹跟踪算法。

(3) 通过Python 对双舵轮停车AGV 进行数学建模及仿真,成功验证了算法的可行性。

(4) 通过实车轨迹跟踪实验,验证了本文所提出控制模型与轨迹跟踪算法的有效性。

1 双舵轮停车AGV 的运动控制

1.1 双舵轮运动模型

双舵轮停车AGV 因为其驱动形式,除了普通的前进、后退、转弯、自旋运动外,还可以实现平移、横移,甚至组合运动以适应不同路径要求,环境适应性更强。

双舵轮停车的运动学模型示意图如图1 所示,X-Y为局部坐标系,两舵轮之间的轴距为2L;α、α1和α2分别为AGV 的速度方向角、舵轮1 的方向角和舵轮2 的方向角(逆时针为正);v、v1和v2分别为AGV 的速度、舵轮1 的速度和舵轮2 的速度;S1(L,0),S2(-L,0) 分别是舵轮1 与舵轮2 在局部坐标系下的坐标。需要根据舵轮的运动参数求得AGV运动参考点O的速度v与角速度ω。

因此AGV 的运动学模型可表示为

其中vx、vy为运动参考点速度v的正交分解的速度。

1.2 双舵轮停车AGV 的运动控制

常见的移动机器人控制律为[v,ω]T,即通过控制机器人的线速度与角速度,从而实现机器人的运动控制,但其并不适用于本文的双舵轮停车AGV 的运动控制。因此需要通过纯追踪算法获取能够控制双舵轮运行的控制律。本文将控制律设计为[v,α,ω]T,其中v为参考点的速度大小,α为速度方向角,ω为车体旋转角速度。通过此控制律,可以求解AGV 中各个舵轮的转角和速度大小,从而实现AGV的全向运动控制。下面是已知控制律[v,α,ω]T的情况下,求解AGV 两个舵轮的转角与速度。

从图1 可知,所示O′为刚体的旋转中心,根据刚体运动的速度投影法[15]可得:

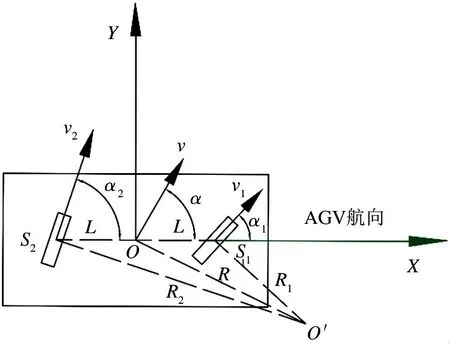
图1 双舵轮局部坐标系运动示意图

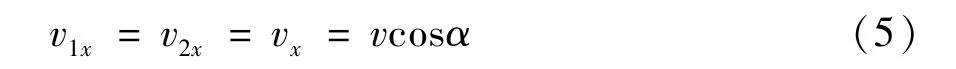
其中,vx为参考点O处速度v在局部坐标系下正交分解得到的X轴方向分速度,v1x与v2x分别为两舵轮速度v1和v2基于AGV 局部坐标系正交分解得到的X轴方向的分速度。

由式(1)与式(3)建立方程组,可得:

其中,vy为参考点O处速度v在局部坐标系下正交分解得到的Y轴方向分速度,v1y与v2y分别为两舵轮速度v1和v2基于AGV 局部坐标系正交分解得到的Y轴方向的分速度。

因此AGV 2 个舵轮的速度与角速度可表示为

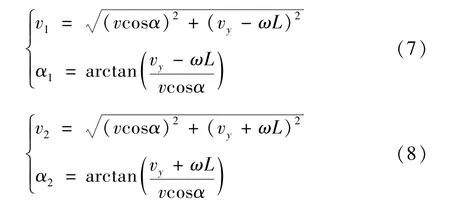
2 基于偏差的纯追踪路径跟踪

2.1 常规的纯追踪算法

纯追踪由于其简单稳定的控制算法,广泛应用于无人驾驶汽车与移动机器人中[16]。纯追踪是根据车辆与目标路径的几何关系,对车辆进行横向运动控制,从而实现轨迹跟踪。

将纯追踪算法应用于叉车AGV 的运动控制时,以叉车从动轮中心O1为切点,车辆纵向车身为切线,通过控制前轮偏角θ,使车辆可以沿着一条经过预瞄点的圆弧行驶,叉车AGV 运动过程的路径跟随过程如图2 所示。其中,O为AGV 的运动圆周中心,O1为AGV 叉车从动轮中心,O2为AGV 预瞄的参考点,wb为舵轮到参考点的距离,ld为预瞄点与当前参考点的距离,Δα为叉车与预瞄点的夹角,R1为叉车的运动半径。

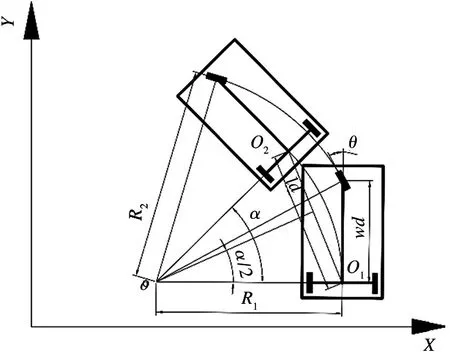
图2 叉车纯追踪算法

根据几何关系不难得到叉车纯追踪的控制量表达式:

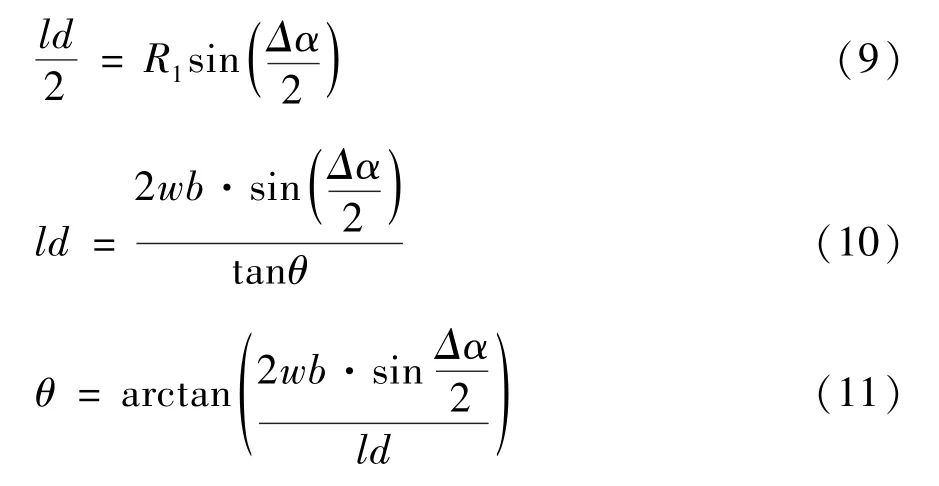
因此只需设置合理的ld值就能控制叉车运动。文献[17]已说明,预瞄参数ld与车速间存在一定数学关系:

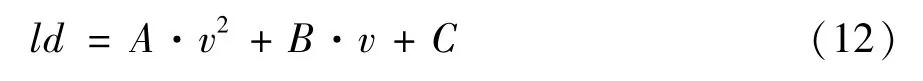
其中,v为车辆行驶速度,A、B、C均为常数项。其中A可以表示为

amax为车辆最大制动加速度,B表示车辆遇到异常情况时进行反应的车辆行驶距离,C表示为车辆最小转弯半径。

2.2 基于偏差的双舵轮停车AGV 的轨迹跟踪算法流程

叉车AGV 由于运动形式的限制,其轨迹跟踪时的航向角只能与运行的路径相切,无法实现全向运动,而双舵轮停车AGV 可以进行全向驱动。因此需要设计能够满足双舵轮停车AGV 全向运动的轨迹跟踪算法。

双舵轮AGV 全向轨迹跟踪算法的流程如图3所示,算法的具体流程描述如下。

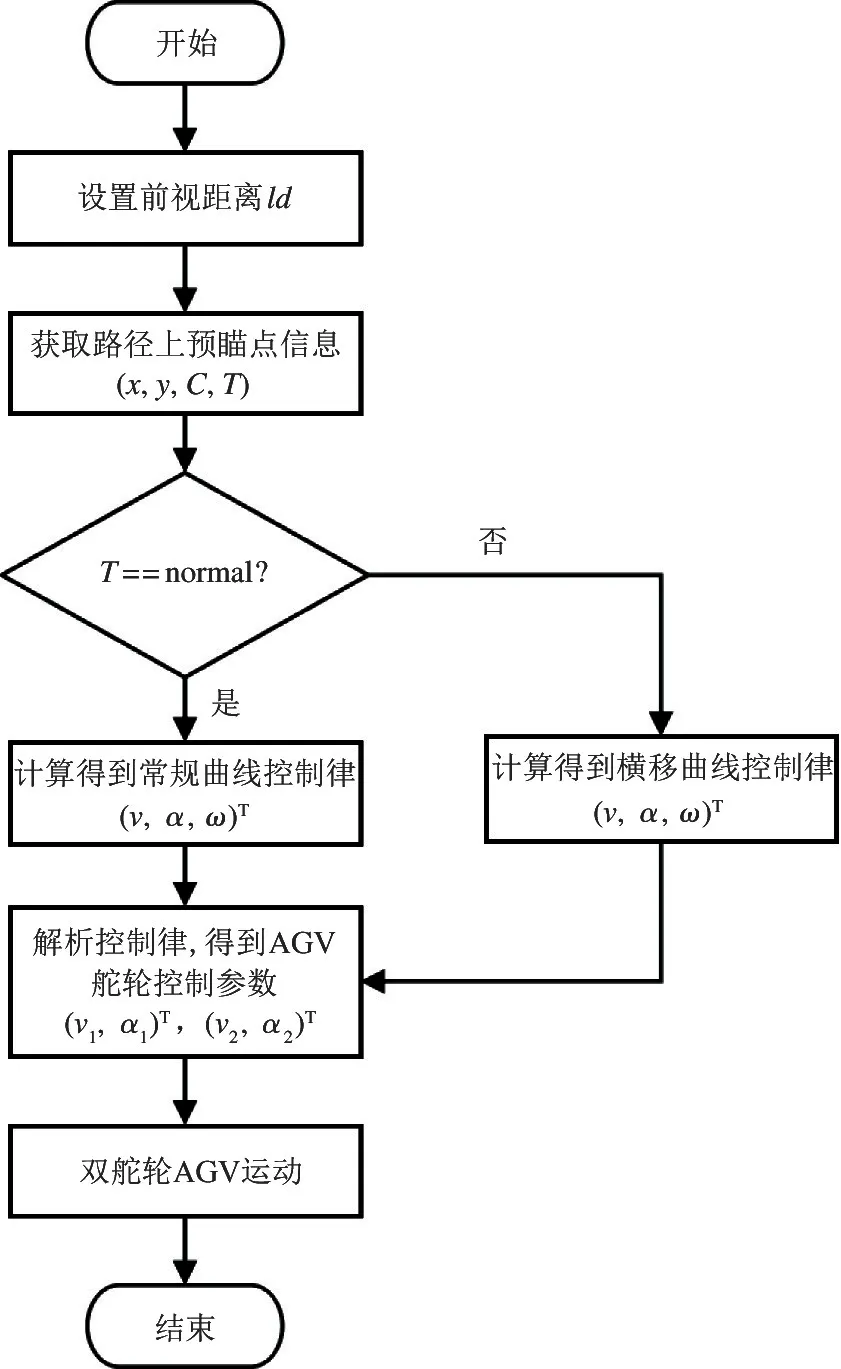
图3 AGV 全向轨迹跟踪算法流程

(1) 设置前视距离ld

图2 中叉车AGV 中的控制量是舵轮转角θ,而本文设计的双舵轮AGV 的控制量为[v,α,ω]T,因此本文对纯追踪算法进行了修改。常规曲线运动控制原理如下文的图5 所示。预瞄距离ld由式(12)确定,本文中A=0.25,B=0.1,C=350 mm。预瞄距离ld用于计算路径上的预瞄点(G点)。

(2) 获取路径上预瞄点信息

AGV 沿着设计的轨迹行走,通过前视距离与轨迹相交,得到预瞄点(G)。预瞄点的信息包括(x,y,v,C,T)。其中x与y为预瞄点位置信息;v为轨迹的设定速度;C为轨迹在预瞄点处的曲率;T为轨迹的类型。有两类轨迹,其中normal 表示常规曲线,另一类型为横移曲线。

(3) 判断路径类型并计算AGV 控制律

根据轨迹类型T获取对应的曲线类型,当T为normal 时使用下文的式(13)计算对应的控制律;当T不为normal 时,使用下文的式(14)计算对应的控制律。

(4) 解析控制律得到控制AGV 舵轮运动的参数

当得到对应的控制律后,将控制律带入式(7)与式(8)后即可得到控制AGV 舵轮运动的参数(v1,α1)T、(v2,α2)T,实现双舵轮AGV 的全向轨迹跟踪。

为了更好地分析本文提出的轨迹跟踪算法的运行效果,对实际使用的运动方式进行分析。双舵轮AGV 的主要运动形式如图4 所示,不同运动形态下两舵轮的角度与速度情况如表1 所示。本文列举了5 种运动形态,分别为自旋运动、直线前进运动、横移直线运动、常规曲线运动与横移曲线运动。表1中的变量与图1 中的变量相同。

表1 双舵轮AGV 运动分析

图4 双舵轮AGV 的运动形式

2.3 常规曲线轨迹跟踪

双舵轮AGV进行常规曲线运动时,AGV的航向角与规划路径相切,如图5 所示。通过几何关系可知常规曲线轨迹的控制律为[v,α,ω]T。其中v为轨迹中设定的AGV 运行速度,α为双舵轮AGV的参考点相对全局路径地图速度方向,ω为AGV 的运动角速度。α与ω通过式(13)可得。

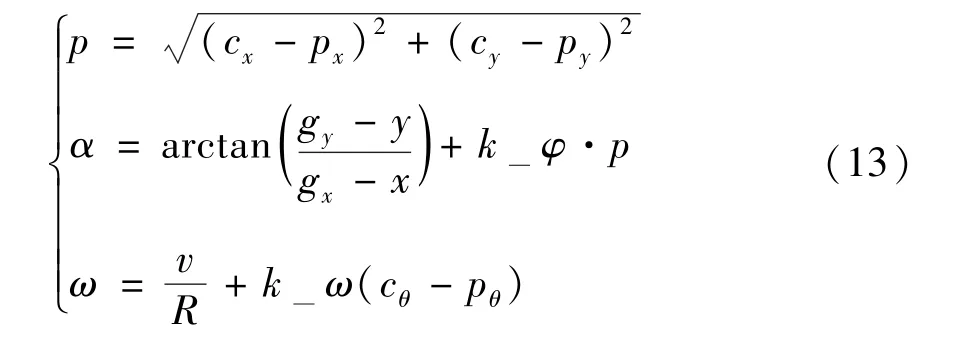
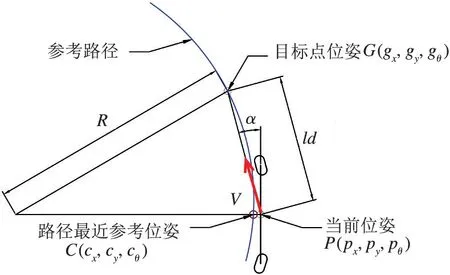
图5 常规曲线路径跟踪原理图

为了更好地控制双舵轮AGV 的运动,本文引入了偏差量控制参数k_φ与k_ω。控制的偏差为AGV 当前位姿与路径上最近位姿的位置偏差与角度偏差,通过调节k_φ与k_ω就能更好控制双舵轮AGV 的常规曲线运动。

2.4 横移曲线轨迹跟踪

双舵轮停车AGV 的优势便是可以进行横移运动,使其能在工作环境中更灵活地运动。在横移运动时,两舵轮转角α1=α2≠0,将速度v1=v2代入式(1)可得,此时车体的角速度为0,车体中心的速度等于舵轮的速度。基于偏差的双舵轮停车AGV的纯追踪控制原理如图6 所示。

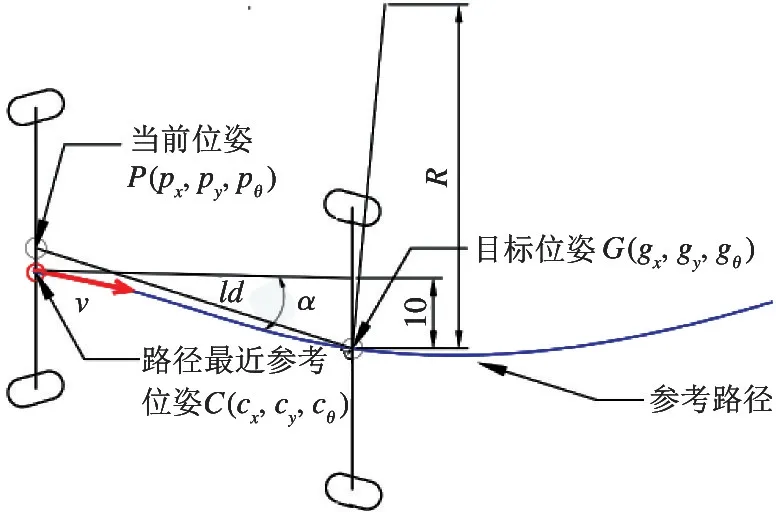
图6 横移曲线路径跟踪原理图

预瞄点确定与常规曲线运动一样,由ld控制,通过几何关系得到的横移曲线运动轨迹跟踪控制律为[v,α,ω]T。其中v为轨迹中设定的AGV 运行速度,α与ω通过式(14)可得。

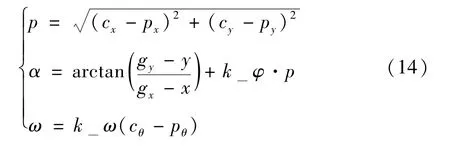
与常规曲线运动控制相同,横移曲线运动也通过调节k_φ与k_ω来更好地控制双舵轮AGV 的运动。

3 仿真与实验

为了验证双舵轮全向AGV 的路径跟踪算法的效果,对其进行了数学建模,并使用Python 实现仿真。仿真了AGV 运行过程中的大部分轨迹类型,轨迹类型包括自旋运动、直线前进轨迹、常规曲线、横移曲线,组合路径运动的轨迹如图7 所示。

仿真时,使用了PID 控制与基于偏差的纯追踪轨迹跟踪控制实现双舵轮AGV 的组合运动路径仿真。PID 控制仿真过程中AGV 舵轮转角、舵轮速度、运动参考点速度变化如图8 所示;基于偏差的纯追踪轨迹跟踪控制仿真过程中AGV 舵轮转角、舵轮速度、运动参考点速度变化如图9 所示。

图7 中的不同路径对应图9 中不同阶段。组合路径运动过程中的控制量变化符合表1 中的运动分析,即①阶段为自旋运动,两舵轮转角为α1=π/2、α2=-π/2,运动参考点的速度为v=0;②、⑥、⑩阶段为直线前进运动,两舵轮转角为α1=α2=0,运动参考点的速度为v=v1=v2;③、④阶段为常规曲线运动,两舵轮转角为α1=-α2≠0,运动参考点的速度为v=v1cosα1=v2cosα2;⑤、⑦、⑨为横移曲线运动,两舵轮转角为α1=α2≠0,运动参考点的速度为v=v1=v2。图8 的结果与图9 相近,说明两种控制均能控制双舵轮AGV 实现全向轨迹跟踪。图10 是基于偏差的纯追踪轨迹跟踪控制仿真过程中的距离偏差,表明仿真过程中的最大偏差约为45 mm,平均偏差约为10 mm。图11是PID控制仿真过程中的距离偏差,表明仿真过程中的最大偏差约为46 mm,平均偏差约为10mm。两者在仿真过程中结果相近,但是由于PID 算法需要大量调试参数,在实际工程应用中,本文提出的基于偏差的纯追踪轨迹跟踪控制具有较强的适用性。

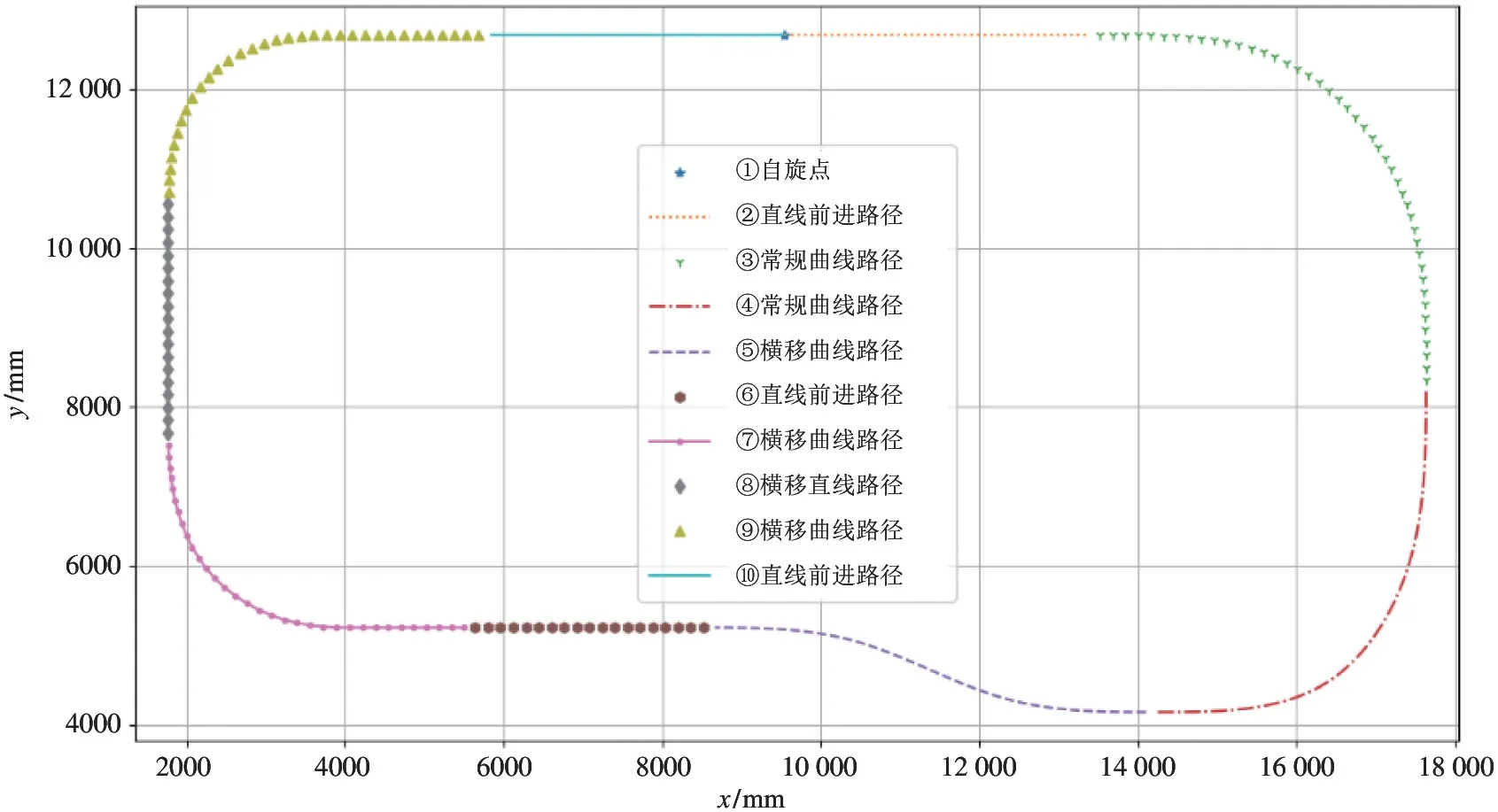
图7 AGV 组合运动路径

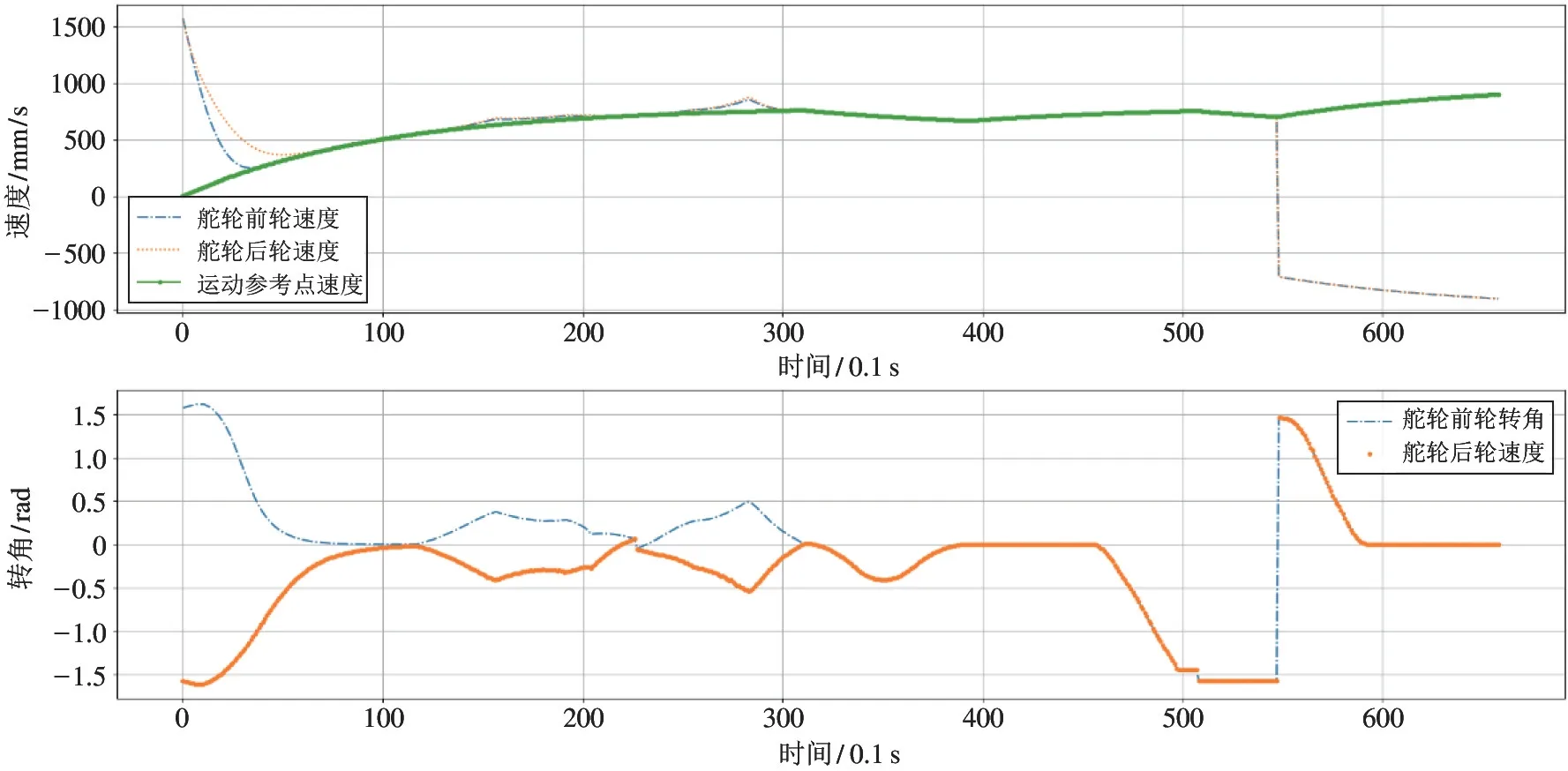
图8 PID 算法组合运动中的控制量变化

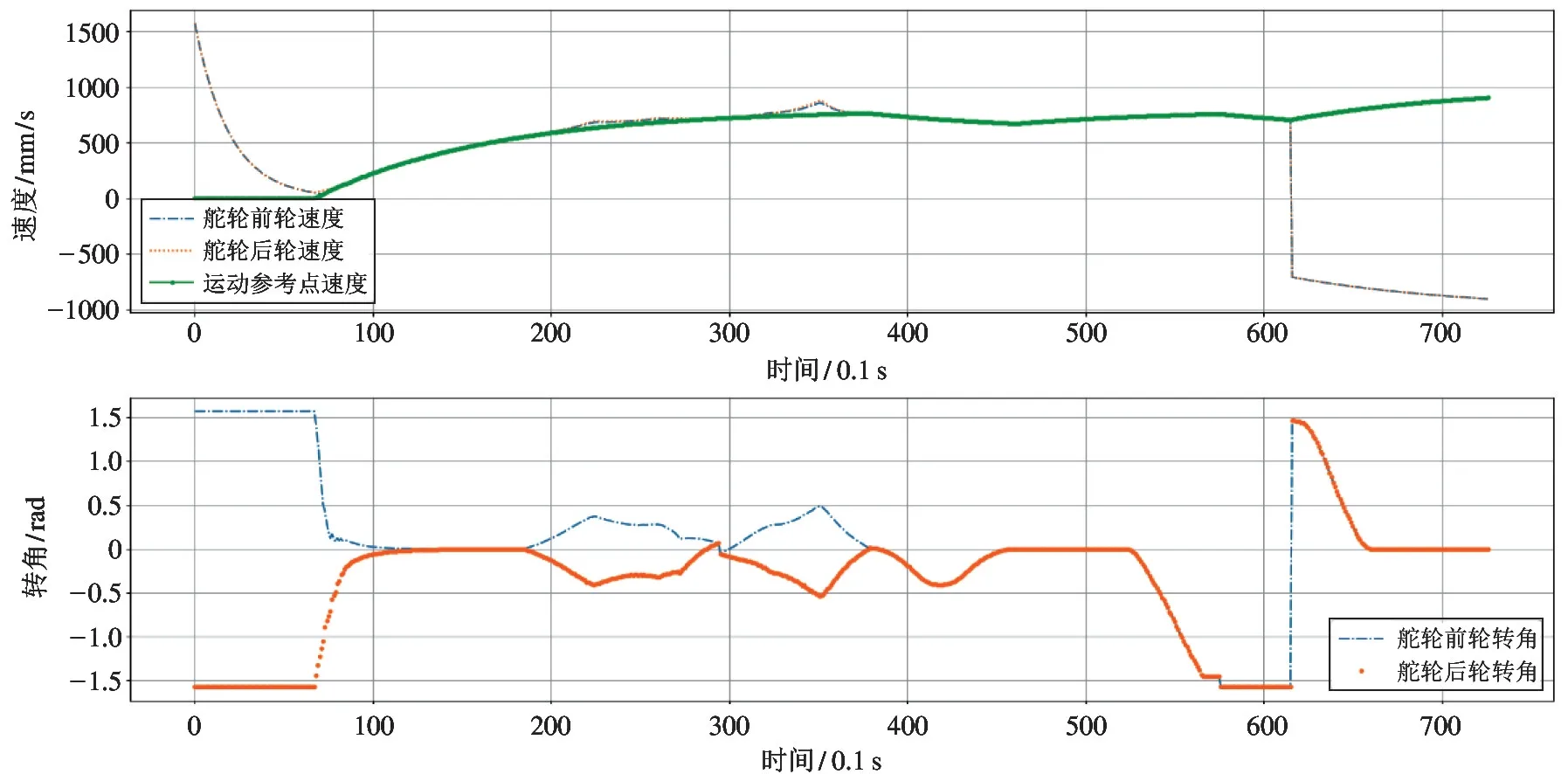
图9 基于偏差的纯追踪算法组合运动中的控制量变化

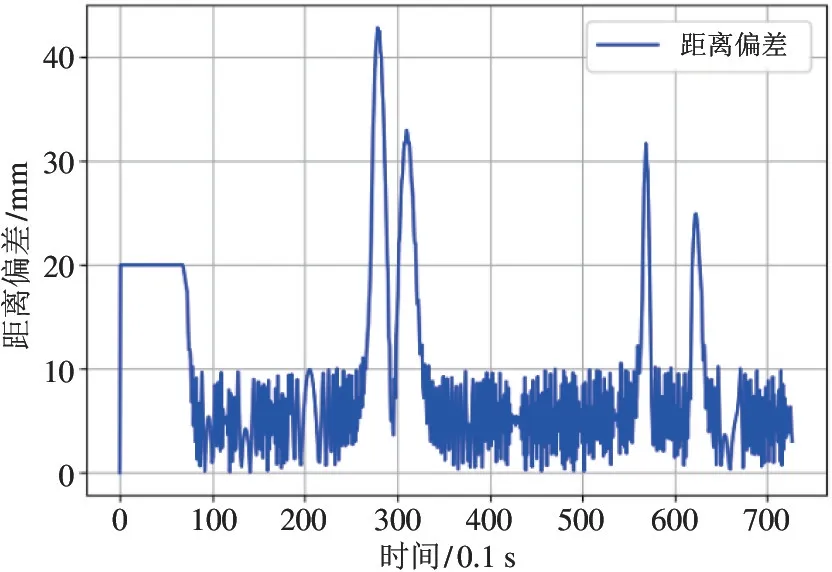
图10 基于偏差的纯追踪算法仿真距离偏差

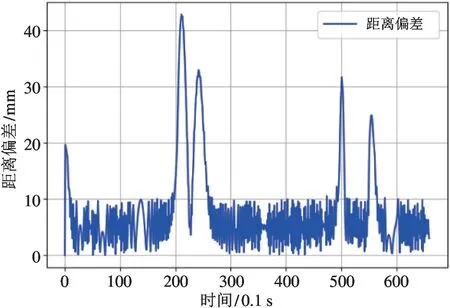
图11 基于PID 算法仿真距离偏差

为了验证本文提出的基于偏差的纯追踪轨迹跟踪控制的实际运行效果,进行了实车验证。图12 为本文研究的双舵轮停车AGV,车身尺寸为5120 mm×1580 mm,AGV 前后舵轮位于AGV 中轴线上且舵轮连线的中点与AGV 车体中心重合,舵轮之间的间距为2250 mm。AGV 采用工业计算机进行数据处理。计算机CPU 型号为Intel aton E3845,主频1.91 Hz,搭配4 GB 内存。实验中的运行路径如图13 与图14所示,分别测试了速度为500 mm/s 与800 mm/s 的轨迹跟踪情况,并且每隔0.02 s 取一次数据。图15与图16为运行过程中距离偏差曲线。

图12 双舵轮停车AGV

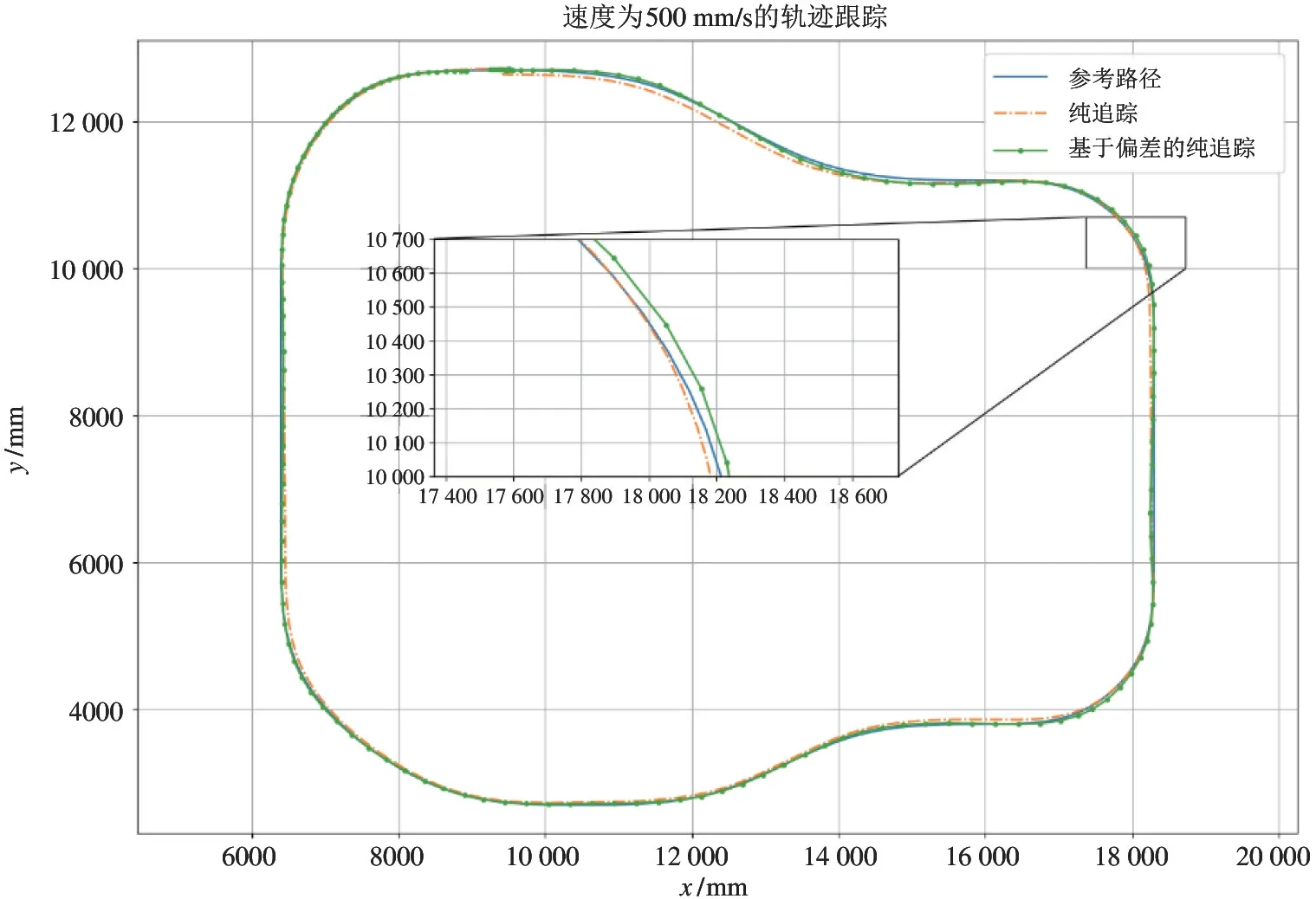
图13 速度为500 mm/s 的轨迹跟踪

图14 速度为800 mm/s 的轨迹跟踪

图15 速度为500 mm/s 的距离偏差

图16 速度为800 mm/s 的距离偏差

图15 表明,当AGV 的运行速度为500 mm/s时,基于纯追踪的双舵轮的偏差最大约为85 mm,平均偏差为30 mm 左右;基于偏差的纯追踪的最大偏差为50 mm,平均偏差为20 mm。图16 表明,当运行速度为800 mm/s 时,纯追踪的最大偏差为100 mm,平均偏差为40 mm 左右;基于偏差的纯追踪的最大偏差为85 mm,平均偏差为25 mm。

综上,本文提出的基于偏差的纯追踪双舵轮停车AGV 全向运动轨迹跟踪,能有效提高双舵轮AGV 的控制精度,实现全向轨迹跟踪。

4 结论

本文提出了一种全向双舵轮停车AGV 的运动控制方法,并使用基于偏差的纯追踪算法进行路径跟踪。仿真实验表明,该方法能够正确描述双舵轮AGV 的全向轨迹跟踪。实验验证了基于偏差的纯追踪算法相较简单的纯追踪算法其控制精度有较大提升,该方法能有效控制双舵轮AGV 的全向运动控制。