考虑行波效应的大跨度悬索桥地震响应分析
张世蒙 王贵春岳凯乐
(郑州大学土木工程学院,郑州 450001)
0 引 言
悬索桥是目前世界上广泛采用的大跨径桥梁,具有超强的跨越能力。悬索桥由于自身特性以及昂贵的维护费用,成为健康检测以及抗风抗震研究的主要对象之一[1-2]。目前对桥梁进行地震分析时,一致激励是常用的分析方法,但由于悬索桥跨度一般较大,还需要考虑地震动的空间效应[3]。大跨度悬索桥为长周期结构,当遇到大震或地震低频成分丰富时,易发生共振导致桥梁破坏。所以对大跨度结构进行抗震研究时,长周期地震作用下行波效应的影响分析不容忽视[4-5]。
国内外学者对该课题进行了一系列的相关研究。Shehata E.Abdel Raheem等[6]以某一斜拉桥为例,研究了地震动空间效应对斜拉桥地震响应的影响,证明了考虑行波效应的重要性。焦常科等[7]以泰州长江大桥为例进行行波效应分析发现:低视波速对结构响应的影响具有一定的震荡性,并随着视波速的增大趋于稳定。闫聚考等[8]以泰州长江大桥为例,建立1/40缩尺模型,进行全振动台试验,研究在三种不同纵向约束条件下行波效应对结构响应的影响,得出结论:行波效应对结构影响与结构自身特性和地震动特性密切相关,但文中所选视波速仅为低值,并没有选高视波速进行分析,也没有与一致激励结果进行对比。丁幼亮等[9]以泰州大桥为例,选取了7条近断层地震波、7条普通地震波进行多塔悬索桥地震响应对比分析,研究发现:在两种不同地震作用下,地震响应分布规律基本一致,受地震波自身特性和场地土的影响,峰值有所差别。文中虽对地震波进行了讨论,但未分析行波效应的影响。目前,做悬索桥行波效应研究时,大多数仅考虑了安评报告提供的加速度时程或一些常见的普通地震波。在近些年发生的地震中,长周期地震动对高层建筑以及大跨度桥梁造成的破坏更大,因此需要对其进一步研究。
以润扬长江大桥为研究对象,采用ANSYS有限元分析软件,建立不考虑土-桩-结构相互作用的悬索桥有限元模型。选取100~8000m/s范围内9组不同的视波速,采用时程分析方法,分析行波效应对大跨度悬索桥地震响应的影响,并探讨了在普通地震动、远场地震动及近场地震动作用下行波效应对大跨度悬索桥地震响应的影响。
1 工程概况
润扬大桥为单跨双铰简支悬索桥,中跨跨径为1 490 m,边跨跨径为470 m,在设计成桥状态下,中跨主缆理论垂度为149.605 m,垂跨比约为1∶10,桥型图如图1所示。主梁为扁平流线型钢箱梁,正交异性板桥面,梁高3 m,全宽38.7 m。主缆共两根,中心距为34.3 m,吊索间距为16.1 m,其中近塔吊索距塔中心线20.5 m,为适度增强结构纵向刚度,避免跨中短吊杆的弯折现象,在跨中设置刚性中央扣。索塔是由两个塔柱、三道横梁组成的门式框架结构,塔柱为钢筋混凝土空心箱形结构,塔高210 m。

图1 成桥状态桥型总体布置图Fig.1 General layout plan of bridge type
2 有限元模型及动力特性
图2为润扬大桥的“脊骨梁式”空间有限元模型。桥面系、中央扣和主塔均采用空间梁单元模拟,加劲梁按照吊杆的吊点进行离散。加劲梁和吊杆采用刚臂连接。主缆和吊杆采用空间线性杆单元进行模拟,主缆也按照吊杆的吊点进行离散,单元受力模式为只受拉不受压。下文简称扬州侧主塔为北塔,镇江侧主塔为南塔。桥梁构件截面特征和材料参数参照文献[2]所设。

图2 悬索桥有限元模型Fig.2 Finite element model of suspension bridge
所建模型对边界条件的处理如下:在主梁梁端处耦合主梁和主塔的横桥向、竖桥向以及绕顺桥向的转动自由度;主缆和主塔顶部自由度全部耦合,不发生相对位移;边缆底部以及主塔底部固结,不考虑桩土结构相互作用。润扬悬索桥有限元建模时采用的约束和边界情况如表1所示。
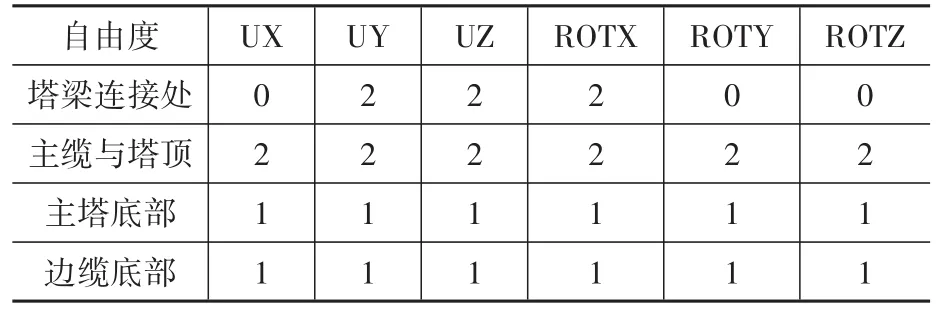
表1 模型约束及边界条件Table 1 Model constraints and boundary conditions
模态分析是进行抗震分析的基础。采用Block Lanczos法对该大跨度悬索桥进行模态分析,计算模态数为200阶,表2仅展示前20阶自振特性:该桥基频为0.049 857 Hz,基本周期较长,该桥的纵飘振型并没有在前20阶中出现,这主要是受刚性中央扣的影响。前20阶主要以主缆和主梁的振动为主,符合大跨度悬索桥这种柔性结构体系动力特征的一般规律。
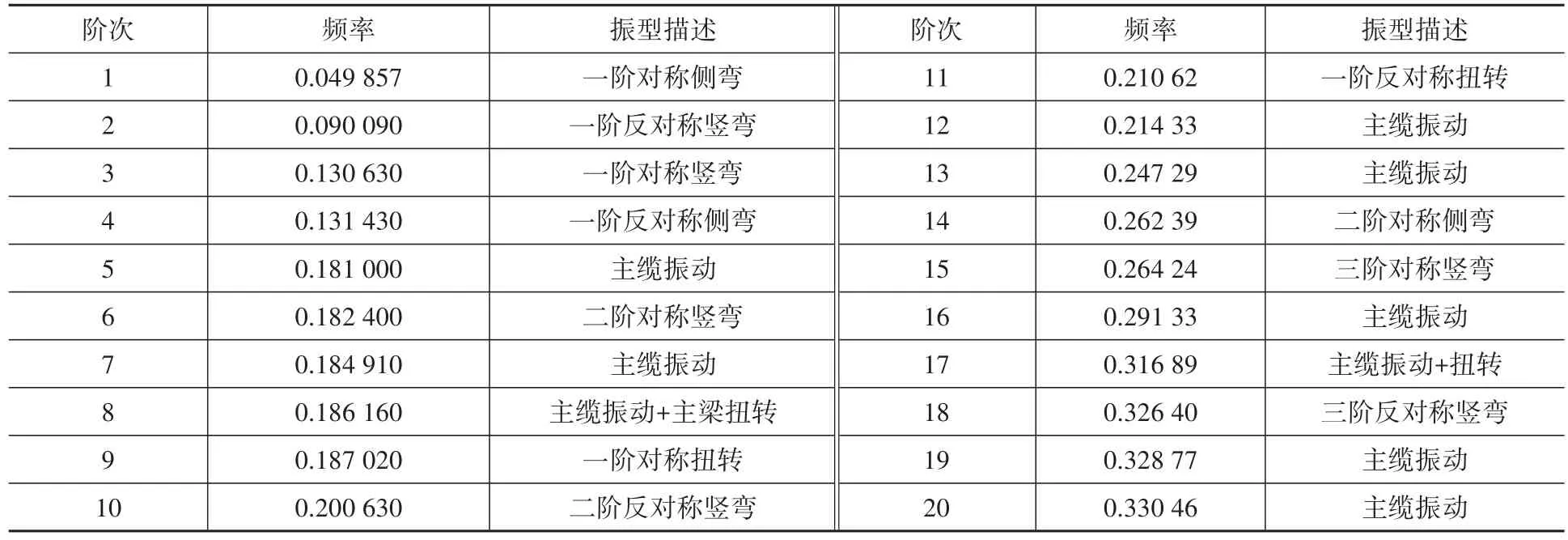
表2 动力特性分析Table 2 Dynamic analysis of the suspension bridge characteristics
3 地震波
由于地震动本身有很强的随机性,不同的地震波有不同的震级、频率、加速度峰值以及持时等[10]。根据《公路桥梁抗震设计细则》[11](JTG/T B02-01—2008)规定,本文采用3条地震波进行对比分析。其中包括El Centro波南北向,另外2条为远场地震波Chi-Chi-Taiwan CHY101(简称CHY101)和近场脉冲型地震波Chi-Chi-Taiwan TCU102(简称TCU102)。远场地震动和近场地震动均属于长周期地震动,但两者在孕育机制、频谱特性等诸多方面都各不相同[12],因此各选一条典型地震波进行计算。图3分别是3条地震波的加速度时程曲线。为防止在进行行波效应分析时位移时程发生纵飘现象,采用SeismoSignal软件对地震波进行基线调整[4,13],保证地震波速度和位移时程曲线在地震波结束时回到零轴线。图4以El Centro波为例给出SeismoSignal软件对地震波进行基线调整前后地震波速度和位移时程曲线的差异。

图3 地震波加速度时程曲线Fig.3 Time-history curves of seismic wave acceleration
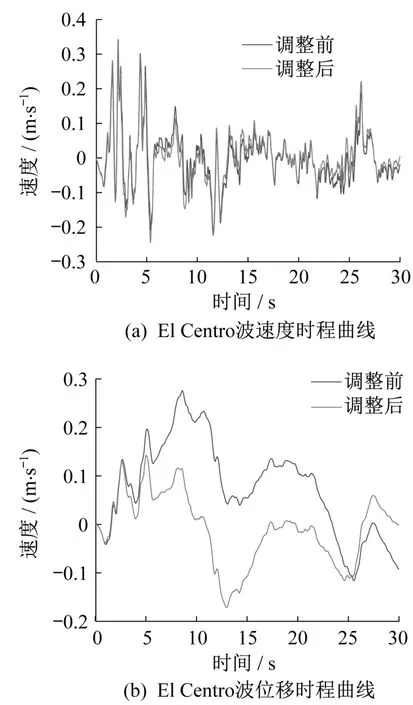
图4 El Centro波经调整后时程曲线差异对比Fig.4 Comparative differences of time-history curves of El Centro seismic wave
4 行波效应分析
采用大质量法对所建模型进行行波效应分析,地震波加速度峰值为0.3g。不考虑土-桩-结构相互作用,阻尼比取0.01。所设大质量为模型总质量的106倍,以两边缆底部及两主塔底部为地震波输入点。做行波效应分析时,视波速是悬索桥地震响应的关键影响因素,本文所选视波速为100 m/s、200 m/s、500 m/s、1 000 m/s、1 500 m/s、2 000 m/s、4 000 m/s、6 000 m/s和 8 000 m/s,共 9组。地震波按照到达时间差输入,如表3所列。图5给出所采用的视波速与地震波持时之间的关系。
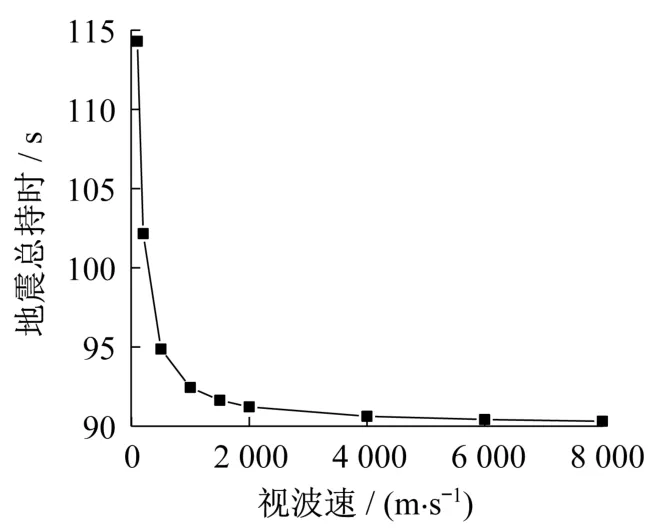
图5 视波速对地震总持时的影响Fig.5 Effect of apparent wave velocity on total seismic duration
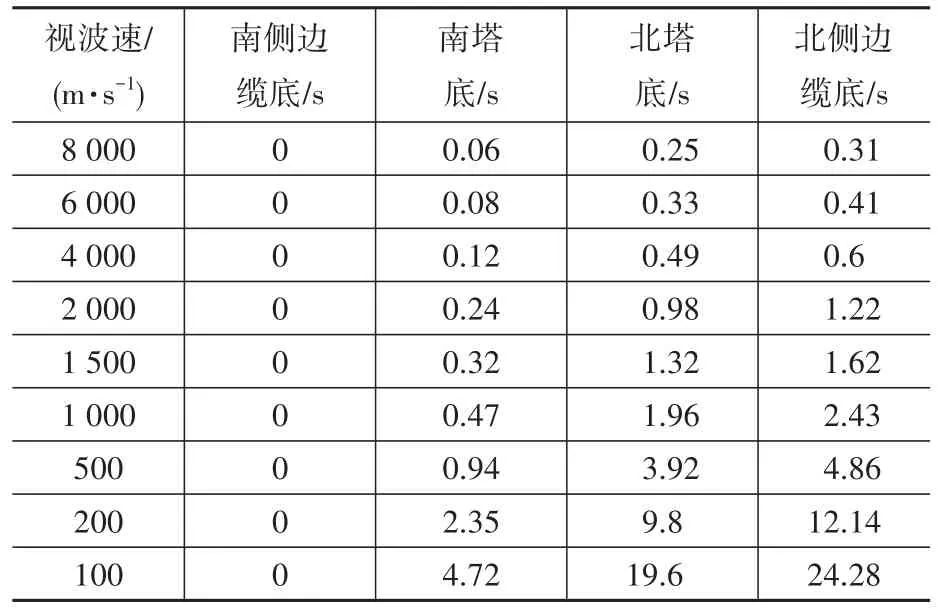
表3 行波效应分析时不同视波速下对应的时间差Table 3 Time interval at different apparent wave velocity when considering travelling wave effects
限于篇幅,图6作仅给出在TCU102地震波作用下三组不同视波速的塔梁相对位移时程曲线。可以看出,视波速的不同会影响地震响应的峰值以及地震总持时,视波速为100 m/s时,地震总持时明显增加。以塔梁相对位移、塔顶顺桥向位移、塔底横向弯矩、塔底顺桥向剪力为主要分析结果展开讨论。文中所述均为南塔以及主梁南侧的地震响应结果。
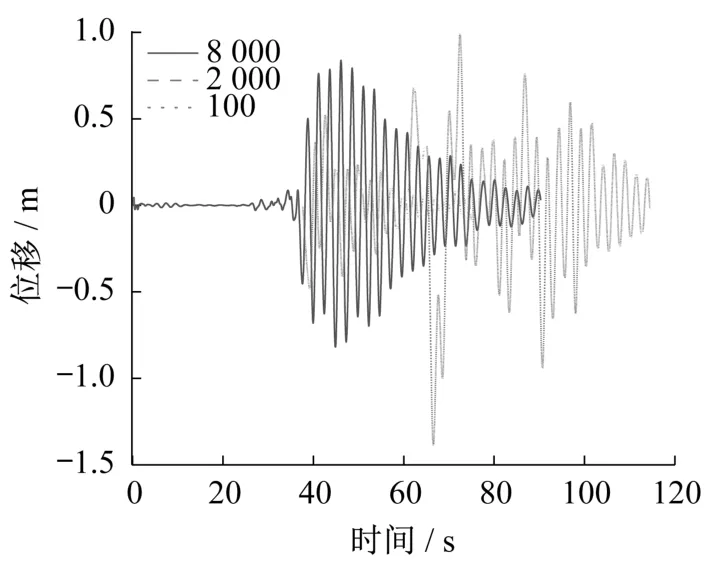
图6 TCU102波输入下塔梁相对位移时程曲线Fig.6 Time history curves of relative displacement between tower and beams input TCU102
图7—图10给出了在三种不同地震波作用下视波速为8 000 m/s时的地震响应时程曲线。可以看出,近场地震TCU102波产生的地震响应最大,远场地震CHY101波的次之,El Centro波作用下的对应值最小。
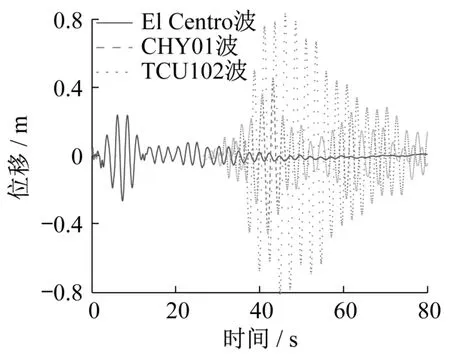
图7 塔梁相对位移曲线Fig.7 Time history curves of relative displacement between tower and beams
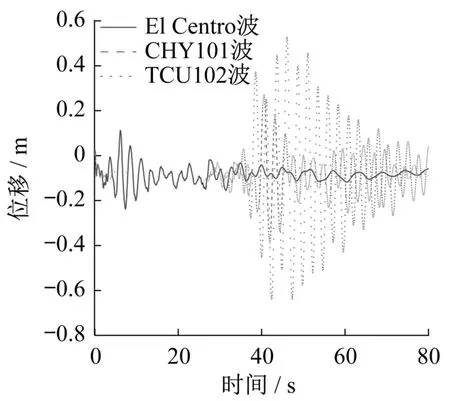
图8 塔顶位移时程曲线Fig.8 Time history curves of displacement at tower top
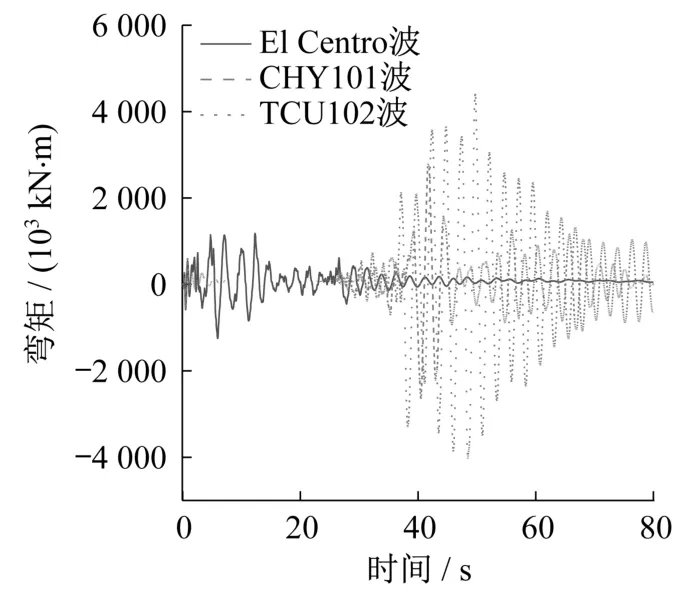
图9 塔底弯矩时程曲线Fig.9 Time history curves of bending moment at tower bottom
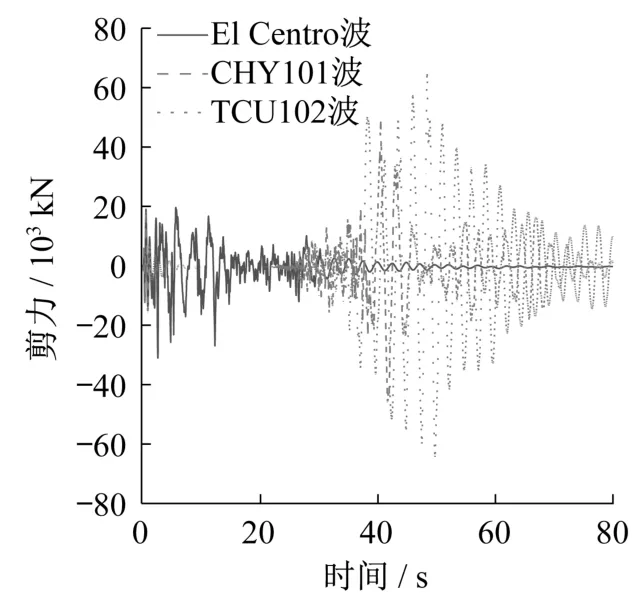
图10 塔底剪力时程曲线Fig.10 Time history curves of shear force at tower bottom
在图7中,近场脉冲型TCU102波作用下的塔梁相对位移峰值为0.838 1 m,是El Centro波输入下对应值的3.14倍;远场CHY101波作用时的对应值为0.463 5 m,是El Centro波输入下对应值的1.73倍。
由图8可以看出,近场脉冲型TCU102波作用下塔顶位移峰值为0.641 6 m,远场CHY101波作用时的对应值为0.390 2 m,分别是El Centro波输入下对应值的2.7倍和1.64倍。
图9显示,El Centro波输入下产生的塔底弯矩峰值为1 248 MN·m,比TCU102波作用下的对应值小28.2%;图10中塔底剪力峰值,TCU102波作用时较El Centro波作用时增加了1.62倍。产生上述现象的原因是,大跨度悬索桥为飘浮的柔性结构,自身阻尼较小,基频较小,因此结构响应对地震波中的低频成分更加敏感。
从图11给出的功率谱密度曲线可以看出,El Centro波的卓越频率为1.464 8,远场地震波CHY101的卓越频率为0.336 7,近场脉冲型地震波TCU102的卓越频率为0.408 9。对于大跨度悬索桥这种长周期结构,地震波卓越频率与结构频率越接近,引起的地震响应越大,当地震波的卓越频率等于结构频率时,结构的响应最大[14]。近场脉冲型TCU102波的低频成分更加丰富,且卓越频率更接近于桥梁结构基频,因此产生的结构地震响应更大。
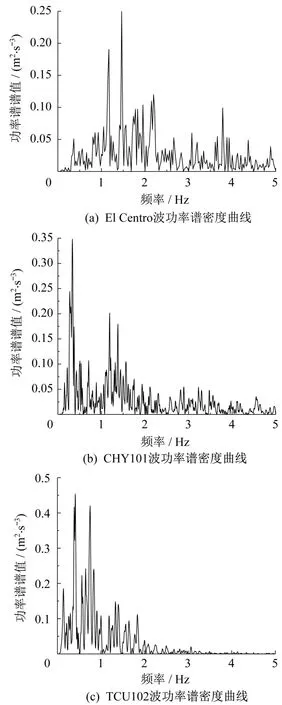
图11 地震波功率谱密度曲线Fig.11 Wave power spectral density curve
图12给出了三种地震波沿纵向输入下,塔梁相对位移峰值随视波速变化的关系。可以看出,在近场脉冲型TCU102波作用下,无论考虑行波效应还是进行一致激励,所得塔梁相对位移峰值都是最大的,说明大跨度悬索桥对低频成分丰富的地震波更加敏感。当视波速小于2 000 m/s时,三种地震波作用下塔梁相对位移峰值总体上呈现下降的趋势;视波速大于2 000 m/s时,峰值逐渐增加并接近一致激励的对应值。考虑行波效应时,TCU102波、CHY101波和El Centro波输入下,塔梁相对位移峰值分别达到一致激励对应值的1.59倍、1.39倍和1.27倍。
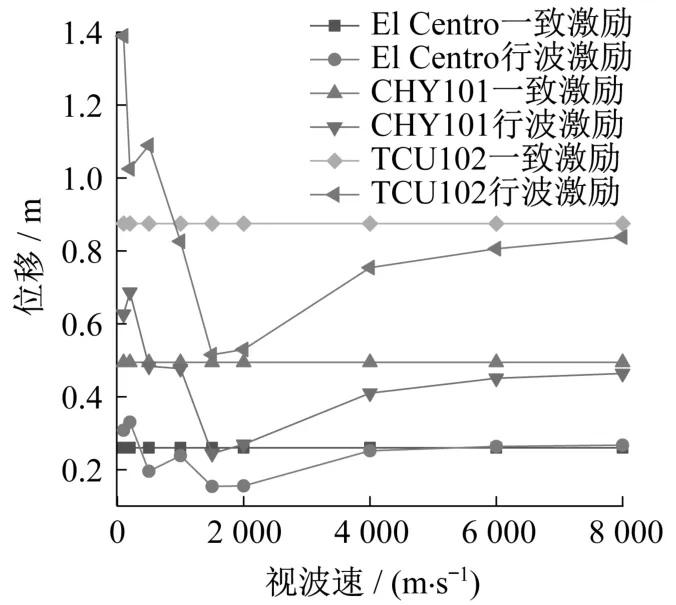
图12 视波速对塔梁相对位移峰值的影响Fig.12 Effect of apparent wave velocity on the peak value of relative displacement between tower and beams
图13给出了塔顶位移峰值随视波速变化的趋势。对比三种地震波所得结果可以看出,TCU102波作用下,塔顶位移峰值更大。视波速小于2 000 m/s时,响应值有所波动,在2 000 m/s之后,塔顶位移峰值呈现增加的趋势并逐渐接近一致激励的对应值。
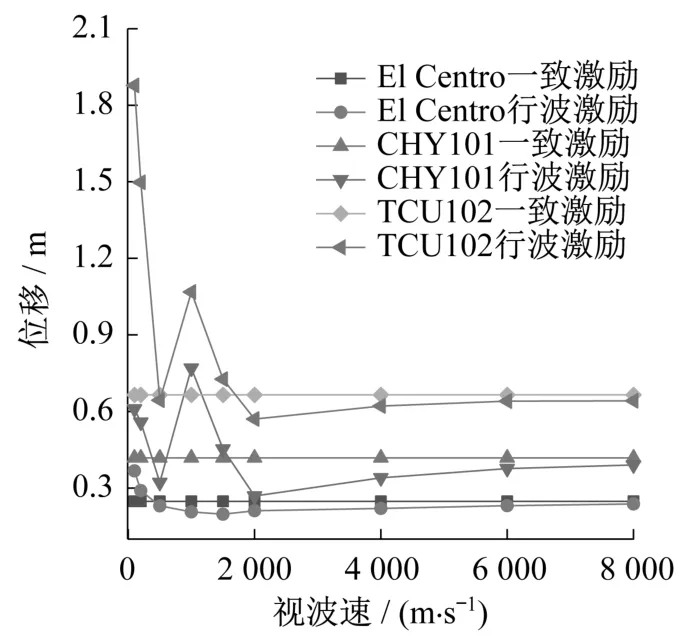
图13 视波速对塔顶位移峰值的影响Fig.13 Effect of apparent wave velocity on peak displacement at tower top
在TCU102波输入下,当视波速为100 m/s时,塔顶位移峰值达到最大,为一致激励对应值的2.83倍。在CHY101波作用下,当视波速为1 000 m/s时,塔顶位移峰值最大,为0.769 3 m,是一致激励对应值的1.84倍。在El Centro波作用下,当视波速为100 m/s时,塔顶位移峰值达到最大值0.367 1 m,是一致激励对应值的1.48倍左右。
图14为塔底弯矩峰值与视波速的变化关系图。从图中得出,近场脉冲型地震波TCU102作用时地震响应更加显著。在视波速小于2 000 m/s时,塔底弯矩峰值随视波速的变化波动较大,视波速大于2 000 m/s之后,可以明显看出塔底弯矩峰值越来越接近一致激励的对应值。
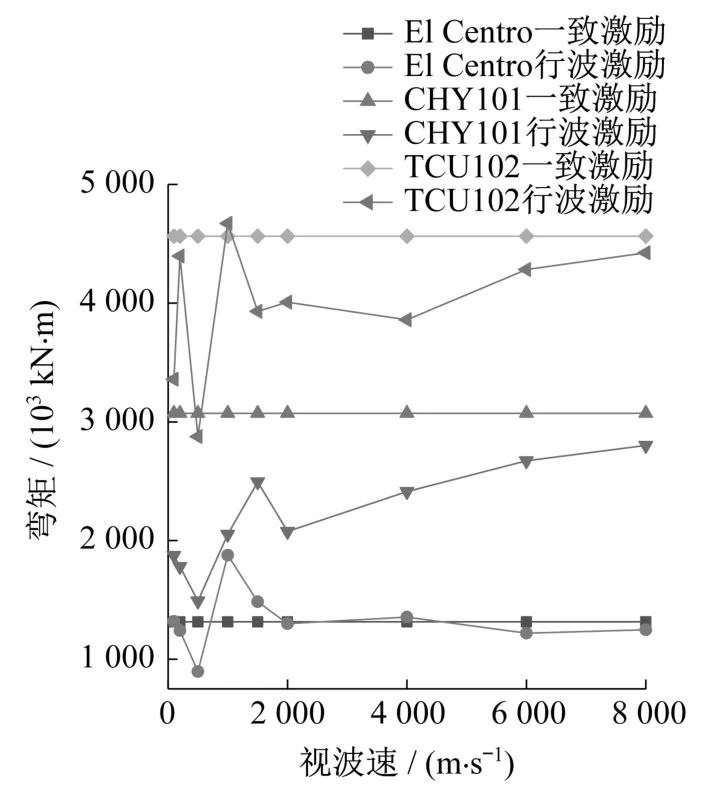
图14 视波速对塔底弯矩峰值的影响Fig.14 Effect of apparent wave velocity on peak moment at tower bottom
在TCU102波输入下,仅当视波速为1 000 m/s时,塔底弯矩大于一致激励的对应值,为4 672 MN·m,其余视波速对应的塔底弯矩峰值均小于一致激励的对应值,当视波速为500 m/s时达到最小值,为2 875 MN·m。在CHY101波作用下,考虑视波速时所得塔底弯矩峰值均小于一致激励的对应值,当视波速为500 m/s时,塔底弯矩峰值达到最小值1 490 MN·m。在El Centro波作用下,在所选视波速范围内,塔底弯矩峰值呈现先减小后增大再减小的趋势,当视波速为500 m/s时,其值最小,为896 MN·m;当视波速为1 000 m/s时,其值最大,是一致激励对应值的1.43倍。从上述分析可以看出,当视波速为500 m/s时,塔底弯矩值均最小。
图15给出塔底剪力峰值随视波速变化的关系。从图中可以看出,在两条长周期地震波作用时,产生的塔底剪力峰值均小于一致激励的对应值,而在El Centro波作用下,考虑行波效应时所得塔底剪力峰值基本均大于一致激励的对应值。在TCU102波作用下,当视波速为100 m/s时,塔底剪力峰值最小,为48 MN;而一致激励的对应值为73 MN。在CHY101波输入时,当视波速取100 m/s时,塔底剪力峰值达到最小,为33 MN,而一致激励的对应值为52 MN。在El Centro波输入下,当视波速为1 000 m/s时,塔底剪力峰值最大为40 MN,是一致激励对应值的1.62倍。
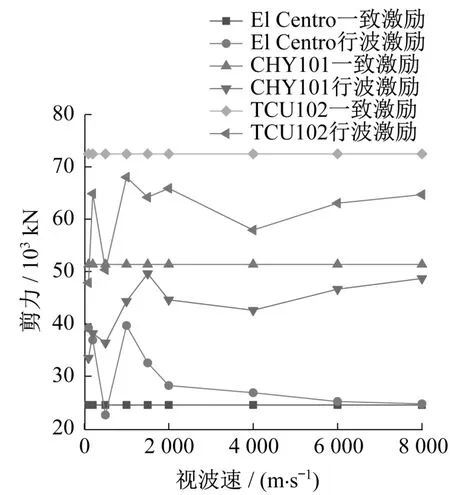
图15 视波速对塔底剪力峰值的影响Fig.15 Effect of apparent wave velocity on peak shear force at tower bottom
在图16中,以东南大学王春峰[15]所做泰州大桥为例,与本文润扬大桥地震行波效应分析对比,均采用El Centro波沿纵桥向输入。可以看出:对于大跨度悬索桥,考虑行波效应时,地震响应峰值在低视波速区间内波动较大,随着视波速增大,峰值逐渐接近一致激励对应值,验证了行波效应分析的正确性。低视波速区间内波动较大的现象说明抗震分析时考虑行波效应的必要性,并且仅选一种视波速进行分析是不科学的,需要选择多组合适的视波速进行分析,使结果具有普遍性。从图中可以看出,不同的桥梁得到的峰值曲线图不同,说明行波效应的影响与桥梁自身特性也有关系。
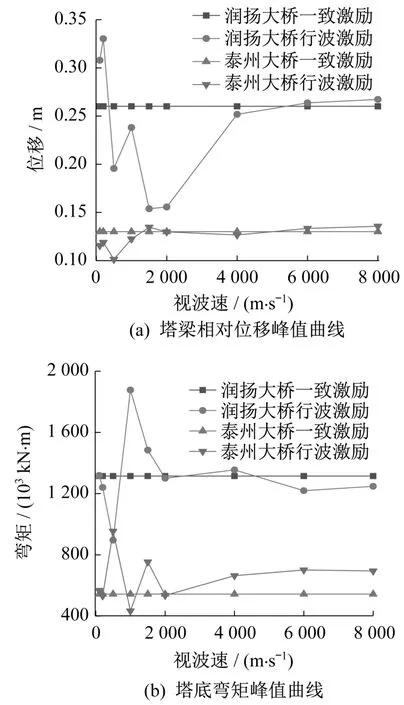
图16 不同悬索桥地震响应对比图Fig.16 Comparison of seismic response of different suspension bridges
5 结 论
(1)采用近场脉冲型地震波Chi-Chi-Taiwan TCU102得到的悬索桥地震响应最为显著,其次为远场地震波Chi-Chi-Taiwan CHY101作用下的地震响应,El Centro波作用下的对应值最小。近场脉冲型TCU102波的低频成分更加丰富,且卓越频率更接近结构基频,地震响应更大。
(2)对比一致激励分析,行波效应对悬索桥的地震响应影响较大。在低视波速区间内,塔梁相对位移最高达到一致激励对应值的1.59倍,塔顶位移最高为一致激励对应值得2.83倍。但在高视波速区间内,视波速的影响明显减低,位移峰值小于一致激励的对应值,并开始逐步接近一致激励的位移峰值,验证了行波效应计算结果的正确性。
(3)输入不同地震波时,行波效应的影响也不相同。塔底内力峰值,随视波速的增大逐渐接近一致激励对应值;但在低视波速区间内,内力峰值波动较大。
(4)对于类似大跨度悬索桥这种长周期柔性结构的设计,应充分考虑行波效应的影响。在抗震计算时,也要充分考虑低频成分较为丰富的一类地震波对桥梁地震响应的影响。行波效应对结构地震响应的影响与结构自身特性及地震波特性均有关系,所以在分析时,要正确建模、合理选择地震波。

