基于BP神经网络的航空发动机气路故障诊断研究

石向阳

(滨州学院 飞行学院，山东 滨州 256603)

0 引言

由于航空发动机在飞机系统中的特殊重要性，维修过程中不允许出现差错，一旦出现故障就可能导致飞机出现空中停车[1]等危险事故，严重影响飞机的正常使用，甚至酿成航空事故，从而造成大的经济损失。因此，航空发动机的故障诊断和状态监控格外重要。

近年来，有关神经网络的算法研究成为人工智能领域热点问题。神经元模型来源于生物的大脑，大脑里有非常多的脑细胞，每一个脑细胞可以看作是一个神经元，神经元之间相互连接构成一个复杂的神经网络[2]。神经网络包含有多种模型，例如基于梯度算法的BP神经网络、Elman神经网络和RBF径向基神经网络等[3]，每种算法的特点不同，适用范围也有所区别，其中，BP神经网络应用范围最广。BP神经网络属于一种依据误差逆传播算法训练的特殊多层前馈网络，该方法能够解决一些复杂问题，且能够对此展开推测、联想与记忆等系列环节[4]，使得故障诊断率得以提高，所以BP神经网络很适合应用于现代大型仪器设备，例如汽车、飞机等的故障诊断。

国内外许多学者针对BP神经网络应用展开了研究，例如FENG提出了基于BP神经网络的航空活塞发动机机油系统故障诊断[5]，乔文生等提出了将BP神经网络应用于立磨齿轮箱专家诊断系统[6]，牛华提出了将BP神经网络应用于汽车发动机故障诊断[7],朱涛提出将ABC-BP神经网络应用于航空发动机故障诊断[8]，均为该领域研究奠定了一定基础。本文采用目前应用最广泛的BP神经网络算法，针对PW4000航空发动机气路故障进行诊断研究。

1 BP神经网络算法

BP神经网络可以包含大量的输入与输出关系，它的网络结构包含三层：输入层、隐含层和输出层[3]。在隐含层的传输输入后，如果样本输出的期望值与实际输出值相差比较大，则转向反向传播，系统调整各层的连接权值以减少误差，直到满足精度要求。一个典型的BP神经网络结构如图1所示[7]。

图1 BP神经网络图

2 故障数据的处理

2.1 故障数据收集

因为航空发动机的数据很多，根据相关的文献资料，确定出几个可以反映出发动机故障类型的数据。本文所选取的数据来自某航空公司PW4000发动机的巡航状态时的历史监测数据，一共讨论了4种气路故障，分别是：发动机高压压气机故障、低压压气机故障、高压涡轮故障和低压涡轮故障[9]。为简便计算，数据的采集只有4种，分别是发动机排气温度TEGT(K)、燃油流量mf(kg/s)、高压转子转速N2(rpm)和低压转子转速N1(rpm)。实验中，每种故障各收集了50组数据，故障总数为200组。将40组数据用做测试，10组数据用来验证。

2.2 线性函数归一化处理数据

线性函数归一化在处理数据中很常见，通过线性函数归一化可以把数据放置于单位为一的区间内，可以更快更方便的计算数据。公式如下：

x=(xi-xmin)/(xmax-xmin),

式中，x表示线性函数归一化处理后得到的数值，xi表示每个发动机性能参数第i个样本值，xmin表示数据样本中的最小值，xmax表示数据样本中的最大值。

因为所处理数据太多，本文仅选择部分典型数值，以作为线性函数归一化数据，见表1。

表1 部分线性函数归一化数据

2.3 确定故障优先级

神经网络一般会有很多个输入变量，每个变量的特征都很难预先判定。其中会有很多无关的输入变量，这些变量会增加模型运算的复杂程度，使模型的误差变大。所以，对输入变量进一步筛选后再入模型成为很重要的一步。本文采用的是平均影响值算法，它用来表示输入对输出影响的大小，运算结果的符号代表是正相关还是负相关，绝对值的大小表示产生影响的大小。将训练的样本同时增加10%，构成一组新的数据，把这组数据作为模型的输入向量。在一般的情况下，TEGT、mf、N1、N2这4个性能参数为主要的监测对象。运算的公式如下：

Miv=|Y-Yout|。

式中，Yout表示输出向量，Y表示输入向量增加10%后的结果，Miv值表示无量纲。

经过计算，平均影响值如表2所示。

表2 故障平均影响值表

由表2可以得出，N2的总和最小，说明N2对网络的影响程度最小，当要简化时，可以首先考虑减少N2的数据。

3 BP神经网络模型在航空发动机故障诊断中的应用

3.1 故障模型的建立

将上述确定的4种故障类型，分别用Y1～Y4表示，数字1表示该部件发生了故障，数字0表示该部件完好。故障模式Y=(Y1,Y2,Y3,Y4)为神经网络的输出量，并将它们的输出量用阿拉伯数字1、2、3、4表示，得表3故障模式。综上，本文确定的故障模式为Y=(TEGT,mf,N1,N2)。

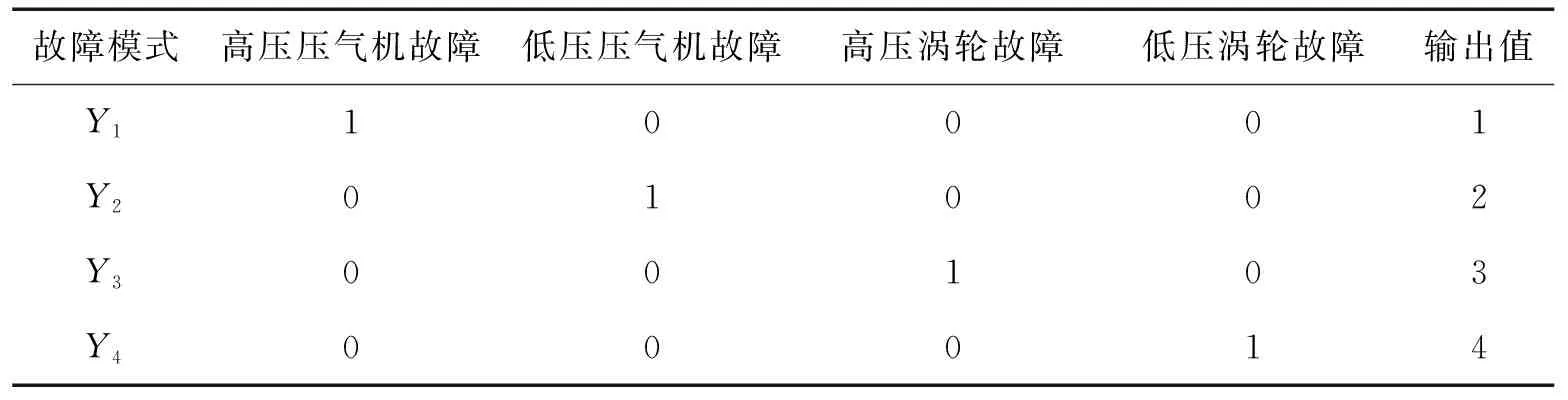
表3 故障模式

3.2 确定网络结构

根据建立的故障模型，确定该BP神经网络结构输入层是4个神经元，输出层是1个神经元。由于BP神经网络的自身局限性，无法确定隐含层的神经元数目。考虑到该数目将会直接影响输出层结果，甚至影响准确度。因此，本文依据试验数据与经验总结的公式相结合的方法，公式为

式中，m表示输入节点数目，n表示输出节点数目，a为1～10 之间的整数，l表示取值范畴的区间(1，12)。因为l的取值为1～12，所以从1至12逐个进行实验验证，算出每个节点数对应的均方误差值，均方误差表达式为

根据表4所示，当l取值为7时均方误差的值最小，说明当隐含层为7时，运算的误差最小。所以确定的网络结构为(4-7-1)型。

表4 不同隐含层的均方误差表

3.3 故障的诊断与分析

根据上述信息，基本确定网络结构模型，然后采用BP神经网络进行训练和测试。按照前面数据进行训练，网络迭代次数的精确度定为0.001，上限设为50 000步，只要程序符合其中任一条件，就会终止训练。该程序运行结果能够反映网络的运行情况，结果如图2所示。图3为BP网络训练时的误差收敛曲线，变化平稳，无较大波动，收敛情况良好。

图2 BP神经网络界面

图3 BP神经网络误差收敛曲线

根据BP神经网络的数据，判断是否达到了预期目标。为了证明所设计的BP网络结构模型准确度，采用航空公司更为成熟的Elman网络数据进行对比验证。将所采集的PW4000发动机故障数据，按照前文4个公式依次计算，然后建立相应的故障数据模型，并对数据展开训练，最后通过MATLAB软件仿真输出曲线图和预测绝对误差对比图，具体如图4、图5所示。

由图4和图5可知，BP神经网络和Elman神经网络的实际输出与期望输出曲线值很接近，两者的绝对误差也都很接近。但是，考虑到Elman神经网络会出现训练速度慢和容易陷入局部极小点的缺点，对神经网络的训练较难达到全局最优。BP神经网络的误差不仅保持在10%内，而且具备速度更快、误差率更低等优点。因此，可以验证BP神经网络更能够确定气路故障的位置。

图4 BP神经网络输出曲线图

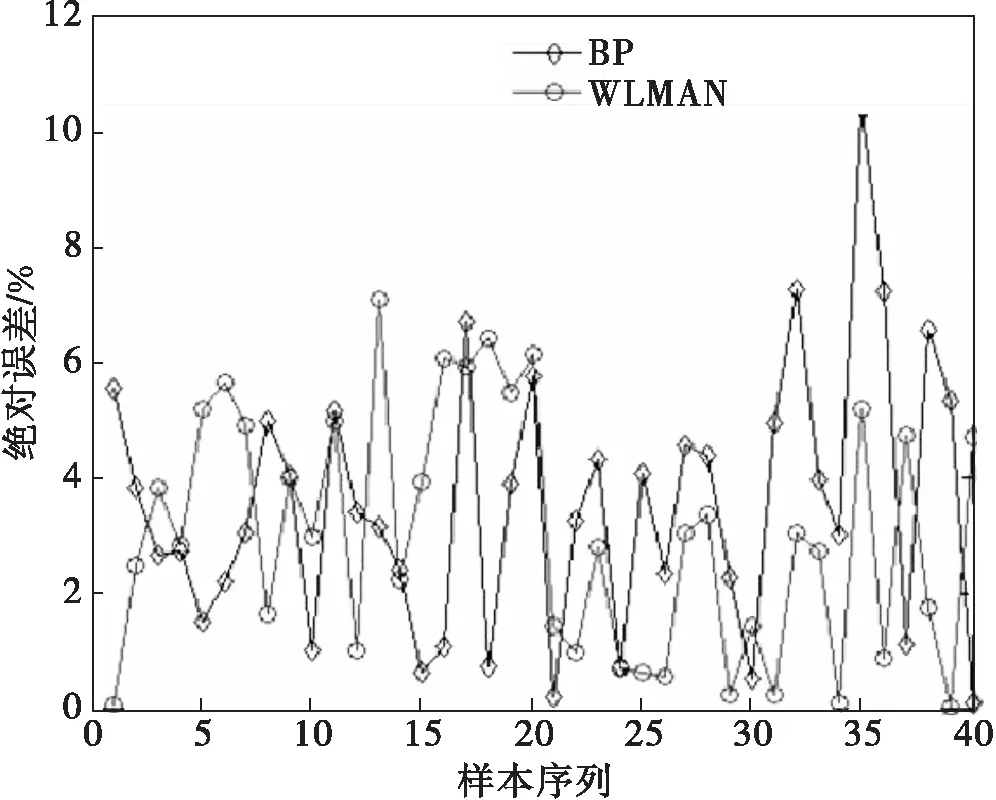
图5 BP网络和Elman网络的预测绝对误差对比图

4 结论

本文以航空公司常用的PW4000航空发动机为研究对象，以该型发动机的多种气路故障作为案例，借助MATLAB软件，对有关故障数据进行训练，通过BP神经网络和Elman神经网络的实际输出与期望输出曲线进行比较，验证了BP神经网络算法诊断速度更快、诊断结果更精确、误差率更低，更能够确定气路故障的位置，并在一定程度上弥补了其他诊断方法的不足。