地磁平静期间磁层高能粒子非垂直地磁截止刚度研究

楚伟, 秦刚, 黄建平, 许嵩, 泽仁志玛, 申旭辉

1 应急管理部国家自然灾害防治研究院， 北京 100085 2 哈尔滨工业大学(深圳)， 深圳 518055

0 引言

太阳高能粒子是由太阳耀斑和日冕物质抛射爆发时导致行星际和磁层空间粒子环境增强的事件(Le and Zhang, 2017; Le et al., 2017; Zhao et al., 2018).如果太阳质子事件中的质子能量达到相对论的能量，这些相对论能量的质子可以穿越磁层，并与地球大气发生核反应，从而使得地面仪器探测到相对论质子与地球大气发生核反应的次级成分，这种现象称为地面水平增强事件，简称Ground Level Enhancements(GLE)事件.这种事件主要出现在太阳活动高年(Le and Liu, 2020; Zhao and Le,2020).太阳高能粒子事件是偶发的，而银河宇宙线是恒定存在的，只是其强度受太阳活动的调制.银河宇宙线和太阳高能粒子进入磁层时会导致磁层高能粒子环境更恶劣，将对磁层空间的高能粒子环境产生重要的影响.高能质子能够穿透电子元件防护层导致单粒子反转，对宇航员的健康构成威胁，同时也会降低太阳能电池的寿命，影响极区短波通讯等，严重情况下将造成电子元器件损伤引发卫星故障，甚至将卫星彻底摧毁(Baker, 1998, 2001, 2002).因此研究行星际和磁层高能粒子耦合机制是日地空间物理的重点问题.

从上述公式中可以发现，当磁纬度为90°时，截止刚度达到最小.但上述公式中没有给出截止刚度与粒子投掷角的相关关系，同时后续研究人员更多地将研究内容集中在垂直方向上，即天顶方向.Smart和Shea(2005)指出，在计算真实的截止刚度时，由于行星际高能粒子的各项同性，需要考虑来自不同方向粒子的截止刚度(Masarik and Reedy, 1995).同时行星际高能粒子的投掷角作为一个重要参量(可以研究粒子的加速以及绝热聚焦效应)，对研究行星际和磁层高能粒子耦合具有至关重要的作用，因此针对行星际高能粒子的传输研究都需要考虑投掷角的扩散状况.

Shea等(1965)使用数值模拟方法研究了地球表面超过300个点的垂直截止刚度，发现在南非、南大西洋和加那利群岛附近，其截止刚度和地面观测值具有高达15%的偏差.Daniel和Stephens(1966)研究了印度的HYDERABAD台站附件的高能粒子截止刚度的方向依赖性.Bland和Cioni(1968)研究了有限方向(方位角方向15°间隔和极角方向10°间隔)的非垂直方向截止刚度，并利用两个不同观测位置(Trapani和Aire-sur-Adour)气球测量试验发现，测量和计算得到的截止刚度在上述两个不同的观测位置的均方差分别为4.8%和4.6%.Fanselow和Stone(1972)研究表明卫星实际观测结果比理论计算结果得到的垂直方向截止纬度范围通常要低3°～5°，也就意味着垂直方向的截止刚度应该不是该点的最小地磁截止刚度.Cooke等(1991)针对变化磁场引起的截止刚度变化进行了研究，并针对计算过程中只考虑粒子刚度而忽略粒子方向的做法进行了指正.Bhattacharyya和Mitra(1997)研究了截止刚度随着变化磁场的变化关系.Smart和Shea两人针对截止刚度问题做了一系列的工作(Shea et al. 1965，1968； Smart，1999; Smart et al.,1999, 2000; Shea and Smart， 2001; Smart and Shea，2003a，b，2005)，针对地面、卫星观测和数值模拟存在的偏差展开了论述，并得到在进行卫星观测和数值模拟结果精确匹配过程中需要考虑不同方向粒子入射状况的结论.Derome和Buénerd(2001)发现卫星观测到的刚度小于模拟获得的截止刚度.Shimazu等(2006)研究了行星际磁场方向对截止纬度的影响.Dorman等(2008)研究了非垂直方向的截止刚度，发现当刚度为7～8 GV时，垂直方向和非垂直方向的截止刚度相差可能达到1 GV；Dmitriev等(2010)通过POES卫星的观测数据，确定了高能粒子截止纬度的椭圆形表达式.国内研究者通过数值模拟(甄杰和楚伟，2013； Chu and Qin, 2016)和观测研究(朱邦耀，1979；乐贵明等，2003)发现地磁活动对截止刚度的影响.

由于使用解析表达式的垂直方向高能粒子截止刚度不能真实反映实际状态的磁层高能粒子截止刚度，为了尽可能准确反映真实磁层的地磁截止刚度，需要研究真实磁场状态下不同方向(投掷角)的截止刚度.

通过测试粒子的方式对不同能量(刚度)的粒子进行倒向追踪计算，得到给定点的截止刚度.由于地球磁场的结构，使用此种方法需要计算包括回旋运动在内的高能粒子运动，同时需要追踪大量的粒子运动，因此往往需要耗费大量的计算资源和计算时间，因此本文只给出地磁平静期间的典型高能粒子截止刚度状态.

1 数值模拟方法

1.1 高能粒子刚度

高能粒子刚度作为描述高能粒子能量大小的物理量，其定义如下：R=mvc/Ze，其中R表示粒子刚度，m为高能粒子质量，v为粒子速度，c为光速，Z为电荷数，e为元电荷电量.刚度在数值上等于单位单核的能量，单位为V.截止刚度表征到达给定点的最小刚度.地磁粒子截止刚度可以描述地磁场对高能粒子的屏蔽作用.Le等(2006)推导了粒子刚度和能量的关系式，依据该关系式，我们可计算不同刚度粒子的能量.图1为刚度与质子能量的关系图，从图上可以发现，两者不是简单的线性关系.

图1 质子刚度Rigidity与能量Energy的关系图Fig.1 The relationship between rigidity and energy for proton

Weygand和Raeder(2005)研究表明，使用目前通用的背景场模型都可以产生比较可靠的截止刚度模式，其中使用T96模型(Tsyganenko，1995； Tsyganenko and Stern，1996)作为外源场计算得到的截止刚度对应的纬度与卫星观测结果平均偏差为4.0°±1.4°，而使用T89模型(Tsyganenko，1989)作为外源场计算得到的数值为3.9°±2.4°，两者的偏差并不明显.由于本文研究平静期间的截止刚度状况，不采用T05(Tsyganenko and Sitnov，2005)模式，同时为了计算快捷方便，采用T89模式(Tsyganenko，1989)作为外源场.使用单粒子运动理论，结合地球磁层的内源背景场IGRF12模型以及T89外源场模型作为背景磁场，倒向追踪粒子运动状态，得到不同投掷角的粒子截止刚度，从中选择最小刚度作为给定点的截止刚度.在计算过程中，只考虑背景磁场作用，忽略电场影响，因此运动过程中粒子的能量/刚度不会发生改变.同时由于是计算行星际粒子进入磁层，不考虑回旋运动和弹跳运动的投掷角损失锥造成的影响.

1.2 模拟条件的设定

模拟过程中采用四阶龙格库塔积分，初始高度设定为450 km高度.内边界设定为1个地球半径，外边界由TS模式模型给出的磁层顶为边界.同时为了保证计算效率最大化，排除捕获粒子长时间做弹跳运动的影响，模拟过程中最大运动时长设定为1小时，最大运动距离设定为1000个地球半径，最大运动步数为106，这样既能确保计算结果的准确性，又能有效提高计算效率.

积分步长的设定将在一定程度上决定计算速度以及计算准确性.对于积分步长的设定目前主要存在两种方法.第一种方法是使用龙格库塔积分程序rkqs(Levin，1998)，设定误差范围内自适应的调节积分时间步长；第二种方法为使用粒子回旋周期的一定比例(通常情况下设定为粒子局地回旋周期的1/100，详见Smart et al., 2000；Kress et al., 2010).在本文模拟过程中，在准确描述粒子运动前提下，尽量提高粒子积分效率.我们采用第二种方法，模拟过程中时间步长设定为粒子回旋周期的1/100.由于纬度对磁场的影响远远大于经度，因此模拟过程中纬度采用1°的间隔，经度采用10°的间隔.同时鉴于目前近地空间探测器的投掷角分辨率普遍大于5°，因此投掷角采用5°的间隔，粒子初始垂直平面方向运动速度进行均匀分配(Weygand and Raeder，2005).

我们在此使用的内部场模型是国际地磁参考场(IGRF)模型，该模型是地球主要磁场及其长期变化的标准数学描述.IGRF模型针对特定年份进行了标准化处理，反映了当时可用的最精确值.为了计算内源场和外源场贡献，并进行计算过程中的坐标转换以及磁层顶外边界确认，我们使用Tsyganenko提供的软件包GEOPACK-2008.以上所有有关磁场和输入的参数均可从http:∥geo.phys.spbu.ru/～tsyganenko/modeling.html网站下载.

为了进一步提高计算效率，背景磁场使用插值进行计算，首先计算每一个格点的背景磁场，然后通过线性插值方法得到粒子运动位置的磁场强度.

2 数值模拟结果

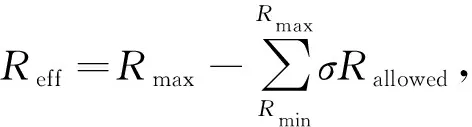
图2 计算过程中的截止刚度的半影区示意图允许(白色)和禁止(黑色)在西经40°、北纬30°垂直方向，距离地面450 km高度处，刚度计算间隔为1 MeV的最大截止刚度、最小截止刚度和有效截止刚度示意图.Fig.2 Schematic diagram of penumbra area of cut-off rigidityThe maximum, minimum and effective cut-off rigidity at intervals of 1 MeV for the calculation of the rigidity at a height of 450 km from the ground in the vertical direction of 40 degrees west longitude, 30 degrees north latitude for allowed (white) and prohibited (black).

2.1 不同投掷角截止刚度的对比

为了使研究结果具有普遍性，此研究中我们选取地磁平静期间进行模拟.

图3为截止刚度的全球分布图像，左上图为垂直方向的截止刚度分布图像，右上图为非垂直方向对应的截止刚度图像，左下图为全向的最小截止刚度图像(包括不同方向的粒子截止刚度)，右下图为垂直方向截止刚度和最小截止刚度的差值全球分布图像.对比三个全球截止刚度的分布图像，可以发现，通常所说的垂直方向(也就是天顶方向)一般意义上不是最小有效截止刚度对应的方向，尤其是在中纬度地区以及西经0～90°范围内的差值最大，差值比例可能高达60%至70%.因此如果使用垂直方向的截止刚度作为地磁有效截止刚度，将会出现普遍高估的情形.从全球平均意义来看，垂直方向截止刚度将平均高估13%左右，最大偏差将达到70%，由此可见研究不同投掷角的高能粒子进入磁层的状态对研究地磁截止刚度具有重要意义.从图4可以发现，全方向计算得到的最小截止刚度和垂直方向计算得到的最小截止刚度偏差随着纬度呈现蝴蝶状分布形态，这也意味着中纬度地区的偏差比值达到最大.

2.2 最小截止刚度对应的投掷角的全球统计

图5为最小有效截止刚度对应的投掷角的全球分布图像(为了研究方便，我们使用185°表示垂直方向角度).从图中可以发现，行星际高能粒子到达磁层的投掷角全球分布没有明显经纬度依赖性.

高能粒子的投掷角将影响高能粒子由行星际进入磁层，导致行星际高能粒子在磁层空间的分布投掷角依赖性明显.从图6我们可以发现，高能粒子由行星际空间进入磁层的最强有力的方向为沿着磁力线方向，也就是投掷角为0°或者180°时，此时高能粒子平行方向的能量巨大，可以直接沿着磁力线到达地球.同时由于研究的高能粒子能量非常高，天顶方向也是高能粒子进入磁层的一个重要通道.其他的投掷角方向分布符合中心点为90°的正态分布.

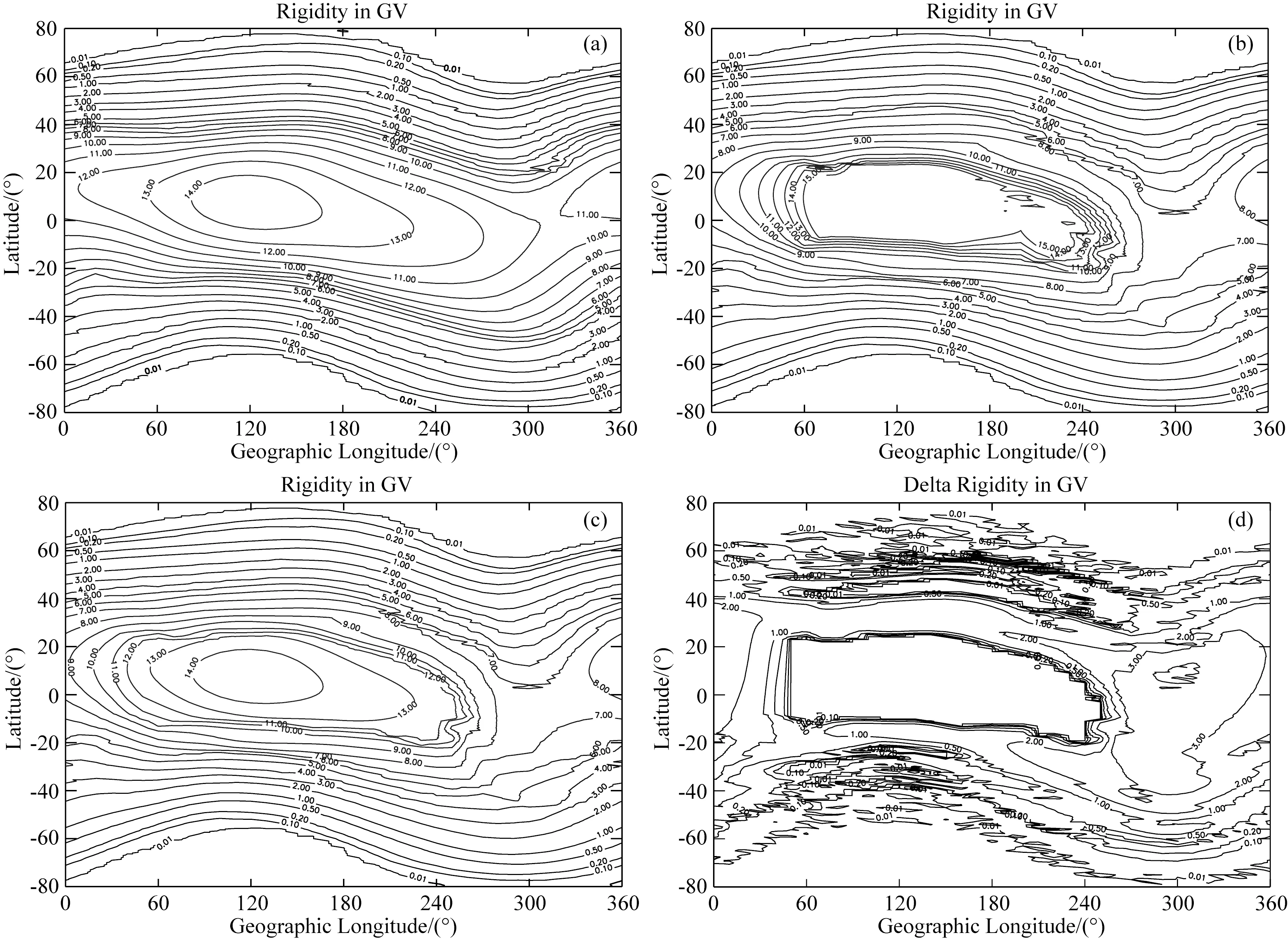
图3 高能粒子截止刚度全球分布图像(a) 垂直方向的截止刚度分布图像； (b) 非垂直方向对应的截止刚度图像； (c) 全向的最小截止刚度图像(包括不同方向的粒子截止刚度)； (d) 垂直方向截止刚度和最小截止刚度的差值全球分布图像.Fig.3 Global distribution image of cut-off rigidity(a) is vertical cut-off rigidity distribution image; (b) is non-vertical cut-off rigidity; (c) is omnidirectional minimum cut-off rigidity (including particle cut-off rigidity in different directions), and (d) is vertical direction Global distribution of the difference between the cut-off rigidity and the minimum cut-off rigidity.

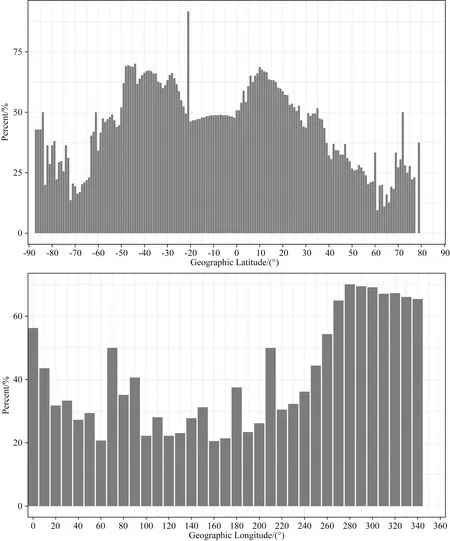
图4 截止刚度差值随着经纬度变化图像Fig.4 Cutoff rigidity difference changes with latitude and longitude

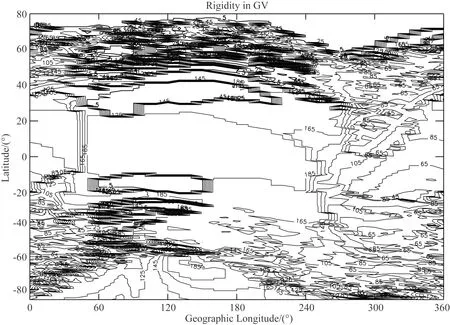
图5 最小有效截止刚度对应的投掷角全球分布图像(为了研究方便，我们使用185°表示垂直方向角度)Fig.5 The global distribution of the pitch angle corresponding to the minimum effective cut-off rigidity. (For convenience in the study, we use 185 degrees to represent the vertical direction)

图6 最小截止刚度对应的投掷角占比柱状图(为了方便问题研究，我们采用185°表示垂直方向的角度，因此图中出现185°的情形)Fig.6 The histogram of the pitch angle corresponding to the minimum cut-off rigidity (To facilitate the study of the problem, we use 185 degrees to represent the angle in the vertical direction, so the situation of 185 degrees appears in the figure)

一般假设银河宇宙线为各项同性分布，因此由银河宇宙线造成的进入磁层的高能粒子，其投掷角分布形态应呈现正态分布，此研究对磁层中高能粒子的投掷角分布具有重要作用.磁层中高能粒子的投掷角分布主要有三种可能的形态分布，各向同性分布、蝴蝶型分布以及薄饼型分布.此处获得截止刚度对应的投掷角分布图像与薄饼形态最接近，但是在两端呈现上翘的形态.

3 小结

高能粒子，尤其是行星际高能粒子进入磁层空间，将对磁层空间的粒子辐射环境产生影响.研究高能质子的截止刚度，尤其是中高纬度地区的高能粒子截止刚度，对研究行星际高能粒子在磁层空间形成的分布具有重要意义.本文使用单粒子数值模拟方法研究了近地空间高能粒子截止刚度与粒子投掷角的相关关系，研究发现：

(1)天顶方向或者垂直方向的截止刚度通常不是最小地磁截止刚度.

(2)最小地磁截止刚度对应的投掷角方向最大为沿着磁场方向，即0°方向；其次为天顶方向，也就是通常所说的垂直方向；然后为180°方向，即与磁场反方向.这种高能粒子进入磁层的投掷角分布状态符合理论预期，因为沿着磁力线方向是粒子最容易进入磁层的方式，因此对应的截止刚度比较小.

(3)全球范围截止刚度对应的投掷角分布符合两端上翘的正态分布形态，不考虑两端最大占比，中心位置出现在90°附近.

(4)通过地磁平静期间的数值模拟发现，使用垂直方向的截止刚度对比最小截止刚度平均将高估13.17%，最大可能高估70%.

(5)不同经纬度高能粒子的截止刚度与投掷角不存在明显关系.

本文使用了数值模拟方法进行高能粒子的运动模拟，由于使用的背景磁场和磁层顶边界模型的不尽精确，得到的结果可能不能完全反映到达近地空间最小的高能粒子刚度，但能反映截止刚度的总体趋势.为了得到更普适的截止刚度模式，在将来工作中，我们将利用数值模拟结合卫星观测数据，进一步修正不同经纬度的高能粒子截止刚度，以期做到尽可能精确可靠，为研究近地空间高能粒子环境变化提供精确的背景模型(Wang et al. 2020).随着我国第一个电磁监测试验卫星的成功发射，星上搭载的高能粒子探测器将对近地空间高能粒子展开轨道高度全球范围、高投掷角分辨率的高能粒子探测数据，将有利于对此问题进行更加精确的研究.Rodger(2006)使用地基观测数据和理论预期进行了对比，发现在磁扰动期间(Kp指数小于5的情况下)观测和理论预期符合得很好，但是当Kp指数大于7，理论预期要比实际观测结果大很多.我们后续将针对扰动条件下不同方向的截止刚度展开研究，届时将对比平静期间与扰动期间的变化磁场导致的截止刚度变化状况.

致谢本研究得到了国家重点研发专项-地球物理探测卫星数据分析处理技术与地震预测应用研究(2018YFC1503502-05)课题、地震活动期间ZH-1电离层掩星数据异常研究(ZDJ2019-03)课题以及ISSI-BJ(2019IT-33)课题的支持，同时得到了组内各位同事的鼎力帮助，在此感谢同事们的辛勤付出，使得本文得以完成.感谢IGRF提供的内源场源代码以及Tsyganenko提供的外源场模型源代码.同时在此对审稿老师提出的宝贵建议表示感谢.