融合MLP和DBN的光伏发电预测算法

徐先峰，蔡路路，张 丽

长安大学 电子与控制工程学院，西安710064

随着大规模的光伏并网，光伏输出功率自身的不稳定性、波动性和间歇性对电网的稳定运行及调度管理带来诸多问题[1-2]。精确的光伏发电预测对于优化电网运行，提高系统可靠性，保证电能质量，提高光伏发电站运行、管理及发电效率具有重大意义[3-4]。

国内外对于光伏发电预测模型的建立进行了大量研究。目前按照预测方式可将光伏发电预测方法分为直接预测和间接预测[5]。前者直接对光伏发电系统的输出功率进行预测，常用的预测模型主要有支持向量机（Support Vector Machine，SVM）[6]、自回归积分滑动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）[7]等；后者先对太阳辐射强度进行预测，再利用发电系统模型预测输出功率，主要有基于数值天气预报预测法[8]、基于云图预测法[9]等。直接预测虽简洁方便，但需基于历史发电数据直接预测输出功率，其准确性依赖于预测算法以及是否有大量准确的历史数据。间接预测对太阳辐射强度和输出功率分别进行建模预测，建模方法具有一定的灵活性，但两个预测模型的建立提高了预测成本，并存在着预测误差叠加的问题。

近年来，深度学习由于其强大的建模能力和显著的预测能力备受关注[10]，也逐渐应用于光伏发电预测之中。目前使用较多的预测模型主要有长短期记忆网络（LSTM）[11]，多层感知器（MLP）[12]和深度信念网络（DBN）[13]。

作为典型的深度学习算法，LSTM在处理与时间序列相关的问题中，如股票预测[14]、负荷预测[15]、风电预测[16]等，均表现出十分优秀的预测性能，已成为评测深度学习新算法性能的参照标准[17]。MLP 克服了传统感知器难以解决非线性问题的弱点，并且具有较强的非线性映射能力、泛化能力和容错能力，但模型收敛速度较慢，学习效率低，对于复杂性问题预测精度不高。DBN虽然能够有效预测处理大量复杂数据，但由于需要进行逐步分层预训练，学习时间较长，且若参数选择不当极易陷入局部最优问题。

为了综合利用MLP算法较强的非线性问题解决能力以及DBN 算法有效处理大量复杂数据的优势，构建高精度的光伏发电预测模型，本文在深入分析MLP 算法及DBN算法的基础上，提出了一种融合MLP和DBN的预测算法（MLP-DBN），首先利用MLP模型进行初步预测，继而将预测值与实际值间的残差输入DBN 模型预测，最终利用残差预测值对MLP 模型的预测值进行修正。本文利用光伏发电实测数据，基于Keras 平台进行了仿真，探究了不同学习率对模型预测性能的影响，并对模型中各参数进行了寻找设置。最后通过性能指标对MLP-DBN算法进行了性能评估。仿真结果表明，与传统的预测算法SVM 以及典型的深度学习算法LSTM 相比，MLP-DBN 算法的各项性能指标均有较大改善，可以有效进行光伏发电预测。

1 MLP-DBN融合算法

1.1 MLP-DBN模型

MLP-DBN 融合算法模型训练的基本思想是：首先将待预测光伏数据输入模型，利用MLP 模型进行初步训练并得出发电预测值；计算出预测值与实际观测值之间的残差，将残差输入DBN模型进行训练，得出残差预测值；模型训练完成后，用DBN模型得到的残差预测值对MLP 模型得到的预测值进行修正，得到最终光伏发电预测值。模型训练过程如图1所示。

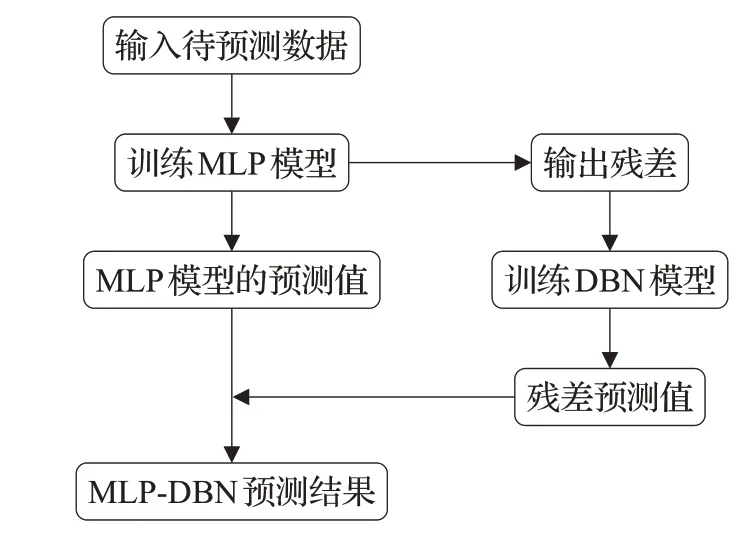
图1 MLP-DBN模型训练流程图

具体的算法流程如下：

（2）利用MLP模型进行训练并预测，得出发电预测值Y′。

（3）计算上一步中预测值与实际观测值间的残差Residual=Y′-Y。

（4）将MLP模型得到的残差Residual输入DBN模型中进行训练，得出残差预测值Residual′。

（5）修正MLP模型得到的预测值，得出最终发电预测值Y_final=Y′+Residual′。

MLP-DBN预测模型结构如图2所示。其结构主要由MLP模块和DBN模块组成，MLP模块将待预测光伏数据进行初步训练后预测，输出发电预测值；DBN模块将根据MLP模块得到的残差进行训练后得出残差预测值并输出。最后利用DBN 模块输出的残差预测值对MLP 模块所得发电预测值进行修正，从而得出最终发电预测值。

图2 MLP-DBN模型结构图

1.2 MLP模块

MLP 模块的作用是利用光伏发电实测数据进行初步预测，以便利用预测值与实际观测值进行残差计算。其输入层的输入数据为光伏发电功率数据，输入层接收数据后将数据传至隐藏层，在隐藏层内将数据进行分析处理后再传至输出层，最后在输出层内对数据进行处理后输出。

具体的预测过程如下：

假设MLP 预测模型的输入为n维向量X=[x1,x2,…,xn]，数据在隐藏层内进行分析处理后，其输出由下式得出：

其中Wh与bh代表权值和偏置。

输出层将数据进行最终处理后输出，由下式得出：

1.3 DBN模块

DBN模块的作用是利用MLP模块得出的预测值与实际观测值间的残差进行预测。第一个RBM的可视层接收输入数据，即MLP 模型得到的预测值与实际值之间的残差，之后将其传入下层隐含层。隐含层将数据的特征信息进行提取并输出至下一个RBM 的隐含层，以此逐层向上进行训练直至最后一层隐含层，其中前一个RBM 的隐含层作为下一个RBM 的可视层。最后一个RBM 将数据传入顶层的输出层，通过在顶层添加标签数据，利用BP算法对整个网络进行微调。

具体预测过程如下：

（1）将输入向量X赋给可视层V1，利用下式计算出使隐藏层中每个神经元被开启的概率：

其中，b代表可视层的偏置，σ代表sigmoid函数。从计算出的概率分布进行Gibbs抽样：

（2）利用H1构造下一个RBM 的可视层，计算使可视层中每个神经元被开启的概率：

其中，a代表隐藏层的偏置，计算概率密度后进行Gibbs抽样：

（3）更新权值和偏置。

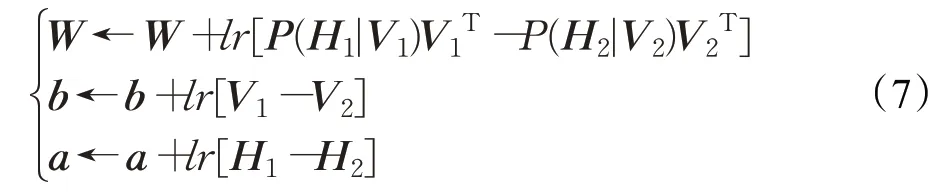
其中，lr代表学习率。

（4）利用BP 算法微调网络的权值，最小化目标函数，目标函数为均方误差：

（5）根据理想输出进行预测。

2 实验仿真

2.1 实验运行环境及数据处理

本次实验在Keras2.4 环境下进行。选择的数据集来自GECAD 光伏系统的数据库[18]，数据集内数据包括日期时间和发电量，采样周期为1 min，采样时间为2016年7月27日到2016年11月16日，共157 178个样本，并将数据集前70%的数据作为训练集拟合模型；数据集后30%的数据作为测试集进行预测，以测试算法性能[19]。

由于数据集内数据具有稳定的变化趋势且不存在极端的最大最小值，为了确保数据的有效性，消除指标之间的量纲影响并得到更准确的数据分析结果，需要将数据按下式进行归一化处理[20]。

其中，xmax为数据集中的最大值，xmin为数据集中的最小值。

2.2 性能评估指标

为了评估各预测模型的性能，本文选用了均方根误差（RMSE）、平均绝对误差（MAE）和决定系数R2作为性能评估指标。各性能指标表达式如下：

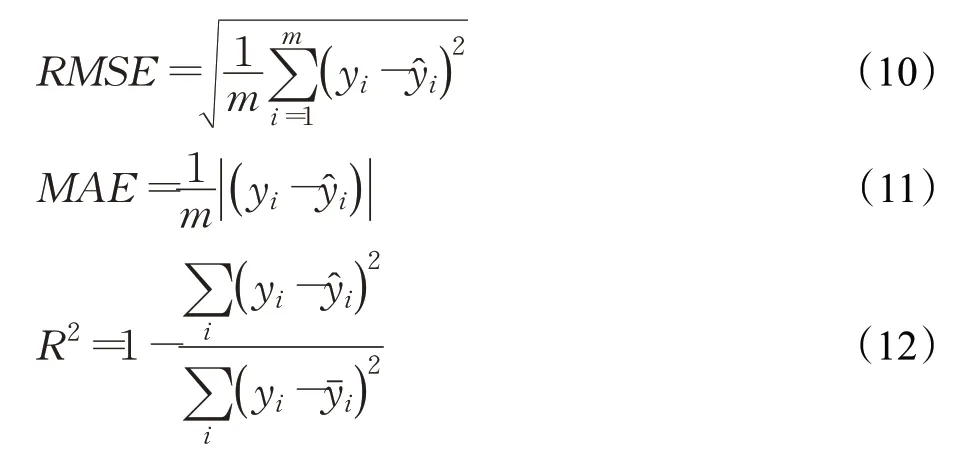
其中，yi代表真实值，代表预测值，代表真实数据的平均值，即

2.3 MLP-DBN模型的输入及输出

MLP-DBN模型的输入数据为来自GECAD光伏系统的光伏发电历史功率数据，如图3所示。

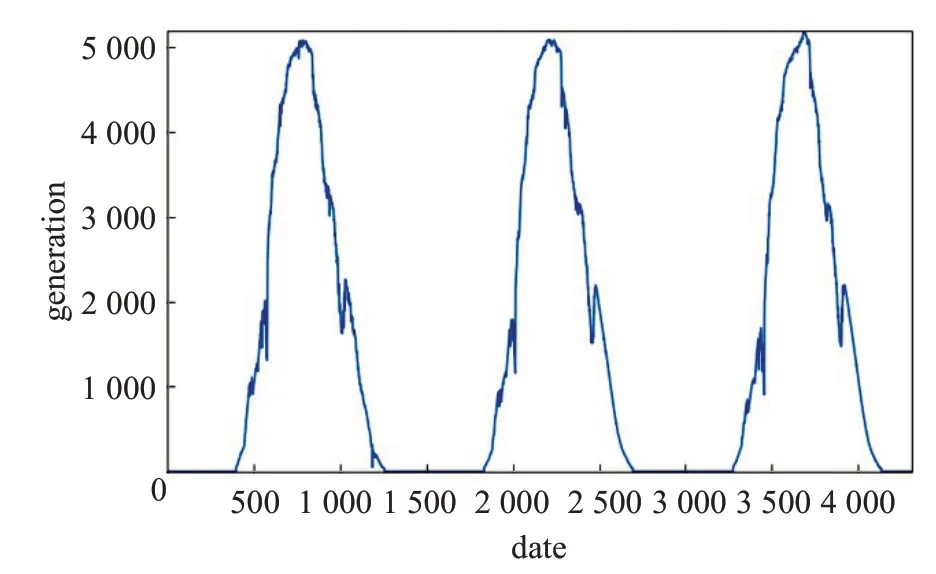
图3 光伏发电历史数据

首先将输入数据通过公式（9）进行归一化处理。将数据归一化后可以消除量纲影响，方便数据处理，其次可以加快模型收敛速度，提升模型性能。归一化处理后的数据如图4 所示。将处理后的数据输入MLP-DBN模型，即作为MLP 模块的输入数据。数据输入MLP 模块后，经过训练学习输出数据，得出初始预测值，如图5所示。

图4 MLP模块的输入数据

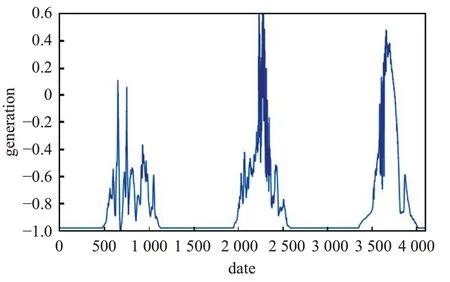
图5 MLP模块的输出数据

将MLP模块得到的初始预测值与观测值进行残差计算，将其输入DBN 模块，即将MLP 模型的输出数据进行残差计算后作为DBN 模块的输入数据，如图6 所示。DBN 模块经过训练学习后输出数据，得出残差预测值，如图7所示。使用DBN模块得到的残差预测值修正由MLP模块得到的初始预测值，即利用DBN 模块的输出数据修正MLP模块的输出数据，得到最终预测值，则MLP-DBN模型预测结束。

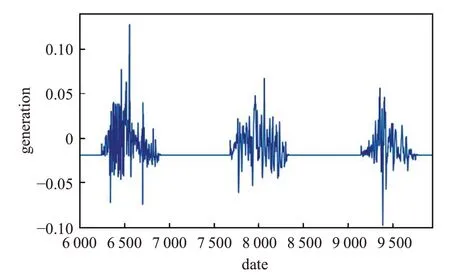
图6 DBN模块的输入数据

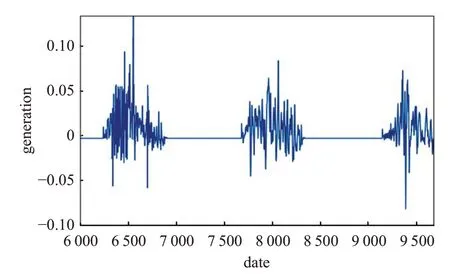
图7 DBN模块的输出数据

2.4 MLP-DBN模型参数设置

为了提高模型收敛速度，减少训练过程中学习率的手动调节，预测模型采用Adam 优化器[21]。学习率（Learning Rate）是指在优化器中更新网络权值时的幅度，在训练神经网络模型时，学习率的设置对于网络的学习速度和效率起着重要作用。本算法需对MLP 和DBN 分别进行建模，并需分别设置初始学习率，因此学习率对于本模型的预测性能有关键性影响。为寻找合适的初始学习率，本实验在引入Dropout[22]以防止出现过拟合问题的基础上，对学习率的设置进行了如下实验：

case1 MLP模型与DBN模型学习率均设为0.01。

case2 MLP模型设为0.01，DBN模型设为0.005。

case3 MLP模型设为0.01，DBN模型设为0.001。

case4 MLP模型设为0.01，DBN模型设为0.000 5。

case5 MLP模型设为0.01，DBN模型设为0.000 1。

case6 MLP模型设为0.005，DBN模型设为0.000 1。

case7 MLP模型设为0.001，DBN模型设为0.000 1。

case8 MLP模型设为0.000 5，DBN模型设为0.000 1。

case9 MLP模型与DBN模型均设为0.000 1。

各组合下的预测结果如图8所示。

实验表明，当学习率设置过大时，损失函数将出现大幅度震荡，无法有效收敛。适当减小学习率可使得模型的损失减小，并且有效改善预测模型的性能。但当设置过小时，对预测性能影响不大，反而使得模型训练时间增长。在仔细观察各学习率下的损失函数曲线图以及性能指标的基础上，发现当MLP 的学习率设置为0.001 以及DBN 的学习率设置为0.000 1 时，损失函数表现良好，性能指标最优，且训练时间最短。因此最终确定MLP模型的学习率为0.001，DBN模型的学习率为0.000 1。

图8 不同学习率下的预测结果对比图

实验表明，学习率的优化设置对于解决MLP 收敛速度慢，学习能力较差以及DBN 学习时间较长的问题有一定的改善，为了进一步克服两者的缺点，本实验采用试错法对可改善以上问题的模型参数，包括批大小（batch_size）、激活函数等进行了寻找优化设置。参数寻找过程为首先根据经验值分别设定MLP 及DBN 模块的初始参数值[23-24]，通过观察模型的训练时间以及性能指标，反复修改模型中的参数，不断优化模型的训练时间及性能指标。直至模型训练时间以及性能指标表现最优时，便将所设置参数确定为最终参数。各参数下模型测试结果如表1、表2所示。

表1 MLP测试结果

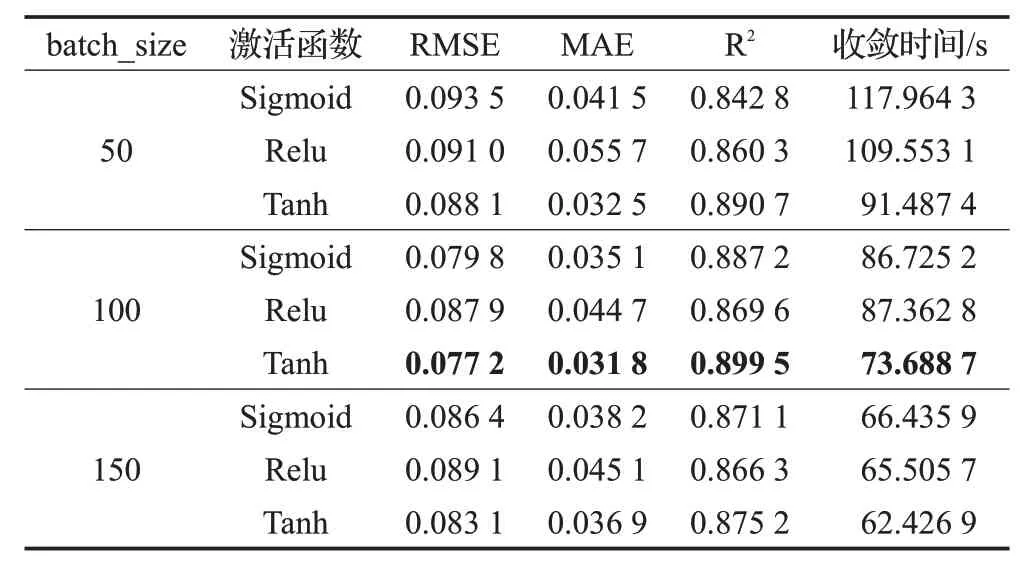
表2 DBN测试结果

由各参数下模型的测试结果可以看出，虽然batch_size 增大时可有效减少训练时间，但是较大的batch_size 将使得模型的预测精度降低。另外，对于MLP模块，当其激活函数选择Relu时，将使得模型的训练时间减少，并且相比于其他激活函数有较高的预测精度。对于DBN模块，当其激活函数选择Tanh时，相比于其他激活函数，DBN模块的训练时间较短，并且此时的预测精度较高。故最终将MLP 模块的batch_size 设为150，激活函数选择Relu；DBN 模块的batch_size 设为100，激活函数选择Tanh。此参数的选择使得MLP 和DBN的学习能力显著提高，从而提高MLP-DBN模型的性能。

模型其余参数同样采用试错法，通过观察训练时间及性能指标，经过反复实验后，确定了模型的最终参数。具体参数设置如表3所示。

表3 模型参数设置

2.5 仿真分析

SVM 作为传统的机器学习算法，被广泛应用于光伏发电预测问题中，并具有较高的准确性，但当数据集较大时，训练时间较长，且预测性能将受到一定制约[25]。为验证MLP-DBN算法的有效性，本文选取SVM算法和LSTM算法进行对比，同时将算法与单一的MLP算法及DBN算法进行对比，以此对MLP-DBN算法进行评估。各对比模型参数设置如表4所示，SVM模型的核函数采用Linear。预测仿真结果如图9 所示（True 代表真实值，SVM 为SVM 模型，DBN 为单一的DBN 模型，MLP 为单一的MLP 模型，LSTM 为LSTM 模型，MLP and DBN为MLP-DBN模型）。

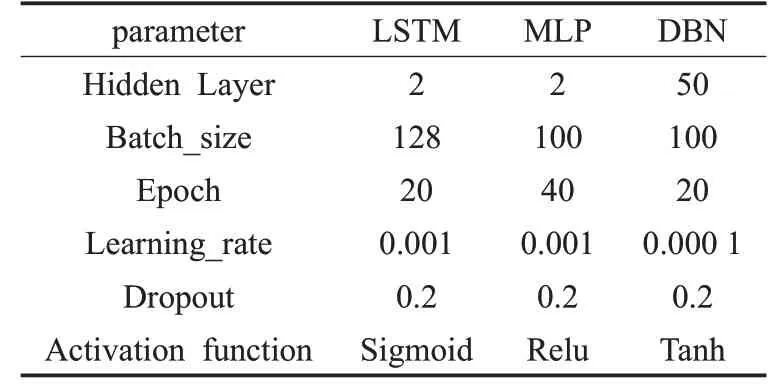
表4 各对比模型参数设置

图9 各预测算法的仿真结果

各预测算法的RMSE、MAE、R2、训练时间以及测试时间如表5所示。

表5 各算法性能指标对比表

仿真结果表明，SVM 预测算法在发电量谷值时具有较大的偏差且测试时间较长，而LSTM预测算法虽具有较高的预测精度，但在发电量谷值时预测偏差也较大，训练与测试时间也相对较长。而MLP-DBN模型得到的预测值与实际值十分接近，并且变化趋势一致，在发电量峰值和谷值时都有较高的预测精度。通过比较MLP-DBN算法与SVM、LSTM、MLP、DBN算法的性能指标表明，MLP-DBN算法的RMSE分别降低了2.20%、1.64%、2.09%、4.83%，MAE 分别降低了0.67%、0.11%、1.12%、1.30%，R2分别提高了2.96%、2.05%、2.77%、8.64%，各项预测误差均有明显改善，大幅度提高了预测精度。虽然MLP-DBN 的训练时间相较SVM 算法较长，但是其测试时间相比各算法均有一定的优化。

3 结论

本文利用深度学习方法实现了光伏发电预测，并提出了一种将MLP 和DBN 相结合的MLP-DBN 算法，通过对比MLP-DBN 算法与其他算法的性能指标和仿真结果表明，与单一的MLP预测模型和单一的DBN 预测模型相比，MLP-DBN 模型的预测效果有较大的提升。与传统的预测算法SVM模型以及具有较强预测能力的LSTM 预测模型相比，MLP-DBN 模型的性能指标均有明显的改善，说明MLP-DBN 具有优秀的预测精度，有利于解决光伏发电预测问题。虽然测试时间相比其他算法有一定的减短，但是模型的训练时间较长，故未来可对模型的训练及测试时间进行改善，另外可考虑采用其他方法进行参数调优，进一步提高模型的精度。