基于数字信号处理器实现特定消谐脉宽调制控制技术的研究*

曾桂珍 曾润忠 张广远

（1.华东交通大学机电与车辆学院，330013，南昌；2.华东交通大学土木建筑学院，330013，南昌；3.中车大连电力牵引研发中心有限公司，116022，大连∥第一作者，副教授）

在大功率交流传动高速发展的今天，谐波对用电设备的危害也变得愈发严重。传统的PWM（脉宽调制）方法无法消除或抑制谐波的发生。谐波不仅会造成牵引电机定转子发热、转矩脉动，还会污染设备的电磁环境，降低系统的稳定性［1］。特定次谐波消除脉宽调制（SHEPWM）技术，是由美国PATELH S和HOFTR G 教授提出的一种优化PWM 技术。它主要是通过优化算法对脉冲开关导通角进行选择，来有效减少输出中的低次谐波分量，实现特定次谐波的消除，以减小因谐波引起的转矩脉动［2］。

本文以三相电压型逆变器为分析对象，先根据SHEPWM 控制技术的基本原理建立数学模型，推导出特定谐波消除中开关角与调制度之间的关系；然后利用Matlab 软件工具对该非线性关系方程组进行求解，同时得到不同载波比下对应的PWM 单相电压脉冲输出波形及FFT（快速傅里叶变换）分析，来验证算法的正确性；最后利用dsPACE 仿真平台数字化实现SHEPWM 控制技术，同时对基于数字信号处理器（DSP）实现的SHEPWM 控制技术进行试验验证，分析输出电压、电流在不同载波比下谐波消除情况，以此来证明本文所提出的基于DSP 实现的SHEPWM 控制技术能够有效消除低次谐波、减小电流脉动，并提高电能控制质量。

1 SHEPWM 控制技术的基本原理

SHEPWM 控制技术的基本原理是在逆变器多次换向中，恰当地控制输出相电压波形使其存在特定的缺口，即使其不存在某些特定的谐波。一般来说，在半个周期的电压波形中每设定一个缺口，就可以消除一种谐波。但是在控制电压输出时，必须要满足波形在正负半周零点对称和半周内π/2 对称。这样使得输出电压波形为奇函数，不存在偶次谐波和余弦量，使谐波含量达到最少。以单相双极性SPWM（正弦脉宽调制）为例，假设当开关角αi满足式（1）条件［3］，得到其电压波形如图1 所示。

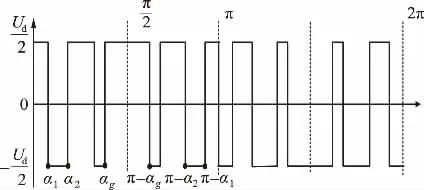
图1 单相双极性SHEPWM 输出波形

从图1 中得知：该电压波形在半个周期内以π/2 为中心镜像对称，在一个周期内以π 为中心旋转对称，这样就满足了SHEPWM 输出波形的基本要求［4］。本文对该双极性PWM 波形进行傅里叶变换分析，设ao为直流分量、an为余弦分量、bn为正弦分量、n 为谐波次数、ω 为旋转的角频率、t 为时间，则可得到图1 所示波形的输出电压U（0t）傅里叶分解表达式为：

根据SHEPWM 控制技术基本要求，该波形在［0，2π］域对π 点为中心对称，在［0，π］域对π/2 点为轴对称。因此式（2）满足式（4）条件：

将式（4）代入式（2）即可求出傅里叶级数的ao、an、偶次正弦分量bo和奇次正弦分量bj分别如式（5）所示：

式中：

N——［0，2π］区间的脉冲数，又叫载波比；

（N-1）/2——一个周期内开关角个数，本文用NK表示；

αi——［0，2π］区间内的NK个开关角中的第i个开关角。

从式（5）可知，SHEPWM 波形的ao、an、bo都为零［5-6］。所以傅里叶变换后U0（t）表达式可简化为：

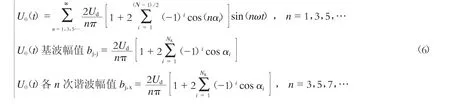
从式（6）可知，各次bj，x是与αi有关的函数，只 要求得各个αi大小使得bj，x=0，即可消除频率为n次的谐波量。根据电动机结构连接方式特点，电动机自身可以消除线电压中3 的倍次谐波，所以SHEPWM 控制技术中重点消除的谐波次数为5，7，11，13，…。根据理论总结可知，单位周期内N个调制脉冲可消除NK-1 种谐波，可消除的谐波次数为n=6K±1［5］。其中：K 取值范围为[1，NK-1]，且当NK为奇数时，n 最大可以取到3NK-2；NK为偶数时，n 最大可以取到3NK-1。

根据电机控制理论，由于Ud一般固定不变，电机输出电压的大小可以用调制度m 来衡量，其中m定义为bj，j与π/2 倍Ud的比值。

所以由式（6）和式（7）得知，假设需要消除低次谐波，就需要bj，x=0。那么SHEPWM 控制技术的αi与m 之间的数学模型表达式为［6-7］：

2 Matlab 软件模拟αi 计算及电压波形分析

根据上述各式可知，SHEPWM 控制技术的αi与m 存在一定关系。但所得的方程组为多变量非线性超越方程组，求解难度大、结果也并不唯一，无法直接得到实时解。所以，本文利用Matlab 软件编写相应的m 函数，选定初值后，利用迭代的方法对不同载波比下SHEPWM 的αi与m 进行离线求解，并根据求解结果对SHEPWM 输出的单相电压脉冲波形进行分析，以验证算法求解后的正确性。

在Matlab 软件的非线性方程组函数求解中，合理选择初始值有助于迭代算法能够快速收敛，SHEPWM 的初始αi分布范围主要包含0° ～60°和0°～90°两种。本文采用初值选择在0°～60°范围内进行求解。其中初始αi选择公式为［6-7］：

在大功率交流传动控制系统中，受到开关器件损耗和散热问题的影响，PWM 的载波比都很低。为了保证输出电压正弦度、减小负载电机转矩脉动、降低开关损耗，一般在低速情况下逆变器输出采用异步调制；中、高速情况下，逆变器输出电压采用分段同步调制。其中异步调制区载波比相对较高，谐波含量小，无需再进行特定次谐波消除［8］。同步调制区谐波主要集中在载波比为11、7、5 分频中，SHEPWM 谐波消除的意义重大。本文根据实际应用情况，以载波比11 分频为例，利用式（8）和（9）得到11 分频下SHEPWM 的αi与m 之间的非线性方程式，同时利用Matlab 软件编写对应的.m 函数，对载波比11 分频的非线性方程组进行求解，得到其m和αi的关系（见图2）和单相电压脉冲谐波（见图3）。

图2 载波比为11 时m 与αi 的关系图

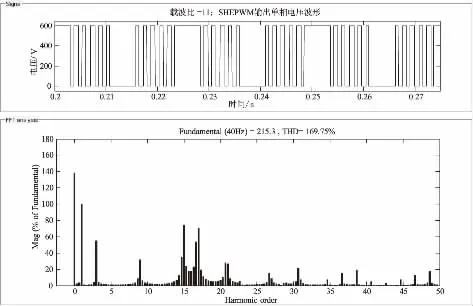
图3 载波比为11 时单相电压谐波截图

设定Ud=600 V、11 分频时电压输出频率fout=40 Hz、m=0.57。从图3 中可以看出，当载波比为11时，5、7、11、13 低次谐波基本消除。同理设定7 分频的m 为0.75、输出电压频率为52 Hz，5 分频的m 为0.86、输出电压频率为60 Hz，可以得到载波比为7、5 分频下其m 和αi的关系和单相电压谐波分别如图4 ～7 所示。

根据SHEPWM 消谐理论，单位周期内N 个调制脉冲可将NK-1 种谐波消除，可消除的谐波次数为n=6K±1。从Matlab 软件对不同载波比下单相电压脉冲波形的FFT 分析结果可以看出：SHEPWM在载波比等于11 时，基本消除了5、7、11、13 次谐波；在载波比等于7 时，消除了5、7 次谐波；在载波比等于5 时，可以消除5 次谐波。通过以上分析计算可知，通过Matlab 软件的迭代运算，所得到的m 和αi的关系能够实现SHEPWM 对特定次谐波的消除，验证了算法的可行性。

图4 载波比为7 时m 与αi 的关系图

图5 载波比为7 时单相电压谐波截图

图6 载波比为5 时m 与αi 的关系图

图7 载波比为5 时单相电压谐波截图

3 仿真和试验

为了深入研究SHEPWM 对谐波消除的实际情况，本文利用美国TI 公司提供的DSP 控制芯片TMS320F28335，编写软件语言对SHEPWM 进行数字化实现，并下载到该控制芯片当中；同时针对该芯片搭建配套的硬件电路，结合dsPACE 半实物仿真平台对SHEPWM 的PWM 波形进行硬件实现；最后利用试验平台带负载电机运行，验证SHEPWM在实际应用中谐波消除情况。

为保证试验数据统一，本文在dsPACE 半实物仿真平台和最后试验中使用相同的电机参数。其中异步电机参数如下：定子电阻Rs=0.038 1 Ω，定子漏感Lls=0.525 8 mH，转子电阻Rr=0.028 8 Ω，转子漏感Llr=0.945 1 mH，互感Lm= 19.479 mH，电机转动惯量J=0.2 kg·m2；电机的额定功率Pn=435 kW，额定频率fn=31 Hz，额定线电压Un= 800 V，额定转矩为6 800 Nm。逆变器直流电源电压为1 800 V。

为降低开关损耗、提高电压利用率、减小不同载波比之间相互切换过程中的电流冲击，本仿真和试验在电机低速区采用异步调制，中高速区采用分段同步调制的方式。其中，分段同步调制区包括11 分频、7 分频和3 分频，最后经过3 分频自然过渡到方波工况。根据上述SHEPWM 基本理论，载波比为3分频和方波工况时与普通PWM 一样不能进行谐波消除，所以本文主要研究电机控制运行在11 分频和7 分频时，对SHEPWM 进行dsPACE 半实物仿真分析和试验验证。其中dsPACE 半实物仿真结果如下：图8 给出了在11 分频和7 分频情况下电机定子磁链轨迹，从图中可以得知定子磁链受PWM 脉冲控制为规则对称的多边形，磁链控制无畸变，磁链值约为2.4 Wb；图9 给出了11 分频情况下电机输出电流和相电压波形，从图9 中可以看出电机输出电流稳定且无震荡，其有效值约为290 A，相电压输出正弦度良好，软件分析其相电压有效值约为620 V。

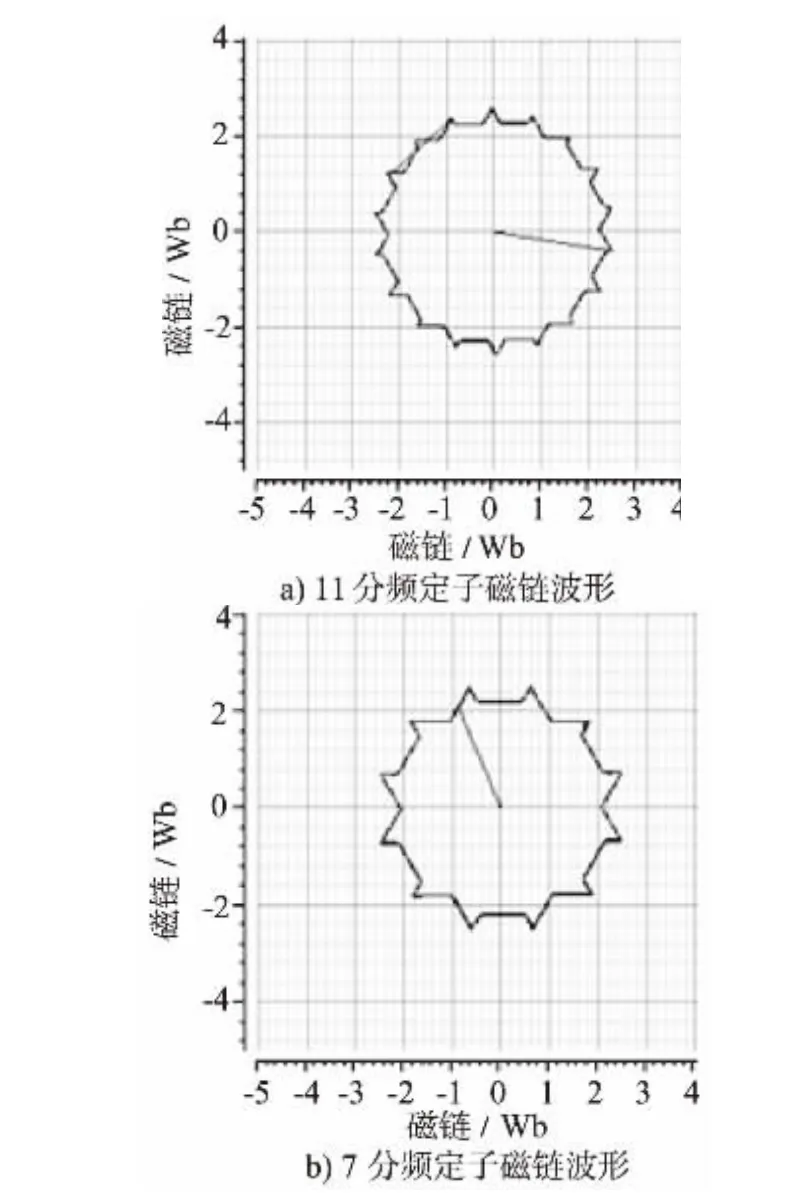
图8 电机定子磁链波形

图9 11 分频下电机输出电流和相电压波形

从半实物仿真结果可以看出，通过DSP 可数字化实现SHEPWM，能够达到控制电机在全速度范围内稳定运行。其电流输出平衡稳定，转矩脉动小。根据半实物仿真情况，搭建大功率交流传动机车试验平台，验证该算法在实际应用中的情况，具体波形和数据结果如下：

图10 分别显示了在实际运行中电机线电压和电流波形。从图10 波形中可以看出SHEPWM 同步调制在11 分频（0 ～0.06 s）和7 分频（0.06 ～0.12 s）工况下运行时，电机电压输出稳定、电流平衡；在两者进行切换时，电机电流运行稳定、冲击很小，电压波形输出正常。从图10 电流波形看，因为7 分频的PWM 电压输出脉冲数减小、电流波形波动较大，所以11 分频的电流波形平滑度要优于7 分频，其整体谐波含量也偏小。

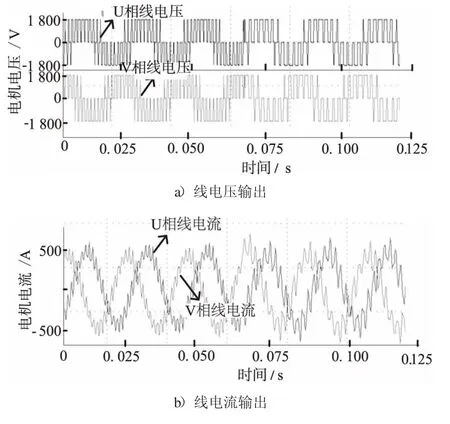
图10 线电压和电流输出波形

为了分析实际运行中电机输出电流的谐波含量，本文将切换前后的电流数据导出，利用FFT 工具进行谐波分析。其中示波器采样周期为100 μs，选取导出的波形长度时间均为0.1 s，其电流输出基波频率为49.751 Hz。从图11 中经FFT 分析可知：在11 分频时，电流的5、7、11、13 次谐波都基本消除，谐波从17 次开始增加；在7 分频时，电流的5、7次谐波被消除，谐波从11 次开始增加。两者切换前后的输出电流基波大小基本相同，但由于7 分频的载波比较小，谐波整体含量略高于11 分频。

从试验运行波形来看，基于DSP 实现的SHEPWM 在实际运行中的电机运行稳定，电压和电流波形良好，转矩脉动较小；从对电流波形的FFT分析可以看出，在全速度范围内，SHEPWM 能够有效消除其特定的低次谐波含量，可提高电压利用率、减少转矩脉动。

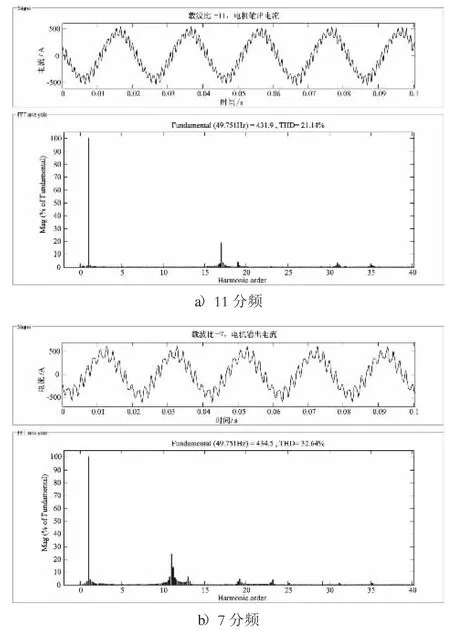
图11 输出电流谐波分析截图

4 结语

本文通过深入分析SHEPWM 控制技术的基本原理，对特定谐波消除中αi与m 之间建立相应的数学模型；然后，利用Matlab 软件对该数学模型在不同载波比下进行求解，得到对应的PWM 单相电压脉冲输出波形，并进行FFT 分析验证算法的正确性；最后利用dsPACE 半实物仿真平台及试验，对基于DSP 实现的SHEPWM 控制技术进行验证。试验通过对电机输出转矩、电压和电流的波形分析，证明了本文所提出的基于DSP 实现特定消谐PWM 控制技术能够有效消除电流中的低次谐波、减小电流脉动、提高电压利用率，可为后续深入研究谐波对交流传动控制系统的影响提供参考。