对启动压力梯度和压敏效应的反思、推导与评论

陈元千，刘 攀,2，雷丹凤

（1.中国石油勘探开发研究院，北京100083；2.中国地质大学（北京）能源学院，北京100083）

Bear[1]和Fatt[2]利用室内岩心模拟的测试资料，分别于1972年和1952年提出了启动压力梯度和压敏效应。在2000年以后，随着鄂尔多斯盆地致密低渗（K=0.1～10 mD，1 mD=0.986 9×10-3μm2）油气藏的开发，启动压力梯度和压敏效应被中国有关专家学者视为两大重要课题，列入国家重点基础研究发展项目（973计划）、国家重大科技项目和国家自然科学基金项目等。大量的室内模拟实验研究表明对于低渗砂岩储层启动压力梯度和压敏效应是存在的。在近二十年间，尽管发表了诸如文献[3～32]的数百篇文章，但在理论上并没有太大的进展，仍停留在初期的感性认识阶段。甚至，将线性流的常数启动压力梯度直接用于平面径向流方程。同时，还将压敏效应直接用于产量公式。这些不正确的做法，在近一两年的期刊上仍然可见[30-32]，因此，可以说已到了必须指出和改正的时候。

1.对启动压力梯度的反思与推导

Bear[1]于1972年，通过利用一维岩心进行室内模拟实验，研究低渗透地层达西定律应用的下限时，提出了启动压力梯度的概念及启动压力梯度存在的示意图（图1）。

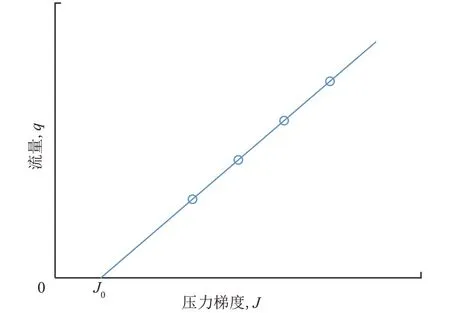
图1 Bear的压力梯度示意图[1]Fig.1 The sketch graph of q vs.J of Bear[1]

Bear由图1提出了如下的关系式：

当J=J0时，（1）式中的q=0；当J＞J0时，q＞0，即表明流体发生流动。

汪全林[5]发表的岩心测试资料（图2）表明，多数岩心并不具有启动压力梯度，而是通过原点的直线。

1.1 线性流的推导

对于均质、单相、稳定、恒温和层流的一维线性流动，Darcy（1856）根据实验建立的流量与压力梯度关系的微分式为：

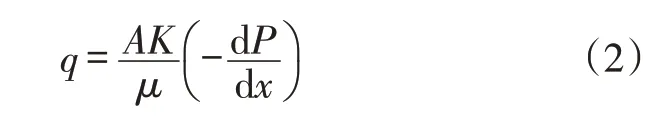
图2 流量与压力梯度的关系[5]Fig.2 Relation between q and ΔP/L[5]

（2）式中压力梯度前的负号表示压力沿流体流动的方向是下降的。对（2）式分离变量，代入积分上下限后为：

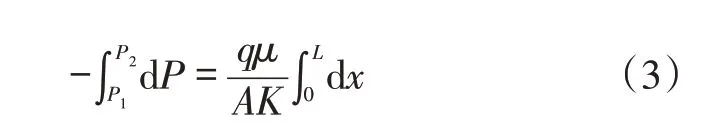
由（3）式积分后得达西的线性流压力梯度与流量的正比关系为：

其中：

对于同一个岩心，若进行多次流量测试（一般为4次），可以得到多个相应的压力梯度与流量数据。将这些数据点按（4）式关系绘于直角坐标系中，可以得到一条通过原点的直线。这表明该岩心不存在启动压力梯度。如果两者是一条具有截距的直线，则表示存在启动压力梯度（图3），而且直线的截距就是启动压力梯度。因此，当存在启动压力梯度时，由（4）式可得：

图3 线性流测试的ΔP/L与q的关系Fig.3 Relation between ΔP/L vs.q for the linear flow testing

由于线性流动的压力梯度和启动压力梯度均为常数，若将ΔP/L写为dP/dx时，（6）式又可写为：

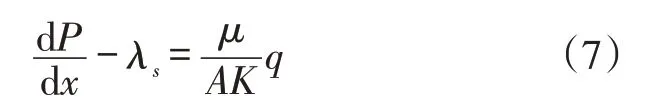
由于v=q/A，故（7）式可写为：

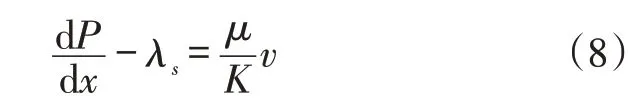
应该指出，线性流的上述推导，各项参数的单位均为SI 制基础单位，当改为岩心测试的室内实用单位（见符号注释）表示时，（4）式和（8）式分别为：

尽管，在理论分析上可以存在启动压力梯度λs，但正如图2所示，大多数岩心的测试资料并不能反映启动压力的存在。也就是说，个别低渗透岩心是存在启动压力梯度的。

1.2 平面径向流的反思与推导

对于均质、单相、恒温、稳定和层流的达西定律，在地层条件下，流量的微分式为：

已知平面径向流不同径向位置的渗流面积为：

将（12）式代入（11）式得平面径向流的压力梯度为：

由（13）式看出，平面径向流的压力梯度与径向半径r为反比的函数关系，随r数值的增加，压力梯度会显著的下降。现将（11）式改写为下式：

由（14）式看出，平面径向流的压力梯度与流速成正比。但应当指出，达西定律的这一正比关系，在低速流动时是正确的。然而，在高速流动条件下，就会偏离这一正比关系。Forccheimer（1901）通过实验与理论研究提出了如下的二项式模型：

在（15）式中a和b两个常数，分别称为达西流动常数和非达西流动常数[33-34]，a=μ/K和b=ρβ，这样（15）式可写为：

应当注意的是，对于平面径向流，（16）式等号右边的第1项为达西流动项，发生在远井地带；第2项为非达西流动项，发生在近井地带，因渗流面积的减小，流速的增加所引起的湍流影响。式中β为高速湍流系数，或惯性阻力系数，或Forccheimer系数。应当注意的是，由于平面径向流的压力梯度不是常数，而是径向半径r的函数，因此，其启动压力梯度也不是常数，而是径向半径r的函数。当以ηs（r）表示启动压力梯度时，由（16）式可得：

上述平面径向流的推导中各项参数的单位均为SI制基础单位。当改为矿场实用单位（见符号注释）表示时，（17）式可写为：

应当注意的是，由于在（18）式中非常数的ηs（r）的存在，该式是不能求解的。然而，对于高渗透性的油气井，并不存在启动压力梯度，即使对低渗透性的油气井，经过压裂，也不存在启动压力梯度。因此，在进行矿场产能测试时，均采用如下的二项式Quadractic Formula，求解油气井的绝对无阻流量和流入动态产能曲线（IPR）：

对于气藏，（19）式中气体在地层条件下的密度，由下式计算[35]：

在（19）式中的高速湍流系数，可由如下的相关经验公式确定[36]：

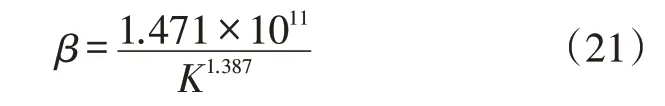
2.对压敏效应的反思与推导

所谓的压敏效应，是指地层渗透率随地层压力的下降而降低的现象。Fatt[2]于1952年利用室内岩心模拟实验研究结果得到了渗透率随上覆压力（Overburden Pressure）的增加而减小的现象（图4）。对此，后人称为压敏效应（Pressure Sensitivity）。在20世纪70年代美国岩心公司（Core Lab）提出用净上覆压力（Net Overburden Pressure）代替上覆压力，进行压敏效应的解释。我国的专家学者采用美国的方法，绘制压敏效应的关系图，但其实这样的做法是缺少理论依据的。因此，本文给出如下的推导。

图4 Fatt的KD与POB关系[2]（1 MPa=145.04 psi）Fig.4 Relation between KD and POB of Fatt[2]

图5为渗透率K随地层压力P的变化关系。

由图5可以看出，随着地层压力的下降渗透率是降低的。假设渗透率随压力的递减率采用Arps（1945）的定义为：

由于渗透率随压力的下降而降低，因此，（22）式中的dK/dP为正号。

将（22）式分离变量，代入积分上下限为：

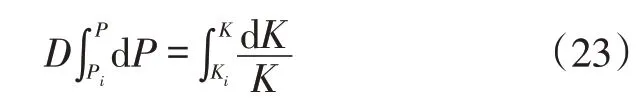
由（23）式积分可得下式：

由（24）式看出，渗透率K 与地层压力降ΔP 呈指数下降的关系。为了对压敏效应的渗透率与地层压降进行无因次分析，设无因次渗透率和无因次地层压力降分别为：

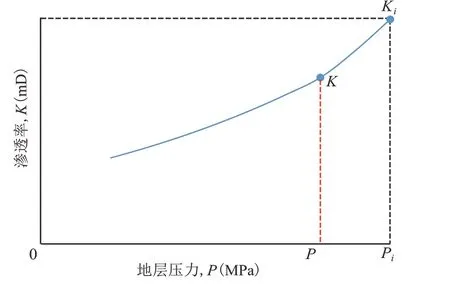
图5 K与P的关系Fig.5 Relation between K and P

将（25）式和（26）式代入（24）式得无因次压敏效应关系式为：

给予不同的ΔPD值，由（27）式求得的无因次压敏效应图（图6）。由图6看出，当ΔPD＞3时，压敏效应的影响很小。

图6 无因次压敏效应图Fig.6 Dimensionless pressure sensitivity effects

国外将净上覆压力定义为上覆压力与地层压力的差值，即：

由于POB为常数，对（28）式微分得：

将（29）式代入（22）式得：

对（30）式分离变量，代入积分上下限为：

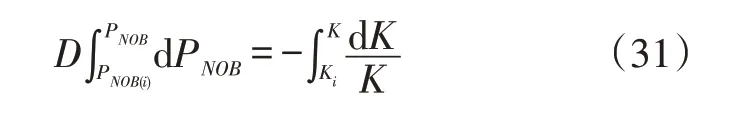
由（31）式积分可得，利用净上覆压力表示的压敏效应关系式为：

将（32）式改写为下式：

其中：

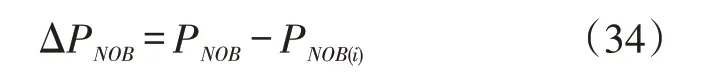
由（33）式看出，KD与ΔPNOB成指数下降关系，见图7。如果改为KD与PNOB作图，则在KD=1时，对应的PNOB≠0，而应等于PNOB（i）（图8）。在文献[13]中已清楚地看到这一问题的存在，如图9所示，因此，利用KD与PNOB作图是不正确的。

如果将压敏效应的渗透率下降关系，代入平面径向流达西微分式为：

图7 KD与ΔPNOB的关系Fig.7 Relation between KD and ΔPNOB

图8 KD与PNOB关系Fig.8 Relation between KD and PNOB

图9 KD与PNOB关系[13]Fig.9 Relation between KD and PNOB[13]

由于在（35）式中存在变量P，不但导致该式的无解，而且动摇了以常数渗透率为根基的达西定律。

3.结论

通过本文的理论研究，对于启动压力梯度和压敏效应可以得到如下的初步结论。

1）对于达西的线性流动，压力梯度和启动压力梯度都是常量。Bear（1972）基于一维岩心模拟实验研究，提出了启动压力梯度的概念，而且线性流的压力梯度与流量成正比的直线关系。通过原点的直线不存在启动压力梯度，当直线具有截距时，则存在启动压力梯度。并且直线的截距就是启动压力梯度。应当强调指出，启动压力梯度只存在于致密低渗油气藏。

2）对于平面径向流，压力梯度和启动压力梯度都不是常数，而是径向半径r的函数，因此，得不到像线性流那样表述启动压力梯度的方法。特别指出，绝不能将线性流的启动压力梯度，用于平面径向流方程，笔者曾就此发表过专文[37]。对于致密低渗透地层的油气井，由于没有自然产能，必须经过压裂才能投产。因此，在这种情况下，启动压力梯度已失去实际意义。目前在国外的文献中，均看不到有关启动压力梯度引用的内容。

3）国内外大量的室内岩心模拟实验结果表明，不同渗透率的岩心均存在压敏效应现象。通过本文的研究表明，压敏效应渗透率与地层压力降，或与净上覆压力降成指数的下降关系。在国内外的文献中常用的无因次渗透率KD与净上覆压力PNOB的作图方法是不正确的。这样做的结果表明，在KD=1时，PNOB≠0，而应当等于PNOB（i）。应强调指出，如果承认渗透率随压力而改变，那将会动摇达西定律建立的基础。

符号注释

（圆括号内为实用单位）

q—测试条件和地层条件的流量和产量，m3/s，（岩心cm3/min，矿场m3/d）；

A—渗流面积，m2，（岩心cm2，矿场m2）；

D—渗透率随压降的递减率，Pa-1，（MPa-1）；

h—厚度，m，（岩心cm）；

K—渗透率，m2，（mD）；

Ki—初始渗透率，m2，（mD）；

KD—无因次渗透率，frac，（frac）；

μ—岩心测试流体的黏度或地层流体黏度，Pa·s，（mPa·s）；

L—岩心长度，m，（岩心cm）；

r—径向半径，m，（m）；

x—线性流动距离，m，（岩心cm）；

P—压力或目前地层压力，Pa，（MPa）；

Pi—原始地层压力，Pa，（MPa）；

P1—岩心的入口压力，Pa，（MPa）；

P2—岩心的出口压力，Pa，（MPa）；

POB—上覆压力，Pa，（MPa）；

PNOB—P压力下的净上覆压力，Pa，（MPa）；

PNOB（i）—Pi压力下的净上覆压力，Pa，（MPa）；

ΔP—岩心的测试压差，Pa，（MPa）；

ΔPD—无因次压降，dim，（dim）；

ΔP/L—岩心的压力梯度，Pa/m，（岩心MPa/cm，矿场MPa/m）；

dP/dx—线性流的压力梯度，Pa/m，（矿场MPa/m）；

dP/dr—平面径向流的压力梯度，Pa/m，（矿场MPa/m）；

ΔPNOB—净上覆压力降，Pa，（MPa）；

J—Bear的压力梯度，Pa/m，（岩心MPa/cm，矿场MPa/m）；

J0—Bear的启动压力梯度，Pa/m，（岩心MPa/cm）；

λs—线性流的启动压力梯度，Pa/m，（岩心MPa/cm）；

ηs（r）—平面径向流的启动压力梯度，Pa/m，（MPa/m）；

v—渗流速度，m/s，（cm/s）；

ρ—流体密度，kg/m3，（g/cm3）；

ρg—地层气体密度，kg/m3，（g/cm3）；

γg—气体的相对密度，（dim）；

Z—气体偏差系数，（dim）；

T—气体绝对温度，K，（K）；

β—高速湍流系数，m-1，（m-1）。