惯性+星光折射定位组合导航技术研究

胡楠希，李小琥，李自行

(北京控制与电子技术研究所，北京 100038)

0 引言

由于现有惯性器件精度水平有限，纯惯性导航误差在千米级以上，因此需要采用组合导航的方式来提高导航精度。目前，全自主组合导航方式中传统的惯性+星光定姿组合导航方法只能实现定姿，不能实现定位，在精度上可提升空间有限。

星光折射自主导航技术是一种可进一步提高自主导航精度的有效途径[1-2]。美国对星光折射间接敏感地平自主导航的研究工作可以追溯到20世纪60年代[3-4]。近年来，国内高校和研究机构均开展了相关研究。文献[5]对利用星光折射间接敏感地平的自主导航的基本原理进行了介绍。文献[6-7]研究了大气折射原理及平流层大气变化规律。文献[8]利用现有大气密度模型和固定高度观测模型，建立了自适应星光折射模型。文献[9-16]对采用星光折射进行自主导航的方法进行了研究。

为此，提出了一种惯性+星光折射定位组合导航方法，重点从星光折射定位原理、大气折射模型、非线性滤波和选星策略几个方面进行论证及分析。通过理论分析与数学仿真相结合的手段，验证了星光折射定位原理的正确性及工程可行性，从而为进一步提高自主导航精度提供了一种技术途径。

1 惯性+星光折射定位组合导航原理

1.1 星光折射定位原理

星光折射定位导航方法是利用星光在大气中的折射角和折射高度之间的关系而间接敏感地平，从而实现高精度定位导航。

首先，星光在穿过大气层时会发生偏折。由于平流层(高度20～50km)大气密度比较稳定，使得视高度ha与折射角θss的关系可以用大气折射模型表示

ha=h0-Hln(θss)+

(1)

其次，视高度ha与观测点位置r、折射角θss之间存在如下几何关系

(2)

星光折射定位的几何关系如图1所示。

图1 星光折射定位几何关系图Fig.1 Geometric illustration of stellar atmospheric refraction positioning

综上所述，星光折射定位的基本原理如下：首先，通过星敏感器持续观测穿过平流层的多颗不同方向折射星，测量得到折射角；其次，根据大气折射模型与折射角计算得到视高度；最后，根据星敏感器测量得到的折射角与大气模型计算得到的视高度，建立惯性+星光折射定位观测方程，解算载体位置。该定位原理如图2所示。

图2 星光折射定位原理图Fig.2 Illustration of stellar refraction positioning

1.2 大气折射原理

公式给出的是简化的大气折射模型，是在假设大气密度与高度是指数关系，同时大气密度在全球均匀分布的前提下得到的。这个简化模型可以定性地说明大气折射的基本原理：折射角随着视高度的降低而增大。视高度与折射角近似关系如图3所示。

图3 视高度与折射角关系图Fig.3 Relationship between apparent height and refraction angle

从工程应用的角度看，简化的大气模型计算得到的视高度误差较大，因此需要构建考虑大气参数非均匀性的精确大气折射模型。

该方法得到的视高度与观测点位置、星光方向以及折射角有关，如式(3)所示

ha=f{Θ0,Φ0,Ψ,ni,hi|θss}

(3)

1.3 非线性滤波原理

常用的估计方法主要有两类：最小二乘法和Kalman滤波。最小二乘法比较适合对常值参数进行估计，而Kalman滤波适合对时变系统进行估计。传统的Kalman滤波算法需要对状态方程与观测方程进行线性化处理，对于线性系统有较好的适应性，但是随着滤波周期的增大以及系统非线性的增强，滤波的非线性误差也会增大。

无迹Kalman滤波(Unscented Kalman Filter，UKF)是一种针对非线性系统的滤波方法。对于线性系统来说,它的滤波性能与传统Kalman滤波相当;对于非线性系统,它的性能则明显优于传统Kalman滤波。在惯性+星光折射定位过程中，状态方程与观测方程既是时变的更是非线性的，因此通过上述分析可以得出，UKF算法是最适合惯性+星光折射的定位算法。

UKF算法不需要对系统进行线性化处理，其主要思想如下，假设一个离散非线性系统

xk+1=F(xk,uk,k)+ωkzk=H(xk,uk,k)+vk

(4)

(5)

标准的UKF算法如下：

初始化

(6)

计算采样点

(7)

状态方程更新

(8)

量测更新

(9)

式中，Qk和Rk分别为系统和量测噪声协方差。当xk为高斯分布时，通常选取n+τ=3。

从滤波算法中可以看到，状态方程与观测方程都没有进行线性化处理，而是直接采用实际的方程进行计算。系统状态估计误差通过采样点进行描述，并通过估计观测量与实际观测量的偏差对系统状态估计与方差进行修正。采样点示意图如图4所示。

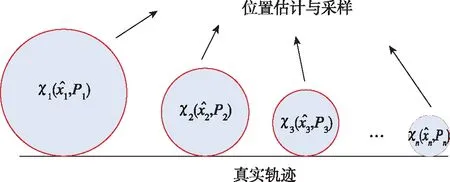
图4 采样点示意图Fig.4 Illustration of sample point

图4中，每一个圆代表每一次观测后估计的采样点分布，下方的横线代表真实轨迹。采样点的均值为每一次估计的位置，采样点的方差为估计的方差。由于初始位置误差较大，因此第1个圆会比较大，圆心距离真实轨迹较远。随着观测次数的增大，估计的方差会减小，估计的位置误差也会减小，因此圆会越来越小，最终收敛到真实的位置。

1.4 折射星分布原理

折射星的分布取决于观测点与星光方向的相对关系。如图1所示，定义地心矢量r与未折射的星光矢量s之间的夹角为α，则公式可以改写为

ha=|r|·sin(α)+|r|·cos(α)·tan(θss)-

Re(1+θss·tan(θss)/2)

(10)

由此可知，随着折射星视高度的增大，夹角α也在增大，可观测的折射星与观测点地心矢量的夹角为一个圆锥面，如图5所示。

图5 折射星分布示意图Fig.5 Distribution of refraction star

根据上述分析可知：在观测点移动过程中,持续观测同一颗折射星，地心矢量与星光矢量之间的夹角是在变化的，所观测到的折射角与视高度也是连续变化的。

2 惯性+星光折射定位组合导航的应用

2.1 基于非线性滤波的惯性+星光折射定位方法

为了将UKF算法应用于惯性+星光折射定位，需要对滤波方程进行细化，主要包括状态方程与观测方程。

滤波方程中使用的观测量为视高度，而直接的观测量是折射角，因此需要将折射角转化为视高度。通过采样点可以估计出相应的视高度估计值，这里需要用到视高度与位置的几何关系方程，该方程就是观测方程

(11)

通过直接观测量折射角还可以计算得到真实的视高度观测值，这里需要用到大气折射模型

ha=f{Θ0,Φ0,Ψ,ni,hi|θss}

(12)

基于方程的视高度估计值与视高度观测值之间的偏差对位置速度进行修正。从滤波开始，每一个滤波周期都进行状态方程的计算。当进行星光观测时，则进行量测的更新与状态的修正；当没有观测时，则只进行状态方程的计算。

滤波方程中，初始的位置取惯性导航的位置，初始的位置方差应设置为惯导误差的方差，量测噪声应选取折射角观测偏差引起的视高度偏差的方差。

滤波过程的示意图如图6所示。

图6 滤波过程示意图Fig.6 Illustration of filtering

2.2 折射星选星策略

折射星选星策略应包括2个部分：1)备选星的筛选；2)折射星的选择策略。

由于星库中的星较多，但是可用的折射星只是一小部分。另外，根据1.4节的分析可知，折射星的观测不仅需要关注观测的是哪一颗星，更要关注在什么时间去观测。因此，需要根据观测段的位置将所有可用的折射星筛选出来作为折射星备选星库，以便从中选择可用的折射星。

在已知折射星备选星库后，折射星的选择应该服从如下原则：1)选择不少于3颗星；2)所选星在方位上尽量分布均匀；3)前后2颗折射星的观测时刻间隔应该考虑调姿时间与连续观测时间。

3 数学仿真

在考虑了大气折射模型后，星光折射定位的算法流程如图7所示。

图7 惯性+天文组合导航工作流程图Fig.7 Workflow of inertial/stellar integrated navigation

大气折射模型根据输入的辅助数据与折射角测量值计算出该时刻的视高度，组合导航根据大气折射模型计算的视高度与星敏感器观测到的折射角进行星光折射定位。按照上述流程进行蒙特卡罗仿真。

仿真后统计的位置估计误差如表1所示。

表1 位置估计误差统计(3σ)

从仿真结果可以得出，基于非线性滤波的定位方法可以有效地消除观测误差并得到较高的位置估计精度，证明了惯性+星光折射定位算法合理有效。

4 结论

本文提出了一种惯性+星光折射定位组合导航方法，重点从星光折射定位原理、大气折射模型、非线性滤波和选星策略几个方面进行论证及分析。通过理论分析与数学仿真相结合的手段，验证了星光折射定位原理的正确性及工程可行性。采用该方法可以提高组合导航精度,从而为进一步提高自主导航精度提供了一种技术途径。