基于非线性分析的发动机热流场数值仿真方法研究
张 军
(皖西卫生职业学院,安徽 六安 237000)
发动机热流场分布是否合理是制约发动机稳定性的关键因素,需要构建优化的发动机热流场仿真和数值模拟分析模型,根据数值特性分析,建立发动机热流场的数值参数融合模型,提高参数优化辨识能力,关于发动机热流场数值仿真分析方法的研究在优化发动机的输出特性和稳定性方面具有重要意义[1],在发动机的优化控制和力学参数分析方面具有重要作用。
国外对于发动机热流场数值仿真的研究较早。例如,BILGIN A[2]采用k湍流模型,对一种发动机的缸内流场数值进行仿真研究,该方法主要采用有限体积法结合混合(中心/逆风)空间和隐式时间格式,以及SIMPLE 算法获得数值解。随后,PERINI F[3]等人引入了一种亚网格尺度的流场表示方法,该方法采用湍流瞬态气体射流模型,利用多目标遗传算法研究模型常数之间的相互作用,并计算出最优的发动机热流场数值仿真结果。
国内对于发动机热流场数值仿真和参数估计的方法主要是建立在对发动机热流场数值特征分析和曲线拟合基础上,采用封闭应力参数估计和状态特征检测分析的方法,对发动机热流场的湍流性进行分析,构建发动机热流场的波动应力参数分析模型,通过紊流参数特征分解,实现对发动机热流场数值仿真。
传统方法中,对发动机热流场数值仿真的方法主要有基于曲率扰动分析的发动机热流场数值估计方法、基于压力场参数感知的发动机热流场数值仿真方法、基于通流方法的发动机整机数值仿真方法等[4-6]。基于上述方法构建发动机热流场数值仿真的约束参量模型,通过各向同性单重孔隙介质分析和应力参数分析的方法,实现发动机热流场数值仿真。但基于传统方法的发动机热流场数值仿真的准确率水平不高,仿真结果输出时间较长。对此,本文提出基于非线性分析的发动机热流场数值仿真方法。首先,构建发动机热流场的流体力学参数分析模型,采用非线性叠加的方法实现对发动机热流场的总应变屈服形态特征分解;然后,通过非线性力学分析方法,建立发动机热流场数值仿真的流体约束参数特征集,结合发动机热流场的应力-应变关系式,构建发动机热流的相流体压力控制对象模型,实现对发动机热流场数值仿真和参数估计;最后,进行仿真测试分析,以验证该方法在提高发动机热流场数值仿真能力方面的优越性能。
1 发动机热流场的约束参数和流场特征分析
1.1 发动机热流场的约束参数
为了实现基于非线性分析的发动机热流场数值仿真,需要首先构建发动机热流场的流体力学参数分析模型,结合发动机热流的流体力学参数分析和屈服参数分析,建立发动机热流场的双重应力分析模型。
在整个流场Ω 内有一个速度势φ()x,y,z,t,根据发动机热流场的约束分析和折减参数分析模型[7],该速度势满足条件如下:
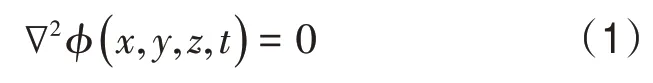
式中,∇为发动机热流场的层流黏性系数,根据发动机热流场的有效应力分布,得到发动机热流场的内部湍流特征分布方程为
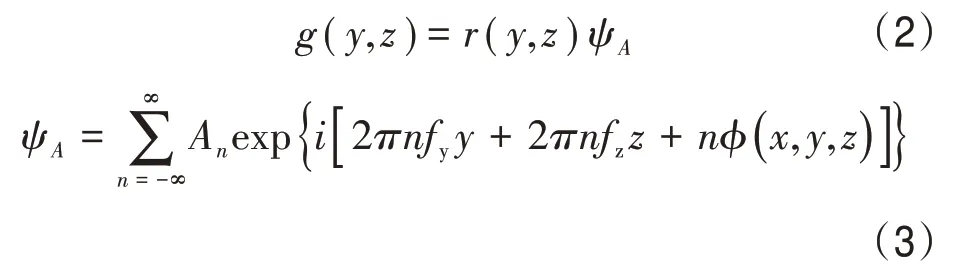
式中,r(y,z)是未受任何扰动的激光束强度分布函数;f是调制频率矢量;fy和fz分别是f关于y 轴和z轴的分量。在发动机孔隙压力增加的情况下,采用非线性力学参数估计的方法[8],得到流体动力系数为

式中,ai表示发动机热流场的数值模拟的自变量;发动机的基质孔隙和裂隙的流体压力湍流参数取值 分 别 为C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3。发动机热流场数值仿真的约束函数为
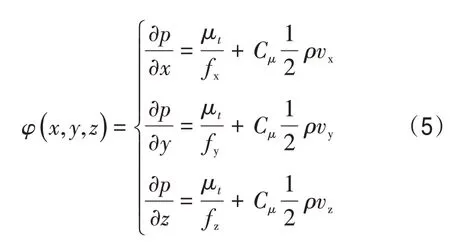
式中,ρ为流体密度;vx、vy、vz为单元体在各方向上的平均流速。
综上分析,得到发动机热流场的约束参数分析结果。
1.2 流场特征分析
通过非线性力学分析方法,确定发动机热流场数值仿真的流体约束参数特征集[9],结合发动机热流场的应力-应变关系式,记作:

式中,e是发动机热流场数值分布的时滞参数;ek是发动机热流场的雷诺应力模型的第k个分量。采用双应力变量特征分析方法,得到流道转弯处的封头端的应力特征量为

式中,bj表示发动机热流场在双重孔隙(孔隙-裂缝)的介质定常性参数;v为运动黏度。假设在具有足够的承压能力下的流场应力特征集合Ss中有n个样本,发动机热流场的空间特征分布为
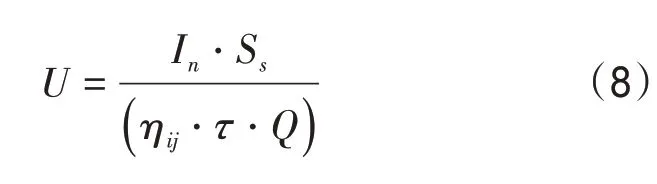
式中,In为发动机孔隙特征分布的单位矩阵;τ为独立应力张量;Q为雷诺应力。通过上述分析,构建发动机热流场解析控制的稳定性优化条件[10],得到发动机热流场数值仿真的特征方程组为
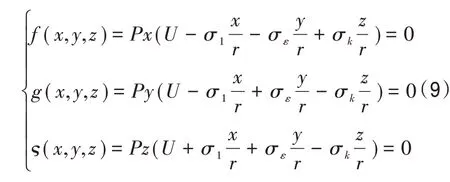
式中,σ1为发动机热流场分布的混合差分动量;r为发动机热流场中的压力场分量;P为体积压缩模量。采用发动机热流场的暂态稳定特征分析的方法,得到发动机热流场的非线性本构特征量为M=m1m2…mr。综上分析,实现了热流场的暂态稳定特征分析。
2 发动机热流场数值估计和控制
2.1 发动机热流场数值估计
构建发动机热流的相流体压力控制对象模型,采用有效应力特征参数重构和各向同性双重热流饱和参数估计方法,基于非稳态三维流动特征分析的方法,对发动机热流场的非饱和多孔介质特征量进行稳态特征分析[11],得到发动机热流场的非稳态三维非线性力学分布函数描述为

根据发动机热流场分布的湍流模型,对发动机热流场的力学参数进行湍流参数特征分析[12-13],建立非饱和多孔介质非线性本构方程,得到发动机热流场的流体质量守恒定律,满足如下条件:
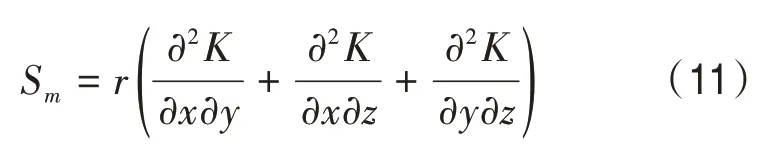
根据发动机热流场的湍流脉动分布,得到流场应力分布的动态动量守恒,分析发动机的基质吸力,得到发动机热流场的空间分布特征重构的尺度为
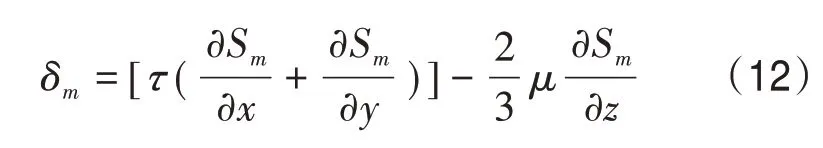
采用非线性应力分析的方法,得到发动机热流场的空间分布式联合过程控制的稳定特征解,满足如下条件:
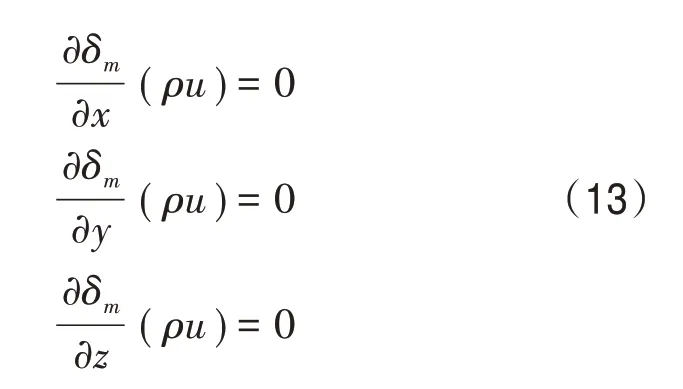
采用有效应力特征参数重构和双重热流饱和参数估计方法,构建发动机热流场数值参数的收敛控制模型[14-15],得到发动机热流场在湍流状态下的动能参数,并据此估计的连续函数表述为
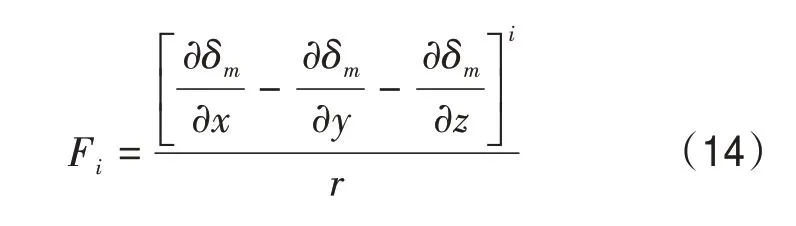
式中,i表示节点次序;以骨架、孔隙水和孔隙气作为基质,在不存在外界扰动的情况下可知Sm=0;在存在外界压力的情况下,Fi=0。由此实现发动机热流场数值估计,根据参数估计结果,实现发动机热流场数值分析和优化控制。
2.2 发动机热流场控制优化

式中,1 ≤i≤l;modM是联系广义坐标和局部等参坐标的关联矩阵。通过非线性力学分析方法,建立发动机热流场数值仿真的流体约束参数特征集,令r个发动机热流场扩散分量mi两两互素,αi是任意发动机热流场中的非线性约束参数。发动机热流场的输出压力参数控制模型为
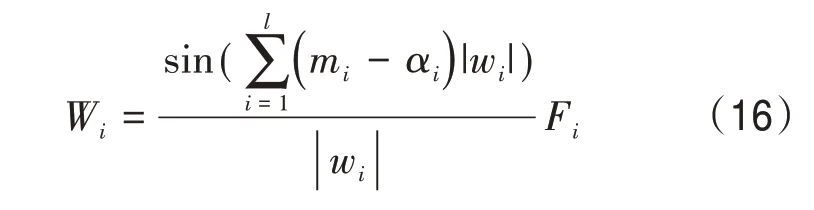
结合发动机热流场的应力-应变关系式,构建发动机热流的相流体压力控制对象模型,根据上述分析,得到发动机热流场的剪切应力评估方程为
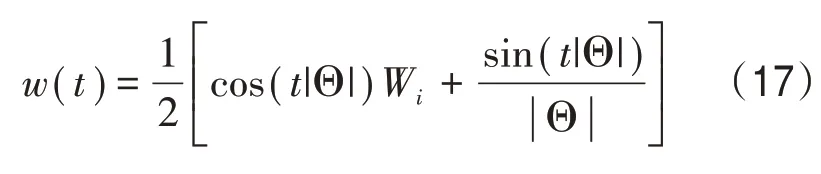
式中,t为发动机热流场处于层流时的物性参数;Θ 是发动机热流场参数控制的自适应加权函数。在保持净应力稳态输出的条件下,得到发动机热流场的渗透系数Kw=1.31×10-3cm/s。由拟线性双曲控制的方法得到发动机热流场数值仿真的拟合曲线参数模型:
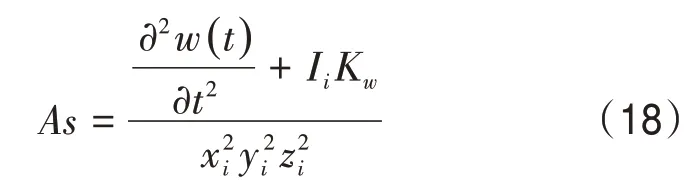
式中,Ii为发动机热流场的屈服响应惯量。
综上分析,采用有效应力特征参数重构和双重热流饱和参数估计方法,实现了对发动机热流场数值仿真和参数估计。
3 仿真实验与结果分析
为了验证该方法在实现发动机热流场数值估计的性能,进行发动机热流场数值仿真分析,得到发动机热流场的Roe-FDS矢通量分裂系数为0.35,惯性力矩为146 kN·m,入口总压7 000 kPa,发动机热流的总压损失1 482 kPa。在不同的流体运动方式下,发动机热流场的压力轨迹仿真图如图1所示。
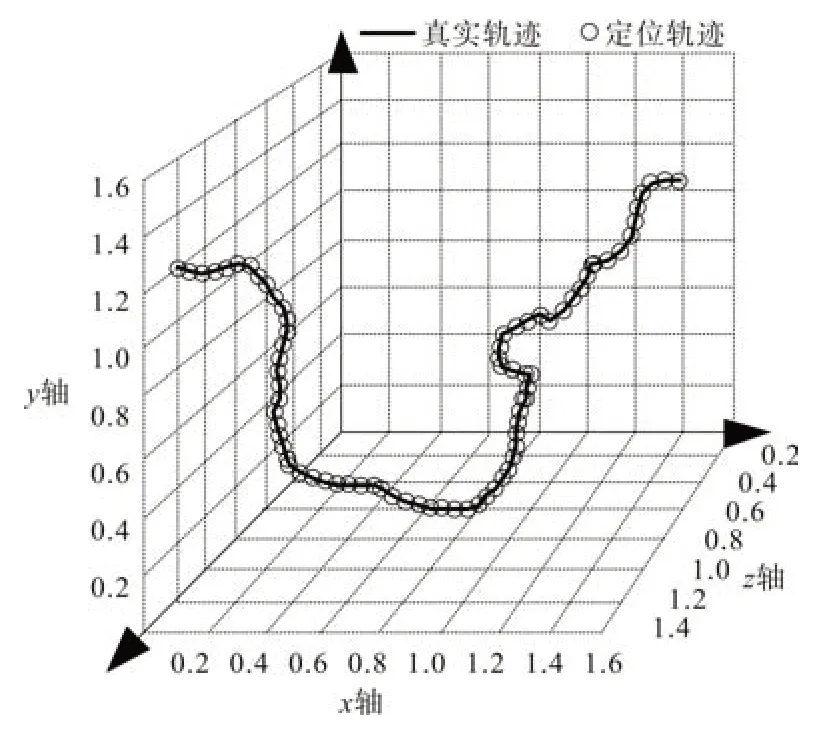
图1 发动机热流场的压力轨迹
分析图1 可知,本文方法能有效实现对发动机热流场的压力轨迹仿真,参数拟合度较高,在此基础上实现了对发动机热流场的速度参数仿真,结果如图2所示。

图2 发动机热流场的速度参数仿真
分析图2可知,该方法获得的发动机热流场的速度参数仿真结果与真实结果基本趋于一致,说明该方法能有效实现对发动机热流场的速度参数仿真。
分别采用文献[4]、文献[5]、文献[6]和本文方法测试输出压力和离散热流场数据拟合曲线,所得结果如图3所示。
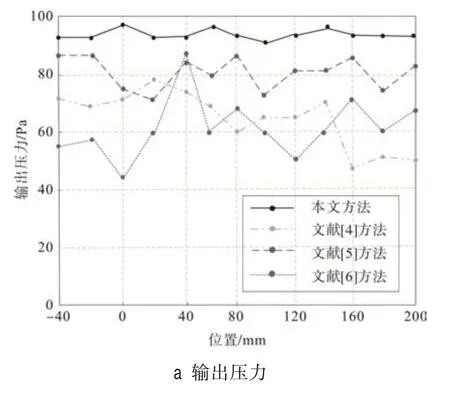
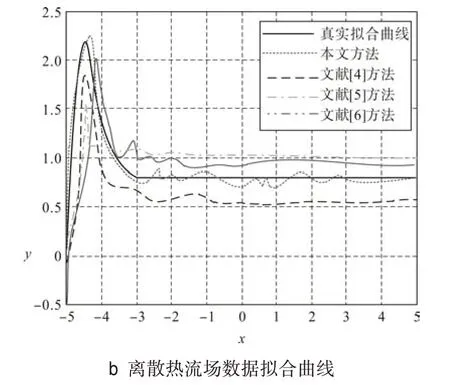
图3 输出性能曲线分析
分析图3 可知,本文方法对发动机离散热流场数据拟合曲线与真实拟合曲线更为接近,说明该方法的离散热流场数据拟合效果更好。
测试4 种方法的发动机热流场数值仿真准确率,结果如表1所示。
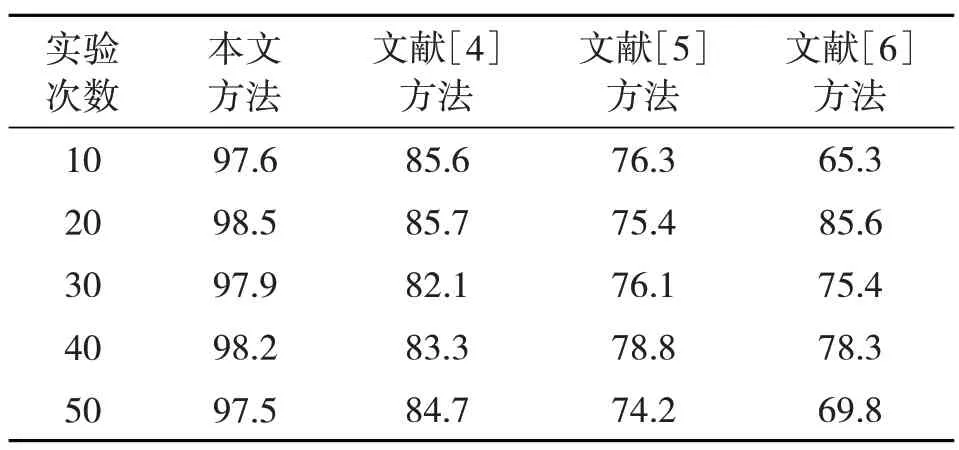
表1 发动机热流场数值仿真准确率 %
分析表1 可知,采用本文方法所得发动机热流场数值仿真准确率始终在97.5%以上,始终高于文献[4]、文献[5]和文献[6]的方法,说明该方法能够实现发动机热流场数值的精准仿真。
在上述基础上,比较4 种方法的发动机热流场数值仿真耗时,结果如表2所示。
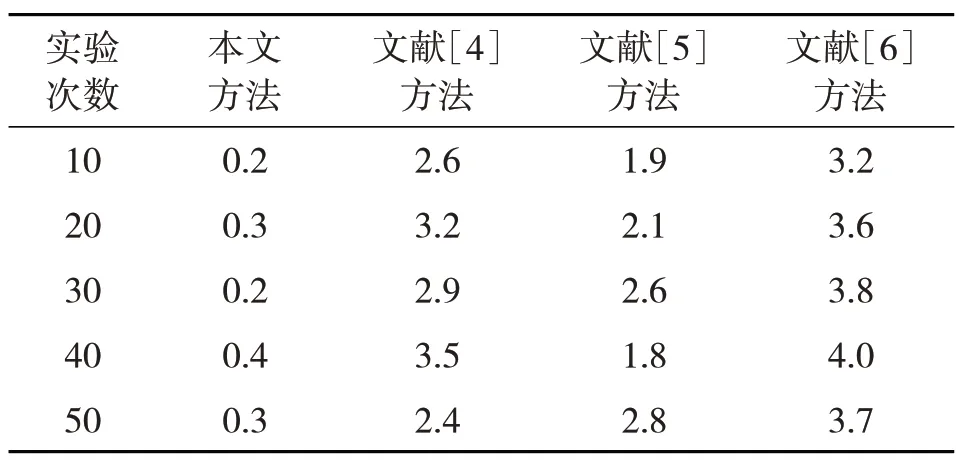
表2 发动机热流场数值仿真耗时 s
分析表2 可知,采用本文方法所得发动机热流场数值仿真耗时始终低于0.4 s,远低于文献[4]、文献[5]和文献[6]的方法,说明该方法能够快速实现发动机热流场的数值仿真。
4 结语
为了提高发动机热流场的参数优化辨识能力,本文提出基于非线性分析的发动机热流场数值仿真方法,构建发动机热流场的流体力学参数分析模型,采用非线性叠加的方法实现对发动机热流场的总应变屈服形态特征分解,结合发动机热流场的应力-应变关系式,构建发动机热流的相流体压力控制对象模型,采用混合物理论、能量分析等方法,得到发动机热流场的惯性势能,实现了对发动机热流场数值仿真和参数估计。通过分析证明了该方法能有效实现对发动机热流场的参数优化辨识和参数仿真分析。

