基于深度增强学习的海克斯棋博弈算法研究

郑博宇

北京信息科技大学 北京 100085

引言

海克斯棋，也称作六贯棋[1]，最初在丹麦报纸Politiken发表的一篇文章里出现，当时称Polygon。1948年，John Nash却又将其重新独立发明出来，而热衷于此的玩家们随即就将其称作Nash。稍后1952年Parker Brothers发行了一个版本，将其称为Hex，从此这个名字就固定了下来。六贯棋通常使10×10或11×11的菱形棋盘，而JohnNash 采用的却是14 × 14 的棋盘。

海克斯棋的规则如下：

（1）一共两人参与海克斯棋博弈，棋盘由红蓝两色组成。棋盘边缘分别填上双方颜色；

（2）双方轮流下棋，一次只能下一棋子，且仅占领一处空格，在空格上方放上属于自己颜色的棋子；

（3）在比赛的过程中，禁止吃棋子的行为；

（4）第一个把棋盘两端属于自己颜色的棋盘边缘连通成一条线的人获胜。

1 深度强化学习的算法模型设计

深度强化学习Deep Q-Learning是将Q Learning与CNN卷积神经网络相结合，实现了从感知到动作的端到端的革命性算法。普通的Q-learning算法中，当项目的状态和动作空间是离散且维数不高时可使用Q-Table储存每个状态动作对的Q值，但是在海克斯棋的博弈过程中，13×13的棋盘状态和动作空间是高维连续时，使用Q-Table过于庞大，建立起来十分困难。本文将海克斯棋类博弈与Deep Q-learning深度增强学习算法结合起来，使得该棋类的博弈能力不断提升。

1.1 Q learning 算法的结构

Q Learning是一种在强化学习算法中基于value-based的算法。Q即为Q（s,a），Q（s,a）在某一时刻的 s 状态下(s∈S)，采取 动作a (a∈A)动作能够获得收益的期望，通过Q值进行学习，而环境将会根据agent的动作反馈相应的回报reward r，所以本算法的主要思想是将State与Action构建成一张Q-table来存储Q值，再根据Q值来选取能够获得最大的收益的动作。Dlearning的更新方式，推导函数如下：

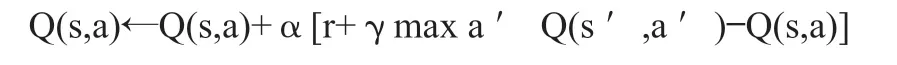
上式更新公式，根据下一个状态s’中选取最大的 Q ( s ′, a ′ )， Q(s’,a’)值乘以衰变γ加上真实回报值最为Q现实，而根据过往Q表里面的Q(s,a)作为Q估计。

1.2 深度增强学习的算法流程设计

为了使得算法性能更稳定，DQN中存在两个结构完全相同但是参数却不同的网络，一直在更新神经网络参数的预测Q估计的网络MainNet和参数固定不动预测Q现实的神经网络TargetNet。Q ( s , a ; θ i ) Q(s,a;θ_i) Q(s,a;θ i)表示当前网络MainNet的输出，用来评估当前状态动作对的值函数；Q(s,a;θi−) Q(s,a;θ^−_i) Q(s,a;θi−) 表示TargetNet的输出，可以解出targetQ，初始时刻将MainNet的参数赋值给TargetNet，然后MainNet继续更新神经网络参数，而TargetNet的参数固定不动。再过一段时间将MainNet的参数赋给TargetNet，如此循环往复。这样使得一段时间内的目标Q值是稳定不变的，从而使得算法更新更加稳定。

2 界面以及算法的实现

2.1 界面实现

根据海克斯棋棋谱[3]，本棋的棋盘是一个由11×11个六边形组成的棋盘。具体界面如图2所示。根据海克斯棋的规则和特点，使用PyQt5实现海克斯棋人机博弈软件。棋盘由11×11个六边形棋格组成，坐标原点在最下面正中间，坐标分别从11到1，从K到A。该软件具备区分先手后手，输出棋谱、悔棋等博弈基本功能。

2.2 卷积神经网络实现

博弈项目采用Theano构建和训练卷积神经网络。网络架构来自于谷歌DeepMind在AlphaGo中采用的架构网络结构，该结构由十个卷积层和一个完全连接的输出层组成。

过滤器使用六边形以更好地观察棋局的局部性。通过对方形滤波器应用Theano的卷积运算，即可生成六角滤波器。每个卷积层共有128个过滤器，由直径3和直径5六角形组成。每个卷积层的输出是简单的直径5和直径3的填充输出。输出使用sigmoid函数，其余所有的激活函数都是ReLU。网络的输出对应相应位置的动作价值的矢量。且网络依旧会评估不可移动和棋子已经下过的位置。

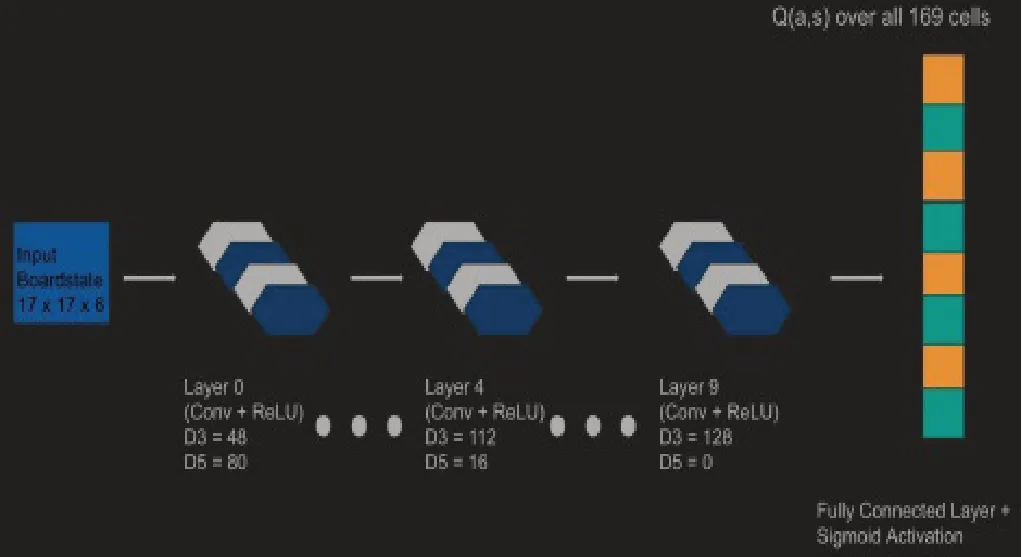
图3 卷积神经网络图

其中D3表示直径为3的滤波器的数量，D5表示所示图层中直径为5的滤波器的数量。

2.3 深度强化学习算法的实现

初始化replay memory M, Q-network Q,和状态D，执行相应的博弈次数，S为从D开始的位置，根据先手后手下棋。当棋局没有结束，a = epsilon greedy policy(s, Q)，snext = s.play(a)，如果游戏结束则r=1，没结束r=0。M.add entry((s,a,r,snext))，(st,at,rt+1,st+1) = M.sample batch() ，targett = rt+1 − max a Q(st+1)[a]。对Q执行梯度下降步降低(Q(st)[at]− targett)2, s = s.play(a)。在海克斯棋项目中，深度增强学习采用greedy policy(s, Q)的策略算法，直接采取具有最大Q值的动作作为当前策略，小部分时间采取随机动作用于探索。同时，使用RMSProp作为梯度下降的办法。

图4 DQN伪代码

3 实验结果及其分析

本文将基于Deep Q-learning深度增强学习算法的海克斯棋程序与基于UCT的海克斯棋程序进行博弈。一共测试五十局，分别先手比二十五局，后手比二十五局。

经过博弈结果，可发现基于深度增强学习算法的海克斯棋程序胜率很大，证实了基于深度增强学习算法改进的有效性。在一定程度上增加了找到最优落子坐标的概率，从而大幅提升了算法效率。

4 结束语

本文将深度增强学习和海克斯棋的博弈相结合并开展相应研究。深度强化学习算法组成部分的算法与相应公式，包括Q learning算法，AlphaGo和卷积神经网络结构等。实验结果表明，结合了深度强化学习算法的海克斯棋可以通过不断的训练与博弈，提升博弈的能力。