基于相似日理论和LIBSVM软件中SVR算法的光伏发电系统输出功率预测方法

吴诗芹，陆豪乾

(1．江苏林洋新能源科技有限公司林洋新能源研究院，南京 210004；2．江苏林洋光伏运维有限公司，南京 210004)

0 引言

太阳辐射能是光伏发电系统的唯一能量来源。由于受到昼夜交替、季节更迭、天气变化、地理位置等因素的影响，导致光伏发电具有间歇性、随机性、波动性的特点。因此，准确预测并网型光伏发电系统的输出功率，对电网调度，以及电网的安全稳定和经济高效运行具有重要意义。

目前已有许多预测并网型光伏发电系统输出功率的方法，并以各类神经网络算法及将神经网络算法与粒子群算法、遗传算法等相结合的算法为主[1-2]。而且由于神经网络算法的学习能力与泛化能力较强，该算法得到了更为广泛的应用[3]。

文献[4]提出了一种基于Elman神经网络模型的光伏发电系统输出功率的短期预测方法。结果显示，晴天条件下，该模型的预测精度较高；但在阴雨天气条件下，该模型的预测结果不理想。文献[5]提出了通过提高气象数据的聚类效果来提高训练集与待预测日的相关度，从而提升光伏发电系统输出功率短期预测精度的方法。但由于气象数据维度较多，很难采集到所有维度的气象数据，导致相关度的提高受到限制。文献[6]基于思维进化算法和反向传播(BP)神经网络算法建立了一种光伏发电系统输出功率的短期预测模型，提高了BP神经网络算法的预测精度。但BP神经网络算法易出现局部最优和迭代收敛慢的问题。文献[7]提出了通过对不同时刻气象因子赋予不同的影响权重来改进相似样本的输出选取与特征提取，从而进行光伏发电系统的功率预测。但由于此方法需要对不同时刻的气象因子赋予不同的权重，存在聚类过程较为复杂、计算量太大的缺点。文献[8-9]提出了小波分析和神经网络相结合的预测方法，降低了神经网络模型的预测误差，更适合光伏发电系统输出功率的超短期预测。文献[10]建立了基于遗传算法-模糊径向基神经网络算法的预测模型，但该模型中相似日的选取过于简单，未考虑空气相对湿度等气象因素对光伏发电系统输出功率的影响。

为进一步提高光伏发电系统输出功率的预测精度，本文提出了一种基于相似日理论和LIBSVM软件中支持向量机回归(SVR)算法的光伏发电系统输出功率预测方法，并与同样采用相似日理论的反向传播(BP)神经网络算法、径向基(RBF)神经网络算法和Elman神经网络算法的仿真结果进行了比较分析，对本文所提出的预测方法的有效性进行了验证。

1 相似日理论及其提取方法[11-12]

1.1 相似日理论

众所周知，太阳辐射能是光伏发电系统输出功率的唯一能量来源。而研究发现，影响光伏发电系统输出功率的因素很多，其中气象因素包括太阳辐照度、大气温度和相对湿度、风速及气压等。不同的季节、天气类型或地理位置，均会导致光伏发电系统的输出功率不同。

相似日理论的基本原理是：对于气象特征参数相似的日期，这些日期的光伏发电系统输出功率曲线也会近似相同。因此，选择一个与待预测日具有相似气象数据的日期作为相似日，将相似日的光伏发电系统输出功率作为参考值，可以得到待预测日的光伏发电系统输出功率。

1.2 相似日的提取方法

1)按春季(3～5月)、夏季(6～8月)、秋季(9～11月)、冬季(12～次年2月)4个季节的时间序列将光伏发电系统的输出功率及与其相关的气象数据分为4个样本集；然后再根据太阳辐照度、大气温度和相对湿度这3个气象因素，采用聚类方法将各个样本集内的数据分为晴天、多云、阴天、雨(雪)天等几个样本子集。

2)由于在实际工程中，风速、气压等物理量的采集数据严重缺失，但这些数据不是影响光伏发电系统输出功率的主要因素，因而本文将太阳辐照度、大气温度和相对湿度作为相似日提取时的输入参数。根据数值天气预报提供的待预测日的气象数据，在上述样本子集中找出3～5个与待预测日具有相似气象数据的日期。

3)将相似日的气象数据输入LIBSVM软件中的SVR模型，并进行训练。

在光伏发电系统的实测数据中会存在少量数据缺失的情况，可以通过线性插值的方法补全缺失值；对春季、夏季、秋季、冬季4个样本集中的离群值，可以通过与该值临近的实测值进行补正。同时，由于太阳辐照度、大气温度及相对湿度等物理量的量纲不同，取值范围不等，因此需要先对太阳辐照度、大气温度、相对湿度等数据进行归一化处理，然后再用聚类算法提取相似日。

2 基于LIBSVM软件中SVR算法的预测[13-14]

LIBSVM软件是由中国台湾大学林智仁教授等开发设计的一款简单、易于使用和快速有效进行支持向量机(SVM)模式识别与回归的软件包，该软件可用于解决分类和回归等诸多问题。

本文案例采用LIBSVM软件中的SVR算法，SVR算法是指利用SVM逼近函数的方法。

SVR算法为：给定一个数据序列｛xi,yi｝∈ (x,y)，其中i=1, 2, …,n。n表示总的训练样本个数，x是xi的集合，y是yi的集合。其中，x为影响光伏发电系统输出功率的因素，包括太阳辐照度、大气温度、相对湿度、风速等；xi为n个影响因素样本中的第i个样本；y为光伏发电系统输出功率；yi为n个输出功率样本中的第i个样本。

基于光伏发电系统运行历史数据库，提取出系统采集到的太阳辐照度、大气温度、相对湿度及光伏发电系统输出功率等历史数据。根据SVR算法，建立光伏发电系统输出功率预测模型，即寻找影响输出功率的因素与输出功率之间的关系，回归函数的公式为：

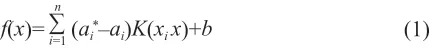
支持向量机的本质是基于核函数的方法，核函数的选择会直接影响到分类结果的准确性。常用的核函数包括：1)RBF核函数，比如K(xi x)=exp(-||x–xi||2/σ2)，其中σ是宽度系数。2)线性核函数，比如，K(xi x)=xi x。3)多项式核函数，比如K(xi x)=(xi x+1)d，其中d为多项式的次数，默认值为3。4)Sigmoid核函数，比如K(xi x)=tanh[γ(xi x)+θ]，其中γ的默认值为1/k，k为类别数；θ用来设置核函数中的coef0，默认值为零。上述常用的核函数中，RBF核函数的运算复杂度相对较低，因此本文选用RBF核函数[15-18]。

对于模型参数如何选择，目前尚无统一的理论方法，一般是结合具体问题，凭借经验或通过反复试验确定相关参数[16,19]。采用LIBSVM软件中的SVR算法进行计算时，需要设置nu、v和ε等参数，其中，nu的不同取值分别表示设置不同的计算模式；v表示交叉验证模式，v值必须大于2；ε表示终止阈值。对于本文的算例，通过验算比较，最终选择的参数是nu=0.5，v=5(表示5折交叉验证)，允许的终止阈值ε=0.0001。

3 预测结果与分析

本文以江苏省某光伏电站的实测数据为例进行仿真计算。测试时间为2018年12月～2019年11月，每天07:00～17:00，每隔15 min采集1组数据，采集内容包括太阳辐照度、大气温度、相对湿度和光伏发电系统的输出功率。由于7月受国家电网安全大检查的影响，导致部分数据未能上传，存在数据缺失；此外，由于少数日期采集到的样本数据缺失太多，所以这些日期的样本数据直接舍弃。因此，采集数据实际的有效天数为334天，每天采集41组数据，每组数据包括太阳辐照度、大气温度、相对湿度、光伏发电系统输出功率这4个气象参数，共计54776个样本数据。

为了验证本文所提预测方法的有效性，在每个季节不同天气类型的每个样本子集中各选择3个日期作为待预测日的相似日，组成测试集。将测试集中每个日期的太阳辐照度、大气温度及相对湿度作为输入参数，分别采用SVR算法、RBF神经网络算法、BP神经网络算法及Elman神经网络算法预测光伏发电系统的输出功率，并将预测值与实际的光伏发电系统输出功率(实际值)进行对比。

春季、夏季、秋季、冬季这4个季节不同天气类型时利用不同算法预测的光伏发电系统输出功率曲线，以及实际的光伏发电系统输出功率曲线情况，分别如图1～ 图4所示。

由于采用BP神经网络算法和Elman神经网络算法时，二者初始化时的权值和阈值是随机的，因而采用这2种算法进行预测时，每次预测的结果会不一样。

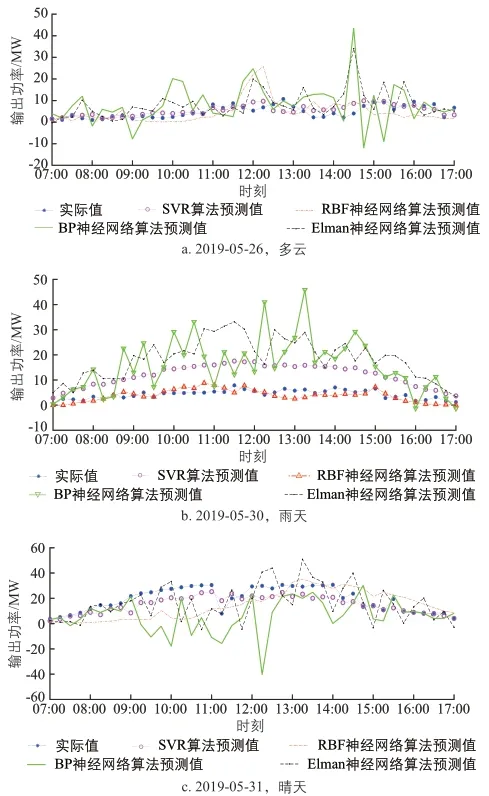
图1 春季不同天气类型时各种算法的光伏发电系统输出功率预测值与实际值曲线Fig. 1 Curves of predicted output power and actual output power of PV power generation system of various algorithms in different weather types in spring

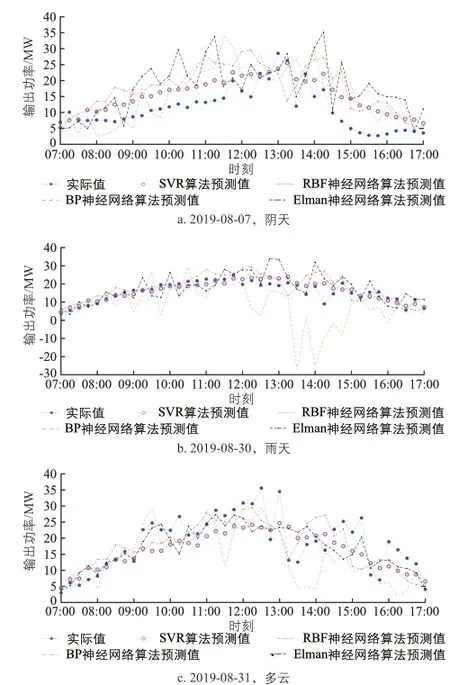
图2 夏季不同天气类型时各种算法的光伏发电系统输出功率预测值与实际值曲线Fig. 2 Curves of predicted output power and actual output power of PV power generation system of various algorithms in different weather types in summer

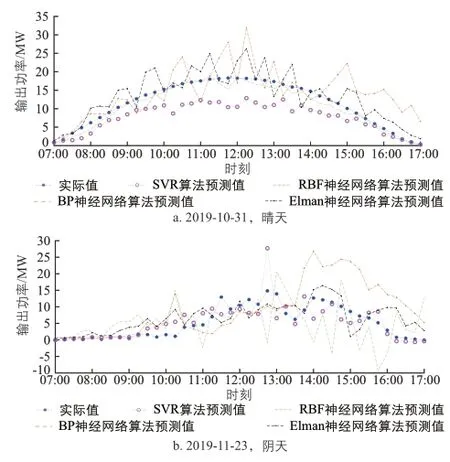
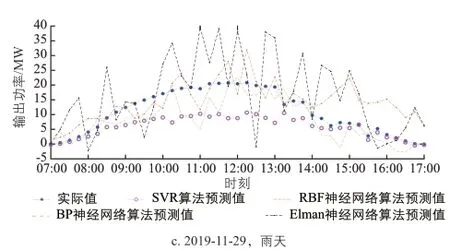
图3 秋季不同天气类型时各种算法的光伏发电系统输出功率预测值与实际值曲线Fig. 3 Curves of predicted output power and actual output power of PV power generation system of various algorithms in different weather types in autumn

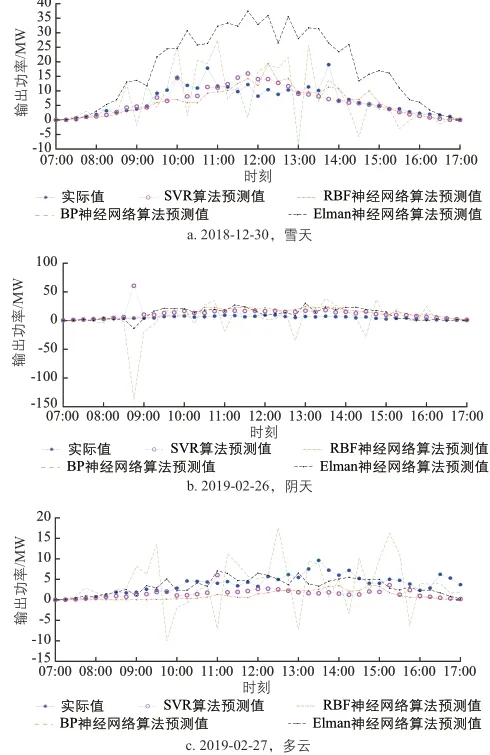
图4 冬季不同天气类型时各种算法的光伏发电系统输出功率预测值与实际值曲线Fig. 4 Curves of predicted output power and actual output power of PV power generation system of various algorithms in different weather types in winter

由图1～图4可知，采用LIBSVM软件中SVR算法预测的光伏发电系统输出功率曲线与实际的光伏发电系统输出功率曲线最为接近。

本文采用均方误差MSE作为评价预测结果的标准，MSE值越小，表明预测的准确度越高。

表1为分别采用4种预测方法时得到的MSE值。

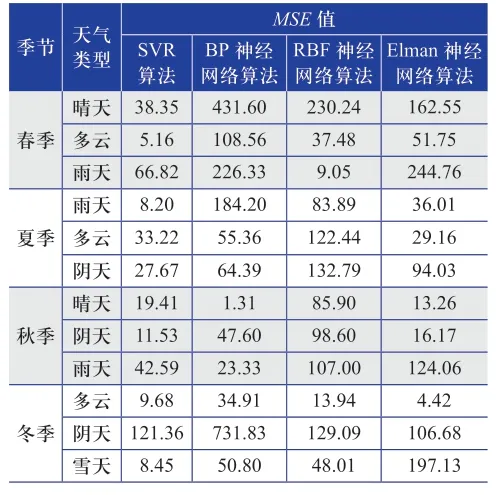
表1 4种预测方法得到的MSE值Tabel 1 MSE value obtained by four predicted methods

从表1中可以看出，采用SVR算法预测光伏发电系统输出功率时得到的MSE值明显低于采用其他3种预测方法时得到的MSE值，这说明SVR算法的预测准确度最高。

仿真计算过程显示，由于采用BP神经网络算法和Elman神经网络算法时引入了随机数，因此采用这2种算法时每次的预测结果均不一样。而采用SVR算法不仅预测结果明显优于其他2种算法，且每次的预测结果均一致。

用于模型训练的样本数量及其与待预测日的相似程度对预测结果有显著影响，样本数量越多，预测结果就越准确；样本与待预测日的相似度越高，预测结果也越准确。

4 结论

针对提高并网型光伏发电系统输出功率预测的准确性，有助于电网的安全稳定和经济高效运行，本文提出了一种基于LIBSVM软件中SVR算法的光伏发电系统输出功率预测方法，并与同样采用相似日理论的BP神经网络算法、RBF神经网络算法和Elman神经网络算法的仿真结果进行了比较分析，得出以下结论：

1)采用SVR算法时得到的MSE值明显低于采用BP神经网络算法、RBF神经网络算法及Elman神经网络算法时得到MSE值，这说明SVR算法的准确度最高；

2) 用于模型训练的样本数量及其与待预测日的相似程度对预测结果有显著影响，样本数量越多，预测结果就越准确；样本与待预测日相似度越高，预测结果也越准确。