基于非线性时变SEIR模型的新型冠状病毒肺炎传播机制

程万港，陈万铭，陈烨丽，夏志乐

（台州学院 电子与信息工程学院，浙江 临海 317000）

0 引言

新型冠状病毒肺炎（以下简称新冠肺炎）是由2019新型冠状病毒所感染导致的肺炎，经常伴有发热、干咳、乏力等症状。因此，它的临床症状与普通肺炎以及普通感冒极其相似。但新冠肺炎与普通流感不同的是，其对人体有极大的危害性。由于新冠肺炎起病隐匿，潜伏时间是时变不确定的，一般为1～14天。早期容易与感冒以及普通肺炎混淆，极易导致漏诊或误诊乃至死亡，而且它具有极强的传播性。自疫情暴发以来，截至2020年7月24日，全球累计确诊新冠肺炎病例15，641，288例，治愈926，505例，累计死亡635，598例。目前，虽然中国疫情得到了很大程度的控制，但国外感染人数仍在持续增加，严重影响人类的健康和世界经济的发展。因此对新冠病毒的传染机理和调控措施的研究显得尤为迫切。

目前已有众多的学者致力于新冠肺炎疫情预测及防控的研究，建立了相应的新冠肺炎数学模型，为新冠肺炎的调控起到了积极的作用。Qun等［1］搜集了肺炎人口统计学特征等信息，估计了疫情倍增时间和基本生殖数；Wan等［2］研究了武汉封城数据，基于SEIR建模方法，预测了武汉市疫情感染人数峰值；Joseph等［3］预测了新冠肺炎在国内以及全世界范围内的公共卫生风险和药物预防干预措施；Smirnova等［4］比较了正则化算法，修改了TSVD，用有限数据进行预测，确定最有效的稳定策略；Ivanov等［5］研究了两类SEIR模型，一类由常微分方程组描述，另一类以一阶差分方程的离散模型描述，预测了疫情的高峰日和最大感染人数；Bentout等［6］运用SEIR模型对阿尔及利亚进行预测，利用最小二乘法和最小化残差平方和的方法拟合数据，估计了流行病相关参数和基本繁殖数；蔡洁等［7］考虑了新冠肺炎疫情期间城市的管控力度，基于SEIR模型模拟出武汉市疫情发展情况；许家雪等［8］在传统SEIR传染病模型基础上，结合实际情况建立疫情传播的微分方程，并对疫情的传播规模进行了预测。以上文献表明，SEIR模型能够清晰地描述出病毒传播的逻辑关系，并能对疫情的发展趋势进行较为准确的预测。但是传统的SEIR模型没有综合考虑疫情地区人口流动、感染人员可能死亡、潜伏时滞可能是时变的等重要的影响因素。

综上所述，本文对传统的SEIR模型进行了改进，给出了SEIR非线性时变时滞模型，所提模型综合考虑了疫情区域人员流动、感染者可能死亡、潜伏时变时滞等不确定因素。因此，可以更精确有效地处理现实问题。对于疫情区域人员流动以及感染人员死亡等影响因素，本文采用混合型高斯混合模型进行建模。根据Expectation-Maximization（EM）算法，确定模型中未知参数的最优取值。最后，以中国湖北省疫情数据对改进后模型进行仿真，且与元胞自动机模型进行了比较。结果表明，本文所提供的模型在运行时间和预测准确性等方面明显优于传统SEIR模型和元胞自动机模型［9］-［11］。

1 前言

为了便于后面进一步分析，本部分对传统的SEIR传染病模型进行了简单的描述，然后给出基本假设。

1.1 传统SEIR模型的描述

传统的SEIR传染病模型如下：

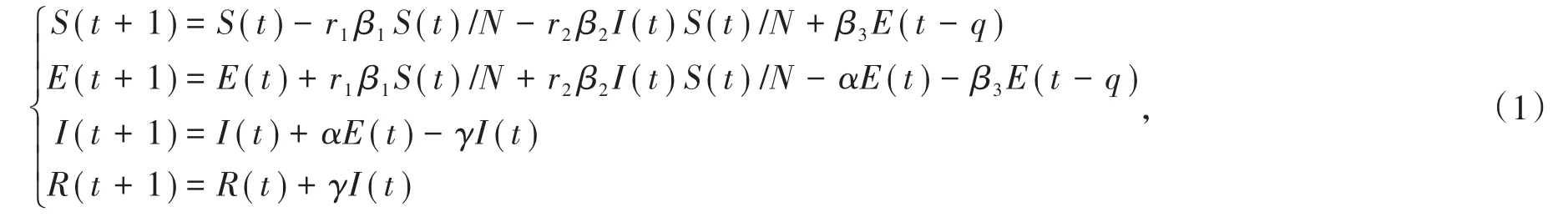
其中，S(t)，E(t)，I(t)和R(t)分别表示易感者，潜伏者，感染者和康复者在t时刻的人数；q是常数，表示潜伏期的时间；α表示潜伏者转为感染者的概率；γ表示感染者康复的概率；r1表示每个感染者平均每天接触的人数；r2表示每个潜伏者平均每天接触人数；β1表示患者的传染概率；β2表示潜伏者传染概率；β3表示新冠肺炎患者转阴率;N表示疫情地区总人数。

模型（1）反映的传染病传播路径的示意图如图1表示：

图1 传统的SEIR传染病模型的示意图

注1：从模型（1）和图1可以看出，传统的SEIR传染病模型没有考虑到疫情地区人员流动和死亡等因素的影响。实际中，疫情地区人员的流动以及受疫情感染人员的死亡对疫情的防控以及疫情的发展预测有着极大的影响。为了使传统模型（1）能更好的解决实际问题，本文在原有模型的基础上增加了人员流动和死亡两个重要的影响因素。

注2：模型（1）中考虑的潜伏时间仅为常数，而在实际中，潜伏时间可能因人而异，甚至是未知时变的。本文将研究将潜伏时滞为常数推广到时变的情况。

1.2 基本假设

假设1：假设新型冠状肺炎只存在人传人的现象。

假设2：不考虑外界环境因素对病死率参数的影响。

假设3：假设感染者康复后自身携带抗体，不会再出现二次感染的情况。

假设4：假设未被发现的病毒携带者和其他人接触的机会相等。

注3：因截至目前，只发现人传人现象，所以假设1是合理的；因目前还未发现外界环境因素如空气质量、温度、湿度等对疫情的传播及感染有重要影响，所以假设2是合理的；因至今还未出现感染者康复后二次感染的情况，所以假设3是合理的；在未加有效控制的情况下，人们生活正常，人与人接触机会相等，因此假设4是合理的。

2 模型建立

2.1 对于传统模型的改进

本部分内容我们对模型（1）进行改进。为了更加深入地研究各种因素对新冠病毒感染性的影响，在传统的SEIR模型的基础上，我们增加了城市人口迁入与迁出等变量。因为对疫情采取了防控隔离措施，并且康复者具有抗体，不考虑再次被感染的情况，故本文在传统的SEIR模型中增加了康复者、外界人口、死亡人员这三个群体。

改进后的SEIR传染病模型为：

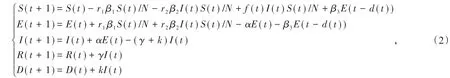
其中，k表示死亡率；d(t)为潜伏时变时滞；疫情地区人员流动情况用以下的高斯混合模型来描述：

其中，ai,bi,ci为可调参数，在文中后面部分将会给出确定其最优值的方法。

模型（2）的示意图如图2所示：

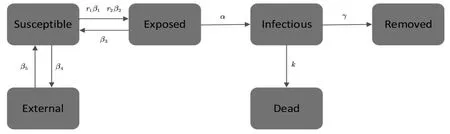
图2 改进的SEIR传染病模型

其中β5表示迁入率，β4表示迁出率，它们的差值β4-β5可用高斯型函数（3）进行模拟。

注4：与模型（1）相比，模型（2）加入感染人员死亡以及外界人口迁入迁出等因素，当参数β4、β5以及k极小时，模型（2）退化为模型（1），因此模型（1）是模型（2）的一个特例。从数学角度看，f(t)是非线性函数，所以模型（1）的简单线性叠加不可能获得模型（2）。

注5：f(t)采用的函数为高斯型混合函数，其中部分参数的最优解可以通过3.2给出的最大期望算法来获得。

2.2 参数的优化与选取

高斯混合模型（Gaussian Mixed Model）指的是多个高斯分布函数的线性组合。主要应用于聚类分析以及概率密度估计上，具有对离散型数据拟合精度高且适用性强的优点。适当的选取GMM中的可调参数，可以很好地描述疫情地区人员流动的情况。下面给出GMM中可调参数的具体优化方法。

GMM模型的EM优化原理［11］：GMM（Gaussian Mixture Model）高斯混合模型由K个Gaussian分布组成，每个Gaussian称为一个“高斯分量”，这些高斯分量的线性组合就组成了GMM的概率密度函数：

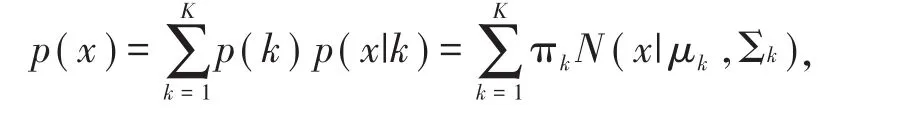
其中πk表示每个高斯分量被选中的概率（权值），μk表示均值，Σk表示方差。

GMM的对数似然函数为：

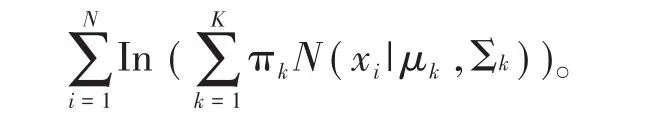
由于对数函数里面有加权，无法用直接求导的方法求解该方程的求最大值。为了解决这个问题，我们采取EM算法进行优化参数，下面给出算法的具体步骤：

步骤1：估计数据由每个高斯分量生成的概率（并不是每个高斯分量被选中的概率）;对于每个数据来说，它的第k个高斯分量生成的概率为

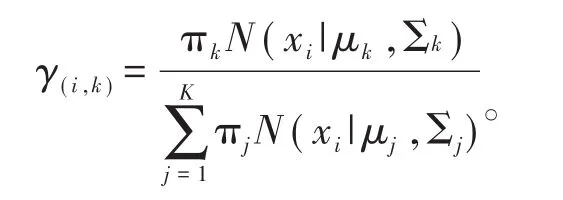
步骤2：估计每个高斯分量的参数：假设上一步得到的 是正确的“数据x由高斯分量k生成的概率”，亦可当作该高斯分量在生成这个数据上所做的贡献。集中考虑所有的数据点，实际上可以看作高斯分量生成了γ(1,k)x1,……,γ(N,k)xN这些点。由于每个高斯分量都是一个标准的Gaussian分布，可以容易求出最大似然所对应的参数值如下：

步骤3：重复迭代前两步，直到似然函数的值收敛为止。

算法检验：采用以上算法得出GMM中项数n选为3是效果最好，即：

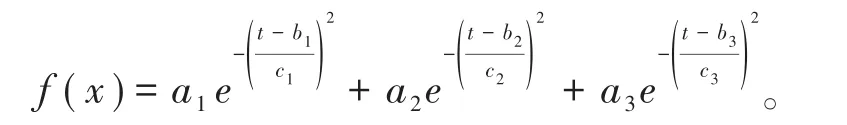
其中利用MATLAB编程得到的部分数据如表1所示：

表1 各个参数的选取以及其置信区间

结果显示错误平方和为SSE=9.117，多重测定系数R-square=0.8984，表明该函数对此数据具有较好的拟合效果，拟合图如图3所示：

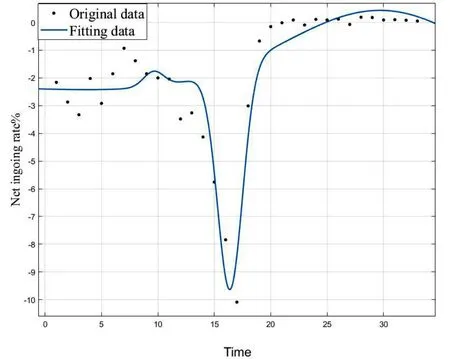
图3 函数拟合图

对于易感者引入了人口流动以β3-β4表示人口净迁入率，潜伏周期q=d(t)，对模型（2）进行优化得：

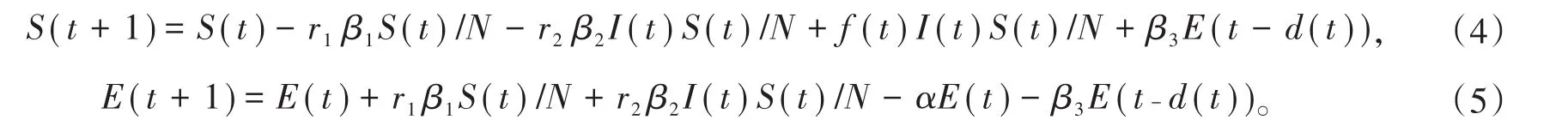
感染者以k的概率死亡，引入死亡者人数的变化方程：

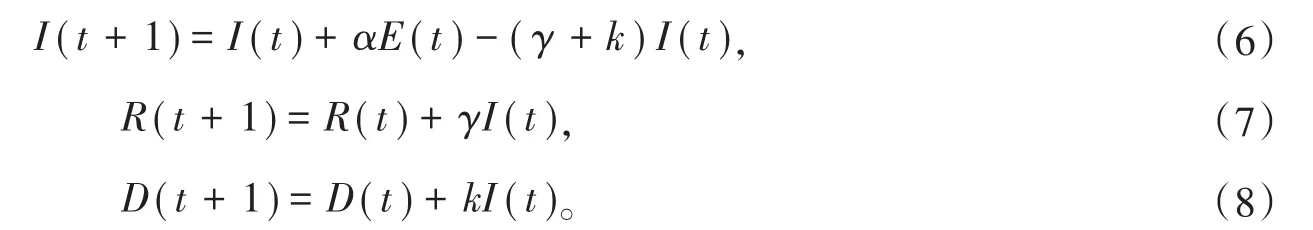
由上可知，改进后的SEIR传染病模型为：

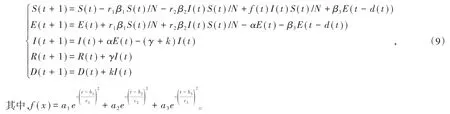
注6：如果所给数据不同，参数优化的结果也会不同。

3 仿真研究

3.1 改进模型数据仿真

为了说明所提模型的有效性，以下以中国湖北省为例。根据相关文献以及中国卫健委发布的每日湖北省新冠肺炎新增人数、治愈人数以及湖北省人口迁移等相关数据，可选择参数如下：β1=0.6，β2=0.125，β3=0.11，α=0.07，r1=10，r2=20，k=0.037，γ=0.0601.

部分统计数据如表2所示：

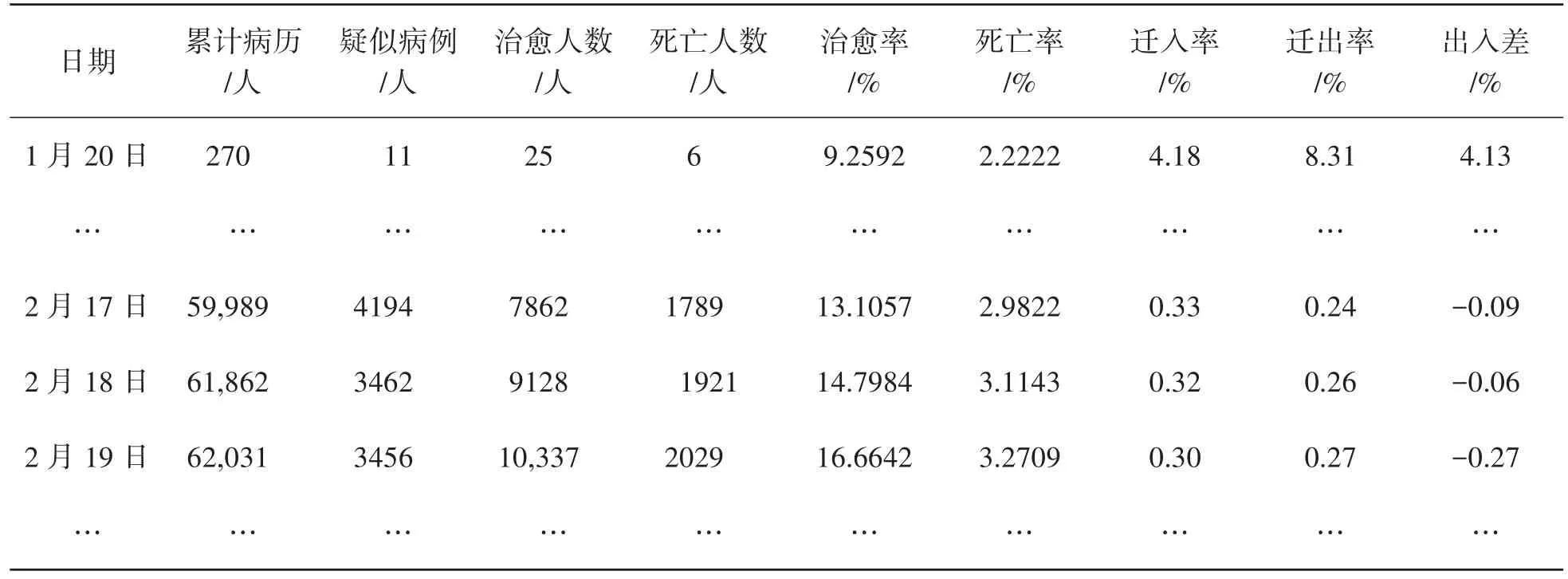
表2 湖北省新冠肺炎2020年1月20日—2月19日疫情统计数据

将以上参数代入模型（2）中，得到的结果如图4所示，其中潜伏时间q=7，由参数r1r2反映隔离强度，取不同的r1r2所得到的结果如图4和图5所示，结果可知不同隔离强度下疫情得以控制的程度不同，在较高水平隔离措施下，患者及潜伏者人数远远小于在较低水平隔离措施下患者及潜伏者的人数。因此，采取封城、限制居民出去、各类隔离手段是相当有必要的，可以很大程度上缓解疫情往坏的方向发展的趋势。在采取高水平隔离措施的条件下，疫情暴发后15天左右新冠肺炎感染者人数达到一个峰值，约为8.5万人，疫情暴发后四个月左右基本稳定，得以控制；而在较低水平隔离措施条件下，感染人数的峰值将达到13.8万人。考虑时变时滞，这里取d(t)=7+(-1)t，在较高水平隔离措施的前提下，它的峰值将达到7.5万人，结果如图6所示。截至目前，湖北的累计感染人数为6.8万人，说明考虑时变时滞时，本文所用的方法同样适用，并且更符合实际，如果能给出更为精确的时变时滞，那么预测结果将会更加准确。

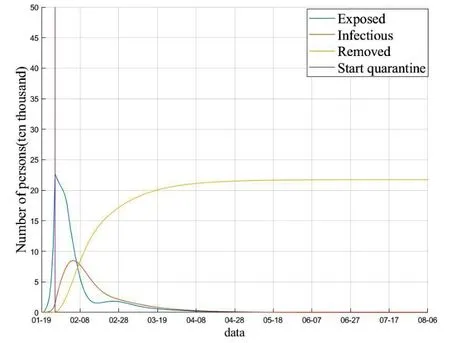
图4 r1=10，r2=20时各类人群人数预测图

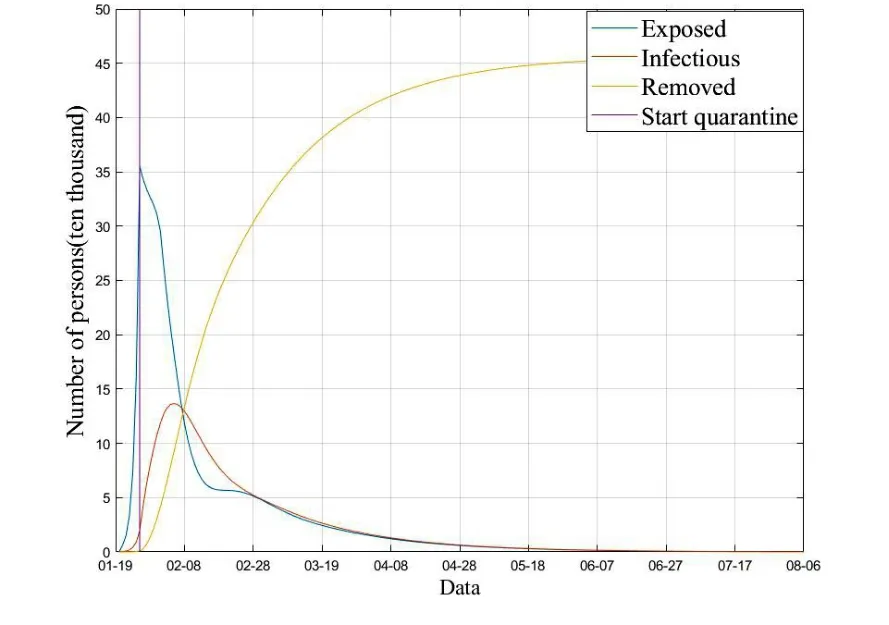
图5 r1=20，r2=30时各类人群人数预测图

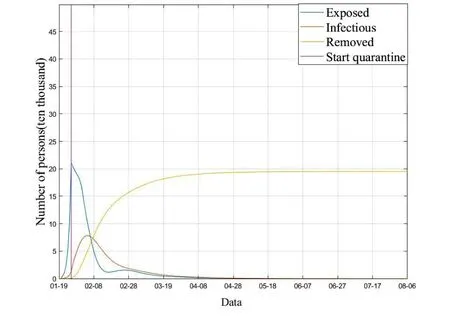
图6 加入时变时滞后各类人群人数预测图

3.2 与元胞自动机模型比较

用文献［9］［12］提供的元胞自动机模型进行仿真，参数选取与3.1所述相同，可得结果如图7所示：

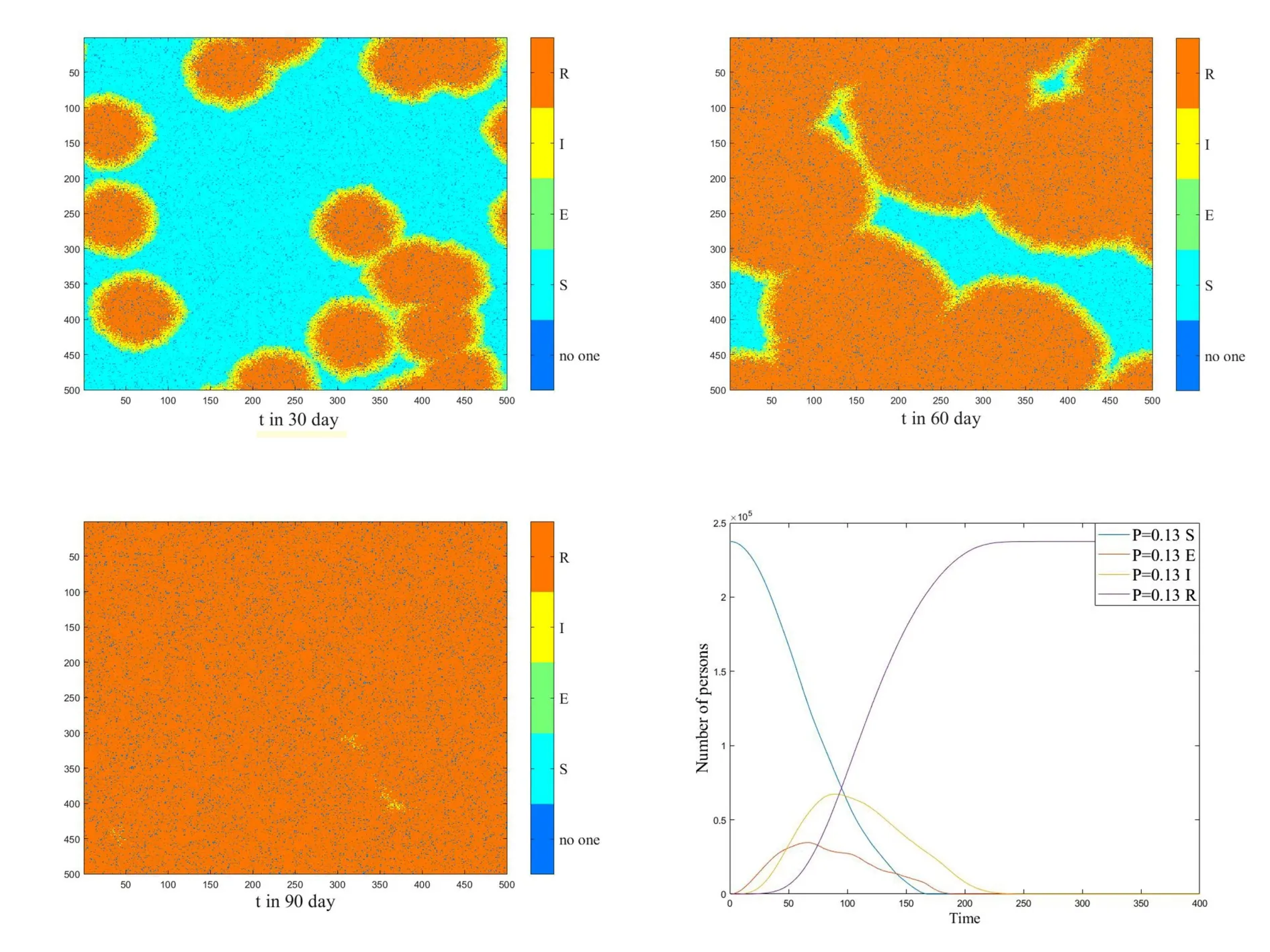
图7 湖北省新冠肺炎疫情元胞自动机空间模拟结果示意图及四种人群随时间变化结果图

从图6和图7数据仿真结果与疫情实际发展数据对比来看，文中所提供的方法，在模型的精确度以及使用范围等方面明显优于传统的SEIR模型以及元胞自动机模型［13-14］。改进后的SEIR传染病模型具有运行时间短，参数易获取，模型简单易行且预测结果更精确等特点。当考虑人口流动以及隔离状态不稳定时，元胞自动机模型无效或不再适用，而本文方法仍能适用。

4 结论

本文就传统的SEIR模型进行改进，以湖北省疫情发展的参数对其进行仿真，并将得到的结果与元胞自动机模型仿真出来的结果进行比较。可以发现，改进后的SEIR模型可以更好地预测新冠肺炎疫情发展趋势，且可通过对参数的控制提出疫情防控方面的举措，对做好精准防控具有很好的指导作用，可以将改进后的新的新型冠状肺炎SEIR传染病模型推广到其他仍存在疫情的国家，帮助他们更有效地做好疫情防控工作，这也是我们后续研究的方向。